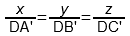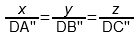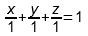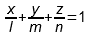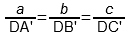Как строить треугольник гиббса розебома (3 видео)

Как строить треугольник гиббса розебома

На третьем курсе на занятиях по физической химии мы изучали различные диаграммы состояния. Особо запомнились своим довольно необычным видом такие диаграммы при постоянных температуре и давлении для систем, состоящих из трёх веществ, так как изображались они в виде равностороннего треугольника (т. н. «треугольник Гиббса-Розебома»), где каждая его точка соответствовала смеси какого-либо определённого состава (рис. 1, 2), а концентрации выражались как доли компонентов.

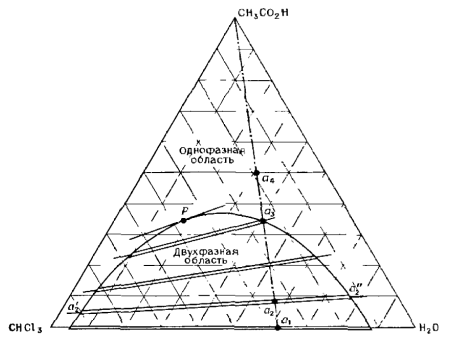
Рис. 1. Трёхкомпонентная система уксусная кислота – хлороформ – вода при комнатной температуре [1, с. 338].

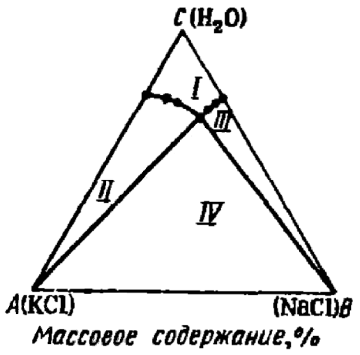
Рис. 2. Диаграмма растворимости KCl и NaCl в воде при 298 К [2, с. 485].

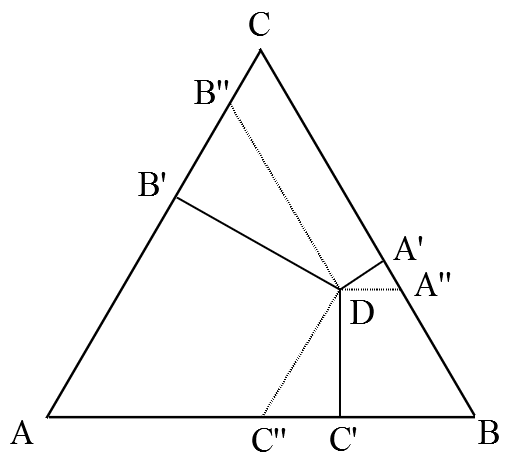
Также на лекциях нам рассказывали про два правила, по одному из которых каждой точке треугольника-диаграммы ставился в соответствие состав трёхкомпонентной смеси. Опишу кратко эти правила [3, с. 229] на примере системы из веществ A, B и C, мольные доли которых составляют x , y и z соответственно. Рассмотрим точку D внутри равностороннего треугольника △ABC (рис. 3). Какому соотношению x : y : z она соответствует?

Рис. 3. Определение состава смеси по правилам Гиббса и Розебома.

1) По правилу Гиббса высота треугольника принимается за единицу (или за 100%) и используется тот факт, что сумма длин перпендикуляров, опущенных из точки D на стороны треугольника равна его высоте. В этом случае концентрации (доли) компонентов пропорциональны длинам этих перпендикуляров:

x : y : z = DA’ : DB’ : DC’

2) По правилу Розебома за единицу (за 100%) принимается длина стороны треугольника, при этом из точки D проводятся отрезки, параллельные каждой из его сторон (на рис. 3 это DA», DB», DC»). Сумма их длин равна стороне треугольника и выполняется следующее соотношение:

x : y : z = DA» : DB» : DC»

или в иной записи

Легко видеть, что правила Гиббса и Розебома нисколько не противоречат друг другу:

x : y : z = DA’ : DB’ : DC’ = DA» : DB» : DC»

Это обусловлено тем, что △DA’A», △DB’B» и △DC’C» являются подобными (как треугольники с равными углами: ∠DA’A» = ∠DB’B» = ∠DC’C» = 90°; а ∠DA»A’ = ∠DB»B’ = ∠DC»C’ = 60°, поскольку DA» || AB, DB» || BC, DC» || AC).

Простого запоминания описанных правил вполне хватило для подготовки к сдаче экзамена, тем более дальнейшая жизнь сложилась так, что за все последующие годы с диаграммами состояния мне иметь дело особо-то и не доводилось. Тем не менее в те времена появилось ощущение, что что-то в этих правилах определения состава системы меня смущает и спустя год я понял, что же именно. Дело было в следующем. Очевидно, что доли компонентов системы связаны между собой соотношением

однако из такого равенства неизбежно следует, что для графического изображения множества точек, координаты которых удовлетворяют такому равенству, необходимо использовать трёхмерное пространство, потому что переменных в уравнении три, но при этом треугольник Гиббса-Розебома – это именно треугольник, то есть плоская (двумерная) фигура. Почему так? В итоге до меня дошла очень простая вещь: если переписать (3) как

то получается известное из аналитической геометрии «уравнение плоскости в отрезках», которое в общем виде записывается так:

где l , m и n – точки, в которых данная плоскость пересекает оси абсцисс, ординат и аппликат соответственно. Отсюда получается, что треугольник Гиббса-Розебома располагается именно в плоскости, описываемой уравнением (4). Можно сказать иначе: поскольку каждая из величин x , y , z принимает значения от 0 до 1 (потому что это доли компонентов в смеси), то треугольник Гиббса-Розебома является расположенным в первом октанте графиком функции

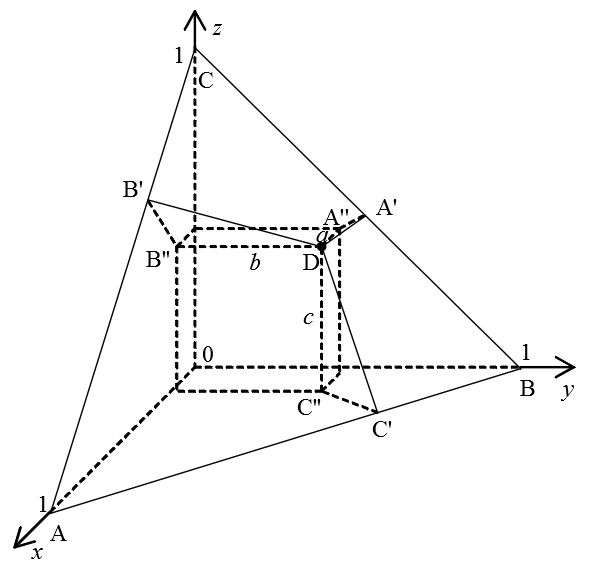
Из этого факта как раз и следует, что для построения диаграммы состояния трёхкомпонентной системы вполне достаточно плоского изображения. А ещё любопытно здесь другое. Взгляните на рис. 4 – на нём изображён треугольник Гиббса-Розебома в «трёхмерном» представлении.

Рис. 4. Треугольник Гиббса-Розебома, представленный как график функции z = 1 – x – y .

В △ABC выбрана точка D, от которой к сторонам этого треугольника проведены перпендикуляры DA’, DB’, DC’. Сама точка D имеет координаты ( a , b , c ), численные значения которых являются концентрациями входящих в состав смеси компонентов. Вершины △ABC с точкой начала координат образуют тетраэдр и из симметрии данного геометрического тела следует, что двугранные углы, образованные плоскостью △ABC и координатными плоскостями, равны. При этом в соответствии с теоремой, обратной теореме о трёх перпендикулярах , получается, что A’A» ⊥ BC, B’B» ⊥ AC, C’C» ⊥ AB, следовательно ∠DA’A», ∠DB’B» и ∠DC’C» являются линейными углами соответствующих двугранных углов, и значит они равны между собой. Отсюда вытекает, что △DA’A», △DB’B» и △DC’C» – подобные, из чего напрямую получается соотношение для правила Гиббса, аналогичное (1):

В связи с этим мне в голову уже давно закралась следующая мысль: а может создатели диаграмм состояния, когда разрабатывали способы наглядного преставления характеристик трёхкомпонентых систем, руководствовались схожими соображениями – про уравнение плоскости «в отрезках», про получающиеся при этом подобные треугольники и т. д.? Не удивлюсь, если такое действительно было опубликовано тем же самым Дж.У. Гиббсом в своих научных работах, а теперь, спустя более века и став классикой, успело подзабыться. В учебниках по физической химии, на которые я выше ссылался, и в ряде других [5, с. 422; ; 7, с. 401], сведений, подтверждающих приведённые догадки, нет – такую информацию нужно искать специально, но сначала необходимо суметь заставить себя заняться подобными поисками.

Кстати, схожая ситуация наблюдается и в отношении «правила креста» – очень легко отыскать литературу и сайты, где подробно рассказывается как решать задачи на смешение растворов с использованием этого правила, а вот материала, в котором описано откуда именно это правило берётся (то есть его математическое обоснование), мне обнаружить не удалось – пришлось восполнять этот пробел самостоятельно написанием соответствующей заметки.

Эткинс П. Физическая химия. Том 1. М.: Мир, 1980. – 586 с.
Физическая химия. В 2 кн. Кн. 1. Строение вещества. Термодинамика. Учеб. для вузов / Под ред. К.С. Краснова – 3-е изд., испр. – М.: Высшая школа, 2001. – 512 с.
Карякин Н.В. Основы химической термодинамики: Учеб. пособие для вузов. Нижний Новгород: Издательство ННГУ им. Н.И. Лобачевского; М.: Издательский центр «Академия», 2003. – 464 с.
Геометрия: Учеб. для 10-11 кл. сред. шк. / Л.С. Аганасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 1992. – 207 с.
Курс физической химии, том 1 / Под ред. Я.И. Герасимова. М.: Химия. 1964. – 624 с.
Карапетьянц М.Х. Химическая термодинамика: Учебное пособие. Изд. 4-е. М.: Книжный дом «ЛИБРОКОМ», 2013. – 584 с.
Киреев В.А. Курс физической химии. Изд. 3-е, перераб. и доп. М.: Химия, 1976. – 775 с.

Видео:Треугольник Гиббса. 2 часть. Задача. Метод РозебомаСкачать

Метод Гиббса и Розебома.

Фазовые диаграммы трехкомпонентных систем.

Добавление третьего компонента к бинарной системе всегда влияет на взаимную растворимость данных двух компонентов. При этом критическая температура бинарной системы может возрастать или уменьшаться, т.е. взаимная растворимость первых двух компонентов может улучшаться или ухудшаться. Это зависит от способности третьего компонента растворяться в первых двух. Допустим , что компоненты А и Б ограниченно смешиваются. Если третий компонент С в равной степени растворим в компонентах А и Б, то взаимная смешиваемость компонентов А и Б улучшается., ВКТР понижается и НКТР повышается. Если третий компонент растворим в компоненте А значительно лучше чем в компоненте Б (или наоборот), то взаимная растворимость А и Б ухудшается, ВКТР повышается, а НКТР понижается. Проиллюстрируем это следующим примером. Система фенол-вода обладает ВКТР, равной 338К. Добавление 1% нафталина, который растворяется в феноле и не растворяется воде, приводит к повышению ВКТР до 353 К; добавление 1% олеата натрия, хорошо растворимого и в воде и в феноле, понижает T_c до 316К.

Аналогичная картина наблюдается при добавлении неорганических солей и кислот к двум ограниченно смешивающимся жидкостям А и Б. Если электролит хорошо растворим в обеих жидкостях, то при его добавлении их взаимная растворимость улучшается; если только в одной из них — то ухудшается. Так, электролиты NaCl, KCl, MgSO₄ и др., хорошо растворимые в воде и не растворимые в феноле, вызывают сильное повышение критической температуры и искажение бинодали, связанное с тем, что система уже не является строго бинарной. При большом количестве добавленного электролита, не растворимого в одном из компонентов бинарной смеси, может произойти ее расслоение даже в том случае, если компоненты полностью смешивались. Это явление получило название высаливания. Если электролит растворим в обеих ограниченно смешивающихся жидкостях, то его добавление вызывает улучшение их взаимной растворимости, что обозначается термином
всаливание.

Явление высаливания очень подробно изучено для водных растворов белков, а для низкомолекулярных жидкостей имеющиеся в литературе данные были обобщены Блешинским, который трехкомпонентные системы жидкость-жидкость-электролит представил в виде диаграмм, одной осью которых является концентрация электролита (рис. 1). Из рисунка следует возможность различных случаев:

Две жидкости при данной температуре смешиваются неограниченно. Добавление электролита вызывает высаливание и расслаивание системы (рис. 1а).

Две жидкости при данной температуре смешиваются ограниченно, добавление электролита улучшает их взаимное смешение, и при некотором количестве добавленного электролита жидкости начинают смешиваться неограниченно (всаливание) (рис. 1б).

Добавление первых количеств электролита может вызвать улучшение взаимной растворимости жидкостей. (рис 1в) или ухудшение (рис 1г).

Фазовые диаграммы трехкомпонентных систем при постоянной температуре обычно выражают в виде равностороннего треугольника, вершины которого отвечают 100% каждого компонента, а точки, лежащие на его сторонах — составам бинарных систем. Любая точка, лежащая внутри треугольника, отражает состав трехкомпонентной системы. Для построение таких диаграмм требуется любым методом определить состав трехкомпонентной системы, при котором она расслаивается. Часто для этой цели используют метод точек помутнения, т.е. при заданной температуре фиксируют количество третьего компонента, вызывающего помутнение бинарной смеси заданного состава. Затем строят диаграмму по методам Розебома или Гиббса.

Метод Гиббса и Розебома.

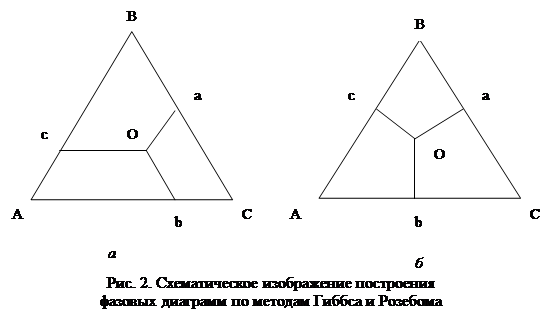В методе Розебома за единицу принимается сторона равностороннего треугольника, на который откладывают мольные доли трех компонентов в расслаивающейся системе (рис. 2а). Через точки M и N проводят линии параллельные сторонам треугольника до пересечения их в точке О. Отрезок Оа, т.е. линия, соединяющая точку О со стороной, лежащей против угла А, отвечающего 100% данного компонента, равна его содержанию в трехкомпонентном растворе. Аналогично этому, отрезок Оb отвечает содержанию компонента Б и отрезок Ос — содержанию компонента С.

В методе Гиббса за единицу принимается высота треугольника и состав смеси выражают линиями, перпендикулярными сторонам треугольника, соединяющими точки внутри его со сторонами, лежащими против углов, отвечающих 100% данного компонента (рис. 2б).

Видео:Метод РозебомаСкачать

ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ. Практикум по химической термодинамике учебное пособие для студентов всех специальностей

Название	Практикум по химической термодинамике учебное пособие для студентов всех специальностей
Анкор	ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ.doc
Дата	19.05.2017
Размер	2.28 Mb.
Формат файла
Имя файла	ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ХИМ ТЕРМОДИНамиКЕ.doc
Тип	Практикум #7896
страница	10 из 15

Подборка по базе: «КЕЙС-СТАДИ» ПРАКТИКУМЫ ТҮРІНДЕГІ.pdf, Математикадан есеп шығару практикумы.docx, Лабораторный практикум.doc, психологический практикум.docx, Технологии искусственного интеллекта Учебно-методическое пособие, Элементы химической термодинамики. Растворы.Растворимость вещест, ПРИЛОЖЕНИЕ4 практикум.doc, Новое пособие по WORD. Лабораторный практикум Часть 2.doc, Зертхана практикум (1).pdf, Лабораторный практикум MS WORD.pdf

Трехкомпонентные системы
Для трехкомпонентной системы, на равновесие которой из внешних факторов оказывают влияние только давление и температура – правило фаз Гиббса –выражается уравнением

С = 5 – Ф.

(3.18)

Отсюда следует, что в трехкомпонентной системе число фаз, находящихся в равновесии, не может быть более пяти (С = 0, если Ф = 5), а максимальное число термодинамических степеней свободы, т.е. независимых параметров состояния системы, равно четырем – давление, температура, концентрации Х₁ и Х₂ двух компонентов, выраженные в массовых или молярных долях или процентах (С = 4, если Ф = 1). При выбранных параметрах состояния системы (Р, Т, Х₁, Х₂) полная диаграмма состояния должна быть четырехмерной. В связи с этим состояние трехкомпонентной системы и равновесие фаз в ней рассматривают при постоянном давлении и строят трехмерную пространственную диаграмму состояния в виде прямой трехгранной призмы, основанием которой служит равносторонний треугольник состава, а по высоте откладывается температура. При Р = const

С_усл = 4 – Ф.

(3.19)

Изучение равновесий в трехкомпонентной системе еще более упрощается при постоянных давлении и температуре. В этом случае, можно использовать плоскую диаграмму состояния, являющуюся сечением трехгранной призмы, параллельным основанию (диаграмма состава). При Р = const и Т = const

С_усл = 3 – Ф.

(3.20)

Для графического изображения состава трехкомпонентных систем при постоянных Р и Т применяются треугольные и прямоугольные диаграммы. Треугольные диаграммы строят по методу Гиббса или по методу Розебома. В каждом из этих методов используется равносторонний треугольник, вершины которого соответствуют чистым компонентам А, В и С (рис. 3.15).

Фигуративная точка, лежащая на любой из сторон треугольника, изображает состав соответствующей двухкомпонентной системы, а фигуративная точка, находящаяся внутри этого треугольника, – состав трехкомпонентной системы. При анализе треугольных диаграмм используют свойства равностороннего треугольника:

1) сумма длин перпендикуляров, опущенных из любой точки, лежащей внутри равностороннего треугольника, на его стороны, есть величина постоянная, равная высоте этого треугольника (KD + КЕ + KF = ВН);

2) сумма отрезков прямых, проведенных параллельно сторонам равностороннего треугольника через любую точку, лежащую внутри этого треугольника, есть величина постоянная, равная стороне треугольника (MN + МО + МР = АВ = ВС = АС).

Из этих свойств следует:

а)точки,лежащие на прямой(LS), параллельной одной из сторон равностороннего треугольника (АС), противолежащей данной вершине (В), изображают составы системы с постоянным содержанием того компонента, которому соответствует эта вершина (В);

б) точки, лежащие на прямой (BG), проходящей через вершину треугольника (В), изображают составы системы с постоянным соотношением концентраций двух других компонентов (А и С).

Метод Гиббса основан на использовании первого свойстваравностороннего треугольника. Для удобства изображения состава трехкомпонентной системы по методу Гиббса каждую высоту треугольника делят на 100 (или 10) равных частей и через точки деления проводят прямые, параллельные сторонам треугольника. Длина каждой полученной части будет соответствовать 1 % (или 10 %). Чтобы по методу Гиббса указать состав трехкомпонентной системы, изображенной на диаграмме фигуративной точкой К (рис. 14), из точки К опускают перпендикуляры на стороны треугольника. Длина каждого перпендикуляра будет отвечать содержанию одного из компонентов: процентное содержание компонента А характеризуется отрезком KF, компонента В – отрезком КЕ и компонента С – отрезком KD.

Метод Розебома основан на использовании второго свойстваравностороннего треугольника. Для удобства изображения состава трехкомпонентной системы по методу Розебома каждую сторону треугольника делят на 100 (или 10) равных частей и через точки деления проводят прямые, параллельные сторонам треугольника. Длина каждой части соответствует 1 % (или 10 %). Для того чтобы по методу Розебома указать состав трехкомпонентной системы, изображенной на диаграмме фигуративной точкой М (рис. 14), из точки М проводят прямые, параллельные сторонам треугольника. Содержание компонента А характеризуется отрезком МР, компонента В –отрезком МО и компонента С –отрезком МN.

Состав трехкомпонентной системы можно также изобразить с помощью прямоугольной диаграммы. Этот способ выражения состава трехкомпонентной системы широко используется при изучении равновесий в растворах солей, имеющих низкую растворимость. Начало координат прямоугольной диаграммы соответствует воде, а концентрации двух солей, наносятся на оси абсцисс и ординат. Этот способ изображения состава значительно проще метода Розебома, но его недостаток в том, что фигуративные точки солей находятся в бесконечности.