Как соответственные элементы равных треугольников

Видео:Признаки равенства треугольников. 7 класс.Скачать

We are checking your browser. mathvox.ru

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6da87267b8f43a8f • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Треугольники. Признаки равенства треугольников

Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .

Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.

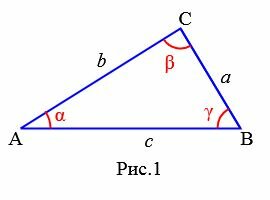Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.

Углы треугольника обозначают так ∠BAC, ∠ABC, ∠BCA. Эти же углы коротко обозначают также ∠A, ∠B, ∠C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.

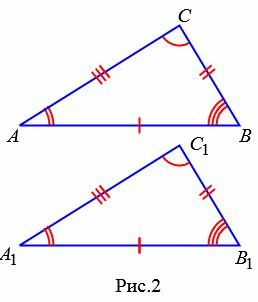
Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A₁B₁C₁. Треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.

Вышеизложенное можно сформулировать так:

Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A₁B₁C₁ обозначается так:

Видео:Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

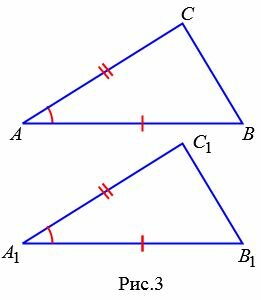Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и ∠A=∠A₁. Докажем, что .

Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Второй признак равенства треугольников

Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

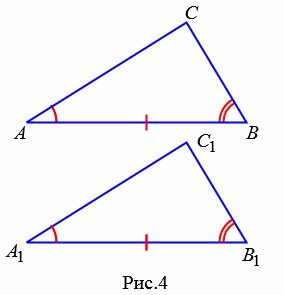Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁ (Рис.4). Пусть AB=A₁B₁, ∠A=∠A₁, ∠B=∠B₁. Докажем, что .

Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

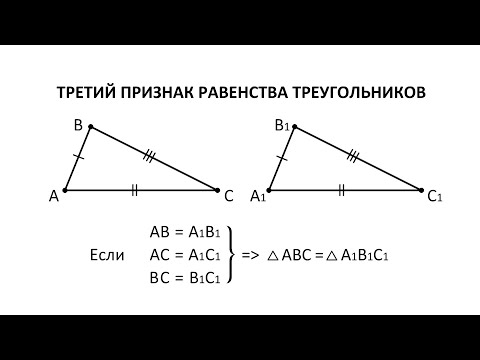
Третий признак равенства треугольников

Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.

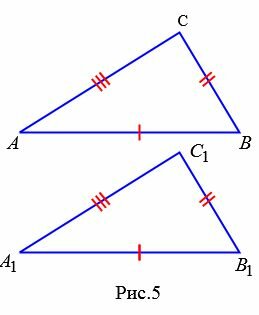Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁. Пусть AB=A₁B₁, AC=A₁C₁ и BC=B₁C₁. Докажем, что . Приложим треугольник ABC к треугольнику A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, вершина B совмещалась с вершиной B₁, а вершины С и С₁ находились по разные стороны от прямой A₁B₁.

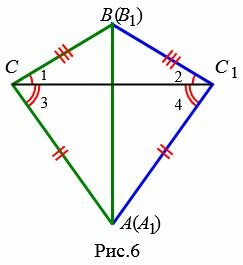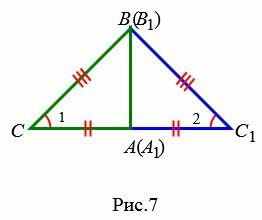
Возможны три варианта: луч CC₁ проходит внутри угла ACB(Рис.6); луч CC₁ совпадает с одной из сторон угла ACB (Рис.7); луч CC₁ проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.

.

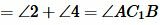Имеем AC=A₁C₁, BC=B₁C₁ ∠ACB=∠A₁C₁B₁ и по первому признаку равенства треугольников . Теорема доказана.

Вариант 2 (Рис.7). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольник BСС₁ равнобедренный. Тогда ∠1=∠2. Имеем: AC=A₁C₁, BC=B₁C₁, ∠1=∠2 и по первому признаку равенства треугольников . Теорема доказана.

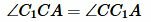
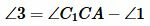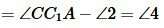Вариант 3 (Рис.8). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и и, следовательно:

.

Имеем AC=A₁C₁, BC=B₁C₁ 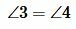и по первому признаку равенства треугольников . Теорема доказана.

Видео:Первый признак равенства треугольников. 7 класс.Скачать

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

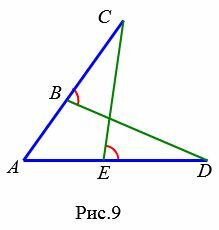Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства .

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

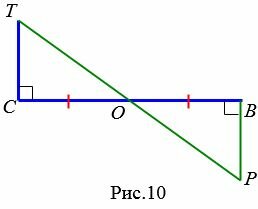Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства .

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Как соответственные элементы равных треугольников

Сроки проведения: 10 декабря 2008 — 15 декабря 2008

1.Возьмем полоску бумаги. Отметим точки A и В. Согнем по прямой АВ.

2. Отметим произвольную точку С и проведем прямую АС.

Получим геометрическую фигуру — треугольник АВС. А, В, С — вершины. АВ, ВС, АС — стороны треугольника. Разогнем полоску в первоначальное положение.

3.Рассмотрим АВС и ABD. Сравним АС и АD и углы, лежащие против этих сторон СВА и DВА. При наложении они совпадают. Аналогично АС и ВD, ВА.

Вывод: в равных треугольниках против равных сторон лежат равные углы, и обратно — против равных углов лежат равные стороны.

(Равные углы и равные стороны в равных треугольниках называются соответственными)

Определите соответственные элементы равных треугольников, полученных с помощью сгибов.

1 способ.

Сделайте намеченный сгиб.	Отметим произвольную точку О и сделайт соответствующие сгибы. Раскройте полоску.
3. Получим два равных треугольника АОВ= СОD (так как совпали при наложении).
Назовите соответственные элементы АВ СD 5= 6 АО ОС 1= 2 ВО ОD 4= 3 (так как они совпадают при наложении)

2 способ.

	Получаем АВС= MNP (так как совпали при наложении).
Назовите соответственные элементы:	NP AB M= C MN BС P= A MP АC N= B

Получаем АВС= MNP (так как совпали при наложении).

Назовите соответственные элементы:

В математике каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы.

Рассмотрите:
1. Два треугольника, у которых равны сторона и два прилежащих к ней угла.
2. Соотношение между сторонами и углами произвольного треугольника.

С помощью сгибов построим два треугольника, у которых равны сторона и два прилежащих к ней угла.

Согните по намеченной линии.	Отметьте точки А и В. Отложите l = 2, 3 = 4 Прямые АМ и ВМ пересекутся в точке М. Прямые AD и BD пересекутся в точке D.
Убедитесь, что точка М и D совпали при наложении. Следовательно, АМВ= АВD

Вывод: (формулировка теоремы) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум другим прилежащим к ней углам другого треугольника, то такие треугольники равны.

Возьмите произвольный треугольник, с помощью сгибов сравните его стороны, и отметьте большую.

1. Сравните АВ и ВС.	2. ВС — часть АВ, следовательно, АВ > ВС. Выберите большую и сравните со следующей стороной.
3. Сравните АВ и АС.	4. А В — часть АС, следовательно, АС >АВ.

АС — большая сторона. ВС — меньшая сторона.

Сравните углы АВС

🔍 Видео

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Второй признак равенства треугольников. 7 класс.Скачать

Высота, биссектриса, медиана. 7 класс.Скачать

Геометрия 7 класс (Урок№14 - Второй и третий признаки равенства треугольников.)Скачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

№128. Докажите, что в равных треугольСкачать

ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

Геометрия. 7 класс. Теоремы. Т8. Третий признак равенства треугольников.Скачать

7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать

3 признак равенства ТРЕУГОЛЬНИКА!Скачать

Третий признак равенства треугольников | Теорема + доказательствоСкачать