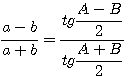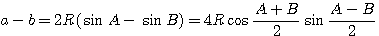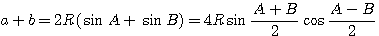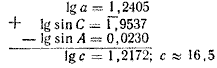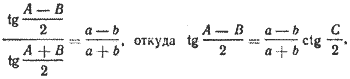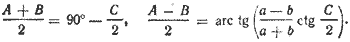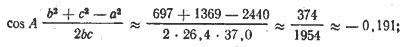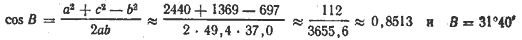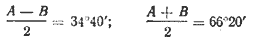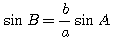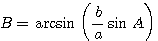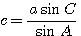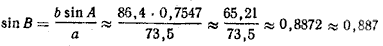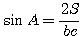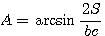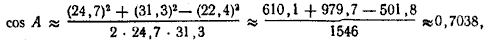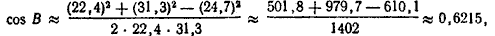Как решать косоугольные треугольники (2 видео)

Как решать косоугольные треугольники

Г л а в а П. Решение косоугольных треугольников

§7(41). Теорема тангенсов

Теорема. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:

(и две аналогичные формулы для прочих пар сторон а, с и b, с).

Доказательство. В силу теоремы синусов имеем:

Разделив почленно эти равенства, получим доказываемую формулу.

§8(42). Решение треугольника по двум его углам и стороне

Задача. Даны два угла треугольника и сторона, прилежащая к ним; вычислить другие стороны и угол.
Даны В, С и а; требуется найти b, с и А.

Решение. Условие возможности построения треугольника по этим данным:
А + В 1 /_0,9483 ≈ 1,055.

Вычисления выполнены по правилам приближённых вычислений. Значения синусов взяты из таблиц Брадиса; во всех промежуточных результатах сохраняются четыре значащие цифры (правило запасной цифры), а окончательный результат округлён до трёх значащих цифр.

Решение при помощи логарифмических таблиц. Имеем:

b = a sin B /_{sin A}, lg b = lg a + lg sin В — lg sin A.

По таблицам найдем:

По таблицам Брадиса найдём b = 12,86. Однако в ответе следует оставить три значащие цифры, так как значение а дано с тремя значащими цифрами; поэтому b ≈ 12,9.

Сторона с вычисляется аналогично:

c = a sin C /_{sin A}, lg c = lg a + lg sin C — lg sin A.

§9(43). Решение треугольника по двум сторонам и углу между ними

Задача. Даны две стороны треугольника и угол между ними; вычислить третью сторону и два других угла.

Пусть, например, даны а, b и С, требуется вычислить А, В и с.

Решение при помощи натуральных таблиц. Формула косинусов даёт выражение стороны с непосредственно через известные элементы:

с = / а 2 + b 2 — 2ab cos С

Для вычисления А можно также воспользоваться формулой косинусов:

Разность углов A — В можно вычислить, воспользовавшись теоремой тангенсов:

Углы А и В определяются из системы уравнений:

Сторону с можно вычислить по теореме синусов:

Пример. Дано: а ≈ 49,4; b ≈ 26,4; С ≈ 47°20′; найти А, В и с.

Решение при помощи натуральных таблиц. Имеем:

с 2 = а 2 + b 2 — 2ab cos С ≈ 49,4 2 + 26,4 2 — 2 • 49,4 • 26,4 • cos 47°20′

По таблицам квадратов найдём:

а 2 ≈ (49,4) 2 ≈ 2449; b 2 ≈ (26,4) 2 ≈ 697,0

2 • 49,4 • 26,4 • cos 47°20′ ≈ 2 • 49,4 • 2,64 • 0,6778 ≈ 1768.

Следовательно, с 2 ≈ 2440 + 697 — 1768 ≈ 1369. По таблицам квадратных корней
с ≈ 37,0. Далее

А ≈ arc cos (—0,191); угол А — тупой.

Находим дополнительный угол

180° — А ≈ arc cos (0,091) ≈ 79°; А ≈ 180° — 79° = 101°

(с округлением до 10′). Наконец,

Решение при помощи логарифмических таблиц. Вычислим углы A и В.

Из системы уравнений

найдём: A ≈ 101°, В ≈ 31°40′.

§ 10 (44). Решение треугольника по двум сторонам и углу,
противолежащему одной из них

Задача. Даны две стороны треугольника и угол А, лежащей против одной из них; вычислить третью сторону и два остальных угла.

Пусть даны a, b и А; требуется вычислить B, С и с

С л у ч а й 1. а > b, т. е, заданный угол А лежит против большей стороны.

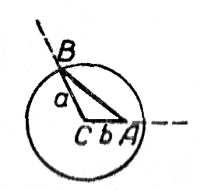
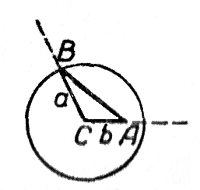
Построение показано на чертеже. Из точки С (как из центра), взятой на одной из сторон угла А на расстоянии b от вершины, описана окружность радиуса а; точка В есть точка пересечения этой окружности с другой стороной угла А.
Построение всегда возможно, задача имеет единственное решение.

Острый угол В, противолежащий меньшей стороне, находится по теореме синусов:

откуда

и затем С = 180° — (A + В). Сторона с находится по теореме синусов:

С л у ч а й 2. а 90° задача не имеет решения.
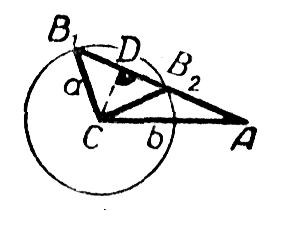
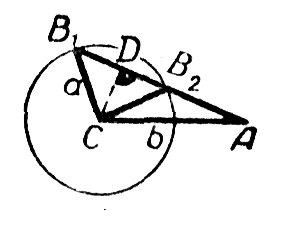
Пусть угол А острый. Из построения на чертеже a) , видно, что окружность радиуса а с центром в точке С пересечёт другую сторону угла А в двух точках при условии а > CD, где D — основание перпендикуляра, опущенного из точки С на другую сторону угла A. Так как CD = b sin A (из треугольника ACD), то условие запишется так: a >b sinA. Для угла В возможны два значения: В = В₁ (острый) и В = В₂ (тупой). Задача имеет два решения.

Значения угла В вычисляются по теореме синусов:

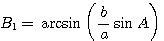
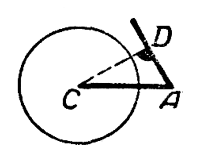
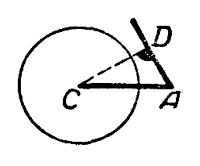
откуда и B₂ = 180° — B₁ Значения угла С и стороны с вычисляются так же, как в предыдущем случае.

Из чертежа b) видно, что при
CD = b sin А > а окружность не пересечёт другой стороны угла А; задача не имеет решений.

В этом случае 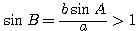и угол В вычислить нельзя.

При CD = b sin А задача имеет единственное решение: треугольник ABC прямоугольный.

Случай 3. а = b. В этом случае треугольник ABC равнобедренный. Такой треугольник можно решить, разбразбив его высотой CD на два прямоугольных треугольника:

В = А; С = 180° — 2А; с = 2AD = 2а cos A.

Пример. Вычислить стороны и углы треугольника, если дано:

(деление на 73,5 можно заменить умножением на 1 /_73,5 ≈ 0,0136, табл. 11).

Так как в данном случае а b sin A /_a а + b, то треугольник с данными сторонами не существует. Будем считать, что с 2 =b 2 + с 2 — 2bc cos А
b 2 =c 2 + a 2 — 2ca cos B, откуда

и (так как 0° / р (р — а)(р — b) (р — с) , где р = (а+ b+c)/2

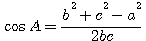
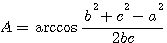
Имеем далее: S = 1 /₂ bc sin A. откуда

Угол А острый, так как он лежит против меньшей стороны; следовательно,

Точно также 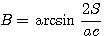и, наконец, С = 180° — (А + В)

Итак, при решении треугольника по трём сторонам при помощи логарифмических таблиц углы, лежащие против меньших сторон, находятся по формулам, а угол, лежащий против наибольшей стороны, вычисляется как разность между 180е и суммой двух найденных углов.

Пример. Решить треугольник, зная длины (приближенные) его сторон: 24,7; 22,4 и 31,3. Обозначим a ≈ 22,4; b ≈ 24,7; с ≈ 31,3.

Решение при помощи натуральных таблиц. Имеем:

откуда А ≈ 45°20′ (с округлением до 10′).

откуда В ≈ 51°30′ и, наконец, С ≈ 180° — (45°20′ + 51°30′) ≈ 83°10′.

Решение при помощи логарифмических таблиц. Имеем:

sin А = 2S /_bc, lg sin А = lg 2S — lg b — lg c.

Решить косоугольные треугольники по заданным основным элементам. (Решение каждого примера следует выполнить при помощи таблиц логарифмов и логарифмической линейки.)

81 (347). Даны сторона и два угла:

1) а ≈ 370,0; В ≈ 86°30′; С ≈ 50°50′

2) а ≈ 450,0; А ≈ 87°50′; В ≈ 10°50′.

3) а ≈ 951; B ≈ 126°40′; С ≈ 13°20′.

4) b ≈ 13,02; A ≈ 11°46′; B ≈ 133°40′.

82 (348). Даны две стороны и угол между ними:

1) а ≈ 510; b ≈ 317; С ≈ 76°10′.

2) а ≈ 225; b ≈ 800; С ≈ 36°40′.

3) а ≈ 2,296; с ≈ 1,687; В ≈ 29°52′.

4) b ≈ 28; c ≈ 42; А ≈ 124°.

83 (349). Даны две стороны и угол против одной из них:

2) b ≈ 360; с ≈ 309; С ≈ 21°30′.

3) а ≈ 13,89; с ≈ 8,42; А ≈ 126°41′.

4) а ≈ 13,81; с ≈ 8,14; С ≈ 14°37′.

5) b ≈ 263,1; с ≈ 215,4; В ≈ 70°14′.

6) а ≈ 19,06; b ≈ 88,19; А ≈ 31°17′.

84 (350). Даны три стороны:

85 (351). Решить косоугольные треугольники по заданным моментам:

1) R ≈ 7,92; А ≈ 113°17′; В ≈ 48°16′.

2) S ≈ 501,9; А ≈ 15°28′; B ≈ 45°23′.

5) а + b ≈ 488,8; А ≈ 70°24′; В ≈ 40°16′.

Содержание

Решение косоугольных треугольников
Решение треугольника по двум его углам и стороне
Решение треугольника по двум сторонам и углу между ними
Решение треугольника по двум сторонам и углу, противолежащему одной из них
Решение треугольников онлайн
Решение треугольника по трем сторонам
Решение треугольника по двум сторонам и углу между ними
Решение треугольника по стороне и любым двум углам
🌟 Видео

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Решение косоугольных треугольников

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Решение треугольника по двум его углам и стороне

Задача. Даны два угла треугольника и сторона, прилежащая к ним; вычислить другие стороны и угол.

Даны В, С и а; требуется найти b, с и А.

Решение. Условие возможности построения треугольника по этим данным:

А + В 1 /_0,9483 ≈ 1,055.

Решение при помощи логарифмических таблиц. Имеем:

b = a sin B /_{sin A}, lg b = lg a + lg sin В — lg sin A.

По таблицам найдем:

lg a = 1,2405, lg sinB = 1,8457, ld sin A = 1,9770, откуда lg b = 1,1092

Сторона с вычисляется аналогично:

c = a sin C /_{sin A}, lg c = lg a + lg sin C — lg sin A.

. lg c = 1,2172; c ≈ 16,5

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Решение треугольника по двум сторонам и углу между ними

Задача. Даны две стороны треугольника и угол между ними; вычислить третью сторону и два других угла.

Пусть, например, даны а, b и С, требуется вычислить А, В и с.

Для вычисления А можно также воспользоваться формулой косинусов:

Разность углов A — В можно вычислить, воспользовавшись теоремой тангенсов:

Углы А и В определяются из системы уравнений:

Сторону с можно вычислить по теореме синусов:

Пример. Дано: а ≈ 49,4; b ≈ 26,4; С ≈ 47°20 найти А, В и с.

Решение при помощи натуральных таблиц. Имеем:

с 2 = а 2 + b 2 — 2ab cos С ≈ 49,4 2 + 26,4 2 — 2 • 49,4 • 26,4 • cos 47°20&#146

По таблицам квадратов найдём:

а 2 ≈ (49,4) 2 ≈ 2449; b 2 ≈ (26,4) 2 ≈ 697,0

2 • 49,4 • 26,4 • cos 47°20&#146 ≈ 2 • 49,4 • 2,64 • 0,6778 ≈ 1768.

Следовательно, с 2 ≈ 2440 + 697 — 1768 ≈ 1369. По таблицам квадратных корней

А ≈ arc cos (-0,191); угол А — тупой.

Находим дополнительный угол

180° — А ≈ arc cos (0,091) ≈ 79°; А ≈ 180° — 79° = 101°

(с округлением до 10&#146). Наконец,

Решение при помощи логарифмических таблиц. Вычислим углы A и В.

$$ lg tgfrac=lg(a-b) + lg ctgfrac — lg(a+b) $$
$$ lg tgfrac=1,8403 ;;и;; fracapprox 34°40&#146 $$

Из системы уравнений

найдём: A ≈ 101°, В ≈ 31°40&#146.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Решение треугольника по двум сторонам и углу, противолежащему одной из них

Пусть даны a, b и А; требуется вычислить B, С и с

С л у ч а й 1. а > b, т. е, заданный угол А лежит против большей стороны.

Острый угол В, противолежащий меньшей стороне, находится по теореме синусов:

и затем С = 180° — (A + В). Сторона с находится по теореме синусов: ( c=frac )

С л у ч а й 2. а 90° задача не имеет решения.
Пусть угол А острый. Из построения на чертеже a), видно, что окружность радиуса а с центром в точке С пересечёт другую сторону угла А в двух точках при условии а > CD, где D — основание перпендикуляра, опущенного из точки С на другую сторону угла A. Так как CD = b sinA (из треугольника ACD), то условие запишется так: a >b sinA.

Для угла В возможны два значения: В = В₁ (острый) и В = В₂ (тупой). Задача имеет два решения.

a) Значения угла В вычисляются по теореме синусов: ( sinB = fracsinA )

Из чертежа видно, что при CD = b sinА > а окружность не пересечёт другой стороны угла А; задача не имеет решений.

При CD = b sin А задача имеет единственное решение: треугольник ABC прямоугольный.

В = А; С = 180° — 2А; с = 2AD = 2а cos A.

Пример. Вычислить стороны и углы треугольника, если дано:

(деление на 73,5 можно заменить умножением на 1 /_73,5 ≈ 0,0136).

Так как в данном случае а b sin A /_a а + b, то треугольник с данными сторонами не существует. Будем считать, что с 2 =b 2 + с 2 — 2bc cos А
b 2 =c 2 + a 2 — 2ca cos B, откуда

Угол А острый, так как он лежит против меньшей стороны; следовательно,

Точно также ( B = arcsinfrac ) и, наконец, С = 180° — (А + В)

Итак, при решении треугольника по трём сторонам при помощи логарифмических таблиц углы, лежащие против меньших сторон, находятся по формулам, а угол, лежащий против наибольшей стороны, вычисляется как разность между 180° и суммой двух найденных углов.

Пример. Решить треугольник, зная длины (приближенные) его сторон: 24,7; 22,4 и 31,3. Обозначим a ≈ 22,4; b ≈ 24,7; с ≈ 31,3.

Решение при помощи натуральных таблиц. Имеем:

откуда А ≈ 45°20&#146 (с округлением до 10&#146).

откуда В ≈ 51°30&#146 и, наконец, С ≈ 180° — (45°20&#146 + 51°30&#146) ≈ 83°10&#146.

Решение при помощи логарифмических таблиц. Имеем:

sin А = 2S /_bc, lg sin А = lg 2S — lg b — lg c.

Видео:9 класс. Геометрия. Решение треугольниковСкачать

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это: