Исчезновение клетки в треугольнике объяснение (4 видео)

Исчезающая клетка и числа Фибоначчи ⁠

Содержание

совместно с Григорием Мерзоном
В мире математических парадоксов
Парадокс кучи и парадокс «Лысого»
Парадокс лжеца
Парадокс Тесея
Парадокс Абилина
Парадокс Симпсона и феномен Уилла Роджерса
Исчезновение клетки
Откуда взялась пустая клетка?
📸 Видео

Видео:The disappearance of the cell - the task of mindfulness - Исчезновение клеткиСкачать

совместно с Григорием Мерзоном

Квадрат $8times 8$ можно разрезать на четыре части из которых складывается… прямоугольник $5times 13$ площадью $65!$

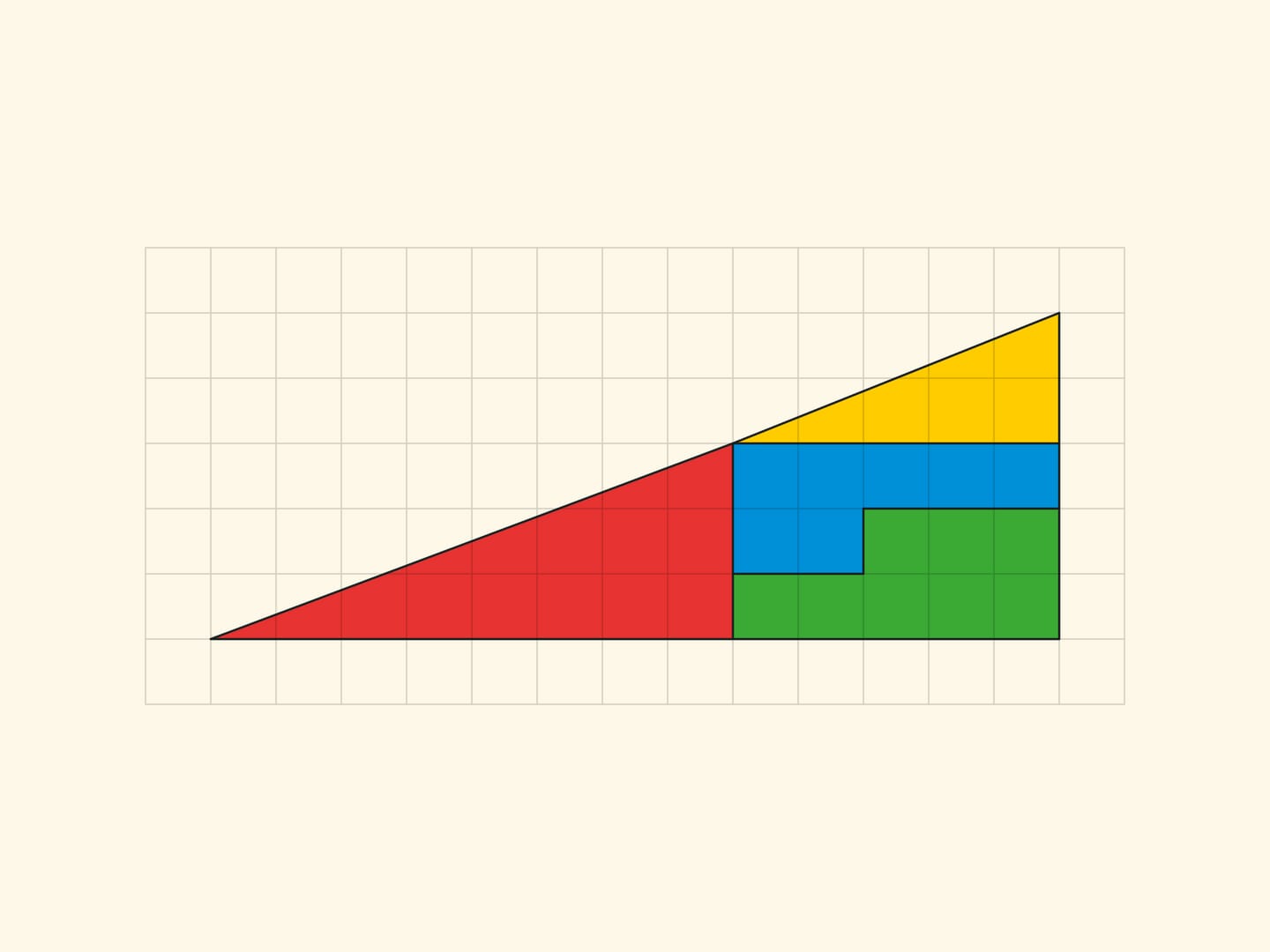
Ещё один известный геометрический софизм: прямоугольный треугольник с катетами $5$ и $13$ разрезается на четыре части, из которых складывается тот же прямоугольный треугольник, но уже с одной пустой клеткой!

Но постойте, площадь фигуры равна сумме площадей частей, из которых она составлена. Поэтому при перекладывании она не может измениться. В чём же нестыковка?

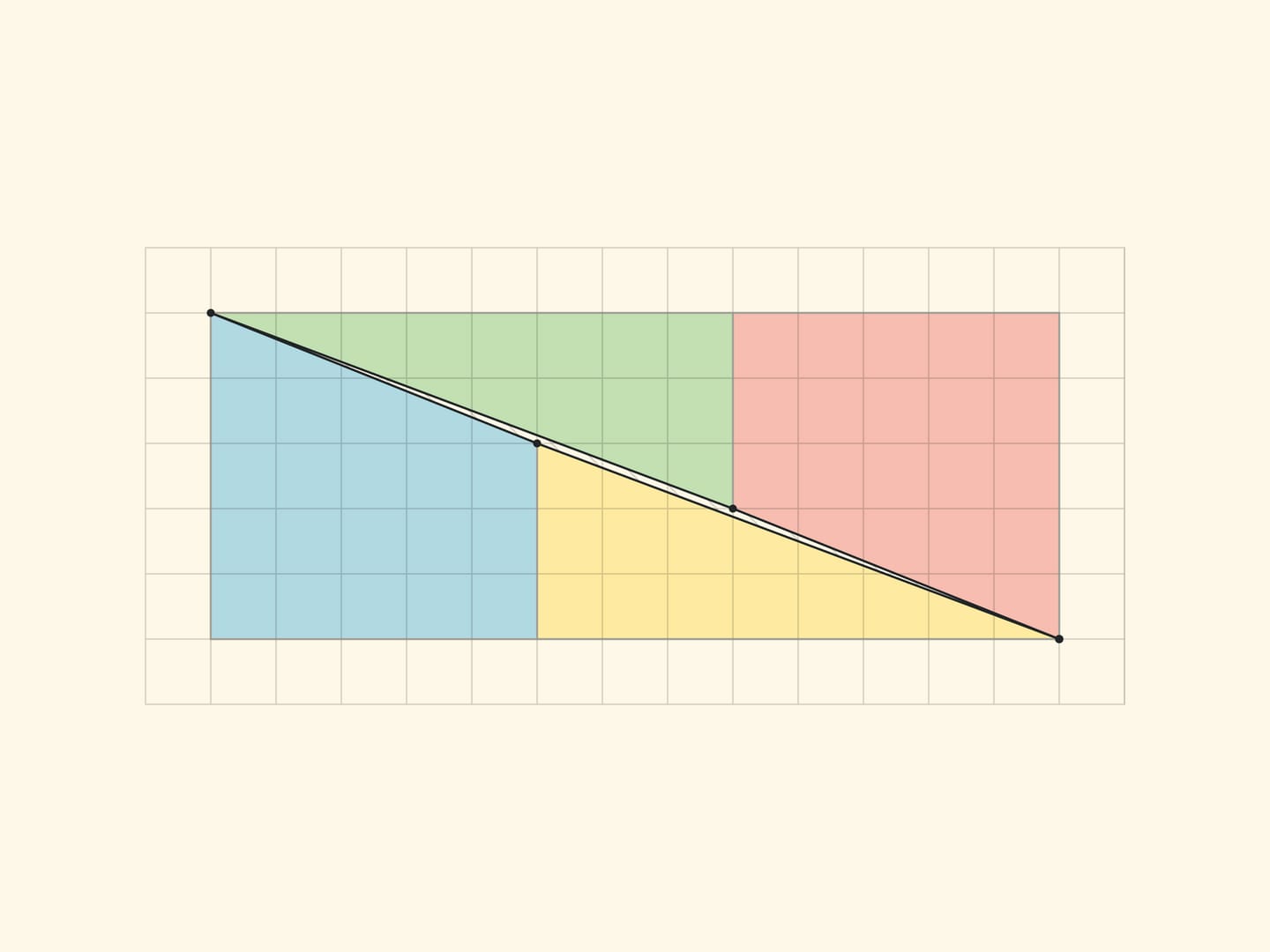
Объяснение парадокса в обоих случаях по сути одинаковое — рассматриваются не те фигуры, которые описывали. В «Парадоксе шахматной доски», представленном шахматистом и автором головоломок Сэмюэлем Лойдом в середине XIX века на шахматном конгрессе, честный квадрат перекладывается не в прямоугольник, а в прямоугольник без вытянутого, почти незаметного глазу параллелограмма единичной площади (вытянутого вдоль диагонали прямоугольника). В парадоксе с треугольниками, придуманном Мартином Гарднером в середине XX века, обе гипотенузы (исходного и получающегося треугольника) на самом деле не являются прямыми: составленная из них фигура также является параллелограммом единичной площади.

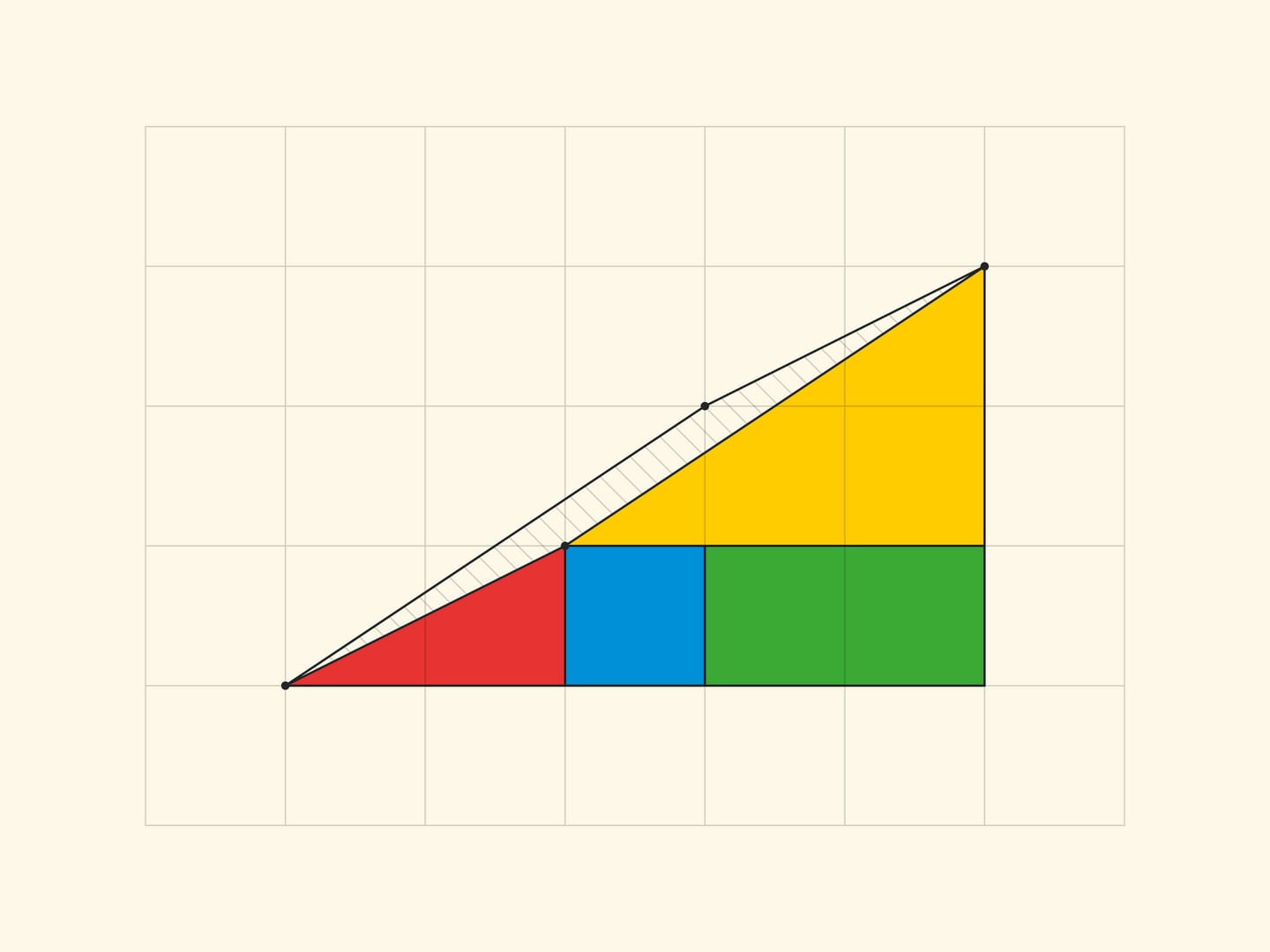
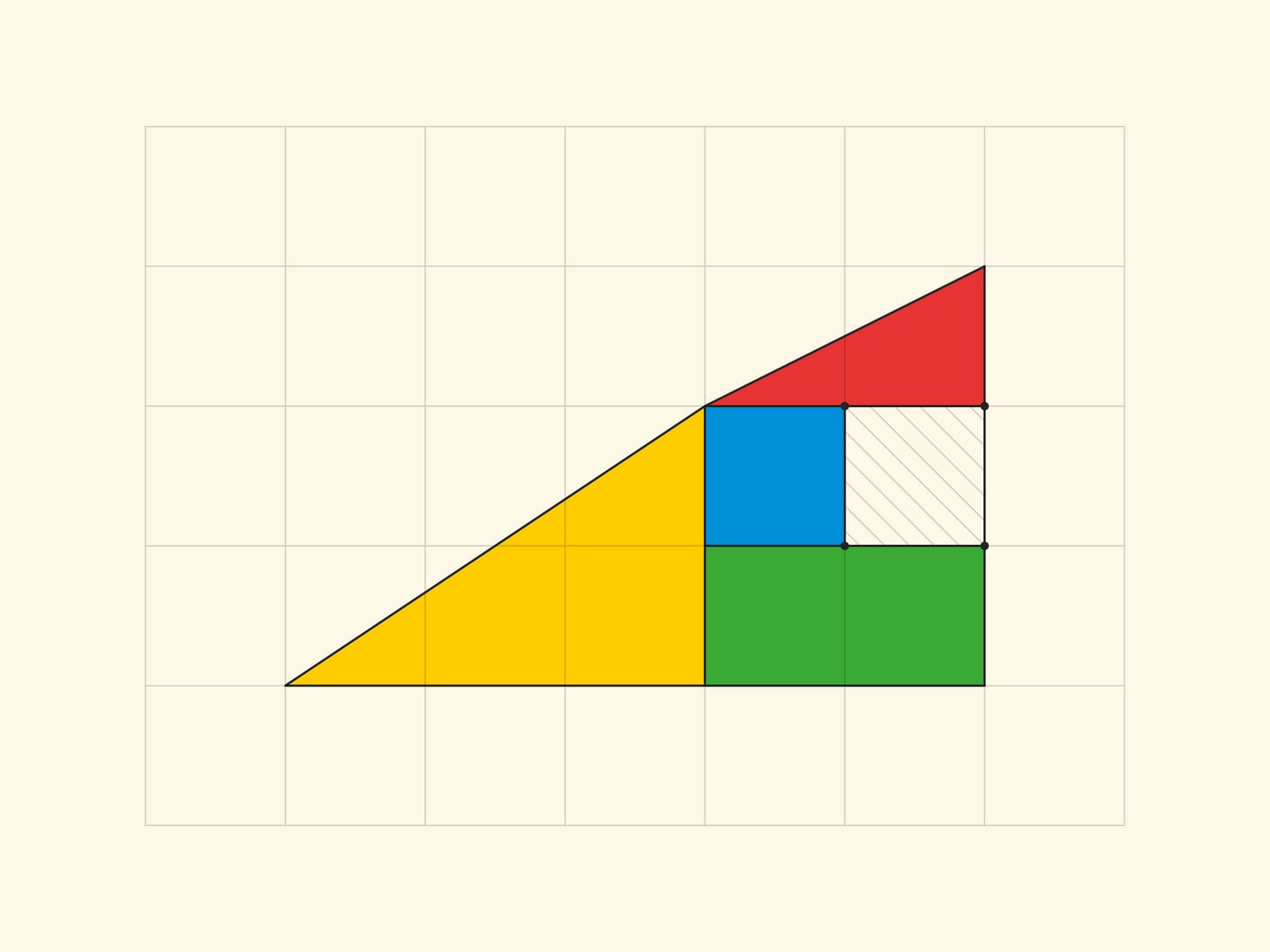
Чтобы было легче разглядеть этот параллелограмм, посмотрим на аналог «треугольника Гарднера» меньшего размера — со сторонами $3$ и $5$.

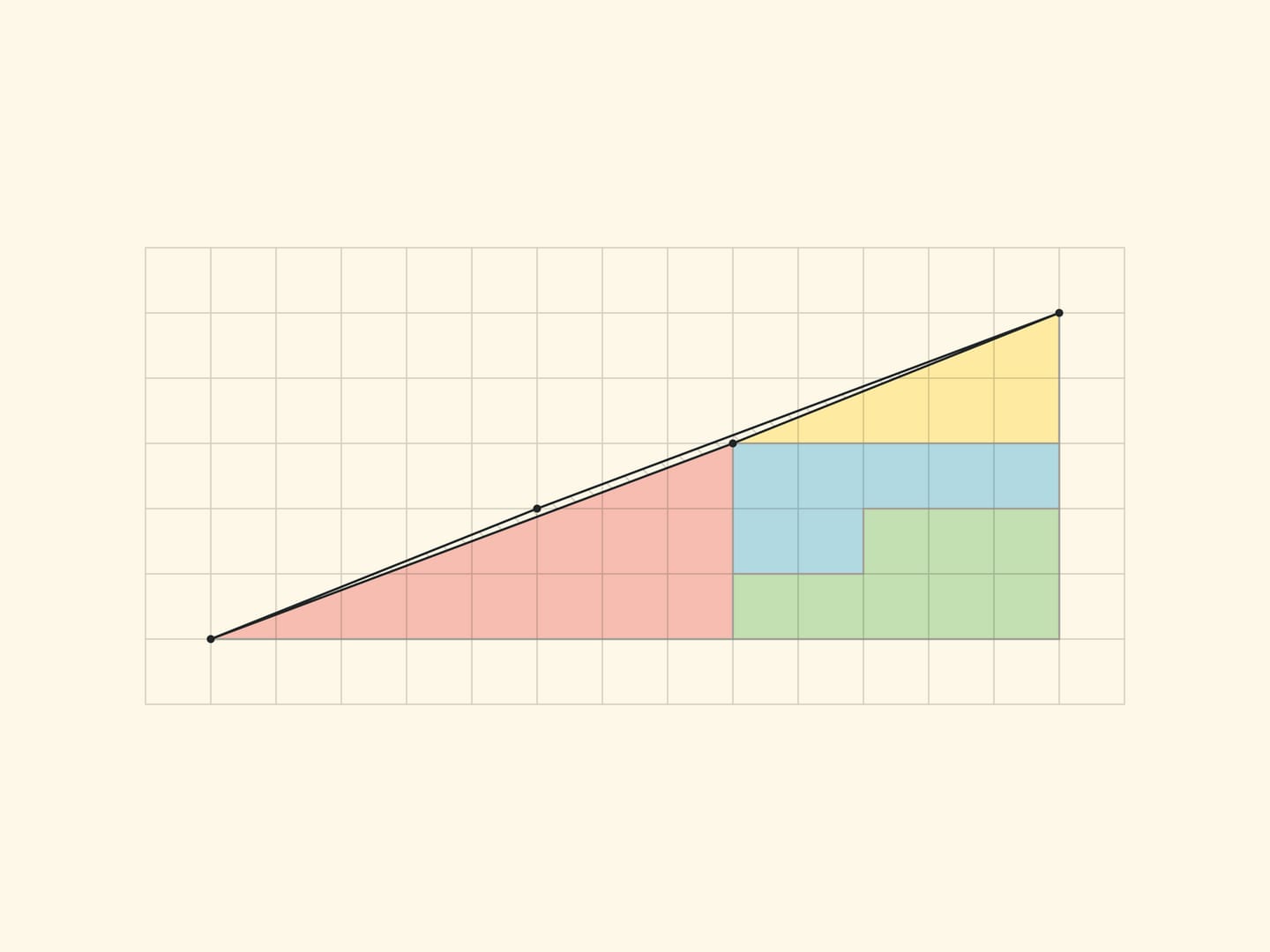
Все вершины всех частей лежат в узлах квадратной сетки. И в том, что границы частей не складываются в прямую линию, а образуют стороны параллелограмма (с вершинами в узлах), легко убедиться, посчитав по клеточкам наклон каждого отрезка. В прямоугольнике $5times 13$ в жёлтом треугольнике отношение катетов равно $tg alpha=dfrac$, а для синей трапеции тангенс «того же» угла равен $dfrac$. Для софизма с треугольником: в варианте Гарднера $dfracne dfrac$, в уменьшенном варианте $dfracne dfrac$. Во всех случаях стороны параллелограмма, как и должно быть, попарно равны и параллельны. Вершины параллелограмма лежат в узлах сетки, а вот внутри параллелограмма нет ни одного узла. Что, впрочем, неудивительно, если вспомнить, что площадь равна единице и ⁠ ⁠ формулу Пика .

Разобравшись с нестыковкой, задумаемся, как конструировать подобные софизмы. Можно заметить, что встречавшиеся числа $1,$ $2,$ $3,$ $5,$ $8,$ $13$ являются началом знаменитой последовательности чисел Фибоначчи

Эта последовательность задаётся рекуррентным соотношением $$ F_n=F_+F_ $$ и парой начальных чисел $F_0=1$, $F_1=1$.

Между числами Фибоначчи существует много интересных соотношений. В $1680$ году французский астроном итальянского происхождения Джованни Доминико Кассини, открывший спутники Сатурна и щель в его кольцах, заметил такое соотношение: $F_cdot F_-F_n^2=(-1)^n$, которое теперь называют его именем.

При $n=6$ получается равенство $5cdot 13-8^2=1$ — знакомые по «Парадоксу шахматной доски» числа и знакомое увеличение на единицу! А вот принять за сторону квадрата число Фибоначчи с нечётным номером нельзя — детали в соответствующий прямоугольник можно сложить только с наложением (в пересечении — всё тот же параллелограмм единичной площади).

В «треугольнике Гарднера» катеты маленьких (настоящих и не меняющих площадь) треугольников являются числами Фибоначчи: у красного — 3 и 8, у жёлтого — 2 и 5. Соответственно стороны прямоугольника (в котором и происходит увеличение на клетку) получаются: до перекладки — 3 и 5, а после перекладки — 2 и 8. Увеличение площади прямоугольника на клетку обеспечивает соотношение на четыре последовательных числа Фибоначчи: $F_cdot F_-F_cdot F_=(-1)^n$, которое можно получить из соотношения Кассини и рекуррентного соотношения. Для $n=6$ получается равенство $8cdot 2-5cdot 3=1$, на котором основан «треугольник Гарднера».

Таким образом, софизмы построены на том, что размеры фигур и частей, из которых они составляются, суть нескольких подряд идущих числах Фибоначчи. Опираясь на эти соотношения можно построить аналогичные софизмы и для фигур больших размеров. В варианте Лойда надо не забывать про чётность, а в варианте Гарднера — если желать, чтобы площадь собиралась в квадратную клетку, придётся увеличивать количество частей, из которых составлен основной прямоугольник.

Для чисел Фибоначчи существует и явное, а не рекуррентное, задание, называемое формулой Бине $$ F_n=frac<sqrt>Big(frac<1+sqrt>Big)^n-frac<sqrt>Big(frac<1-sqrt>Big)^n. $$ Отметим, что хотя числа Фибоначчи целые, в формуле для них возникает число иррациональное — золотое сечение $phi=dfrac2$.

Первая скобка в формуле Бине равна примерно $1618$, а вторая скобка — число отрицательное и по модулю меньшее единицы (примерно $-0618$). Значит, числа Фибоначчи быстро растут, а точнее, $F_nsimdfrac1varphi^n$. Это объясняет, почему с ростом $n$ щель в виде параллелограмма становится всё уже и обман всё сложнее заметить (сравните, например, маленький и большой «треугольники Гарднера»). Действительно, наклоны разных отрезков в софизмах имеют вид $dfrac<F_>$, а с ростом $n$ эти отношения становятся всё ближе к $phi^2$ и практически неразличимы.

Появившийся единичный параллелограмм и его диагональ являются объектами красивой науки, начала которой заложил Герман Минковский, — геометрии чисел. Более точно — геометрической интерпретации цепных дробей.

Видео:Как это решить?Скачать

В мире математических парадоксов

Доброго времени суток, уважаемое хабрасообщество.

Сегодня я хотел бы затронуть такую увлекательную тему, как математические парадоксы. По данной теме на хабре уже было опубликовано несколько замечательных статей (1,2,3,4,5), но в математике интересные парадоксы этой выборкой далеко не исчерпываются.

Поэтому попробуем рассмотреть другие занимательные парадоксы (а некоторые и «не совсем» парадоксы), которые пока еще не получили здесь должного освещения.

Парадокс кучи и парадокс «Лысого»

Данные парадоксы известны еще с древности. Для начала сформулируем и рассмотрим парадокс кучи, связанного с неопределенностью понятия «куча»:

«если к одному зерну добавлять по зёрнышку, то в какой момент образуется куча?»
или обратная формулировка:
«удаляя из кучи в 1 млн зёрен по одному зёрнышку, с какого момента она перестаёт быть кучей?»

Формулировка парадокса основана на очевидной предпосылке, согласно которой одно зёрнышко не образует кучи, и индуктивной предпосылке, по которой добавление одного зернышка к совокупности, кучей не являющейся, несущественно для образования кучи. Из этих предпосылок следует, что никакая совокупность из сколь угодно большого количества зёрен не будет образовывать кучи, что противоречит представлению о существовании кучи из зёрен. Очевидно, что эти рассуждения приводят к неправильным выводам.

Однако до самого недавнего времени не было ясно, какие тогда рассуждения здесь использовать. Лишь с появлением теории нечетких множеств Лофти Заде и нечеткой логики стало ясно, что здесь уместны нечеткие расуждения, поскольку имеется в наличии классический объект нечеткой логики — неопределенное понятие «быть кучей». Данные объекты в нечеткой логике интерпретируются как имеющие неточное значение, характеризуемое некоторым нечётким множеством.

Согласно таким рассуждениям заключение на каждом шаге остается прежним, но принадлежность его правильности уменьшается с каждым шагом. Когда эта принадлежность падает меньше 50%, то более правильным становится противоположное заключение.

Аналогичные рассуждения можно применить и к парадоксу «Лысого»:
«Если волосы с головы выпадают по одному, с какого момента человек становится лысым?»

Парадокс лжеца

Если утверждение на картинке истинно, значит, исходя из его содержания, верно то, что оно — ложно; но если оно — ложно, тогда то, что оно утверждает, неверно; значит, неверно, что утверждение на картинке — ложно, и, значит, это утверждение истинно.

Парадокс лжеца демонстрирует расхождение разговорной речи с формальной логикой, вводя высказывание, которое одновременно и истинно и ложно. В рамках формальной логики данное утверждение не доказуемо и неопровержимо, поэтому решения данного парадокса не существует, но существуют различные варианты его устранения.

Для этого можно применить рассуждения используемые в предыдущем разделе, для этого положим, что утверждение истинно на 0,5, тогда оно и ложно на 0,5, то есть не всякую фразу можно назвать целиком ложной или целиком истинной — «в чем-то высказывание на картинке лжет, а в чем-то — говорит правду»

К такому же выводу можно придти с помощью тройственной логики. В ней есть три степени истинности: «истина», «ложь» и «неопределенно». Под «неопределенно» понимается промежуточное по смыслу значение между истиной и ложью. К данной степени истинности и относят парадокс лжеца.

Как уже говорилось это не решения парадокса лжеца, а всего лишь объяснения, почему данный парадокс возникает в классической двузначной логике высказываний. Они свидетельствует, что строгое деление всех высказываний на истинные и ложные в данном случае неприменимо, поскольку ведет к парадоксу.

В настоящее всемя многие придерживаются такой точки зрения, что данное высказывание вообще не является логическим утверждением, и применять к нему классические методы формальной логики бессмысленно.

Парадокс Тесея

Данный парадокс можно сформулировать следующим образом:

«Если все составные части исходного объекта были заменены, остаётся ли объект тем же объектом?»

Было предложено несколько решений этого парадокса. Согласно философской школе Аристотеля существует несколько описывающих объект причин: форма, материал и суть вещи (которая, по учению Аристотеля, является самой важной характеристикой). Исходя из этого корабль остался тем же, так как его суть не поменялась, лишь изменился износившийся материал.

В следующем решении предложили дать аргументу «тот же» количественную и качественную характеристику. В таком случае, после смены досок корабль Тесея окажется количественно тем же, а качественно — уже другим кораблём.

В последнее время для решения парадокса Тесея предложили использовать 4-х мерную интерпретацию, в которой 3-х мерный корабль имеет также протяженность в 4 измерении-времени. Получившийся 4-х мерный корабль на протяжении временного ряда количественно идентичен с собой. Но отдельные «временные срезы» качественно могут отличаться друг от друга.

Парадокс Абилина

Данный парадокс заключается в том, что группа людей может принять решение, противоречащее возможному выбору любого из членов группы из-за того, что каждый индивидуум считает, что его цели противоречат целям группы, а потому не возражает.

Парадокс был описан Джерри Харви в статье The Abilene Paradox and other Meditations on Management. Имя парадоксу дано по мотивам следующего анекдота, описанного в этой статье:

В один жаркий техасский вечер некая семья играла в домино на крыльце до тех пор, пока тесть не предложил съездить в Абилин отобедать. Жена сказала: «Звучит неплохо». Муж, несмотря на то, что поездка обещала быть долгой и жаркой, подумал, что надо бы подстроиться под других, и произнёс: «По-моему, неплохо; надеюсь, что и твоя мама не откажется». Тёща же ответила: «Конечно, поехали! Я не была в Абилине уже давно».
Дорога была жаркой, пыльной и долгой. Когда же они наконец приехали в кафетерий, еда оказалась невкусной. Спустя четыре часа они, измученные, вернулись домой.

Один из них произнёс неискренне: «Верно, неплохая была поездка?». Тёща на это сказала, что, на самом деле, она бы лучше осталась бы дома, но поехала, раз уж остальные трое были полны энтузиазма. Муж сказал: «Я был бы рад никуда не ездить, поехал лишь чтобы доставить остальным удовольствие». Жена произнесла: «А я поехала, рассчитывая на радость остальных. Надо было быть сумасшедшим, чтобы добровольно отправиться в эту поездку». Тесть ответил, что он предложил это лишь потому, что ему показалось, что остальным скучно.

И они сидели, ошеломлённые тем, что поехали в поездку, которой никто из них не хотел. Каждый из них предпочёл бы спокойно наслаждаться тем днём.

Данный парадокс легко объясняется различными социологическими науками, подтверждающими, что человек редко совершает поступки, противоречащие поступкам его группы. Думаю многие не раз сталкивались с данном парадоксом и в своей жизни.

Парадокс Симпсона и феномен Уилла Роджерса

Замечу, что данные парадоксы являются «кажущимися», то есть они могут возникнуть на интуитивном уровне, но если провести вычисления, то легко убедиться, что никакого парадокса не возникает.

Для иллюстрации парадокса Симпсона рассмотрим пример, описанный известным популяризатором математики Мартином Гарднером.

Пусть мы имеем четыре набора камней. Вероятность вытащить чёрный камень набора № 1 выше, чем из набора № 2. В свою очередь, вероятность вытащить чёрный камень из набора № 3 больше, чем из набора № 4. Объединим набор № 1 с набором № 3 (получим набор I), а набор № 2 — с набором № 4 (набор II). Интуитивно можно ожидать, что вероятность вытащить чёрный камень из набора I будет выше, чем из набора II. Однако, в общем случае такое утверждение неверно.

Пример, в котором выполняется парадокс Симпсона:

Черные шары	Белые шары	Вероятность вытащить черный камень
Набор №1	6	7	6/13 ≈ 0,4615
Набор №2	4	5	4/9 ≈ 0,4444
Набор №3	6	3	6/9 ≈ 0,6667
Набор №4	9	5	9/14 ≈ 0,6429

Теперь смешаем наборы №1 и №3 — из которых черные камни можно вытащить с большей вероятностью и наборы №2 и №4 — из которых черные камни можно вытащить с меньшей вероятностью.

Черные шары	Белые шары	Вероятность вытащить черный камень
Набор I	12	10	12/22 ≈ 0,5454
Набор II	13	10	13/23 ≈ 0,5652

Как мы видим из таблицы после смешивания вероятность вытащить черный камень из набора II стала выше чем из набора I.

Математически никакого парадокса тут нет, так как общая вероятность набора зависит от соотношения количества камней черного цвета и обоих цветов, в данном случае в 4 наборе было 9 черных камней, а в первом аж 7 белых, которые больше всего и повлияли на итоговый расклад.

Близок к парадоксу Симпсона и феномен Уилла Роджерса. По сути в них описывается одно и то же явление, но в других терминах.
Думаю многие не раз сталкивались с фразами подобные такой:
«Когда оки покинули Оклахому и переехали в Калифорнию, то повысили средний интеллект обоих штатов»

Эту фразу приписывают Уиллу Роджерсу, в честь чего феномен и получил свое название.

С точки зрения математики никакого парадокса тут тоже нет. Чтобы в этом убедиться достаточно рассмотреть два множества: первое — , а второе — , если число 90 из второго множества перенести в первое, то среднее арифметическое элементов как первого множества так и второго повысится.

Исчезновение клетки

Широкий класс задач на перестановку фигур, обладающих признаками софизмов: изначально в их условие введена замаскированная ошибка. В какой-то мере данные задачи ближе к оптическим иллюзиям, чем к математике.

Для примера расмотрим одну подобную задачу: дан прямоугольный треугольник 13×5 клеток, составленный из 4 частей. После перестановки частей при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка.

Математически парадоксов и таинственного исчезновения площади тут нет. Визуально наблюдаемые треугольники, на самом деле таковымы не являются, гипотенузы в обоих псевдотреугольниках на самом деле являются ломаными линиями (в первом треугольнике она с изломом внутрь, а во втором — наружу). Если наложить треугольник друг на друга, то между их «гипотенузами» образуется параллелограмм, в котором и содержится «пропавшая» площадь.

Видео:Выживший летчик рассказал, что он увидел в Бермудском треугольникеСкачать

Откуда взялась пустая клетка?

“С любой точки зрения нельзя быть слепым”.
Станислав Ежи Лец.

Давно ваш интеллект баловала интересная игра, головоломка, загадка?

Давайте немного отдохнём от систем отопления. Решим одну головоломку, научимся не делать поспешных выводов, не сторониться странного. Как и выбор в пользу одной из систем отопления возможен только после изучения различных аспектов, взвешивания всех «за» и «против», так и здесь – первый взгляд не даёт моментального ответа. Не всё то, что мы видим – таково на самом деле.

Да, необъяснимое, непонятое, новое – порой отталкивает. Однако, просто уходить от малоизвестного, закрывать глаза на необычное – глупо. Если воздушное отопление на базе газовых конвекторов для вас в диковинку, это лишний повод приглядеться получше, послушать побольше. И узнать разные точки зрения.

Но – вернёмся к загадкам, десерту для ума. Иногда так трудно поверить своим глазам. Взгляните на картинку:

Если Вы видите эту головоломку впервые, то кажется, что геометрия сошла с ума. Верно? Оставляем Вас на несколько минут – побалуйте себя вкусными размышлениями, сверьте найденный ответ.

Из-за разных цветов составных частей фигуры кажутся прямоугольными треугольниками. Но если внимательно присмотреться, перед Вами вовсе не треугольники. А – четырёхугольники. Четвёртая вершина находится в месте со прикосновения вершин аквамаринового и красного треугольников.

Присмотритесь к 5-ой вертикальной линии разметки от левого угла фигуры. Аквамариновый треугольник имеет высоту в 2-е клетки, а красный треугольник в этом же месте – немного меньшую (примерно на 0,2 высоты клетки). Таким образом, острые углы аквамаринового и красного треугольников различны.

Верхний четырёхугольник имеет слегка вогнутую вершину в точке соприкосновения аквамаринового и красного треугольников, а нижний – выпуклую вершину. Именно поэтому и выскакивает «лишняя» свободная клетка.