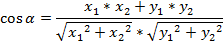Вокруг треугольника можно описать окружность если в параллелограмме (6 видео)

Вокруг треугольника можно описать окружность если в параллелограмме

Какие из данных утверждений верны? Запишите их номера.

1) Вокруг любого треугольника можно описать окружность.

2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.

3) Площадь трапеции равна произведению средней линии на высоту.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Вокруг любого треугольника можно описать окружность» — верно, по свойству треугольника.

2) «Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат» — верно; из всех параллелограммов только в квадрате диагонали равны и перпендикулярны одновременно.

3) «Площадь трапеции равна произведению средней линии на высоту» — верно, по свойству трапеции.

Содержание

Вокруг любого треугольника можно описать окружность.
Какие из данных утверждений верны?
Укажите номер верного утверждения?
Какое из следующих утверждений верно?
Какое из следующих утверждений верно?
Докажите , что диагонали параллелограмма точкой пересечения делятся пополам?
Верно ли что диагонали параллелограмма точкой пересечения делятся пополам?
Выберите верные утверждения : А)в любом прямоугольнике всегда есть большая и меньшая диагонали Б)диагонали квадрата всегда равны В)диагонали квадрата не пересекаются Г)диагонали прямоугольника пересек?
Какое из следующих утверждений верно?
Какие из следующих утверждений верны?
Какие из данных утверждений верны?
. Какое из данных утверждений верно?
🎬 Видео

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вокруг любого треугольника можно описать окружность.

Если в четырехугольнике суммы противоположных сторон равны, то в данный четырехугольник можно вписать окружность.

Если в четырехугольнике сумма противоположных углов равна 180 градусов, то вокруг данного четырехугольника можно описать окружность.

Вектор – это направленный отрезок.

Длина вектора – длина отрезка, задающего вектор.

Нулевой вектор – это точка.

Коллинеарные векторы – векторы которые лежат либо на одной прямой, либо на параллельных прямых.

Сонаправленные векторы – коллинеарные векторы, которые имеют одинаковое направление.

Противоположно направленные векторы – коллинеарные векторы, которые имеют противоположное направление.

Равные векторы – векторы, которые имеют равные длины и направление.

Для сложения или вычитания векторов используют правило треугольника, параллелограмма, многоугольника (стр 198-203).

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон трапеции.

Свойства средней линии трапеции:

· Средняя линия трапеции параллельна основаниям.

· Средняя линия трапеции равна полу сумме оснований.

Теорема о разложении вектора: на плоскости любой вектор можно разложить на сумму двух неколлинеарных векторов, причем коэффициенты разложения определяются единственным способом.

Чтобы найти координаты вектора, надо из координат конца вычесть координаты начала вектора.

Радиус вектор – вектор, имеющий начало в точке пересечения координатных плоскостей.

Координаты радиус вектора равны координатам его конца.

Координаты середины отрезка равны полу сумме координат конца и начала.

Длинна вектора находится как корень квадратный из суммы квадратов его координат.

Расстояние между двумя точками находится как сумма квадратных корней из квадратов разности их координат.

Уравнение прямой: aX+bY+c=0

Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов и их отношение равно радиусу описанной окружности в квадрате.

Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус их удвоенное произведение на косинус угла между ними.

Скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними.

Скалярное произведение ненулевых векторов равно нулю если они перпендикулярны.

Скалярное произведение векторов равно сумме произведений их координат.

Косинус угла между векторами а(X₁;Y₁) и b(X₂;Y₂) находится по формуле:

Угол правильного n-угольника равен:

Около любого правильного многоугольника можно описать окружность и при том только одну.

В любой правильный многоугольник можно вписать окружность и при том только одну.

Центры вписанной и описанной окружностей в правильный многоугольник совпадают.

Окружность вписаннаяв правильный многоугольник касается середин его сторон.

Формула для нахождения стороны правильного n-угольника через радиус описпнной вокруг него окружности:

Формула для нахождения радиуса вписанной в n-угольник окружности через радиус описанной окружности:

Видео:№709. Докажите, что если около параллелограмма можно описать окружность, то этот параллелограммСкачать

Какие из данных утверждений верны?

Математика | 5 — 9 классы

Какие из данных утверждений верны?

1) Вокруг любого треугольника можно описать окружность.

2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.

3) Площадь трапеции равна произведению средней линии на высоту.

4) В тупоугольном треугольнике все углы тупые.

5) В любом параллелограмме диагонали точкой пересечения делятся пополам.

6) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.

Ответ : 1), 2), 3), 5), 6).

Видео:Вокруг любого параллелограмма можно описать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Укажите номер верного утверждения?

Укажите номер верного утверждения.

1)Около любого треугольника можно описать окружность.

2)Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его сторонам.

3)В любом вписанном четырёхугольнике сумма противоположных углов равна 180 гр.

4)Около любого параллелограмма можно описать окружность.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Какое из следующих утверждений верно?

1)Точка пересечения двух окружностей равноудалена от центров этих окружностей.

2)В параллелограмме есть два равных угла.

3)Площадь прямоугольного треугольника равна произведению длин его катетов.

Видео:Вокруг любого треугольника можно описать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Какое из следующих утверждений верно?

1)смежные углы равны, 2)через любую точку лежащую вне окружности, можно провести две касательные к этой окружности, 3)площадь параллелограмма равна половине произведения его диагоналей.

Видео:№708. Докажите, что можно описать окружность: а) около любого прямоугольника; б) около любойСкачать

Докажите , что диагонали параллелограмма точкой пересечения делятся пополам?

Докажите , что диагонали параллелограмма точкой пересечения делятся пополам.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Верно ли что диагонали параллелограмма точкой пересечения делятся пополам?

Верно ли что диагонали параллелограмма точкой пересечения делятся пополам.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Выберите верные утверждения : А)в любом прямоугольнике всегда есть большая и меньшая диагонали Б)диагонали квадрата всегда равны В)диагонали квадрата не пересекаются Г)диагонали прямоугольника пересек?

Выберите верные утверждения : А)в любом прямоугольнике всегда есть большая и меньшая диагонали Б)диагонали квадрата всегда равны В)диагонали квадрата не пересекаются Г)диагонали прямоугольника пересекаются и точкой пересечения делятся пополам.

Видео:Когда в параллелограмм можно вписать окружность. 15 задание ОГЭСкачать

Какое из следующих утверждений верно?

1) Диагонали ромба точкой пересечения делится пополам 2) В тупоугольном треугольнике все углы тупые 3) Каждая из биссектрис равнобедренного треугольника являются его высотой.

Видео:Любой параллелограмм можно вписать в окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Какие из следующих утверждений верны?

1. На плоскости существует единственная точка, равноудалённая от концов отрезка.

2. В любой треугольник можно вписать окружность.

3. Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Какие из данных утверждений верны?

1)вокруг любого треугольника можно описать окружность2)если в параллелограмме диагонали равны и перпендикулярны то этот параллелограмм — квадрат3)площадь трапеции равна произведению средней линии на высоту.

Видео:№696. Докажите, что если в параллелограмм можно вписать окружность, то этот параллелограмм — ромб.Скачать

. Какое из данных утверждений верно?

В ответе запишите номер верного утверждения.

1) В любом параллелограмме диагонали точкой пересечения делятся пополам.

2) Средняя линия трапеции равна половине большего основания.

3) Синус острого угла прямоугольного треугольника равен отношению гипотенузы к противолежащему катету.

4) Если в треугольнике есть острый угол, то этот треугольник остроугольный.

Если вам необходимо получить ответ на вопрос Какие из данных утверждений верны?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Математика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

1)5 + 4 = 9(кг) — всего купила 2)1890 : 9 = 210(тг) — за 1 кг 3)210 * 4 = 840(тг) — за 4 кг 4)210 * 5 = 1050(тг) — за 5 кг.

Х будет рано 8, 1. Простое же уравнение.

А + b = 7620, a — b = 5028 ; a = 4295, a — b = 4295 ; b = 52100, a + b = 104248 ; a = 8500, a — b = 7500. Удачи)).

1 k = 9140 2 c = 3375 это легко.

Всего в магазин привезли 63 кг конфет. За день пришло 3 покупателя. Каждый покупатель купил по 9 кг конфет. Вопрос : Сколько осталось конфет в магазине? Пойдёт.

У Жени было 63 рубля , он купил 9 тетрадей по 3 р. Сколько осталось денег у Жени.

S = x * (1 + %) ^ n S = 150000(1 + 0. 14) ^ 3 = 150000 * 1. 14 ^ 3 = 222231. 6 Ответ : 222231. 6.

9) 10) Человек, стоящий на пляже, видит горизонт на 5, 6 км. Значит, Человек на пляже возвышается над горизонтом на 2, 45 м. Или он такого роста (что вряд ли), или он стоит на кучке песка. Если он хочет видеть горизонт на 7, 2 км, то должен под..

1)178 а остаток1, 178 умножаем на 2 = 356 + 1 = 3572)184 а остаток 2, 184умножаем на 3 = 552 + 2 = 5543)161 а остаток 3, 161 умножаем на 4 = 644 + 3 = 6474)122 а остаток 2, 122 умножаем на 6 = 732 + 2 = 735.

Один человек, так как для всего нетрудно много дел.