Системы синтеза реалистических изображений должны обеспечивать передачу всех свойств моделируемого объекта: объемность, расположение, передачу полутонов, тени, освещение, текстуры поверхности. Чем выше степень реалистичности изображения, тем больше требуется вычислений для его формирования.
Генерация объемных изображений представляет сложную вычислительную задачу, в связи этим на практике выполняют ее декомпозицию. Сложные изображения формируют из фрагментов объектов, для чего их разбивают на составные части. Процесс разбиения поверхности объектов на полигоны получил название тесселяции.
В настоящее время появилось большое разнообразие графических акселераторов, которые имеют различные аппаратные графические функции для закраски трехмерных объектов, удаления невидимых частей, наложения текстур и т.п. Для использования преимуществ 3D-ускорителей необходимо сначала программно произвести тесселяцию исходных объектов, а затем передать полученные полигональные области для дальнейшей обработки акселератору.
На практике наиболее часто производится разбиение изображений на треугольники.
Это объясняется следующими причинами:
• треугольник является простейшим полигоном, вершины которого однозначно задают грань;
• любую область можно гарантировано разбить на треугольники;
• вычислительная сложность алгоритмов разбиения на треугольники существенно меньше, чем при использовании других полигонов;
• реализация процедур рендеринга наиболее проста для области, ограниченной треугольником;
• для треугольника легко определить три его ближайших соседа, имеющих с ним общие грани.
Процесс разбиения полигональной области со сложной конфигурацией в набор треугольников называется триангуляцией. При анализе или синтезе сложных поверхностей их аппроксимируют сеткой треугольников, и впоследствии оперируют с простейшими полигональными областями, т.е. с каждым из треугольников.
Алгоритм триангуляции:
1. Берем три вершины A1, A2, A3
2. Проверяем образуют ли вектора A1A3, A1A2 и их векторное произведение левую тройку векторов.
3. Проверяем нет ли внутри треугольника A1A2A3 какой-либо из оставшихся вершин многоугольника.
4. Если оба условия выполняются, то строим треугольник A1A2A3, а вершину A2 исключаем из многоугольника, не трогая вершину A1, сдвигаем вершины A2 (A2 на A3), A3 (A3 на A4)
5. Если хоть одно условие не выполняется, переходим к следующим трем вершинам.
6. Повторяем с 1 шага, пока не останется три вершины.
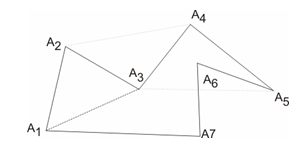
Рис.1 Алгоритм триангуляции невыпуклого многоугольника
На рисунке 1
• треугольник A1A2A3 удовлетворяет обоим условиям (п.2, п.3);
• треугольник A2A3A4 не удовлетворяет условию (п.2);
• треугольник A3A4A5 не удовлетворяет условию (п.3).
Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Триангуляция многоугольников
Задача: разбить произвольный многоугольник на треугольники.
- Клас, что-то наподобие списка, где можно двигаться вперед-назад и конец соединен с началом. То есть замкнутый круг, элементами которого будут объекты описаны пунктом ниже.
- Клас для представления точки. В нем, как полагается, должны быть координаты х и у. Так же еще одно поле в котором записано значение угла соответствующего этой точке в многоугольнике
- Функция, на вход которой идут два векторы, а на выход — угол между ними
- Функция, на вход которой идет точка и треугольник, на выход — признак, лежит ли точка внутри треугольника.
Теперь сам алгоритм.
Подготовка рабочих объективов.
Результатом работы должен быть список треугольников (result), потому создаем пустой список. Рабочий двунаправленный замкнутый список (points), представляющий многоугольник.
Перед стартом просчитываем углы для всех точек многоугольника.
Выбираем любую точку многоугольника как «рабочую» (p(i)).
- Создаем пустой список для хранения временных треугольников.
Если точка слева от «рабочий» (p(i)->left) имеет угол меньше чем 180 градусов и треугольник (p(i), p(i)->left, p(i)->left->left) не содержит внутри себя других точек многоугольника — заносим этот треугольник в наш временный список.
Если точка справа от «рабочий» (p(i)->right) имеет угол меньше чем 180 градусов и треугольник (p(i), p(i)->right, p(i)->right->right) не содержит внутри себя других точек многоугольника — заносим этот треугольник в наш временный список.
Если «рабочая» точка (p(i)) имеет угол меньше чем 180 градусов и треугольник ( p(i)->left, p(i),p(i)->right) не содержит внутри себя других точек многоугольника — заносим этот треугольник в наш временный список. - Если временный список не содержит треугольников — выбираем вместо «рабочий», точку слева от нее и возвращаемся к первому пункту.
Если содержит — выбираем треугольник с минимальной разницей между минимальным и максимальным углом (нужно пересчитать значение углов), заносим его в список result, удаляем из points среднюю точку из треугольника который выбрали а соседним точкам от нее (в points) пересчитываем значения углов, первую точку выбираем в качестве «рабочей» (p(i)).Если в points осталось только две точки — прекращаем работу, список треугольников содержится в res, иначе возвращаемся к первому пункту.
Теперь пара слов об оптимизации алгоритма.
На втором этапе выбирается треугольник с минимальной разницей между минимальным и максимальным углом для того, чтобы треугольник был максимально подобный к правильному, иногда это важно. Если же вам нет разницы как выглядит треугольник — тогда можно не создавать временный список треугольников, а выбрать первый из трех возможных треугольников который не содержит внутри себя другую точку многоугольника и угол, который образует средняя точка треугольника в многоугольнике меньше 180 градусов. Такое упрощение значительно снизит вычислительные затраты.
Еще, если уверены, что многоугольник выпуклый — тогда не нужно проверь содержит ли треугольник другие точки многоугольника.
П.С. Я не встречал такой алгоритм на просторах инета, хотя и уверен, что что-то подобное уже есть.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Конспект урока по математике на тему»Разбиение многоугольника на треугольники»4класс
Разбиение многоугольника
на треугольники
Цели: учить выполнять чертеж; формировать умение делить отрезками многоугольник на данное количество треугольников; закреплять умение определять количество сторон и количество диагоналей в многоугольнике.
1. Математический диктант.
а) Как называется результат сложения двух чисел?
б) Как называются числа, которые складывают?
в) Чему равна сумма 3456 + 0?
г) Запишите равенство 245 – 181 = 63. С помощью сложения проверьте, правильно ли выполнено вычитание.
д) Найдите значение выражения 981 – х, если х = 0.
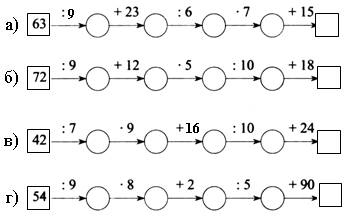
2. Какое число нужно вписать в последнюю клетку цепочки?
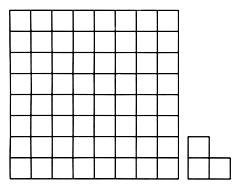
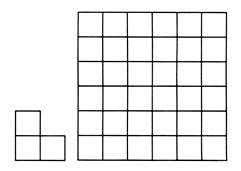
3. Как-то раз Пятачок зашёл в гости к Винни-Пуху. Тот в глубокой задумчивости смотрел на лист бумаги, где были нарисованы квадрат и уголок.
Винни-Пух объяснил, что хочет разрезать квадрат на уголки.
Пятачок внимательно посмотрел на эти фигуры и сказал, что такой квадрат разрезать на такие уголки нельзя. Почему? А вот такой квадрат можно разрезать на уголки. Покажите, как это сделать.
II. Работа по учебнику.
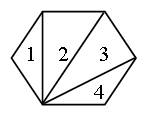
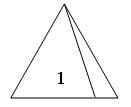
Задание 376. Начертите шестиугольник и проведите все возможные диагонали из одной его вершины.
– На какие фигуры эти диагонали разбивают шестиугольник? (На треугольники.) Сколько треугольников получилось? (4 треугольника.)
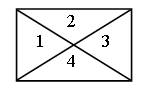
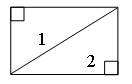
Задание 377. Начертите прямоугольник и разбейте его на 4 треугольника.
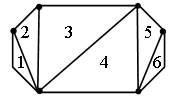
Задание 378. Как называется данный многоугольник? (Восьмиугольник.) Разбейте этот восьмиугольник на 6 треугольников.
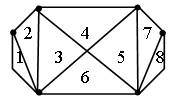
– Разбейте этот же восьмиугольник на 8 треугольников.
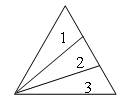
Задание 379. Начертите остроугольный треугольник и разбейте его на 3 треугольника.
Задание 380. Начертите остроугольный треугольник и разбейте его на 2 треугольника так, чтобы один из них был остроугольным, а другой – тупоугольным.
1-й треугольник – остроугольный;
2-й треугольник – тупоугольный.
Задание 381. Разбейте прямоугольник на два прямоугольных треугольника. Используя модель прямоугольника, сделанную из бумаги, убедитесь, что полученные прямоугольные треугольники равны.
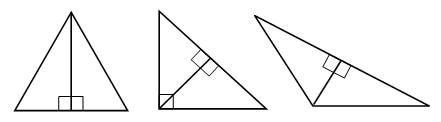
Задание 382. Начертите остроугольный, прямоугольный и тупоугольный треугольники. Разбейте каждый из них на два прямоугольных треугольника.
– Как называется отрезок, с помощью которого такое разбиение можно выполнить? (Высота треугольника.)
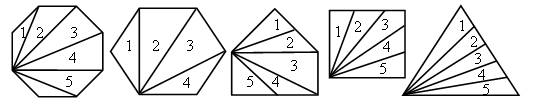
Задание 383. Как называются данные многоугольники? (Семиугольник, шестиугольник, пятиугольник, четырехугольник, треугольник.)
– Каждый многоугольник разбейте на 5 треугольников.
– Как можно разбить многоугольник на треугольники?
🎬 Видео
Математика 5 Треугольники МногоугольникиСкачать

Многоугольники. Математика 8 класс | TutorOnlineСкачать

Как начертить треугольник | 4 способа | Выпуклый многоугольникСкачать

Построение пятиугольника циркулемСкачать

8 класс, 2 урок, Выпуклый многоугольникСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Что такое периметр. Как найти периметр многоугольника?Скачать

КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Выпуклые и невыпуклые многоугольникиСкачать
Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Чему равна сумма углов выпуклого многоугольникаСкачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

МногоугольникСкачать

Математика 5 класс (Урок№28 - Треугольники.)Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Диагональ многоугольникаСкачать

Многоугольники // Математика 1 классСкачать