Как проводить параллельные прямые в кубе (6 видео)

Узнать ещё

Знание — сила. Познавательная информация

Содержание

Сечение куба плоскостью
10 класс. Геометрия. Параллельные прямые в пространстве.
10 класс. Геометрия. Параллельные прямые в пространстве.
Вопросы
Поделись с друзьями
Комментарии преподавателя
1. Тема и цели урока
2. Определение параллельных прямых в пространстве
3. Теорема 1 и ее доказательство
4. Лемма (о двух параллельных прямых, пересекающих плоскость) и ее доказательство
5. Теорема 2 и ее доказательство
6. Итоги урока
Как проводить параллельные прямые в кубе
💥 Видео

Видео:10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Сечение куба плоскостью

Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.

Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.

Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.

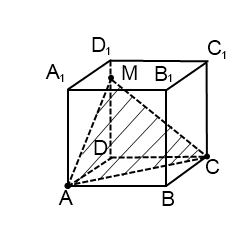
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.

Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.

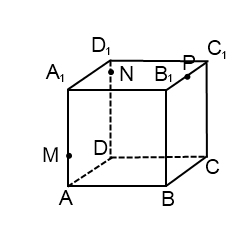
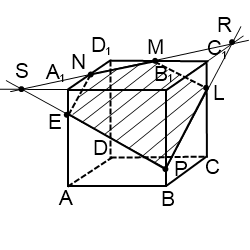
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.

Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.

Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).

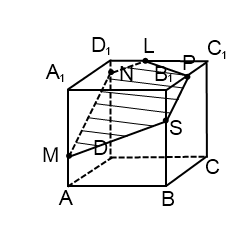
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).

Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.

Пятиугольник MNLPS — искомое сечение.

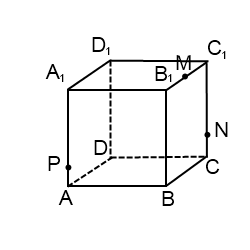
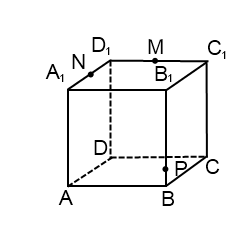
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.

Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).

Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.

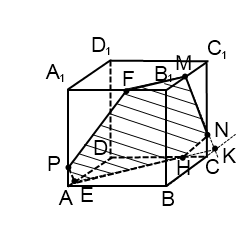
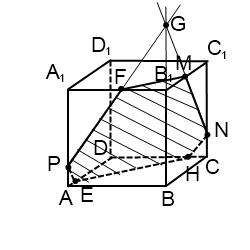
Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).

Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.

Шестиугольник MNHEPF — искомое сечение.

Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.

Работа с прямой PE дает то же сечение MNHEPF.

4) Построить сечение куба плоскостью, проходящей через точку M, N, P.

Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.

Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.

Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.

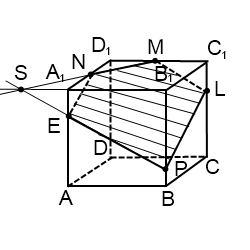
Видео:Параллельные прямые циркулемСкачать

10 класс. Геометрия. Параллельные прямые в пространстве.

Оглавление
Занятия
Обсуждение
О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

1. Тема и цели урока

Мы уже изучали параллельные прямые в планиметрии. Теперь нужно дать определение параллельных прямых в пространстве и доказать соответствующие теоремы.

Видео:4K Как начертить параллельные прямые при помощи циркуля, how to draw parallel linesСкачать

2. Определение параллельных прямых в пространстве

Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются (Рис. 1.).

Обозначение параллельных прямых: a || b.

Видео:Как строить сечение куба? Стереометрия. 10-11 класс | Математика | TutorOnlineСкачать

3. Теорема 1 и ее доказательство

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Дано: прямая а, (Рис. 2.)

Доказать: существует единственная прямая b || a,

Через прямую а и точку , не лежащую на ней, можно провести единственную плоскость α (Рис. 3.). В плоскости α можно провести единственную прямую b, параллельную а, проходящую через точку M (из аксиомы планиметрии о параллельных прямых). Существование такой прямой доказано.

Докажем единственность такой прямой. Предположим, что существует другая прямая с, проходящая через точку M и параллельная прямой а. Пусть параллельные прямые а и с лежат в плоскости β. Тогда плоскость β проходит через точку M и прямую а. Но через точку M и прямую а проходит единственная плоскость (в силу теоремы 2). Значит, плоскости β и α совпадают. Из аксиомы параллельных прямых, следует, что прямые b и с совпадают, так как в плоскости существует единственная прямая, проходящая через данную точку и параллельная заданной прямой. Единственность доказана.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

4. Лемма (о двух параллельных прямых, пересекающих плоскость) и ее доказательство

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Дано: а || b,

Доказать:

Доказательство: (Рис. 4.)

Существует некоторая плоскость β, в которой лежат параллельные прямые а и b. Точка М принадлежит и плоскости α, и прямой а, которая лежит в плоскости β. Значит, М – общая точка плоскостей α и β. А по третьей аксиоме, существует прямая MN, по которой пересекаются эти две плоскости.

Прямая MN пересекается с прямой b.(так как в противном случае, получается, что прямые MN и b параллельные, то есть a = MN, что невозможно, так как прямая а пересекается с плоскостью α в точке М по условию). То есть точка N – это точка пересечения прямой b и плоскости α..

Докажем, что N — это единственная общая точка прямой b и плоскости α. Допустим, что есть другая точка, но тогда прямая bпринадлежит плоскости α (по второй аксиоме). То есть MN = b, что невозможно, так как прямые а и bпараллельны, а прямая а должна пересекаться с прямой MN. Лемма доказана.

Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

5. Теорема 2 и ее доказательство

Если две прямые параллельны третьей, то они параллельны.

Дано:

Доказать: .

Доказательство: (Рис. 5.)

Выберем произвольную точку К на прямой b. Тогда существует единственная плоскость α, проходящая черезточку К и прямую а. Докажем, что прямая bлежит в плоскости α.

Предположим противное. Пусть прямая bне лежит в плоскости α. Тогда прямая bпересекает плоскость α в точке К. Так как прямые bи с параллельны, то, согласно лемме, прямая с также пересекает плоскость α. Прямые а и с также параллельны, значит, по лемме, прямая а также пересекает плоскость α, но это невозможно, так как прямая а лежит в плоскости α. Получили противоречие. То есть, предположение было неверным, а значит, прямая bлежит в плоскости α.

Докажем, что прямые а и b не пересекаются. Предположим противное. Пусть прямые а и bпересекаются в некоторой точке М. Но тогда получается, что через точку М проходят две прямые а и b, параллельные прямой с, что невозможно в силу теоремы 1. Получили противоречие. Значит, прямые а и b не пересекаются.

Мы доказали, что прямые а и b не пересекаются и что существует плоскость α, в которой лежат прямые а и b. Значит, прямые а и bпараллельны (по определению), что и требовалось доказать.

Видео:Параллельность прямых. Практическая часть. 10 класс.Скачать

6. Итоги урока

Итак, мы дали определение параллельных прямых и доказали теорему о параллельных прямых в пространстве. Также мы доказали важную лемму о пересечении параллельными прямыми плоскости и с помощью этой леммы доказали теорему: если две прямые параллельны третьей, то они параллельны. Эта теория будет использоваться дальше и для доказательства других теорем, и для решения задач.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Как проводить параллельные прямые в кубе

И.М. Смирнова , В.А. Смирнов

ЛЕКЦИЯ 7: СЕЧЕНИЯ ПРОСТРАНСТВЕННЫХ ФИГУР

Рассмотрим вопрос об исследовании и построении сечений многогранников плоскостью. Задачи на построение сечений многогранников, определение вида сечений или вычисление элементов этих сечений часто включаются в различные контрольные и проверочные работы, конкурсы и олимпиады по математике. Решение таких задач способствует развитию пространственных представлений, выработке практических навыков изображения пространственных фигур.

Выясним, какими могут быть сечения куба плоскостью.

Если плоскость пересекает три ребра куба, выходящих из одной вершины, то в сечении получается треугольник (рис. 1). При этом если отсекаемые плоскостью отрезки ребер равны, то в сечении получается равносторонний треугольник, если равны два отрезка из трех, то получается равнобедренный треугольник, наконец, если все три отрезка различны, то в сечении получается разносторонний треугольник.

Покажем, что в сечении куба плоскостью не могут получаться прямоугольный или тупоугольный треугольники. Для этого обозначим отрезки, выходящие из вершины куба и отсекаемые плоскостью, соответственно a , b и c . По теореме Пифагора имеем равенства: AB 2 = a 2 + b 2 , AC 2 = a 2 + c 2 , BC 2 = b 2 + c 2 . Из этих равенств следует, что AB 2 AC 2 + BC 2 и, значит, угол C – острый. Аналогично, углы A и B – также острые, т.е. треугольник ABC – остроугольный. Таким образом, в сечении куба плоскостью можно получить только остроугольный треугольник и нельзя получить прямоугольный или тупоугольный треугольники.

Выясним, какие четырехугольники могут получаться в сечении куба плоскостью.

Ясно, что если плоскость параллельна одной из граней куба, то в сечении получается квадрат (рис. 2). Если плоскость параллельна одному из ребер куба, то в сечении получается прямоугольник (рис. 3). Если плоскость пересекает четыре параллельных ребра куба, то в сечении получается параллелограмм (рис. 4).

Самостоятельно выясните, может ли в сечении куба плоскостью получиться: а) трапеция; б) равнобедренная трапеция; в) неравнобедренная трапеция; г) прямоугольная трапеция; д) тупоугольная трапеция?

Поскольку для любых четырех граней куба обязательно найдутся две из них, параллельные между собой, то в четырехугольнике, являющемся сечением куба плоскостью обязательно найдутся две параллельные стороны. Таким образом, в сечении куба плоскостью не может получиться четырехугольник, у которого нет параллельных сторон.

На рисунке 5 показано сечение куба плоскостью в форме пятиугольника ABCDE . Прямые AB и DE , CD и AE параллельны, как линии пересечения двух параллельных плоскостей третьей плоскостью.

Таким образом, в сечении куба плоскостью может получиться только тот пятиугольник, у которого имеется две пары параллельных сторон. В частности, не может получиться правильный пятиугольник.

На рисунке 6 показано сечение куба плоскостью в форме шестиугольника ABCDEF . Прямые AB и DE , BC и EF , CD и AF параллельны, как линии пересечения двух параллельных плоскостей третьей плоскостью.

Таким образом, в сечении куба плоскостью может получиться только тот шестиугольник, у которого имеется три пары параллельных сторон.

Самостоятельно докажите, что в случае, если точки A , B , C являются серединами ребер, то в сечении получается правильный шестиугольник.

Поскольку у куба имеется только шесть граней, то в сечении куба плоскостью не может получиться многоугольник с числом сторон, большим шести.

Рассмотрим теперь вопрос о построении сечений многогранников.

Пусть дано изображение куба и три точки A , B , C , принадлежащие ребрам этого куба, выходящим из одной вершины. Тогда для того чтобы построить сечение куба плоскостью, проходящей через эти точки, достаточно просто соединить их отрезками. Полученный треугольник ABC и будет искомым изображением сечения куба (рис. 1).

Для построения более сложных сечений используют метод «следов», заключающийся в нахождении точки пересечения прямой и плоскости по заданным двум точкам этой прямой и их проекциям на плоскость.

Решим несколько предварительных задач на построение.

Задача 1. Пусть прямая k проходит через точки A , B и известны параллельные проекции A ’ , B ’ этих точек на плоскость p . Требуется найти точку пересечения прямой AB с плоскостью p .

Решение. Через точки A ’ , B ’ проведем прямую k ’ . Тогда пересечение прямой k с прямой k ’ и будет искомым пересечением прямой k с плоскостью p (рис. 7).

Задача 2. Даны точки A , B , C и их параллельные проекции A ’ , B ’ , C ’ на плоскость p . Требуется построить линию пересечения плоскости ABC и плоскости p .

Решение. Используя решение предыдущей задачи, построим точки X и Y пересечения прямых AB и AC с плоскостью p . Прямая XY будет искомой линией пересечения плоскости ABC и плоскости p (рис. 8).

Задача 3. Через данную точку C ( C ’ ) провести прямую, параллельную данной прямой AB ( A ’ B ’ ), и найти ее точку пересечения с плоскостью p .

Решение. Через точку C проводим прямую, параллельную AB . Через точку C ’ проводим прямую, параллельную A ’ B ’ . Точка X пересечения этих прямых и будет искомой (рис. 9).

Используя этот метод, решим задачи на построение сечений куба, пирамиды и призмы.

Задача 4. Построить сечение куба плоскостью проходящей через три точки A , B , C , принадлежащие попарно скрещивающимся ребрам этого куба (рис. 10).

Решение. Найдем пересечение прямой AB , лежащей в плоскости сечения, с плоскостью основания куба. Для этого построим параллельные проекции A ’, B ’ точек A , B на основание куба в направлении бокового ребра куба (рис. 11). Пересечение прямых AB и A ’ B ’ будет искомой точкой P . Она принадлежит плоскости сечения и плоскости основания куба. Следовательно, плоскость сечения пересекает основание куба по прямой CP . Точка пересечения этой прямой с ребром основания куба даст еще одну точку D сечения куба. Соединим точки C и D , B и D отрезками. Через точку A проведем прямую, параллельную BD , и точку ее пересечения с ребром куба обозначим E . Соединим точки E и C отрезком. Через точку A проведем прямую, параллельную CD , и точку ее пересечения с ребром куба обозначим F . Соединим точки A и F , B и F отрезками. Многоугольник AECDBF и будет искомым изображением сечения куба плоскостью (рис. 11 ).

Задача 5. Построить сечение треугольной пирамиды плоскостью, проходящей через три точки A , B , C , принадлежащие ее ребрам (рис. 12).

Решение. Проведем прямую AB и ее точку пересечения с боковым ребром пирамиды обозначим через E . Проведем прямую EC и ее точку пересечения с ребром основания пирамиды обозначим через D . Соединим отрезками точки B и C , A и D . Четырехугольник ABCD будет искомым сечением пирамиды.

Задача 6. Построить сечение шестиугольной пирамиды плоскостью, проходящей через точки A ₁ , C ₁ , E ₁ (рис. 13).

Решение. Проведем прямую A ₁ C ₁ и найдем точку P ее пересечения с прямой AC . Проведем прямую E ₁ C ₁ и найдем точку Q ее пересечения с прямой EC . Проведем прямую PQ , являющуюся линией пересечения плоскостей a и p . Проведем прямую AB и найдем точку V ее пересечения с прямой PQ . Проведем прямую A ₁ V и найдем точку B ₁ ее пересечения с SB . Аналогичным образом строятся и остальные точки D ₁ , F ₁ .

Задача 7. На гранях четырехугольной призмы ABCDA ₁ B ₁ C ₁ D ₁ даны точки K , L и M (рис. 14). Постройте сечение призмы плоскостью, проходящей через эти точки.

Решение. Через точки K , L и M проведем прямые, параллельные боковому ребру призмы, и найдем точки K ’ , L ’ и M ’ их пересечения со сторонами основания. Обозначим N ’ точку пересечения прямых K ’ L ’ и BM ’ . Через точку N ’ проведем прямую, параллельную боковому ребру призмы, и найдем точку N ее пересечения с прямой KL . Через точки N и M проведем прямую, и найдем точку P ее пересечения с ребром BB ₁ . Точка P будет принадлежать искомому сечению. Через точку P и точки K и L проведем прямые, и найдем точки Q и R их пересечения с боковыми ребрами AA ₁ и CC ₁ призмы. Через точки Q и M проведем прямую, и найдем точку S ее пересечения с боковым ребром DD ₁ . Четырехугольник PQSR будет искомым сечением призмы плоскостью.

1. Какой фигурой является сечение куба A . D ₁ плоскостью, проходящей через вершины B ₁ , D и середину ребра CC ₁ ?

2. Какой фигурой является сечение куба A . D ₁ плоскостью, проходящей через середины ребер AB , BC и DD ₁ ?

3. Через середину ребра куба, перпендикулярно скрещивающейся с этим ребром диагонали, проведено сечение. Определите его вид.

Ответ: Правильный шестиугольник.

4. Какой фигурой является сечение куба плоскостью, которая проходит через две противоположные вершины нижнего основания и середину одного из ребер верхнего основания? Найдите его периметр, если длина ребра куба равна 1.

Ответ: Равнобедренная трапеция периметра

5. Через вершины A , C , D ₁ куба A … D ₁ проведено сечение. В каком отношении оно делит диагональ DB ₁ , и какой образует угол с этой диагональю?

6. Может ли в сечении куба плоскостью получиться четырехугольник, изображенный на рисунке 15?

7. Выясните, какие могут быть сечения правильного тетраэдра плоскостью.

Ответ: Правильный, равнобедренный и разносторонний треугольники; квадрат, прямоугольник и четырехугольник с непараллельными сторонами.

8. Каким является сечение тетраэдра ABCD плоскостью, проходящей через середины ребер AB , BC и CD ?

9. Какой фигурой является сечение правильного тетраэдра ABCD плоскостью, проходящей через вершину B и точки M , N — середины соответственно ребер AD , CD ?

10. Может ли в сечении тетраэдра плоскостью получиться четырехугольник, изображенный на рисунке 16?

11. Какие многоугольники можно получить в сечении четырехугольной пирамиды плоскостью?

Ответ: Треугольник, четырехугольник, пятиугольник.

12. Определите вид сечения правильной треугольной призмы плоскостью, проходящей через сторону нижнего основания и середину скрещивающейся с ней стороны верхнего основания.

Ответ: Равнобедренная трапеция.

13. Верно ли утверждение о том, что в сечении правильной шестиугольной призмы плоскостью, проходящей через середины двух соседних боковых ребер и вершину верхнего основания, принадлежащей смежной боковой грани, получается равнобедренная трапеция?

14. Постройте сечение куба плоскостью, проходящей через три точки, расположенные так, как показано на рисунках 17, 18.

15. Постройте сечение куба A . D ₁ плоскостью, проходящей через вершины B ₁ , D и точку H , принадлежащую ребру CC ₁ .

16. Постройте сечение правильной четырехугольной пирамиды плоскостью, проходящей через точки, указанные на рисунке 19 .

17. Как построить сечение правильного тетраэдра ABCD плоскостью, параллельной грани BDC и проходящей через точку K — середину ребра AD ?

18. Постройте сечение правильной шестиугольной призмы плоскостью, проходящей через точки, указанные на рисунке 20.

19. Меньший куб поставлен на больший таким образом, что они имеют общую вершину и их грани попарно параллельны (рис. 21). Постройте сечение полученной фигуры плоскостью, проходящей через три точки, которые принадлежат скрещивающимся ребрам меньшего куба.

Сечения цилиндра плоскостью можно рассматривать как параллельные проекции основания цилиндра на эту плоскость. Поэтому, если плоскость параллельна плоскости основания, то в сечении получается круг, равный основанию. Здесь мы докажем, что если плоскость сечения составляет некоторый угол с плоскостью основания цилиндра и не пересекает основания, то в сечении будет фигура, ограниченная эллипсом.

Напомним, что эллипсом называется геометрическое место точек, сумма расстояний от которых до двух данных точек F ₁ , F ₂ есть величина постоянная, называется эллипсом. Точки F ₁ , F ₂ называются фокусами эллипса.

Таким образом, для точек A эллипса с фокусами F ₁ и F ₂ сумма AF ₁ + AF ₂ постоянна и равна некоторому положительному числу c (рис. 22). Из неравенства треугольника следует, что число c должно быть больше длины отрезка F ₁ F ₂ .

Слово «фокус» в переводе с латинского языка означает «очаг», «огонь», и именно это свойство эллипса послужило основанием для названия точек F ₁ , F ₂ фокусами.

Отрезок прямой F ₁ F ₂ , соединяющий две точки эллипса, называется большой осью.

Отрезок прямой, проходящей через середину большой оси и перпендикулярной этой оси, соединяющий две точки эллипса, называется малой осью эллипса.

Еще И. Кеплер обнаружил, что планеты Солнечной системы движутся вокруг Солнца не по окружностям, как думали раньше, а по эллипсам, причем Солнце находится в фокусах этих эллипсов. Точка орбиты планеты, ближайшая к Солнцу, называется перигелий, а наиболее удаленная — афелий. Однако из-за того, что орбита Земли представляет собой очень мало сжатый эллипс, похожий на окружность, такое приближение и удаление от Солнца незначительно сказывается на температуре. Гораздо большее значение для температуры на поверхности Земли имеет угол падения солнечных лучей. Например, когда Земля бывает в перигелии, в нашем полушарии зима, а когда в афелии — в нашем полушарии лето. Луна, искусственные спутники Земли также движутся вокруг Земли по эллипсам.

Для того чтобы нарисовать эллипс потребуется нить и кнопки. Прикрепим концы нити к фокусам. Карандашом натянем нить так, чтобы его острие касалось бумаги. Будем перемещать карандаш по бумаге так, чтобы нить оставалась натянутой. При этом карандаш будет вычерчивать на бумаге эллипс (рис. 23).

Теорема. Если плоскость сечения составляет некоторый угол с плоскостью основания цилиндра и не пересекает основания, то в сечении будет фигура, ограниченная эллипсом.

Доказательство. Рассмотрим цилиндрическую поверхность, составленную из образующих цилиндра и ее сечение плоскостью . Впишем в эту поверхность две сферы, касающиеся плоскости в некоторых точках F ₁ , F ₂ и цилиндрической поверхности по окружностям C ₁ , С₂ (рис. 24). Пусть A – произвольная точка сечения. Проведем через нее образующую и обозначим через А₁, А₂ точки пересечения этой образующей с окружностями C ₁ , C ₂ соответственно. Заметим, что прямая A ₁ A ₂ является касательной к обеим сферам. Воспользуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF ₁ = AA ₁ , AF ₂ = AA ₂ . Поэтому AF ₁ + AF₂ = AA₁ + AA₂ = A₁ A₂. Но длина отрезка А₁ А₂ есть расстояние между плоскостями окружностей C ₁ , C ₂ . Поэтому оно не зависит от выбора точки А сечения, т. е. является постоянной величиной. Значит, сечением цилиндрической поверхности является эллипс с фокусами F ₁ , F ₂ .

На рисунке 25 показано построение точек эллипса, получающегося как сечение боковой поверхности цилиндра плоскостью.

Для этого зададим два сопряженных диаметра AB и CD . Через точку A проведем образующую и выберем на ней какую-нибудь точку A ’ , принадлежащую сечению. Прямая A ’ O пересечет образующую, проходящую через точку B в некоторой точке B ’ , также принадлежащую сечению. Возьмем теперь на отрезке CD произвольную точку и проведем через нее прямую, параллельную A ’ B ’ . Ее точки пересечения с образующими цилиндра будут принадлежать сечению.

Рассмотрим еще одно свойство сечений цилиндра плоскостью, а именно, связь этих сечений с тригонометрическими функциями.

Возьмем прямоугольный лист бумаги и нарисуем на нем оси координат Ox и Oy параллельно соответствующим сторонам (рис. 26). Затем свернем этот лист в боковую поверхность прямого кругового цилиндра, радиус основания которого примем за единицу. Ось Ox свернется в окружность радиуса 1, а ось Oy станет образующей цилиндра (рис. 27). Через диаметр OD полученной окружности проведем сечение, составляющее с плоскостью окружности угол в 45 . В этом случае сечением будет эллипс.

Развернем цилиндр обратно в прямоугольник. При этом эллипс развернется в кривую, являющуюся частью синусоиды. Для доказательства этого из произвольной точки A на эллипсе опустим перпендикуляры на плоскость окружности и диаметр окружности OD . Получим соответственно точки B и C . Треугольник ABC прямоугольный и равнобедренный, так ABC = 90 ° , ACB = 45 ° . Следовательно, AB = BC . Заметим, что BC = sin x , где x — длина дуги OB . Для этого достаточно обратиться к рисунку 28 и вспомнить определение синуса. Таким образом, AB = sin x , где x = OB , т. е. эта кривая является частью синусоиды с уравнением y = sin x (рис. 29).

1. В каком случае сечением цилиндра плоскостью является круг?

Ответ: В случае, если плоскость сечения параллельна плоскости основания цилиндра.

2. Что будет сечением цилиндра плоскостью, проходящей через ось цилиндра?

3. Какую форму принимает поверхность воды в круглом наклоненном стакане?

4. Нарисуйте цилиндр и плоскость, пересекающую его боковую поверхность по эллипсу.

5. Может ли в сечении цилиндра плоскостью получиться: а) круг; б) прямоугольник; в) параллелограмм; г) трапеция д) треугольник?

Ответ: а), б) Да; в), г), д) нет.

6. Могут ли в сечениях цилиндра плоскостью получаться фигуры, отличные от круга, прямоугольника и эллипса?

Ответ: Да, если сечение пересекает боковую поверхность и основания цилиндра.

7. Используя карандаш, бумагу, нить и кнопки, нарисуйте эллипс.

8. Радиус основания цилиндра равен R . Плоскость сечения боковой поверхности цилиндра составляет с плоскостью основания угол j . Найдите малую и большую оси эллипса.

Ответ: R , .

9. Докажите, что сумма расстояний от любой точки эллипса до фокусов равна длине большой оси эллипса.

10. Докажите, что расстояния от концов малой оси эллипса до его фокусов равны половине большой оси.

11. Нарисуйте цилиндр и постройте несколько точек эллипса, получающегося в сечении его боковой поверхности плоскостью.

12. Докажите, что площадь эллипса, у которого большая и малая полуоси равны соответственно R , r , выражается формулой S = Rr . (Воспользуйтесь тем, что площадь ортогональной проекции фигуры равна произведению площади фигуры на косинус угла, образованного плоскостью фигуры и плоскостью ортогональной проекции.)

13. В основании цилиндра круг радиуса R . Боковая поверхность цилиндра пересечена плоскостью. Найдите площадь сечения цилиндра этой плоскостью, если она образует с плоскостью основания угол: а) 30 ° ; б) 45 ° ; в) 60 ° .

Ответ: а) ; б) ; в) .

14. Докажите, что если сечение цилиндра, свернутого из бумаги, проводить не под углом 45 ° , а под углом j , то уравнение соответствующей кривой будет иметь вид y = k · sin x , где k = tg j . Нарисуйте кривые соответствующие углам: а) j = 30 ° ; б) j = 60 ° .

15. Докажите, что если исходный прямоугольник свернуть в прямой круговой цилиндр не единичного, а некоторого другого радиуса a и произвести с этим цилиндром аналогичные операции, то получится кривая, задаваемая уравнением y = a · sin ( ).

16. Нарисуйте график функции: а) y = 2 sin ( ); б) y = sin 2 x .

17. Докажите, что если плоскость сечения проходит не через точку О, а через диаметр, образующий с О D (рис. 27) угол ₀, то получится кривая, задаваемая уравнением y = sin ( x — j ₀ ).

18. Нарисуйте график функции: а) y = sin ( x — ); б) y = sin ( x + ).

19. Возьмем прямоугольный лист бумаги с нарисованными на нем осями координат (рис. 26). Свернем этот лист в боковую поверхность правильной четырехугольной призмы (рис. 30). Сторону основания призмы примем за 1. Через точки О и D проведем сечение плоскостью, составляющей с плоскостью основания угол 45 ° . Развернем лист бумаги. Выясните, какая при этом получится кривая? Что изменится, если сечение проводить под другими углами?

Для данного конуса рассмотрим коническую поверхность, образованную прямыми, проходящими через вершину конуса и точки окружности основания конуса (рис. 31).

Сечения конической поверхности плоскостью можно рассматривать как центральную проекцию окружности основания конуса на эту плоскость. Поэтому, если плоскость параллельна плоскости основания и не проходит через вершину конуса, то в сечении конической поверхности получается окружность.

Исследуем другие возможные случаи сечения конической поверхности плоскостью, не проходящей через вершину конуса.

Теорема. Если плоскость образует с осью конуса угол, больший, чем угол между образующей и этой осью, то в сечении конической поверхности получается эллипс.

Доказательство. Докажем, что с умма расстояний от произвольной точки сечения до двух данных точек есть величина постоянная.

Впишем в коническую поверхность две сферы, касающиеся плоскости сечения в некоторых точках F ₁ , F ₂ и конической поверхности по окружностям C ₁ и C ₂ соответственно (рис. 32).

Пусть А – произвольная точка сечения. Проведем образующую AS и обозначим через А₁, А₂ точки ее пересечения с окружностями C ₁ , C ₂ соответственно. Заметим, что прямая AS является касательной к обеим сферам. Воспользуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF ₁ = AA ₁ , AF ₂ = AA ₂ . Поэтому AF ₁ + AF₂ = AA₁ + AA₂ = A₁ A₂. Но длина отрезка А₁ А₂ не зависит от выбора точки А сечения. Она равна образующей соответствующего усеченного конуса. Поэтому сумма расстояний от точки А до точек F ₁ , F ₂ будет постоянной.

На рисунке 33 показано построение точек эллипса, получающегося как сечение конуса плоскостью.

Для этого нужно зададим два сопряженных диаметра AB и CD . Выберем на образующих SA и SB точки A ’ и B ’ . Возьмем какую-нибудь точку O ₁ на диаметре AB , проведем через нее прямую, параллельную CD и найдем ее точки пересечения C ₁ и D ₁ с окружностью основания конуса. Соединим точки O ₁ , C ₁ , D ₁ с вершиной конуса. Через точку O ’ ₁ пересечения O ₁ S с A ’ B ’ проведем прямую, параллельную C ₁ D ₁ и найдем ее точки пересечения с C ₁ S и D ₁ S . Полученные точки будут принадлежать сечению.

Теорема. Если плоскость образует с осью конуса угол, равный углу между образующей и этой осью, то в сечении конической поверхности получается парабола.

Доказательство. Напомним, что параболой называется геометрическое место точек плоскости, равноудаленных от данной точки F , называемой фокусом, и данной прямой d , называемой директрисой, лежащих в этой плоскости.

Впишем в коническую поверхность сферу, касающуюся плоскости a в некоторой точке F и конической поверхности по окружности C , лежащей в плоскости b , перпендикулярной оси. Плоскости a и b образуют между собой угол 90 ° — j и пересекаются по некоторой прямой d (рис. 34).

Пусть А — произвольная точка сечения. Проведем образующую AS и обозначим через А₁ точку ее пересечения с окружностью C . Заметим, что прямая AS является касательной к сфере. Прямая AF также является касательной. Отрезки А F и АА₁ равны как отрезки касательных, проведенных к сфере из одной точки.

Опустим из точки А перпендикуляр АВ на плоскость b и перпендикуляр А D на прямую d . Угол А₁ АВ равен j . Угол А D В является углом между плоскостями a и b и поэтому равен 90 ° — j . Следовательно, угол BAD равен j .

Прямоугольные треугольники АВА₁ и АВ D равны, так как имеют общий катет и соответственно равные углы. Поэтому АА₁ = А D . Окончательно получаем равенство AF = AD , которое означает, что расстояние от произвольной точки сечения до точки F равно расстоянию от этой точки до прямой d , т. е. сечением конической поверхности в этом случае является парабола.

На рисунке 35 показано построение точек параболы, получающейся как сечение конуса плоскостью.

Теорема. Если плоскость образует с осью конуса угол, меньший угла между образующей и этой осью, то в сечении конической поверхности получается гипербола.

Доказательство. Напомним, что гиперболой называется геометрическое место точек на плоскости, модуль разности расстояний от которых до двух заданных точек плоскости постоянен.

Впишем в коническую поверхность сферы, касающиеся плоскости сечения в некоторых точках F ₁ и F ₂ и конической поверхности по окружностям C ₁ и C ₂ соответственно.

Пусть А — точка сечения, расположенная в той же части конической поверхности, что и точка F ₁ (рис. 36). Проведем образующую AS и обозначим через А₁, А₂ точки ее пересечения с окружностями C₁, C₂ соответственно. Воспользуемся тем, что отрезки касательных, проведенных к сфере из одной точки, равны. Тогда AF₁ = AA₁, AF₂ = AA₂. Поэтому AF ₂ — AF₁ = AA₂ — AA₁ = A₁ A₂. Но длина отрезка А₁ А₂ не зависит от выбора точки А сечения. Она равна сумме образующих соответствующих конусов. Следовательно, разность AF₂ — AF₁ расстояний от точки А до точек F₁, F₂ будет постоянной. Аналогичным образом показывается, что если точка A расположена в той же части конической поверхности, что и точка F ₂ , то разность AF₁ – AF₂ будет постоянной. Таким образом, сечением конической поверхности в этом случае является гипербола.

На рисунке 37 показано построение точек гиперболы, получающейся как сечение конуса плоскостью.

Конические сечения с древних времен привлекали к себе внимание ученых. Так древнегреческий ученый Менехм ( IV в. до н. э.) пользовался параболой и гиперболой для решения знаменитой задачи удвоения куба. Исследовали свойства конических сечений Евклид ( IV в. до н. э.) и Архимед ( III в. до н. э.). Полное и систематическое учение об этих кривых было изложено Аполлонием Пергским ( III — II вв. до н. э.) в восьмитомном труде «Конические сечения». Там он впервые показал, как можно получить эти кривые, рассекая один и тот же конус плоскостью под разными углами. Он же ввел термины «эллипс», «парабола» и «гипербола», означающие в переводе с греческого соответственно «недостаток», «приложение» и «избыток». Происхождение этих названий связано с задачей построения прямоугольника с заданным основанием, равновеликого данному квадрату. Переводя с геометрического языка, которым пользовался Аполлоний, на современный алгебраический язык, получаем уравнение

y 2 = 2 px + lx 2 ,

где эллипсу соответствует отрицательное, гиперболе – положительное, а параболе – равное нулю значение второго члена в правой части. Таким образом, для параболы площадь квадрата, построенного на ординате y , равна площади прямоугольника со сторонами 2 p и x . Для эллипса площадь прямоугольника меньше, а для гиперболы — больше площади соответствующего квадрата.

Интерес к коническим сечениям особенно возрос после того, как Г. Галилей (1564-1642) установил, что тело, брошенное под углом к горизонту, двигается по параболе, а И. Кеплер сформулировал законы движения планет, согласно которым они описывают эллипсы. Позднее было установлено, что кометы и другие небесные тела движутся по эллипсам, параболам или гиперболам в зависимости от их начальной скорости.

Так, если скорость космического корабля при выходе на орбиту Земли составляет 7,9-11,1 км/с (первая космическая скорость), то он будет двигаться вокруг Земли по эллиптической орбите.

Если его скорость составляет 11,2-16,7 км/с (вторая космическая скорость), то он будет двигаться по параболической орбите и покинет зону земного притяжения. Однако он не сможет выйти за пределы Солнечной системы.

Если же его скорость больше 16,7 км/с (третья космическая скорость), то он будет двигаться по гиперболической орбите и уйдет за пределы Солнечной системы.

1. В каком случае сечением конуса плоскостью является круг?

Ответ: В случае, если плоскость сечения параллельна плоскости основания конуса.

2. Что будет сечением конуса плоскостью, проходящей через ось конуса?

3. Может ли в сечении конуса плоскостью получиться: а) круг; б) треугольник, в) прямоугольник?

Ответ: а), б) Да; в) нет.

4. Могут ли в сечениях боковой поверхности конуса плоскостью получаться фигуры, отличные от окружности, эллипса, параболы, гиперболы?

Ответ: Да, если сечение проходит через вершину конуса.

5. Какой фигурой является сечение конуса плоскостью, проходящей через его вершину?

Ответ: Равнобедренный треугольник.

6. Какую форму принимает поверхность воды в наклоненной конусообразной колбе?

Ответ: В зависимости от угла наклона будет эллипс, парабола или гипербола.

7. Пучок света карманного фонарика имеет форму конуса. Какую форму имеет освещенный фонариком участок ровной поверхности в зависимости от угла наклона фонарика?

Ответ: Эллипс, парабола или гипербола.

8. Может ли центральная проекция сферы быть фигурой, ограниченной: а) окружностью; б) эллипсом; в) параболой; г) гиперболой?

Ответ: а), б), в) г) Да.

9. Через центр основания конуса и середину образующей проведена плоскость. Что представляет собой сечение конуса этой плоскостью?

Ответ: Фигура, ограниченная параболой.

10. Высота конуса равна радиусу основания. Что представляет собой сечение конуса плоскостью, образующей с осью угол: а) 30 ° ; б) 45 ° ; в) 60 ° ?

Ответ: Фигура, ограниченная а) гиперболой; б) параболой; в) эллипсом.

11. Образующая конуса в два раза больше радиуса основания. Под каким углом к оси нужно провести сечение конуса плоскостью, чтобы в сечении конической поверхности получить: а) эллипс; б) параболу; в) гиперболу?

Ответ: а) Больше 60 ° ; б) 60 ° ; в) меньше 60 ° .

12. Осевое сечение конуса – равносторонний треугольник со стороной, равной единице. Через середину образующей проведено сечение конуса плоскостью, перпендикулярной этой образующей. Найдите площадь сечения.

Ответ: .