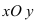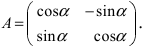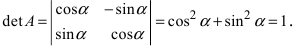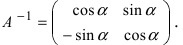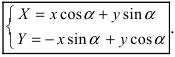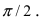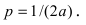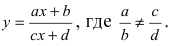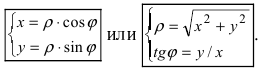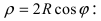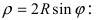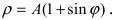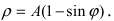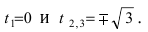Как повернуть систему координат на вектор

Пришлось это мне в последнее время поработать с задачами, где нужно было оперировать кватернионами и заниматься перепроецированием векторов в разные системы координат (это еще называется заменой базиса). Сначала по чужим формулам — причем с опечатками и даже, как выяснилось, с фактическими ошибками — а потом делать свои, по аналогии. И всё даже работало! Но сохранялся какой-то туман в понимании происходящего. А всё, как оказалось, из-за этих ошибок: их комбинация давала систему, в целом сохраняющую корректность, неверным путем таки достигался верный результат. Зато такая удача сильно мешала осознанию проблемы и прояснению природы феномена «верный итог при подозрительных формулах». При этом разбираться досконально времени все не было — работает же, числа выдает правильные, чего тебе еще надо, собака? Вперед, нужно больше золота кода! А вот сейчас пришел момент, когда я, похоже, окончательно всё понял, и хочу поделиться получившейся картинкой с окружающими. Вдруг кому пригодится, и себе памятка.

Заранее оговорюсь, что материал не претендует на академичность изложения, а скорее просто описывает удобный для запоминания способ интерпретации того, что происходит при перепроецировании векторов.

Стало быть, речь у нас пойдет в особенности о проекциях и поворотах.

Видео:Координаты вектора. 9 класс.Скачать

Исходные посылки

Описание кватернионов и матриц поворота как таковых опущу, предполагаю, что читатели знакомы с ними. Вектор здесь будет пониматься в его интуитивном представлении, как отрезок прямой в трехмерном пространстве, имеющий длину и направление. Исходное положение вектора будет иметь индекс «–», конечное — индекс «+».

Кватернионы и матрицы поворота могут быть использованы как для выполнения пространственного поворота векторов, так и для описания взаимной ориентации систем координат. В частности, для описания положения целевой системы координат относительно исходной: как нужно повернуть исходную, чтобы ее оси совпали с одноименными осями целевой. Матрица поворота (она же матрица ориентации, для случая описания взаимной ориентации систем координат) может быть получена из нормированного кватерниона ориентации по известным из литературы формулам. Обратное тоже верно: можно получить кватернион ориентации из матрицы.

Вектор , подлежащий повороту, задается величинами его проекций (длинами проекций) на оси исходной системы координат: три числа – проекции на три ортогональных оси . Получается матрица-столбец размерности 3х1, которая также называется вектором. Чтобы не смешивать в тексте подобную запись проекций вектора с интуитивным представлением о нем, я буду и дальше называть эту запись «матрицей-столбцом».

Видео:Координаты точки и координаты вектора 1.Скачать

Поворот вектора

Поворачивать вектор можно, как уже сказано, и с помощью матрицы, и с помощью кватерниона.

Поворот с использованием матрицы: матрица поворота умножается на исходную матрицу-столбец. На выходе имеем другую, результирующую матрицу-столбец:

Поворот с использованием кватерниона ориентации выполняется в два шага:

1. Из исходной матрицы-столбца и кватерниона вычисляется промежуточная матрица-столбец , где – операция векторного произведения векторов;
2. Вычисляется значение результирующей матрицы-столбца по формуле

Числа в результирующей матрице-столбце, полученной любым из этих способов — это проекции вектора в его новом, повернутом положении, на оси все той же исходной системы координат.

С поворотом вектора дело ясное, вопросов нет.

Видео:§35 Формулы поворота координатных осейСкачать

Перепроецирование вектора

А вот задача перепроецирования вектора из одной системы координат в другую несколько контринтуитивна. Формулировка задачи: необходимо узнать, как некоторый вектор, заданный в исходной системе координат, выглядит в целевой системе. Иначе говоря, по проекциям вектора на оси исходной системы узнать проекции вектора на оси целевой. При этом задан кватернион или матрица ориентации целевой системы относительно исходной.

Может показаться, что для решения этой задачи нужно просто повернуть вектор из исходной системы координат в целевую, пользуясь кватернионом или матрицей ориентации второй относительно первой. Однако это не так! Выполнив подобную операцию, мы узнаем только, как новый, повернутый вектор выглядит в осях все той же исходной системы, а это не то, что нас интересует .

Важно, однако, обратить внимание на то, что после проведения подобного поворота сам вектор окажется ориентирован относительно целевой системы координат так же, как он был до операции ориентирован относительно исходной. В этом кроется ключ к правильному ходу действий. Для получения проекций интересующего нас вектора на целевую систему координат нужно выполнить операцию «в обратную сторону»:

1. Задать в целевой системе координат «временный» вектор с теми же величинами проекций на оси этой целевой системы, какие есть у интересующего нас («заданного») вектора на оси исходной системы. Таким образом, «временный» вектор будет ориентирован относительно целевой системы так же, как заданный вектор ориентирован относительно исходной;
2. Определить ориентацию исходной системы относительно целевой. Здесь легко: нужная ориентация описывается либо кватернионом, сопряженным к имеющемуся (), либо матрицей , обратной по отношению к имеющейся; причем для матрицы ориентации, чей определитель всегда равен 1, обратная матрица совпадает с транспонированной , поэтому достаточно транспонировать имеющуюся матрицу ориентации;
3. Повернуть «временный» вектор с использованием полученного кватерниона/матрицы. Вектор повернется относительно целевой системы координат так же, как относительно нее повернута исходная система. При этом, в силу всего сказанного ранее, а) «временный» вектор станет ориентирован уже относительно исходной системы так, как был ранее ориентирован относительно целевой, и, следовательно, точно совпадет с заданным вектором, и б) результатом операции будет матрица-столбец, описывающая, как теперь «временный» (а значит, и заданный) вектор выглядит в осях целевой системы координат.

Ура, это именно то, что нам нужно!

Кроме того, быстро становится очевидно, что с точки зрения реализации никакой «временный» вектор (в смысле «матрица-столбец») на самом деле не нужен: в ходе операции он никак не модифицируется, и при этом численно является копией исходного вектора. Так что, разумеется, можно спокойно брать сам исходный вектор и проводить операции с ним. Описание выше лишь подробнее иллюстрирует смысл происходящего.

Видео:Как построить точки в системе координат OXYZСкачать

Преобразования декартовой системы координат с примерами решения

Содержание:

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Преобразования декартовой системы координат

Параллельный перенос и поворот системы координат

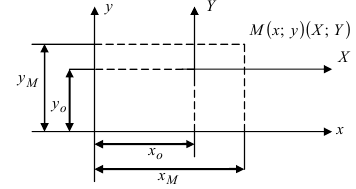
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):

Рис. 46. Параллельный перенос одной системы координат относительно другой системы.

Систему координат

Пример:

Дана точка М(3;2) и начало новой системы координат 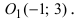Вычислить положение точки М в новой системе отсчета.

Решение:

Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим 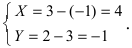Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).

2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 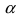(Рис. 47):

Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.

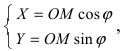
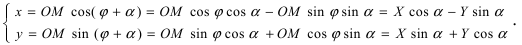
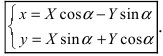
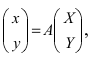
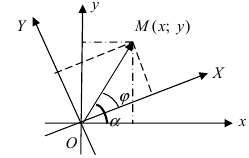
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода

Найдем обратное преобразование системы координат, найдем матрицу 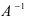обратную к матрице А:

Найдем алгебраические дополнения всех элементов

Запишем обратную матрицу

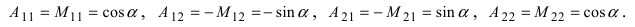
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.

Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.

Таким образом, имеем 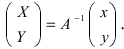Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:

Пример:

Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол

Решение:

Воспользуемся полученными формулами 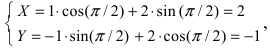т.е. в новой системе координат точка имеет координаты М(2; -1).

Рассмотрим применение преобразования координат:

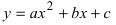
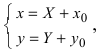
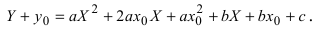
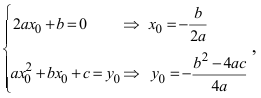
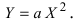
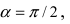
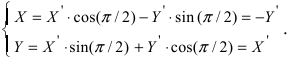
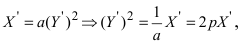
а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы

Пример:

Преобразовать уравнение параболы 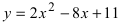к каноническому виду.

Решение:

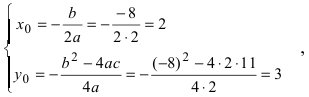
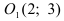
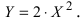
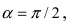
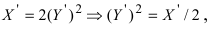
Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка — начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда

следовательно, параметр параболы р = 1/4.

б) Выяснить, какую кривую описывает функция

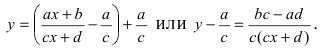
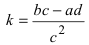
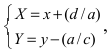
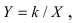
Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение

и новые координаты получим уравнение которое описывает равнобочную гиперболу.

Полярные координаты. Замечательные кривые

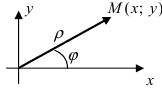
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 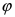между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).

Рис. 48. Полярная система координат.

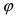
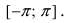
Главными значениями угла являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами

Рассмотрим замечательные кривые в полярной системе координат:

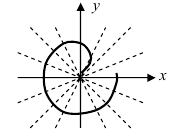
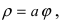
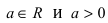
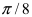
1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.

Рис. 49. Спираль (улитка) Архимеда.

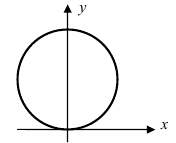
2. Уравнение окружности: уравнение 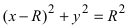описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид

Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.

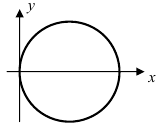
3. Уравнение 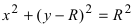описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид

Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.

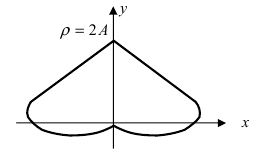
4. Кардиоиды:

Рис. 52. Кардиоида

Рис. 53. Кардиоида

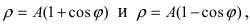
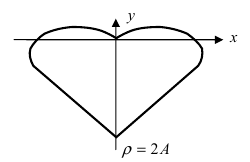
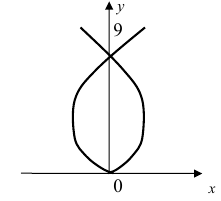
Аналогично выглядят кардиоиды но они вытянуты вдоль оси абсцисс Ох.

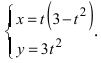
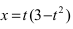
5. Петля: Величина равна нулю при

Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид

• Бесконечно малые и бесконечно большие функции
• Замечательные пределы
• Непрерывность функций и точки разрыва
• Точки разрыва и их классификация
• Экстремум функции
• Методы решения систем линейных алгебраических уравнений (СЛАУ)
• Скалярное произведение и его свойства
• Векторное и смешанное произведения векторов

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Матрица поворотаСкачать

Матрицы поворота, углы Эйлера и кватернионы (Rotation matrices, Euler angles and quaternions)

Объект обычно определяется в удобной для его описания локальной системе координат (ЛСК), а его положение в пространстве — в глобальной системе координат (ГСК).

В трёхмерном пространстве переход из одной СК в другую описывается в общем случае системой линейных уравнений:

Уравнения могут быть записаны через матрицы аффинных преобразований в однородных координатах одним из 2-х способов:

В ортогональных СК оси X, Y и Z взаимно перпендикулярны и расположены по правилу правой руки:

На рисунке справа большой палец определяет направление оси, остальные пальцы — положительное направление вращения относительно этой оси.

Все три вектора направлений есть единичными.

Ниже приводится единичная матрица для 2-х способов записи уравнений геометрических преобразований. Такая матрица не описывает ни перемещения, ни вращения. Оси ЛСК и ГСК совпадают.

Далее рассматривается матрица для второго способа матричной записи уравнений (матрица справа). Этот способ встречается в статьях значительно чаще.

При использовании матрицы вы можете игнорировать нижнюю строку. В ней всегда хранятся одни и те же значения 0, 0, 0, 1. Она добавлена для того, чтобы мы могли перемножать матрицы (напомню правило перемножения матриц и отмечу, что всегда можно перемножать квадратные матрицы). Подробнее см. Композиция матриц. Однородные координаты.

Остальные 12 значений определяют координатную систему. Первый столбец описывает компоненты направления оси X(1,0,0). Второй столбец задает направление оси Y(0,1,0), третий – оси Z (0,0,1). Последний столбец определяет положение начала системы координат (0,0,0).

Как будет выглядеть матрица Евклидового преобразования (преобразование движения) для задания ЛСК , с началом в точке (10,5,0) и повёрнутой на 45° вокруг оси Z глобальной СК, показано на рисунке.

Рассмотрим сначала ось X. Если новая система координат повернута на 45° вокруг оси z, значит и ось x повернута относительно базовой оси X на 45° в положительном направлении отсчета углов. Таким образом, ось X направлена вдоль вектора (1, 1, 0), но поскольку вектор системы координат должен быть единичным, то результат должен выглядеть так (0.707, 0.707, 0). Соответственно, ось Y имеет отрицательную компоненту по X и положительную по Y и будет выглядеть следующим образом (-0.707, 0.707, 0). Ось Z направления не меняет (0, 0, 1). Наконец, в четвертом столбце вписываются координаты точки начала системы координат (10, 5, 0).

Частным случаем матриц геометрических преобразований есть матрицы поворота ЛСК относительно базовых осей ГСК. Вектора осей ЛСК здесь выражены через синусы и косинусы углов вращения относительно оси, перпендикулярной к плоскости вращения.

От матрицы преобразований размером 4*4 можно перейти непосредственно к матрице поворота 3*3, убрав нижний ряд и правый столбец. При этом, система линейных уравнений записывается без свободных элементов (лямда, мю, ню), которые определяют перемещение вдоль осей координат.

Путем перемножения базовых матриц можно получать комбинированные вращения. Ниже рассмотрены возможности комбинировать вращениями через матрицы поворота на примерах работы с углами Эйлера.

Видео:Перенос объектов в новую систему координат. AutoCADСкачать

Матрицы поворота и углы Эйлера

От выбора осей и последовательности вращения зависит конечный результат. На рисунках отображена следующая последовательность вращения относительно осей ЛСК:

• оси Z (угол alpha);
• оси X (угол beta);
• оси Z (угол gamma).

Получил от читателя этой статьи вопрос: «Как понять, из каких углов поворота вокруг осей X,Y,Z можно получить текущее положение объекта, когда в качестве задания мы уже имеем повернутый объект, а нужно вывести его в это положение, последовательно повернув его из какого-то начального положения до полного совмещения с заданным?»

Мой ответ: «Если я правильно понял вопрос, то Вас интересует, как от начального положения перейти к заданному положению объекта, используя для этого элементарные базовые аффинные преобразования.

Начну с аналогии. Это как в шахматах. Мы знаем как ходит конь. Необходимо переместить его в результате многоходовки в нужную клетку на доске — при условии, что это возможно.

Подробно эта проблематика рассмотрена в статье Преобразование координат при калибровке роботов.

Умение правильно выбирать последовательность элементарных геометрических преобразований помогает в решении множества других задач (см. Примеры геометрических преобразований).»

Можно получить результирующую матрицу, которая определяет положение ГСК относительно ЛСК. Для этого необходимо перемножить матрицы с отрицательными углами в последовательности выполнения поворотов:

Почему знак угла поворота меняется на противоположный? Объяснение этому простое. Движение относительно. Абстрагируемся и представим, что ГСК меняет положение относительно неподвижной ЛСК. При этом направление вращения меняется на противоположное.

Перемножение матриц даст следующий результат:

Результирующую матрицу можно использовать для пересчета координат из ГСК в ЛСК:

Для пересчета координат из ЛСК в ГСК используется результирующая обратная матрица.

В обратной матрице последовательность поворота и знаки углов меняются на противоположные (в рассматриваемом примере снова на положительные) по сравнению с матрицей определения положения ГСК относительно ЛСК.

Перемножение матриц даст следующий результат:

Выше был рассмотрен случай определения углов Эйлера через вращение относительно осей ЛСК. То же взаимное положение СК можно получить, выполняя вращение относительно осей ГСК:

• оси z (угол (gamma+pi/2));
• оси y (угол угол beta);
• оси z (угол (-alpha)).

Определение углов Эйлера через вращение относительно осей ГСК позволяет также просто получить зависимости для пересчета координат из ЛСК в ГСК через перемножение матриц поворота.

В рамках рассматриваемой задачи вместо угла gamma в матрицe Az используем угол gamma+pi/2.

Также легко можно перейти к зависимостям для пересчета координат из ГСК в ЛСК.

Обратная матрица получается перемножением обратных матриц в обратном порядке по сравнению с прямым преобразованием. При этом каждая из обратных матриц вращения может быть получена заменой знака угла на противоположный.

Детально с теоретическими основами аффинных преобразований (включая и вращение) можно ознакомиться в статье Геометрические преобразования в графических приложениях

Примеры преобразований рассмотрены в статьях:

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Axis Angle представление вращения

Выбрав подходящую ось (англ. rotation axis) и угол (англ. rotation angle) можно задать любую ориентацию объекта.

Обычно хранят ось вращения в виде единичного вектора и угол поворота вокруг этой оси в радианах или градусах.

q = [ x, y, z, w ] = [ v, w ]

В некоторых случаях удобно хранить угол вращения и ось в одном векторе. Направление вектора при этом совпадает с направлением оси вращения, а его длина равна углу поворота:

q = [ x, y, z]; w=sqrt (x*x +y*y +z*z)

В физике, таким образом хранят угловую скорость. Направление вектора совпадает с направлением оси вращения, а длина вектора равна скорости (в радианах в секунду).

Можно описать рассмотренные выше углы Эйлера через Axis Angle представление в 3 этапа:

q1 = [ 0, 0, 1, alpha]; q2 = [ 1, 0, 0, beta]; q3 = [ 0, 0, 1, gamma ]

Здесь каждое вращение выполняется относительно осей текущего положения ЛСК. Такое преобразование равнозначно рассмотренному выше преобразованию через матрицы поворота:

Возникает вопрос, а можно ли 3 этапа Axis Angle представления объединить в одно, подобно матрицам поворота? Попробуем решить геометрическую задачу по определению координат последнего вектора вращения в последовательности преобразований через Axis Angle представления:

q = [ x, y, z, gamma ]

Есть ли представление q= [x, y, z, gamma] композицией последовательности из 3-х этапов преобразований? Нет! Координаты x, y, z определяют всего лишь положение оси Z ЛСК после первого и второго этапов преобразований:

При этом ось Z, отнюдь, не есть вектор вращения для Axis Angle представления, которое могло бы заменить рассмотренные 3-х этапа преобразований.

Еще раз сформулирую задачу, которая математически пока не решена: «Необходимо найти значение угла (rotation angle) и положение оси (rotation axis), вращением относительно которой на этот угол можно заменить комбинацию из 3-х поворотов Эйлера вокруг осей координат».

К сожалению, никакие операции (типа объединения нескольких преобразований в одно) с Axis Angle представлениями нельзя выполнить. Не будем расстраиваться. Это можно сделать через кватернионы, которые также определяют вращение через параметры оси и угол.

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Кватернионы

Кватернион (как это и видно по названию) представляет собой набор из четырёх параметров, которые определяют вектор и угол вращения вокруг этого вектора. По сути такое определение ничем не отличается от Axis Angle представления вращения. Отличия лишь в способе представления. Как же хранят вращение в кватернионе?

q = [ V*sin(alpha/2), cos(alpha/2) ]

В кватернионе параметры единичного вектора умножается на синус половины угла поворота. Четвертый компонент — косинус половины угла поворота.

Таблица с примерами значений кватернионов:

Представление вращения кватернионом кажется необычным по сравнению с Axis Angle представлением. Почему параметры вектора умножаются на синус половины угла вращения, четвертый параметр — косинус половины угла вращения, а не просто угол?

Откуда получено такое необычное представление кватерниона детально можно ознакомиться в статье Доступно о кватернионах и их преимуществах. Хотя программисту не обязательно знать эти детали, точно также как и знать, каким образом получены матрицы преобразования пространства. Достаточно лишь знать основные операции с кватернионами, их смысл и правила применения.

Видео:№917. Начертите прямоугольную систему координат Оху и координатные векторы i и j. ПостройтеСкачать

Основные операции над кватернионами

Кватернион удобно рассматривать как 4d вектор, и некоторые операции с ним выполняются как над векторами.

Видео:9 класс, 2 урок, Координаты вектораСкачать

Сложение, вычитание и умножение на скаляр.

Смысл операции сложения можно описать как «смесь» вращений, т.е. мы получим вращение, которое находится между q и q’.

Что-то подобное сложению кватернионов выполнялось при неудачной попытке объединить 3 этапа Axis Angle представления.

Умножение на скаляр на вращении не отражается. Кватернион, умноженный на скаляр, представляет то же самое вращение, кроме случая умножения на 0. При умножении на 0 мы получим «неопределенное» вращение.

Пример сложения 2-х кватернионов:

Видео:Видеоурок по AutoCAD: поворот осей координат и вида на чертёжСкачать

Норма и модуль

Следует различать (а путают их часто) эти две операции:

Модуль (magnitude), или как иногда говорят «длина» кватерниона:

Через модуль кватернион можно нормализовать. Нормализация кватерниона — это приведение к длине = 1 (так же как и в векторах):

Видео:Прямоугольная система координат в пространстве. Координаты вектора. Видеоурок по геометрии 11 классСкачать

Обратный кватернион или сопряжение ( conjugate )

Обратный кватернион задает вращение, обратное данному. Чтобы получить обратный кватернион достаточно развернуть вектор оси в другую сторону и при необходимости нормализовать кватернион.

Например, если разворот вокруг оси Y на 90 градусов = (w=0,707; x = 0; y = 0,707; z=0), то обратный = (w=0,707; x = 0; y = -0,707; z=0).

Казалось бы, можно инвертировать только компоненту W, но при поворотах на 180 кватернион представляется как (w=1; x = 0; y = 0; z=0), то есть, у него длина вектора оси = 0.

Фрагмент программной реализации:

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Инверсный (inverse) кватернион

Существует такой кватернион, при умножении на который произведение дает нулевое вращение и соответствующее тождественному кватерниону (identity quaternion), и определяется как:

Видео:Как изменить систему координат: AutoCAD #5Скачать

Тождественный кватернион

Записывается как q[0, 0, 0, 1]. Он описывает нулевой поворот (по аналогии с единичной матрицей), и не изменяет другой кватернион при умножении.

Видео:11 класс, 2 урок, Координаты вектораСкачать

Скалярное произведение

Скалярное произведение полезно тем, что дает косинус половины угла между двумя кватернионами, умноженный на их длину. Соответственно, скалярное произведение двух единичных кватернионов даст косинус половины угла между двумя ориентациями. Угол между кватернионами — это угол поворота из q в q’ (по кратчайшей дуге).

Видео:Полярная система координатСкачать

Вращение 3d вектора

Вращение 3d вектора v кватернионом q определяется как

причем вектор конвертируется в кватернион как

и кватернион обратно в вектор как

Видео:Координаты в Автокад. Система координат в AutoCADСкачать

Умножение кватернионов

Одна из самых полезных операций, она аналогична умножению двух матриц поворота. Итоговый кватернион представляет собой комбинацию вращений — сначала объект повернули на q, а затем на q’ (если смотреть из глобальной системы координат).

Примеры векторного и скалярного перемножения 2-х векторов векторное произведение — вектор: Скалярное произведение — число:

Пример умножения 2-х кватернионов:

Видео:Видеоурок "Преобразование координат"Скачать

Конвертирование между кватернионом и Axis Angle представлением

В разделе Axis Angle представление вращения была сделана неудачная попытка объединить 3 Axis Angle представления в одно . Это можно сделать опосредовано. Сначала Axis Angle представления конвертируются в кватернионы, затем кватернионы перемножаются и результат конвертируется в Axis Angle представление.

Пример конвертирования произведения 2-х кватернионов в Axis Angle представление:

Фрагмент программы на C:

Видео:5 4 Координаты Преобразование координат при замене базисаСкачать

Конвертирование кватерниона в матрицу поворота

Матрица поворота выражается через компоненты кватерниона следующим способом:

где

Проверим формулы конвертирования на примере конвертирования произведения 2-х кватернионов в матрицу поворотов:

Определяем элемент матрицы m[0][0] через параметры кватерниона:

Соответствующее произведению кватернионов (q1 и q2) произведение матриц поворотов было получено ранее (см. Матрицы поворота и углы Эйлера):

Как видим, результат m[0][0], полученный через конвертирование, совпал с значением в матрице поворота.

Фрагмент программного кода на С для конвертирования кватерниона в матрицу поворота:

При конвертировании используется только умножения и сложения, что является несомненным преимуществом на современных процессорах.

Часто для задания вращений используют только кватернионы единичной длины, но это не обязательно и иногда даже не эффективно. Разница между конвертированием единичного и неединичного кватернионов составляет около 6-ти умножений и 3-х сложений, зато избавит во многих случаях от необходимости нормировать (приводить длину к 1) кватернион. Если кусок кода критичен по скорости и вы пользуетесь только кватернионами единичной длины тогда можно воспользоваться фактом что норма его равна 1.

Конвертирование матрицы поворота в кватернион

Конвертирование матрицы в кватернион выполняется не менее эффективно, чем кватерниона в матрицу, но в итоге мы получим кватернион неединичной длины. Его можно нормализовать.

Фрагмент программного кода конвертирования матрицы поворота в кватернион: