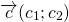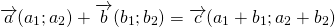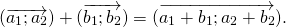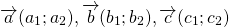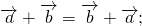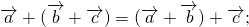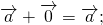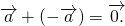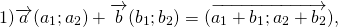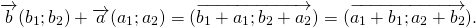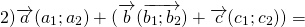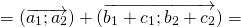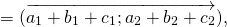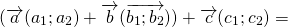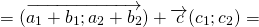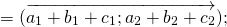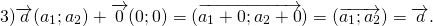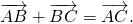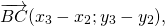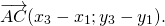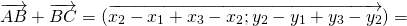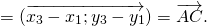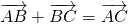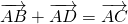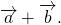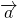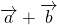Как построить треугольник по векторам

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Онлайн калькулятор. Площадь треугольника построенного на векторах.

Этот онлайн калькулятор позволит вам очень просто найти площадь треугольника построенного на векторах.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади треугольника построенного на векторах и закрепить пройденый материал.

Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

Калькулятор для вычисления площади треугольника построенного на векторах

Выберите каким образом задается треугольник:

Введите значения векторов: Введите координаты точек:

Инструкция использования калькулятора для вычисления площади треугольника построенного на векторах

Ввод данных в калькулятор для вычисления площади треугольника построенного на векторах

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления площади треугольника построенного на векторах

• Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Теория. Площадь треугольника построенного на векторах

Определение Площадь треугольника образованного векторами a и b равна половине модуля векторного произведения этих векторов:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Урок 4. Векторы. Сложение векторов. Правило треугольника. Правило параллелограмма.Скачать

Площадь треугольника, построенного на векторах: онлайн-калькулятор

Формула площади треугольника заложена в программе и вычисляет половину модуля векторного произведения:

Чтобы найти площадь треугольника, необходимы задать значения двух векторов или координаты вершин треугольника. После этого вы получите готовое решение с пояснениями и ответ. Сервис используют школьники, их родители, студенты, преподаватели.

1. Выберите форму представления треугольника «Двумя векторами сторон».
   
2. Введите значения векторов a и b в соответствующие поля. Отправьте задание на решение кнопкой «Рассчитать»
   
3. Получите решение и ответ.
   
   

1. Выберите форму представления треугольника «Координатами точек».
   
2. Введите координаты вершин A, B, C в соответствующие поля. Отправьте задание на решение кнопкой «Рассчитать».
   
   
3. Получите решение и ответ.
   
   
   

Видео:Угол между диагоналями куба. Метод координат и векторов. Задачи на даче-15.Скачать

Материалы, которые помогут вам лучше разобраться в теме:

Видео:Площадь треугольника, построенного на векторахСкачать

Как найти площадь треугольника, построенного на векторах

Онлайн-калькулятор позволяет учащимся готовиться к занятиям, разбираться в непонятной теме, тренироваться на примерах. Расчеты производятся бесплатно, поэтому вы сможете сэкономить деньги на репетиторе и самостоятельно осваивать материал. Моментальное решение также поможет сдать зачет или экзамен, написать контрольную на хорошую оценку. Родители смогут быстро проверить домашнее задание ребенка, а преподаватели – автоматизировать процесс создания обучающих материалов.

Чтобы вычислить площадь треугольника через векторы, программа выполняет следующие действия:

• Анализирует введенные данные. Если указаны координаты точек, рассчитываются векторы a и b.
• Находит произведение векторов.
• Вычисляет модуль вектора.
• Делит результат на 2 и выдает ответ.

С помощью нашего сайта вы сможете изучить, как найти площадь треугольника не только по векторам, но и другими способами. Мы разделили калькуляторы по темам для удобного использования. Так вы быстро найдете нужную тему и получите правильный ответ. В автоматических расчетах исключена потеря данных между действиями, опечатки. Благодаря калькулятору вы сможете сравнить решение с собственным и найти ошибку.

Видео:Вычитание векторов. 9 класс.Скачать

Построение векторов в треугольник

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Сложение векторов

Сумма векторов

Свойства сложения векторов:

Для любых векторов

3) свойство прибавления нулевого вектора:

4) сумма противоположных векторов равна нулевому вектору:

Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:

Так как соответствующие координаты равны, то эти векторы равны.

(О сложении векторов)

Каковы бы ни были точки A, B, C, имеет место векторное равенство:

Что и требовалось доказать.

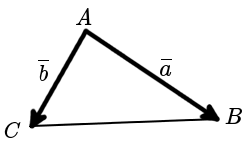
Правило треугольника построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.

Например,

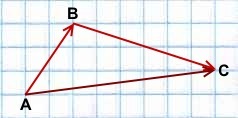
(то есть это правило следует из теоремы о сложении векторов).

Правило параллелограмма построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.

Например,

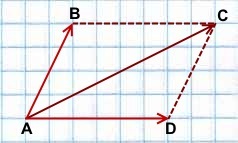
Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.

При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.

Построить сумму векторов

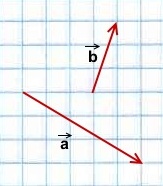
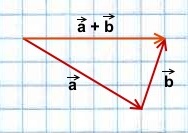
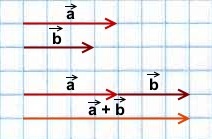
1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора

Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).

2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы

от общего начала.

Достроим на этих векторах параллелограмм.

Сумма

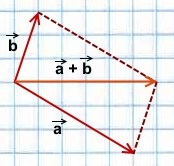
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.

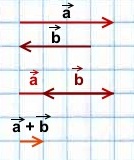
1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.

2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.

Фактически в обоих случаях мы используем правило треугольника сложения векторов:

от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.

Из неравенства треугольника следует ещё два свойства сложения векторов:

Видео:Сложение векторов. 9 класс.Скачать

Сумма и разность векторов

В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.

Видео:Построить разность векторов.Скачать

Сумма векторов

Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:

Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .

Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.

Формула сложения векторов

Элементы вектора c равняются попарной сумме соответствующих элементов a и b .

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a + b = x + b_x; a_y + b_y> » data-order=» a + b = x + b_x; a_y + b_y> » style=»min-width:55.0847%; width:55.0847%;»> a + b = x + b_x; a_y + b_y>

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a + b = x + b_x; a_y + b_y; a_z + b_z> » data-order=» a + b = x + b_x; a_y + b_y; a_z + b_z> «> a + b = x + b_x; a_y + b_y; a_z + b_z>

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a + b = 1 + b₁; a₂ + b₂; . a_n + b_n> » data-order=» a + b = 1 + b₁; a₂ + b₂; . a_n + b_n> «> a + b = 1 + b₁; a₂ + b₂; . a_n + b_n>

Свойства сложения векторов

1. Коммутативность: a + b = b + a

2. Ассоциативность: ( a + b ) + c = a + ( b + c )

3. Прибавление к нулю: a + 0 = a

4. Сумма противоположных векторов: a + (- a ) = 0

Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.

Видео:Координаты точки и координаты вектора 1.Скачать

Разность векторов

Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:

Формула вычитания векторов

Элементы вектора c равны попарной разности соответствующих элементов a и b .

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a — b = x — b_x; a_y — b_y> » data-order=» a — b = x — b_x; a_y — b_y> » style=»min-width:55.0847%; width:55.0847%;»> a — b = x — b_x; a_y — b_y>

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a — b = x — b_x; a_y — b_y; a_z — b_z> » data-order=» a — b = x — b_x; a_y — b_y; a_z — b_z> «> a — b = x — b_x; a_y — b_y; a_z — b_z>

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a — b = 1 — b₁; a₂ — b₂; . a_n — b_n> » data-order=» a — b = 1 — b₁; a₂ — b₂; . a_n — b_n> «> a — b = 1 — b₁; a₂ — b₂; . a_n — b_n>

Видео:Как построить точки в системе координат OXYZСкачать

Примеры задач

Задание 1
Вычислим сумму векторов и .

Задание 2
Найдем разность векторов и .

Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Сложение и вычитание векторов

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow ) .

Существование: Имеем два следующих случая:

Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow ) .

Из данного выше построения сразу же будет следовать единственность данного вектора.

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec + vec = left( + , + , + > right) )

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора ( overrightarrow ) выполняется равенство

Для произвольных точек ( A, B и C ) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Видео:Задача о векторах, построенных на медиане, биссектрисе и высоте треугольникаСкачать

Разность векторов. Вычитание векторов

Разность двух одинаковых векторов равна нулевому вектору :
( vec — vec = vec )

Длина нулевого вектора равна нулю:
( left| vec right| = 0 )

Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec — vec = left( — , — , — > right) )

Видео:Угол между векторами. 9 класс.Скачать

Умножение вектора на число

Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .

Длина вектора ( overrightarrow ) равна ( left|overrightarrow right|=left|kright||overrightarrow| ) ;

Обозначение: ( overrightarrow =koverrightarrow ) .

🔥 Видео

Уравнения стороны треугольника и медианыСкачать

Физика | Ликбез по векторамСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Математика это не ИсламСкачать