Как построить сечение пирамиды параллельное прямой основания (2 видео)

Методы построения сечений многогранников

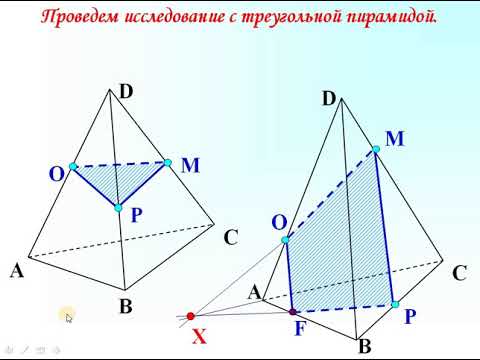
Разделы: Математика

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Данный материал характеризуется следующим особенностями:

Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.
В задачах используются в основном простейшие многогранники.
Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.

Чтобы решить задачу построения сечения многогранника ученик должен знать:

что значит построить сечение многогранника плоскостью;
как могут располагаться относительно друг друга многогранник и плоскость;
как задается плоскость;
когда задача на построение сечения многогранника плоскостью считается решенной.

Поскольку плоскость определяется:

тремя точками;
прямой и точкой;
двумя параллельными прямыми;
двумя пересекающимися прямыми,

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Существует три основных метода построения сечений многогранников:

Метод следов.
Метод вспомогательных сечений.
Комбинированный метод.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;
построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

В федеральный перечень учебников по геометрии для 10-11 класов входят учебники авторов:

Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др (Геометрия, 10-11);
Погорелова А.В. (Геометрия, 7-11);
Александрова А.Д., Вернера А.Л., Рыжик В.И. (Геометрия, 10-11);
Смирновой И.М. (Геометрия, 10-11);
Шарыгина И.Ф. (Геометрия, 10-11).

Рассмотрим подробнее учебники Л.С, Атанасяна и Погорелова А.В.

В учебнике Л.С. Атанасяна на тему “Построение сечений многогранников” выделено два часа. В 10 классе в теме “Параллельность прямых и плоскостей” после изучения тетраэдра и параллелепипеда отводится один час на изложение параграфа “Задачи на построение сечений”. Рассматриваются сечения тетраэдра и параллелепипеда. И тема “Параллельность прямых и плоскостей” завершается решением задач на одном или двух часах (всего задач на построение сечений в учебнике восемь).

В учебнике Погорелова А.В. на построение сечений отводится около трех часов в главе “Многогранники”: один – на изучение темы “Изображение призмы и построение ее сечений”, второй – на изучение темы “Построение пирамиды и ее плоских сечений” и третий – на решение задач. В списке задач, приведенных после темы, задач на сечение насчитывается всего около десяти.

Мы предлагаем систему уроков по теме “Построение сечений многогранников” для учебника Погорелова А.В.

Материал предлагается расположить в той последовательности, в какой он может применяться для обучения учащихся. Из изложения темы “Многогранники” предлагается исключить следующие параграфы: “Построение сечений призмы” и “Построение сечений пирамиды” с тем, чтобы систематизировать данный материал в конце этой темы “Многогранники”. Классифицировать его по тематике задач с примерным соблюдением принципа “от простого к сложному” можно весьма условно следующим образом:

Определение сечения многогранников.
Построение сечений призмы, параллелепипеда, пирамиды методом следов. (Как правило в школьном курсе стереометрии используются задачи на построение сечений многогранников, решаемые основными методами. Остальные методы, в связи с их более высоким уровнем сложности, учитель может оставить для рассмотрения на факультативных занятиях или на самостоятельное изучение. В задачах на построение основными методами требуется построить плоскость сечения, проходящую через три точки).
Нахождение площади сечений в многогранниках (без использования теоремы о площади ортогональной проекции многоугольника).
Нахождение площади сечений в многогранниках (с применением теоремы о площади ортогональной проекции многоугольника).

Содержание

СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.
(система уроков и факультативных занятий по теме “Построение сечений многогранников”)
Узнать ещё
Как построить сечение пирамиды
Пирамида и усеченная пирамида
Сечение, параллельное основанию пирамиды
🌟 Видео

СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.

(система уроков и факультативных занятий по теме “Построение сечений многогранников”)

Тема урока: “Построение сечений многогранников”.

Цель урока: ознакомление с методами построений сечений многогранников.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Как строить сечения тетраэдра и пирамидыСкачать

Как построить сечение пирамиды

Разберем, как построить сечение пирамиды, на конкретных примерах. Поскольку в пирамиде нет параллельных плоскостей, построение линии пересечения (следа) секущей плоскости с плоскостью грани чаще всего предполагает проведение прямой через две точки, лежащие в плоскости этой грани.

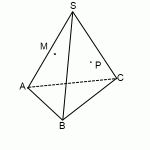
В простейших задачах требуется построить сечение пирамиды плоскостью, проходящей через данные точки, уже лежащие в одной грани.

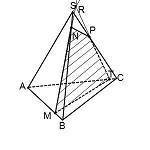
Построить сечение плоскостью (MNP)

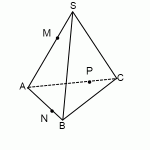
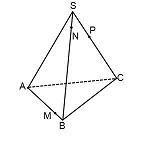
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Треугольник MNP — сечение пирамиды

Точки M и N лежат в одной плоскости ABS, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, значит, соединяем M и N сплошной линией.

Точки M и P лежат в одной плоскости ACS, поэтому через них проведем прямую. След — отрезок MP. Мы его не видим, поэтому отрезок MP проводим штрихом. Аналогично строим след PN.

Треугольник MNP — искомое сечение.

Если точка, через которую требуется провести сечение, лежит не на ребре, а на грани, то она не будет концом следа-отрезка.

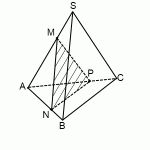
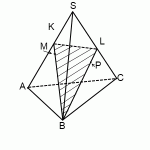
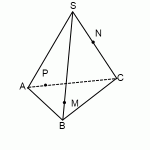
Пример. Построить сечение пирамиды плоскостью, проходящей через точки B, M и N, где точки M и N принадлежат, соответственно, граням ABS и BCS.

Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.

Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.

Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.

Треугольник BKL — искомое сечение.

Однако не всегда через данные в условии точки удается провести прямую. В этом случае нужно найти точку, лежащую на прямой пересечения плоскостей, содержащих грани.

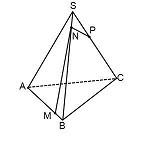
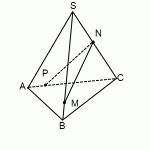
Пример. Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Точки M и N лежат в одной плоскость ABS, поэтому через них можно провести прямую. Получаем след MN. Аналогично — NP. Оба следа видимые, поэтому соединяем их сплошной линией.

Точки M и P лежат в разных плоскостях. Поэтому соединить их прямой не можем.

Продолжим прямую NP.

Она лежит в плоскости грани BCS. NP пересекается только с прямыми, лежащими в этой же плоскости. Таких прямых у нас три: BS, CS и BC. С прямыми BS и CS уже есть точки пересечения — это как раз N и P. Значит, ищем пересечение NP с прямой BC.

Точку пересечения (назовем ее H), получаем, продолжая прямые NP и BC до пересечения.

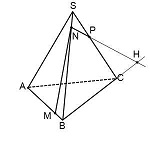
Эта точка H принадлежит как плоскости (BCS), поскольку лежит на прямой NP, так и плоскости (ABC), поскольку лежит на прямой BC.

Таким образом мы получили еще одну точку секущей плоскости, лежащей в плоскости (ABC).

Через H и точку M, лежащую в этой же плоскости, можем провести прямую.

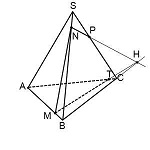
Получим след MT.

T — точка пересечения прямых MH и AC.

Так как T принадлежит прямой AC, то через нее и точку P можем провести прямую, так как они обе лежат в одной плоскости (ACS).

4-угольник MNPT — искомое сечение пирамиды плоскостью, проходящей через данные точки M,N,P.

Мы работали с прямой NP, продлевая ее для отыскания точки пересечения секущей плоскости с плоскостью (ABC). Если работать с прямой MN, приходим к тому же результату.

Рассуждаем так: прямая MN лежит в плоскости (ABS), поэтому пересекаться может только с прямыми, лежащими в этой же плоскости. У нас таких прямых три: AB, BS и AS. Но с прямыми AB и BS уже есть точки пересечения: M и N.

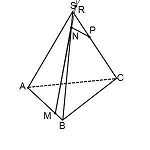
Значит, продлевая MN, ищем точку пересечения ее с прямой AS. Назовем эту точку R.

Точка R лежит на прямой AS, значит, она лежит и в плоскости (ACS), 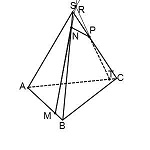которой принадлежит прямая AS.

Поскольку точка P лежит в плоскости (ACS), через R и P можем провести прямую. Получаем след PT.

Точка T лежит в плоскости (ABC), поэтому через нее и точку M можем провести прямую.

Таким образом, получили все то же сечение MNPT.

Рассмотрим еще один пример такого рода.

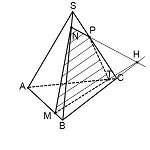
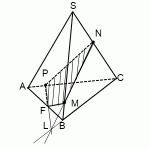
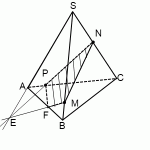
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.

Через точки M и N, лежащие в одной плоскости (BCS), проводим прямую. Получаем след MN (видимый).

Через точки N и P, лежащие в одной плоскости (ACS), проводим прямую. Получаем след PN (невидимый).

Через точки M и P прямую провести не можем.

1) Прямая MN лежит в плоскости (BCS), где есть еще три прямые: BC, SC и SB. С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.

Точка L принадлежит прямой BC, а значит, она лежит в плоскости (ABC). Поэтому через L и P, которая также лежит в плоскости (ABC) можем провести прямую. Ее след — PF.

F лежит на прямой AB, а значит, и в плоскости (ABS). Поэтому через F и точку M, которая также лежит в плоскости (ABS), проводим прямую. Ее след — FM. Четырехугольник MNPF — искомое сечение.

2) Другой путь — продолжить прямую PN. Она лежит в плоскости (ACS) и пересекается с прямыми AC и CS, лежащими в этой плоскости, в точках P и N.

Значит, ищем точку пересечения PN с третьей прямой этой плоскости — с AS. Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат водной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).

Видео:№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Пирамида и усеченная пирамида

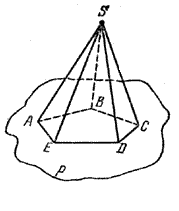
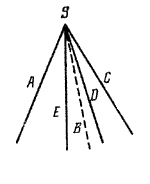
Как можно построить пирамиду? На плоскости р построим какой-либо многоугольник, например пятиугольник ABCDE. Вне плоскости р возьмем точку S. Соединив точку S отрезками со всеми точками многоугольника, получим пирамиду SABCDE (рис.).

Точка S называется вершиной, а многоугольник ABCDE — основанием этой пирамиды. Таким образом, пирамида с вершиной S и основанием ABCDE — это объединение всех отрезков [SM], где М ∈ ABCDE.

Треугольники SAB, SBC, SCD, SDE, SEA называются боковыми гранями пирамиды, общие стороны боковых граней SA, SB, SC, SD, SE — боковыми ребрами.

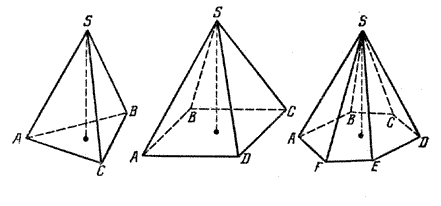
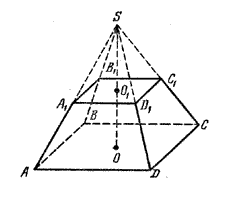
Пирамиды называются треугольными, четырехугольными, п-угольными в зависимости от числа сторон основания. На рис. даны изображения треугольной, четырехугольной и шестиугольной пирамид.

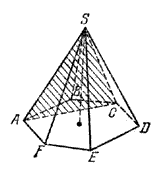
Плоскость, проходящая через вершину пирамиды и диагональ основания, называется диагональной, а полученное сечение — диагональным. На рис. 186 одно из диагональных сечений шестиугольной пирамиды заштриховано.

Отрезок перпендикуляра, проведенного через вершину пирамиды к плоскости ее основания, называется высотой пирамиды (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Пирамида называется правильной, если основание пирамиды—правильный многоугольник и вершина пирамиды проектируется в его центр.

Все боковые грани правильной пирамиды — конгруэнтные равнобедренные треугольники. У правильной пирамиды все боковые ребра конгруэнтны.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды. Все апофемы правильной пирамиды конгруэнтны.

Если обозначить сторону основания через а, а апофему через h, то площадь одной боковой грани пирамиды равна 1 /₂ ah .

Сумма площадей всех боковых граней пирамиды называется площадью боковой поверхности пирамиды и обозначается через S_бок.

Так как боковая поверхность правильной пирамиды состоит из n конгруэнтных граней, то

где Р — периметр основания пирамиды. Следовательно,

т. е. площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Площадь полной поверхности пирамиды вычисляется по формуле

Объем пирамиды равен одной трети произведения площади ее основания S_ocн. на высоту Н:

Вывод этой и некоторых других формул будет дан в одной из последующих глав.

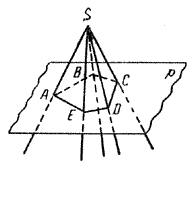
Построим теперь пирамиду другим способом. Пусть дан многогранный угол, например, пятигранный, с вершиной S (рис.).

Проведем плоскость р так, чтобы она пересекала все ребра данного многогранного угла в разных точках А, В, С, D, Е (рис.). Тогда пирамиду SABCDE можно рассматривать как пересечение многогранного угла и полупространства с границей р, в котором лежит вершина S.

Очевидно, что число всех граней пирамиды может быть произвольным, но не меньшим четырех. При пересечении трехгранного угла плоскостью получается треугольная пирамида, у которой четыре грани. Любую треугольную пирамиду иногда называют тетраэдром, что означает четырехгранник.

Усеченную пирамиду можно получить, если пирамиду пересечь плоскостью, параллельной плоскости основания.

На рис. дано изображение четырехугольной усеченной пирамиды.

Усеченные пирамиды также называются треугольными, четырехугольными, n-угольными в зависимости от числа сторон основания. Из построения усеченной пирамиды следует, что она имеет два основания: верхнее и нижнее. Основания усеченной пирамиды — два многоугольника, стороны которых попарно параллельны. Боковые грани усеченной пирамиды — трапеции.

Высотой усеченной пирамиды называется отрезок перпендикуляра, проведенного из любой точки верхнего основания к плоскости нижнего.

Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и плоскостью сечения, параллельной основанию. Высота боковой грани правильной усеченной пирамиды (трапеции) называется апофемой.

Можно доказать, что у правильной усеченной пирамиды боковые ребра конгруэнтны, все боковые грани конгруэнтны, все апофемы конгруэнтны.

Если в правильной усеченной n-угольной пирамиде через а и b_n обозначить длины сторон верхнего и нижнего оснований, а через h — длину апофемы, то площадь каждой боковой грани пирамиды равна

Сумма площадей всех боковых граней пирамиды называется площадью ее боковой поверхности и обозначается S_бок. . Очевидно, что для правильной усеченной n-угольной пирамиды

Так как па = Р и nb_n = Р₁ — периметры оснований усеченной пирамиды, то

т. е. площадь боковой поверхности правильной усеченной пирамиды равна половине произведения суммы периметров ее оснований на апофему.

Видео:Построение сечения пирамиды по трем точкамСкачать

Сечение, параллельное основанию пирамиды

1) боковые ребра и высота разделятся на пропорциональные части;

2) в сечении получится многоугольник, подобный основанию;

3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

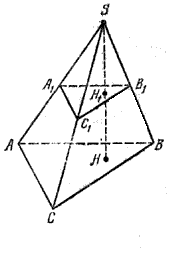
Теорему достаточно доказать для треугольной пирамиды.

Так как параллельные плоскости пересекаются третьей плоскостью по параллельным прямым, то (АВ) || (А₁В₁), (BС) ||( В₁C₁), (AС) || (A₁С₁) (рис.).

Параллельные прямые рассекают стороны угла на пропорциональные части, и поэтому

Соответственные углы треугольников ABC и A₁B₁C₁ конгруэнтны, как углы с параллельными и одинаково направленными сторонами. Поэтому

Площади подобных треугольников относятся, как квадраты соответствующих сторон:

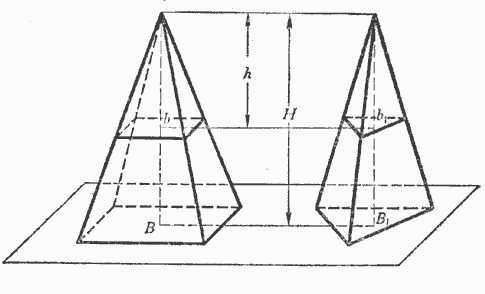
Теорема. Если две пирамиды с равными высотами рассечены на одинаковом расстоянии от вершины плоскостями, параллельными основаниям, то площади сечений пропорциональны площадям оснований.

Пусть (черт. 84) В и В₁— площади оснований двух пирамид, H — высота каждой из них, b и b₁ — площади сечений плоскостями, параллельными основаниям и удалёнными от вершин на одно и то же расстояние h.

Согласно предыдущей теореме мы будем иметь:

Следствие. Если В = В₁, то и b = b₁ , т. е. если у двух пирамид с равными высотами основания равновелики, то равновелики и сечения, равноотстоящие от вершины.