Как построить проекции равнобедренного треугольника

Страницы работы

Содержание работы

Санкт-Петербургский государственный морской технический университет

Кафедра компьютерной графики и информационного обеспечения

Домашнее задание №2

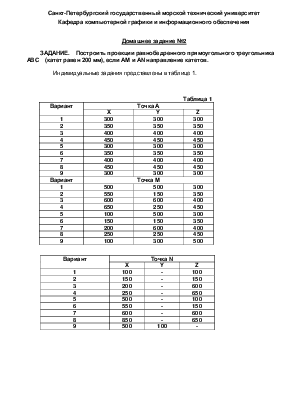
ЗАДАНИЕ. Построить проекции равнобедренного прямоугольного треугольника АВС (катет равен 200 мм), если АМ и АN направление катетов.

Индивидуальные задания представлены в таблице 1.

ПРИМЕР ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ №2. Построить проекции равнобедренного прямоугольного треугольника АВС с вершиной прямого угла В на прямой k и стороной АС на прямой L.

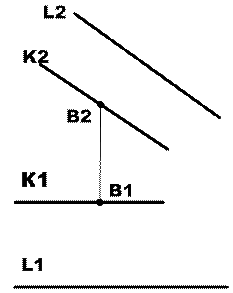
Начальное графическое условие

(обязательно его наличие)

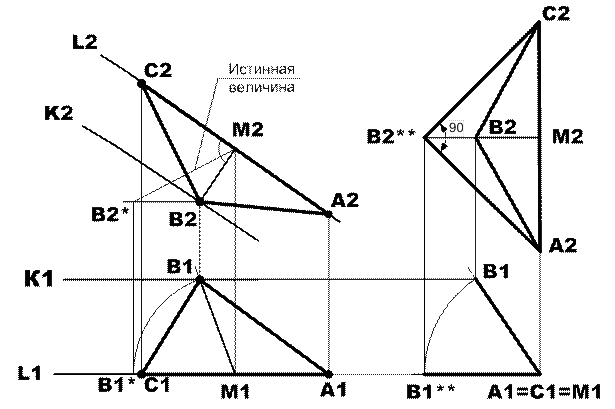
Комментарий к решению задачи: для решения конструктивных задач полезно рисовать модель заданной фигуры в плане, для того, чтобы грамотно использовать ее геометрические характеристики. Одновременно надо внимательно проанализировать начальное условие. На рис.1 представлена модель в плане, а на рис.2 решение поставленной задачи.

Рис.1. Модель задачи в плане.

Из начального условия видно, что заданные прямые kиL параллельны фронтальной плоскости проекций и, следовательно, могут быть сделаны следующие важные выводы (см. рис.2):

— из заданной точки В2 можно проводить линию, перпендикулярную к фронтальным проекциям прямых k2 и L2 одновременно;

-т.к. гипотенуза заданного треугольника должна располагаться на прямой L, то ее фронтальная проекция А2С2 будет равна истинной величине гипотенузы АС.

Сделанные выводы позволяют создать модель решения задачи (рис.1), в которой искомый треугольник построен следующим образом:

— из точки М проведена высота ВМ;

— известно, что высота, проведенная из вершины прямого угла, делит равнобедренный прямоугольный треугольник на два равных равнобедренных прямоугольных треугольника с вершиной прямого угла у основания высоты. Следовательно ВМ=МА, т.е. гипотенуза искомого треугольника в два раза больше его высоты;

— поскольку проекции высоты ВМ могут быть легко построены, то не составляет труда найти истинную величину гипотенузы АС и, следовательно, построить проекции треугольника АВС.

Рис.2. Построение проекций равнобедренного прямоугольного треугольника.

1) из точки В2 провести перпендикуляр к L2 и построить проекции высоты В2М2 и В1М1;

2) методом вращения, повернув высоту ВМ до положения параллельного фронтальной плоскости проекций, определить ее истинную величину-это проекция М2В2*;

3) отложить отрезок М2В2* на линии L2 в разные стороны от точки М2 для построения проекций вершин А2 и С2 искомого треугольника;

4) построить фронтальную А2В2С2 и горизонтальную А1В1С1 проекции искомого треугольника.

Проверка: построенные проекции треугольника искажены, поскольку заданный треугольник находится в общем положении в пространстве. Убедиться в правильности выполненных построений можно только определив истинную величину треугольника. Для этого методом вращения сначала треугольник переведен в проецирующее положение, которому соответствуют фронтальная проекция А2С2В2 при вертикальном расположении гипотенузы А2С2 и горизонтальная проекция в виде отрезка прямой А1С1В1. Далее проецирующий треугольник надо повернуть до положения параллельного плоскости П2, которому соответствуют горизонтальная проекция А1С1В1** и фронтальная проекция А2С2В2**. При этом проекция А2С2В2** равна по величине истинной. На рис.2 видно, что истинная величина является равнобедренным прямоугольным треугольником с вершиной прямого угла в точке В, что соответствует условию задачи.

Видео:ПРОЕКЦИИ РАВНОСТОРОННЕГО ТРЕУГОЛЛЬНИКА НА П1/П2 и углы наклона его плоскости к плоскостям проекцийСкачать

Московский государственный университет путей сообщения (МИИТ)

ЗАДАЧА№1

Построить проекции равнобедренного прямоугольного треугольника АВС, если известно, что катет ВС принадлежит прямой KL.

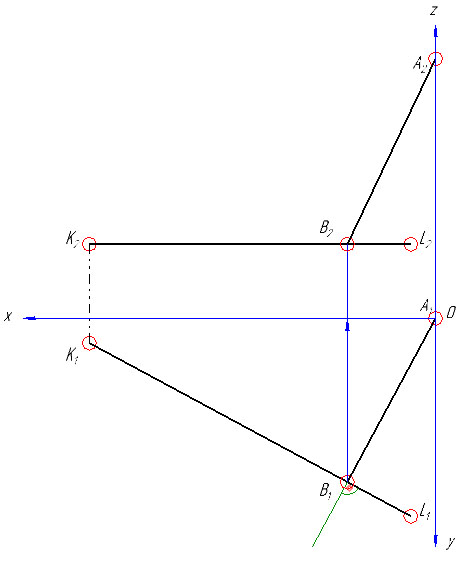
Исходными данными задачи является точка А – вершина треугольника и прямая KL, на которой расположен его катет ВС. Прямая KL – линия уровня (параллельна плоскости проекций П₁ или П₂).

РЕШЕНИЕ:

1) По заданным координатам в таблице с вариантами строим проекции точек А, Р и прямой KL, в нашей задаче KL параллельна П₁ – т.е. горизонталь (координаты по оси z равны 30).

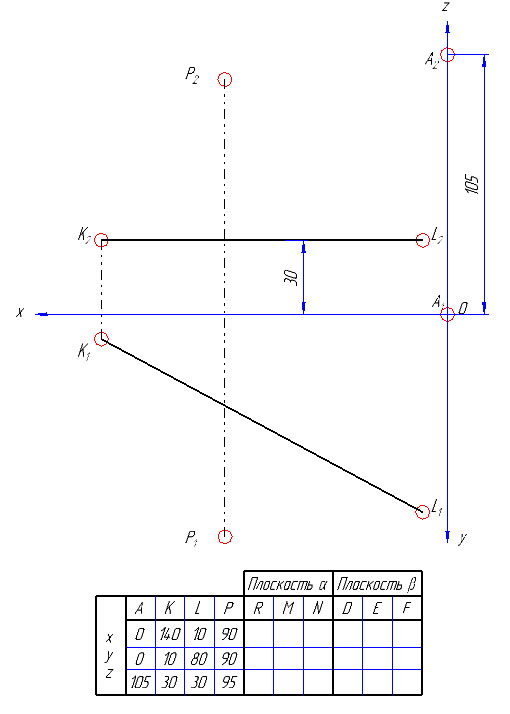
2) Из точки А опускаем перпендикуляр на прямую KL (так как искомый треугольник прямоугольный, а вершина А задана).

Отмечаем основание перпендикуляра – точку В (В₁). Фронтальную проекцию точки В (В₂) получаем по линии связи на К₂L₂.

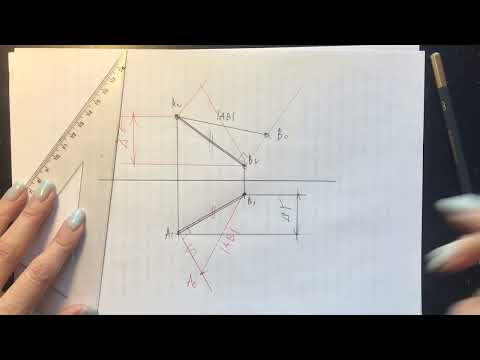
3) Определяем натуральную величину катета АВ треугольника АВС способом прямоугольного треугольника: для этого на фронтальной проекции берем отрезок равный разнице координат проекций точек А и В – дельта z, и под прямым углом к горизонтальной проекции отрезка AB (A₁B₁) откладываем отрезок равный дельта z, получаем точку А₀. В₁А₀ – будет натуральной величиной катета (отрезка) АВ.

4) На прямой KL от точки В в любую сторону откладываем натуральную величину катета АВ (так как в равнобедренном прямоугольном треугольнике оба катета равны). В нашем случае откладываем на горизонтальной проекции K₁L₁ – т.к. KL – горизонталь и проецируется в натуральную величину именно на плоскость П₁. Получаем точку С (сначала проекцию С₁ и по линии связи C₂).

Соединяем точку А с точкой С. Треугольник АВС – искомый.

ЗАДАЧА№3

Определить натуральную величину расстояния от точки Р до плоскости.

РЕШЕНИЕ:

Кратчайшим расстоянием от точки до плоскости является отрезок перпендикуляра.

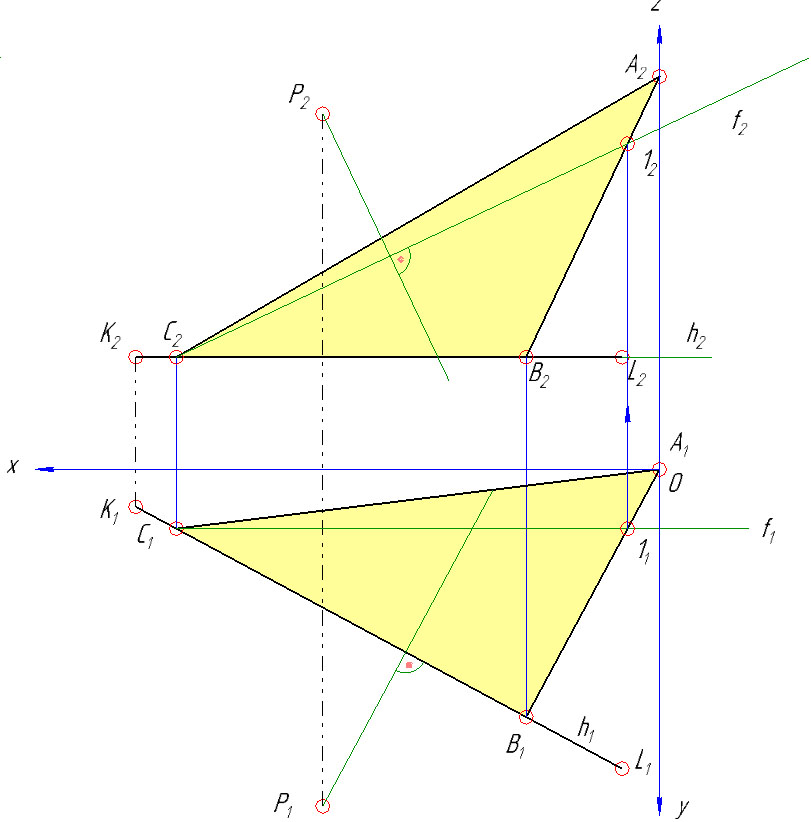
1) На основании теоремы о перпендикуляре к плоскости горизонтальная проекция перпендикуляра из точки Р проводится перпендикулярно к горизонтальной проекции горизонтали h. Независимо от горизонтальной проекции строится его фронтальная проекция. Для этого по плоскости найденного треугольника АВС проведена фронталь ƒ. Фронтальная проекция перпендикуляра должна быть перпендикулярна фронтальной проекции фронтали ƒ.

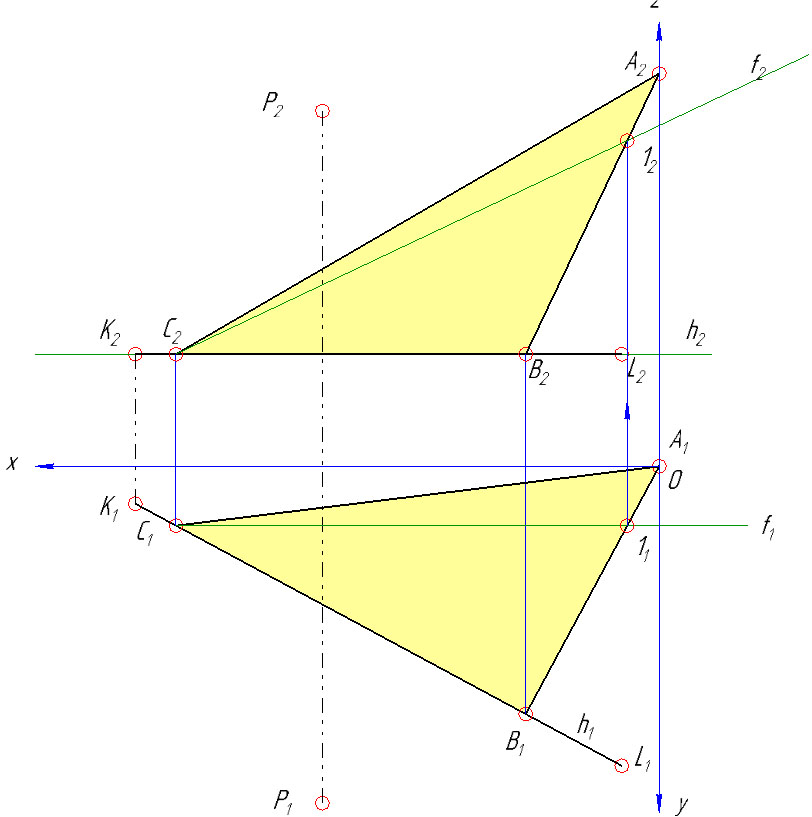
2) Прямая перпендикуляра из точки Р заключена в горизонтальнопроецирующую плоскость γ₁. Затем определена линия пересечения 2-3 вспомогательной плоскости γ с заданной плоскостью треугольника АВС.

В пересечении линии 2-3 с прямой n найдена искомая точка Q. Сначала определяется фронтальная проекция Q₂, а затем по линии проекционной связи определена ее горизонтальная Q₁ проекция.

3) Натуральная величина перпендикуляра PQ определена способом прямоугольного треугольника, аналогично как в задаче №1 определяли натуральную величину катета АВ.

Эпюра с задачами 1 и 3 — вариант 24

ЗАДАЧА №2.

Построить линию пересечения двух плоскостей заданных треугольниками α(DEF) и β(RMN), координаты вершин которых заданы в таблице исходных данных.

РЕШЕНИЕ:

1) По заданным координатам строим проекции всех точек, получаем проекции треугольников DEF и RMN.

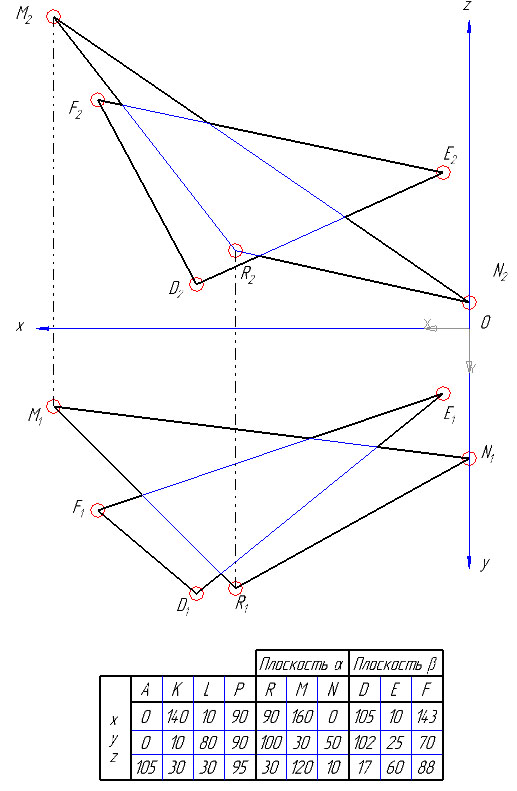
2) Решение задачи можно упростить, если вспомогательные проецирующие плоскости провести через прямые, задающие плоскость.

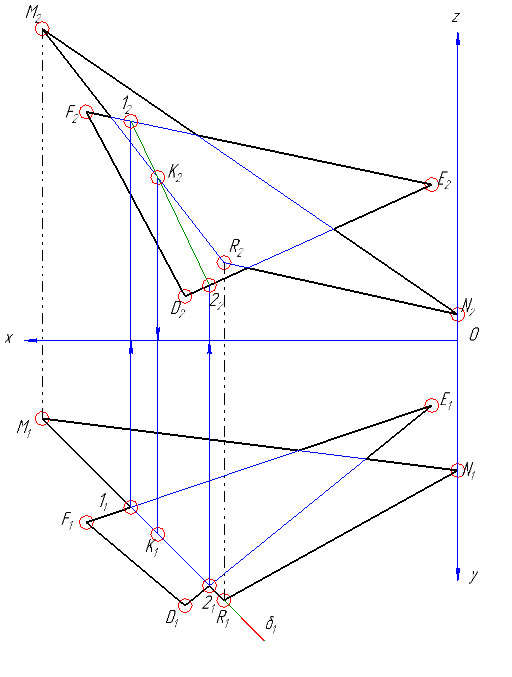
Так точка K этой линии определена с помощью горизонтальнопроецирущей плоскости δ₁, проведенной через сторону RM треугольника MNR. Именно линия RM является линией пересечения плоскости треугольника β(RMN) с вспомогательной плоскостью δ. Та же плоскость пересекает треугольник α(DEF) по линии 1-2.

Точка K, общая для трех плоскостей (двух заданных α и β и вспомогательной δ), находится в пересечении прямых 1-2 и RM.

Следует отметить, что если вспомогательная плоскость δ горизонтальнопроецирущая, то сначала определяется фронтальная проекция точки K₂, т.е. K₂ = 1₂-2₂∩R₂M₂, а затем по линии проекционной связи находится K₁ – горизонтальная проекция точки K.

3) Аналогично, заключая сторону DE во фронтальнопроецирующую плоскость γ₂, находится точка L. Прямая KL – линия пересечения заданных плоскостей.

4) Для определения видимости этих треугольников достаточно установить относительное расположение одной из сторон одного треугольника относительно стороны другого треугольника. Таким образом, вопрос видимости плоскостей сводится к определению видимости двух скрещивающихся прямых.

Определим видимость стороны DE треугольника DEF относительно стороны MN треугольника RMN на фронтальной плоскости проекции. Для этого проведем луч зрения s перпендикулярно П₂ через точку пересечения фронтальных проекций D₂E₂ и M₂N₂. В пересечении D₂E₂ и M₂N₂ расположены две конкурирующие по видимости точки (5₂ и 4₂). Точка 4 принадлежит стороне MN, а точка 5 – стороне DE. По горизонтальной проекции устанавливаем, что луч зрения сначала встретит D₁E₁ в точке 5₁, а затем M₁N₁ в точке 4₁. Следовательно, фронтальная проекция D₂E₂ – видима.

Аналогично определяется видимость треугольников и на горизонтальной проекции. Луч зрения при этом следует провести перпендикулярно к П₁ через две конкурирующие на П₁ точки скрещивающихся прямых (например, луч s / , проходящий через точки 1 и 6, соответственно принадлежащие прямым MR и ЕF).

Эпюр с задачей №2

ЗАКАЗЫВАЙТЕ ЧЕРТЕЖИ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ МГУПС

тел. (whatsup) 8-950-790-65-90

Видео:ПОСТРОИТЬ ПРОЕКЦИИ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА ПО ЗАДАННЫМ УСЛОВИЯМ. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.Скачать

Начертательная геометрия

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Институт пути, строительства и сооружений

Кафедра «Начертательная геометрия и черчение»

Рекомендовано редакционно-издательским советом университета в качестве методических указаний для студентов ИПСС

. Начертательная геометрия. — М.: МИИТ, 2008.- 21с.

Настоящие методические указания составлены с целью оказания помощи студентам в процессе выполнения домашней работы №1 по начертательной геометрии по теме «Точка, прямая, плоскость».

©Московский государственный университет путей сообщения (МИИТ), 2008

Настоящие методические указания составлены с целью оказания помощи студентам в процессе выполнения домашней работы по начертательной геометрии № 1.

Работа №1 – «Взаимное расположение точки, прямой и плоскости», содержит метрические, позиционные и некоторые конструктивные задачи, связанные с построением проекций геометрических фигур, отвечающих определенным условиям.

В этой работе студент выполняет три задачи:

1) построение плоской фигуры по заданным условиям;

2) построение проекций линии пересечения двух плоскостей и определение относительной видимости;

3) определение натуральной величины расстояния от точки до плоскости.

Для выполнения указанных задач необходимо знание следующих разделов курса: сущность метода ортогонального проецирования и понятия о координатах точки; основные свойства параллельного проецирования; различные положения прямой относительно плоскостей проекций; определение длины отрезка прямой;

теорема о проецировании прямого угла; плоскость и ее главные линии; пересекающиеся плоскости; теорема о перпендикуляре к плоскости.

Работа выполняется в карандаше на чертежной бумаге формата А3 (297×420). Пример оформления работы приведен на рис.12. В левой половине листа выполняются задачи №1 и 3, на правой половине – задача №2. В правом нижнем углу формата размещается основная надпись (размер 134×40) и таблица исходных данных.

Построить проекции равнобедренного прямоугольного треугольника АВС, если известно, что катет ВС принадлежит прямой KL.

Исходными данными задачи является точка А – вершина треугольника и прямая KL, на которой расположен его катет ВС (см рис.1). Прямая KL – линия уровня (параллельна плоскости проекций П1или П2).

Построение точки А на эпюре выполняется по заданным координатам.

Известно, что каждая проекция точки определяется двумя координатами: горизонтальная проекция координатами X и Y – А1(X, Y), фронтальная – А2(X, Z). Поэтому на оси абсцисс (OX) от начала координат O откладывается отрезок, равный XА. Затем, через полученную точку перпендикулярно к оси OX проводится линия проекционной связи, на которой откладываются отрезки, равные YA и ZA (с учетом знака координат). Построение проекций прямой KL выполняется по двум ее точкам K и L, координаты которых заданы.

Так как эти точки прямой находятся на одном расстоянии от плоскости проекций П1 или П2, то справедливы равенства ZK=ZL или YK=YL. Из этого следует, что заданная прямая KL – прямая уровня, т. е. либо она горизонтальная (при ZK=ZL), либо фронтальная (при YK=YL).

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ

1. Из точки А опускают перпендикуляр на прямую KL (так как искомый треугольник прямоугольный, а вершина А задана) рис.2.

2. Отмечают основание перпендикуляра – точку В.

3. Определяют натуральную величину катета АВ треугольника АВС.

4.На прямой KL от точки В в любую сторону откладывают натуральную величину катета АВ (так как в равнобедренном прямоугольном треугольнике оба катета равны). Получают точку С. Задача может иметь два решения, так как на прямой KL можно найти вершину С′, симметричную С относительно точки В.

5. Соединяют точку А с точкой С. Треугольник АВС – искомый.

Решение задачи №1 на эпюре приведено на рис.3. С левой стороны исходные данные задачи.

1. Из точки А опускают перпендикуляр на прямую KL. Так как заданная прямая параллельна плоскости П2, прямой угол между перпендикуляром и прямой KL проецируется в натуральную величину на ту же плоскость. (На основании теоремы о проецировании прямого угла). При решении задачи вначале строят фронтальную проекцию перпендикуляра.

2. Отмечают фронтальную проекцию В2 точки пересечения перпендикуляра с прямой KL. А2В2 – фронтальная проекция перпендикуляра.

3. В проекционной связи на K1L1определяют горизонтальную проекцию В1 – основания перпендикуляра.

4. Соединив А1 с В1 получают горизонтальную проекцию перпендикуляра А1В1. Отрезки А1В1 и А2В2 – проекции катета АВ треугольника АВС.

5. Для построения второго катета ВС (ВС=АВ) необходимо знать действительную величину отрезка АВ (катет АВ представляет собой прямую общего положения, которая не проецируется в натуральную величину ни на одну из плоскостей проекций). Для определения ее натуральной величины использован способ прямоугольного треугольника. Так, на эпюре натуральная величина АВ определена как

гипотенуза прямоугольного треугольника А1В1А0, катетами которого являются отрезки А1В1 и ΔZ как — разность координат ZA и ZB.

6. Так как второй катет по условию задачи расположен на фронтали, то от точки В2 на фронтальной проекции K2L2 прямой KL в любую сторону откладывают величину отрезка В1А0 и отмечают точку С2.

7. В проекционной связи на K1L1 находят точку С1.

8. Соединив С2 с А2 и С1 с А1 получают проекции искомого треугольника.

Построить линию пересечения двух плоскостей и определить их относительную видимость.

Линией пересечения двух плоскостей является прямая линия, для построения которой необходимо знать: либо две точки, общие для этих плоскостей, либо одну точку и направление линии пересечения.

Сначала рассмотрим частные случаи пересечения плоскостей.

1. Одна из заданных плоскостей – плоскость проецирующая.

На рис.4 построена линия пересечения плоскости общего положения, заданной двумя пересекающимися прямыми α(a ∩ b), с фронтальнопроецирующей плоскостью β2(β ┴ П2).

Линия пересечения данных плоскостей определяется двумя точками 1 и 2, в которых прямые a и b плоскости α пересекают проецирующую плоскость β.

Сначала строится фронтальная проекция линии пересечения 12 – 22, а затем в проекционной связи ее горизонтальная проекция 11 – 21. Следует заметить, что фронтальная проекция линии

пересечения заданных плоскостей 12 – 22 совпадает с фронтальным следом проецирующей плоскости β.

2. Одна из заданных плоскостей — плоскость уровня.

В этом случае для построения линии пересечения плоскостей достаточно знать лишь одну точку, общую обеим плоскостям, и направление линии пересечения.

Так на рис.5 плоскость общего положения α(h∩n) пересекается с горизонтальной плоскостью β по горизонтальной линии, направление которой известно. Поэтому горизонтальная проекция линии пересечения пройдет через общую обеим плоскостям точку 11 и параллельно горизонтальной проекции горизонтали h1.

Общий прием построения линии пересечения двух плоскостей приведен на рис.6.

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ

1. Плоскости α и β пересекают вспомогательной плоскостью γ.

2. Строят линии пересечения вспомогательной плоскости с заданными α и β. Это линии 1-2 и 3-4.

3. Отмечают точку пересечения построенных линий 1-2 ∩ 3-4 = М.

Для построения второй точки N алгоритм решения повторяют.

Пример. Построить проекции линии пересечения двух плоскостей общего положения.

Рис.7

Как видно из рис.7 одна из плоскостей α задана треугольником α(АВС), а вторая β – параллельными прямыми (m ║ n). Для решения задачи обе плоскости пересечены вспомогательными проецирующими плоскостями γ2 и δ2.

(В качестве вспомогательных плоскостей можно было провести плоскости уровня). Плоскость γ пересекает плоскость α(АВС) по линии 1-2, а плоскость β(m ║ n) — по линии 3-4. В пересечении этих линий определена точка K, общая для двух плоскостей.

Аналогично пересекая заданные плоскости второй вспомогательной плоскостью δ, можно найти вторую точку L общую обеим плоскостям.

Следует заметить, что если вспомогательные плоскости γ и δ параллельны, то и линия пересечения 1-2 параллельна 5-6, а линия 3-4 параллельна линии 7-8.

Прямая, проходящая через точки K и L, определяет искомую линию пересечения плоскостей α и β.

В работе №1 студенты строят линию пересечения двух плоскостей заданных треугольниками α(DEF) и β(RMN), координаты

вершин которых заданы в таблице исходных данных.

Решение задачи можно упростить (рис.8) если вспомогательные проецирующие плоскости провести через прямые, задающие плоскость.

Так точка K этой линии определена с помощью фронтальнопроецирущей плоскости γ2, проведенной через сторону RN треугольника MNR. Именно линия RN является линией пересечения плоскости треугольника β(RMN) с вспомогательной плоскостью γ. Та же плоскость пересекает треугольник α(DEF) по линии 1-2.

Точка K, общая для трех плоскостей (двух заданных α и β и вспомогательной γ), находится в пересечении прямых 1-2 и RN.

Следует отметить, что если вспомогательная плоскость γ фронтальнопроецирущая, то сначала определяется горизонтальная проекция точки K1, т. е. K1 = 11-21∩R1N1, а затем по линии проекционной связи находится K2 – фронтальная проекция точки K.

Аналогично, заключая сторону DF в горизонтальнопроецирующую плоскость δ1, находится точка L. Прямая KL – линия пересечения заданных плоскостей.

Для определения видимости этих треугольников достаточно установить относительное расположение одной из сторон одного треугольника относительно стороны другого треугольника. Таким образом, вопрос видимости плоскостей сводится к определению видимости двух скрещивающихся прямых.

Например, определим видимость стороны DE треугольника DEF относительно стороны MN треугольника RMN на фронтальной плоскости проекции (см рис.8). Для этого проведем луч зрения s перпендикулярно П2 через точку пересечения фронтальных проекций D2E2 и M2N2. В пересечении D2E2 и M2N2 расположены две конкурирующие по видимости точки (52 и 62). Точка 5 принадлежит стороне MN, а точка 6 – стороне DE. По горизонтальной проекции устанавливаем, что луч зрения сначала встретит D1E1 в точке 61, а затем M1N1 в точке 51. Следовательно, фронтальная проекция D2E2 – видима.

Аналогично определяется видимость треугольников и на горизонтальной проекции. Луч зрения при этом следует провести перпендикулярно к П1 через две конкурирующие на П1 точки скрещивающихся прямых (например, луч s/, проходящий через точки 3 и 7, соответственно принадлежащие прямым MR и DF).

Определить натуральную величину расстояния от точки Р до плоскости.

Кратчайшим расстоянием от точки до плоскости является отрезок перпендикуляра.

Для решения задачи необходимо:

1. Из заданной точки Р опустить перпендикуляр на плоскость α.

2. Определить точку пересечения (точка К) перпендикуляра с плоскостью.

3. Определить натуральную величину перпендикуляра.

Рассмотрим более подробно каждый пункт приведенного выше алгоритма.

Пример 1. Из точки Р опустить перпендикуляр n на плоскость α(a∩b)

Рис.9

На основании теоремы о перпендикуляре к плоскости горизонтальная проекция n1 перпендикуляра n проводится перпендикулярно к горизонтальной проекции горизонтали h. Не — зависимо от горизонтальной проекции строится его фронтальная проекция. Для этого по плоскости α(a∩b) проведена произвольная фронталь ƒ. Фронтальная проекция перпендикуляра должна быть перпендикулярна фронтальной проекции фронтали ƒ.

Пример 2. Построить точку пересечения прямой n с плоскостью α. Пространственное решение задачи на рис.10.

Задача решается в три этапа:

1. Данная прямая n заключается во вспомогательную плоскость β

Построения будут простейшими, если β будет проецирующей;

2. Строится линия пересечения MN вспомогательной плоскости β с заданной α

3. В пересечении полученной линии MN с заданной n находится искомая точка K

Пример 3. Определить точку К пересечения перпендикуляра n с плоскостью α(h∩ƒ) и натуральную величину перпендикуляра (рис.11).

Прямая n заключена во фронтальнопроецирующую плоскость β, n € β. Затем определена линия пересечения 1-2 вспомогательной плоскости β с заданной плоскостью α(h∩ƒ), 1-2=β∩α.

В пересечении линии 1-2 с прямой n найдена искомая точка К. Сначала определяется горизонтальная проекция К1(К1=11-21∩n1), а затем по линии проекционной связи определена ее фронтальная К2 проекция.

Натуральная величина перпендикуляра определена способом прямоугольного треугольника.

Исходными данными для решения задачи 3 являются точка Р, заданная координатами и плоскость треугольника АВС, проекции которого построены в задаче № 1.

1. , Начертательная геометрия – М.: Высшая школа, 2005г.

2. , Начертательная геометрия – М.: Высшая школа, 1963г.

3. , Начертательная геометрия – М.: Высшая школа, 1982г.

Методические указания к

Подписано в печать — Формат 60х84/16 Тираж 300

Усл.- печ. л. 1,5 Изд. № Заказ №

Москва, ул. Образцова, 15. Типография МИИТа

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Институт пути, строительства и сооружений

Кафедра «Начертательная геометрия и черчение»

🔥 Видео

Построение равнобедренного треугольникаСкачать

Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Построение треугольника в трёх проекцияхСкачать

Начертательная геометрия. Задача 1Скачать

Строим проекции равнобедренной трапеции и определяем углы наклона ее высоты и плоскости к П1 и П2Скачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Как построить равнобедренный или равносторонний треугольник по клеткам.Скачать

Строим проекции параллелограмма и определяем углы наклона плоскости фигуры к плоскостям проекций.Скачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Построение проекции пирамиды. Метод прямого треугольника.Скачать

Построить проекции линии и точек на ней по заданным координатам. Начертательная геометрияСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Построение призмы высотой 30ммСкачать

Геометрия - Построение правильного треугольникаСкачать

Найти натуральную величину отрезка с помощью прямоугольного треугольника. #отрезка #геометрияСкачать

Треугольная пирамида. Проекции точек на гранях. Сечение. Урок23.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

[Решение задач по начертательной геометрии] Построение проекции пирамидыСкачать

Нахождение натуральной величины отрезка методом прямоугольного треугольникаСкачать