Как построить правильный квадрат вписанный в окружность с помощью циркуля (4 видео)

Квадрат вписанный в окружность

Содержание

Определение
Формулы
Радиус вписанной окружности в квадрат
Радиус описанной окружности около квадрата
Сторона квадрата
Площадь квадрата
Периметр квадрата
Диагональ квадрата
Как построить квадрат в окружности с помощью циркуля?
Как построить циркулем?
Как вычислить квадрат в окружности?
Как найти диагональ в квадрате?
Техническое черчение
Popular
Основы черчения
Строительное
Машиностроительное
🎬 Видео

Видео:Как построить квадрат, два способаСкачать

Определение

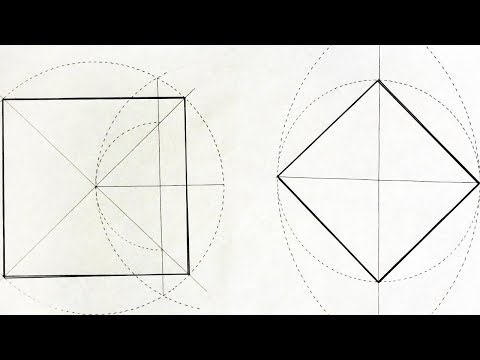
Квадрат, вписанный в окружность — это квадрат, который находится
внутри окружности и соприкасается с ней углами.

На рисунке 1 изображена окружность, описанная около
квадрата и окружность, вписанная в квадрат.

Видео:Построение правильного квадрата.Скачать

Формулы

Радиус вписанной окружности в квадрат

Радиус вписанной окружности в квадрат, если известна сторона:

Радиус вписанной окружности в квадрат, если известен периметр:

Радиус вписанной окружности в квадрат, если известна площадь:

Радиус вписанной окружности в квадрат, если известен радиус описанной окружности:

Радиус вписанной окружности в квадрат, если известна диагональ:

Радиус описанной окружности около квадрата

Радиус описанной окружности около квадрата, если известна сторона:

Радиус описанной окружности около квадрата, если известен периметр:

Радиус описанной окружности около квадрата, если известнаплощадь:

Радиус описанной окружности около квадрата, если известен радиус вписанной окружности:

Радиус описанной окружности около квадрата, если известнадиагональ:

Сторона квадрата

Сторона квадрата вписанного в окружность, если известнаплощадь:

Сторона квадрата вписанного в окружность, если известнадиагональ:

Сторона квадрата вписанного в окружность, если известен периметр:

Площадь квадрата

Площадь квадрата вписанного в окружность, если известна сторона:

Площадь квадрата вписанного в окружность, если известен радиус вписанной окружности:

Площадь квадрата вписанного в окружность, если известен радиус описанной окружности:

Площадь квадрата вписанного в окружность, если известен периметр:

Площадь квадрата вписанного в окружность, если известна диагональ:

Периметр квадрата

Периметр квадрата вписанного в окружность, если известна сторона:

Периметр квадрата вписанного в окружность, если известна площадь:

Периметр квадрата вписанного в окружность, если известенрадиус вписанной окружности:

Периметр квадрата вписанного в окружность, если известен радиус описанной окружности:

Периметр квадрата вписанного в окружность, если известна диагональ:

Диагональ квадрата

Диагональ квадрата вписанного в окружность, если известна сторона:

Диагональ квадрата вписанного в окружность, если известна площадь:

Диагональ квадрата вписанного в окружность, если известен периметр:

Диагональ квадрата вписанного в окружность, если известен радиус вписанной окружности:

Диагональ квадрата вписанного в окружность, если известен радиус описанной окружности:

Видео:Как вписать квадрат в окружностьСкачать

Как построить квадрат в окружности с помощью циркуля?

Видео:Построение 8 угольника циркулемСкачать

Как построить циркулем?

Примеры

Циркулем проводим окружности с центром в точках A и B радиусом AB.
Находим точки пересечения P и Q двух построенных окружностей (дуг).
По линейке проводим отрезок или линию, проходящую через точки P и Q.
Находим искомую середину отрезка AB — точку пересечения AB и PQ.

Видео:Построение пятиугольника циркулем и линейкойСкачать

Как вычислить квадрат в окружности?

S = 4 × r 2 , где r — это радиус вписанной окружности.

Видео:Построение пятиугольника циркулемСкачать

Как найти диагональ в квадрате?

d=√(2a 2 )

Данная формула применима ко всем случаям, когда необходимо найти диагональ квадрата. При этом в задаче может быть дан не сам квадрат, а форма квадрата как осевое сечение цилиндра, например, тогда длина диагонали квадрата равна диагонали сечения.

Видео:Построение квадрата циркулем по заданной сторонеСкачать

Техническое черчение

Основы черчения

Строительное

Машиностроительное

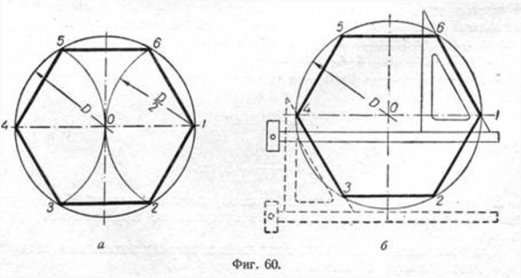
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.

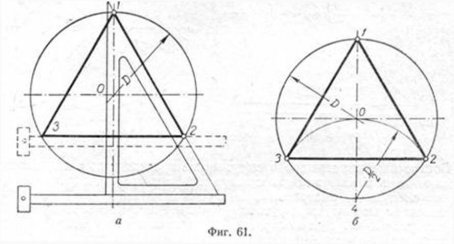
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.

Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

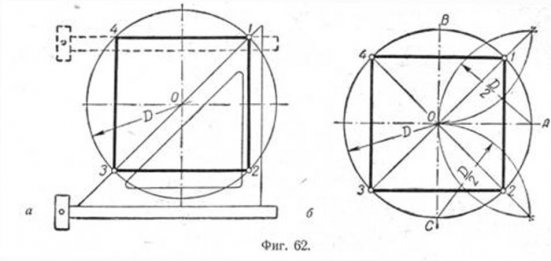
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

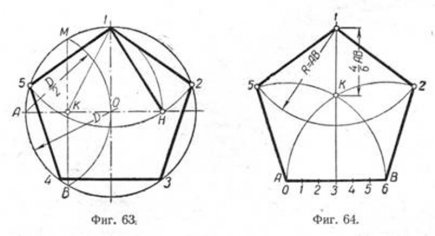
Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.

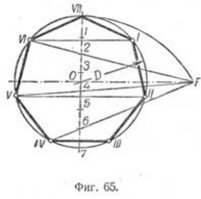
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

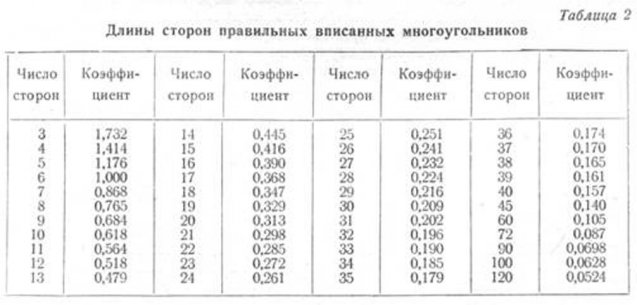
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.