Как построить овал в черчении через окружность (5 видео)

Чертежик

Содержание

Метки
Построение овала
Приемы построения эллипса
План-конспект урока по черчению на тему «Понятие о лекальных и циркулярных кривых, построение овала и эллипса»
«Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
🎥 Видео

Метки

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Построение овала

Рассмотрим построение овала двумя методами: окружности и параллелограмма.

Воспользуемся методом окружности.

1.) Начинаем чертить с построения осей.

2.) Чертим окружность

3.) Чертим дуги ЕА и BD радиусом ЕС

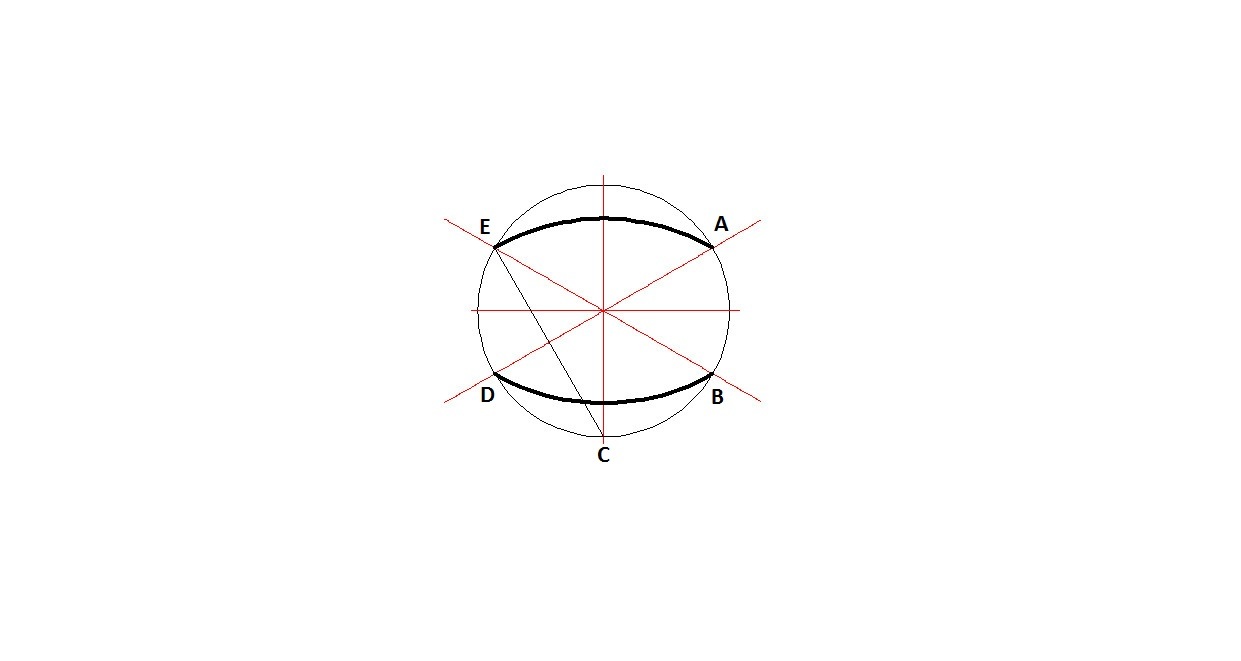
4.) Чертим дуги ED и AB радиусом FB

Применим метод параллелограмма.

1.) Начинаем с построения осевых линий

2.) Чертим линии параллельные осевым линиям. Где d — диаметр окружности.

3.) Строим дуги HB и DF радиусом HE4.) Продолжаем с черчения дуги BD радиуса MB и дуги FH радиусом PH

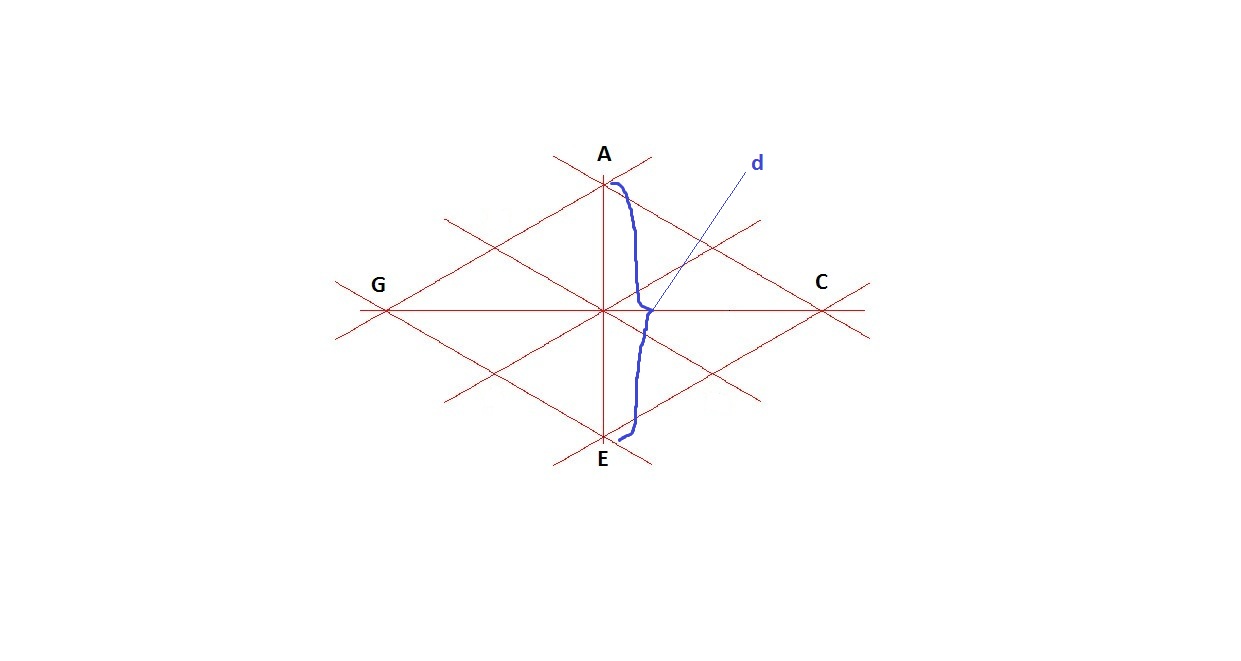
Применение построения овала на чертежах вы можете посмотреть здесь

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Приемы построения эллипса

Эллипс может быть построен как лекальная и как циркульная кривая.

Лекальная кривая строится по точкам, которые затем плавно соединяются от руки или при помощи лекала (способ 1).

Циркульная кривая строится при помощи циркуля как кривая, состоящая из четырёх сопрягающихся дуг окружностей (способы 2, 3).

Рассмотрим построение эллипса в аксонометрической плоскости х’О’у’. Аналогичными будут построения в других плоскостях. Только необходимо учитывать ориентацию осей эллипса. Возьмём окружность произвольного радиуса и построим её прямоугольную изометрию и диметрию разными способами, заготовив предварительно треугольники пропорциональности (рис. 84).

Способ L Лекальная кривая. Строим аксонометрию по восьми точкам, которыми будут являться концы осей и сопряжённых диаметров.

В прямоугольной изометрии (рис. 85, а) приведённые коэффициенты искажения по всем осям равны 1. Поэтому на осях х’ и у’ от центра О‘ откладываем радиус 7? окружности, на оси г’ — малую полуось эллипса 0,717?, на прямой, перпендикулярной z’, — большую его полуось 1,22R.

Для определения размеров большой и малой полуосей эллипса откладываем на натуральной шкале (1:1) треугольника пропорциональности для изометрии радиус окружности R, и из точки А проецируем его на остальные шкалы. На верхней шкале получаем размер 1,227?, на нижней — 0,71 R.

В прямоугольной диметрии (рис. 85, 6) по осям х’ и z’ коэффициент искажения равен 7, по оси у-0,5. Поэтому на оси х’ откладываем радиус R. Остальные размеры определяем при помощи треугольника пропорциональности для диметрии. На натуральной шкале (1:1) откладываем радиус R и через точку А и конец этого отрезка проводим проецирующий луч. На шкале 0,5 получаем размер 0,57? для оси у на шкале 0,35 — размер 0,357? малой полуоси эллипса, который откладываем на z’. Размер 1,067? большой полуоси берём со шкалы 1,06 и откладываем его на прямой, перпендикулярной z’.

Полученные восемь точек в обоих случаях предпочтительнее соединить при помощи лекала.

Примечание. Размеры осей эллипса для прямоугольной изометрии можно определить и графически (рис. 86). Для этого из концов С и D взаимно перпендикулярных диаметров окружности проводим дуги радиусом CD до взаимного пересечения в точках А и В. Соединив точки А и В, получим большую ось эллипса, равную 1,22D, а отрезок CD будет его малой осью, равной 0,7 Ш.

Способ 2. Коробовая кривая. Коробовая кривая является циркульной кривой, состоящей из четырёх дуг окружностей (рис. 87). Ею можно заменить эллипс. Строится она по его осям.

На рис. 87 коробовая кривая построена в прямоугольной изометрии. Малая ось CD направлена вдоль аксонометрической оси z большая АВ ей перпендикулярна. Построение выполняем в определённой последовательности.

• Соединяем концы большой и малой полуосей (отрезок A Q.
• Находим разность большой и малой полуосей (отрезок СЕ). Для этого из центра О‘ радиусом О’А проводим дугу до пересечения с прямой, проходящей через CD, в точке Е.
• Откладываем СЕ от точки С на АС. Получаем точку F.
• Строим срединный перпендикуляр к отрезку AF и отмечаем точки пересечения его с прямыми линиями, проходящими через оси эллипса. 0 и 0₂ — центры двух дуг окружностей.

На рис. 88 построена прямоугольная диметрия окружности в плоскости x’O’z’ в виде коробовой кривой. Малая ось CD направлена вдоль оси у’ и равна 0,95D. Большая ось АВ ±у’ и равна 1,060. Последовательность построения та же, что была рассмотрена выше для изометрии.

Этот метод является универсальным и может применяться не только для построения аксонометрии окружности, но и любого эллипса или овала, если известны размеры его большой и малой оси, чем широко пользуются при конструировании технических деталей.

Способ 3. Овал. Построим прямоугольную изометрию окружности в плоскости х’О’у’, заменяя эллипс овалом (рис. 89)

Задаём аксонометрические оси х’, у’, z’ и направление большой оси эллипса (перпендикулярно z’). Из центра эллипса проводим окружность радиусом, равным радиусу той окружности, аксонометрию которой строим. На пересечении этой окружности с направлением малой оси эллипса (осью z’) получаем два центра дуг 0 и 0₂. Проводим прямые через 0 и точки Е, L (или через 0₂ и точки К, F) пересечения окружности с осями х’, у’. На пересечении их с направлением большой оси получаем ещё два центра — 0₃ и 0₄. Затем последовательно проводим из центра 0 дугу EL радиусом 0Е, из центра 0₄ — дугу LF радиусом Оф?, из 0₂ — дугу FK радиусом 0₂F, из 0₃ — дугу КЕ радиусом 0₂К. Построенный овал неточно повторяет форму эллипса. У них имеются небольшие расхождения в размерах. Таким приёмом можно построить овал только в прямоугольной изометрии.

На рис. 90 показано построение овала, заменяющего эллипс в прямоугольной диметрии. Овал строится по осям и пригоден только для эллипсов, у которых малая ось в три раза меньше большой оси (в плоскостях х’О’у’иг’ОУ). Рассмотрим построение овала в плоскости х’О’у’.

Проводим две взаимно перпендикулярные прямые. Одну вертикально (параллельно z% другую горизонтально. Точка пересечения прямых будет центром О эллипса. Отрезки АВ и CD — соответственно большая и малая ось эллипса. По обе стороны от центра О на прямой, проходящей через малую ось CD, откладываем отрезки, равные длине большой оси АВ эллипса. Получаем центры 0 и 0₂ двух дуг окружностей. Центры 0₃ и 0₄ двух других дуг окружностей удалены от концов А и В большой оси эллипса на расстояние 1/4CD. Соединяем попарно центры и между линиями центров проводим дуги: из 0 радиусом Оф, из 0₄ радиусом О4В, из 0₂ радиусом 0₂С, из 0₃ радиусом 6М. Как следует из построений, радиусы сопрягающихся дуг равны R = АВ + 1/2CD, г = 1/4CZ).

Коробовая кривая и овал представляют собой кривые, приближенные к эллипсу. Существуют и другие способы построения эллипса.

Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

План-конспект урока по черчению на тему «Понятие о лекальных и циркулярных кривых, построение овала и эллипса»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

План урока по черчению

Тема: Построение овала, эллипса.

Образовательная: сформировать знания учащихся по новой теме, научиться строить овал и эллипс;

Развивающая: развивать аккуратность, эстетический вкус, развивать познавательный интерес и интеллект у учащихся, а так же навыки черчения;

Воспитательная: воспитывать бережное отношение к предметам и приспособлениям, воспитывать чувство взаимопомощи, дисциплинированность, воспитывать усидчивость, прилежность и самостоятельность.

Тип урока: комбинированный

Программное дидактическое оснащение : учебник по черчению, чертежные инструменты, доска.

1. Организационный момент (2-3 мин);

2. Повторение пройденного материала (3 мин);

3. Изучение нового материала (10 мин);

4. Практическая работа (20 мин);

5. Подведение итогов. Рефлексия (3 мин);

6. Домашнее задание (2 мин).

Приветствие. Проверка отсутствующих, наличия учебных принадлежностей.

Повторение пройденного материала.

Прежде чем мы начнем изучать новую тему, давайте повторим тему прошлых уроков. Ответьте на следующие вопросы:

1.)Что такое сопряжение? (Сопряжение — плавный переход одной линии в другую)

2)Что такое касательная к окружности? (Прямая называется касательной к окружности, если она имеет только одну общую точку с этой окружностью).

Изучение нового материала.

Некоторые детали машин, инструменты для обработки металлов имеют контуры, ограниченные замкнутыми кривыми линиями, состоящими из взаимносопрягающихся дуг окружностей различных диаметров.

Коробовыми кривыми называются кривые, образованные сопряжением дуг окружностей. К таким кривым относятся овалы, овоиды, завитки.

Овал- замкнутая коробовая кривая, имеющая две оси симметрии.

Построить овал можно двумя способами, в зависимости от изначально заданных параметров.

1 способ: когда задается ширина и высота овала.

2 способ: когда задается только ширина овала.

Рассмотрим 1 способ построения овала

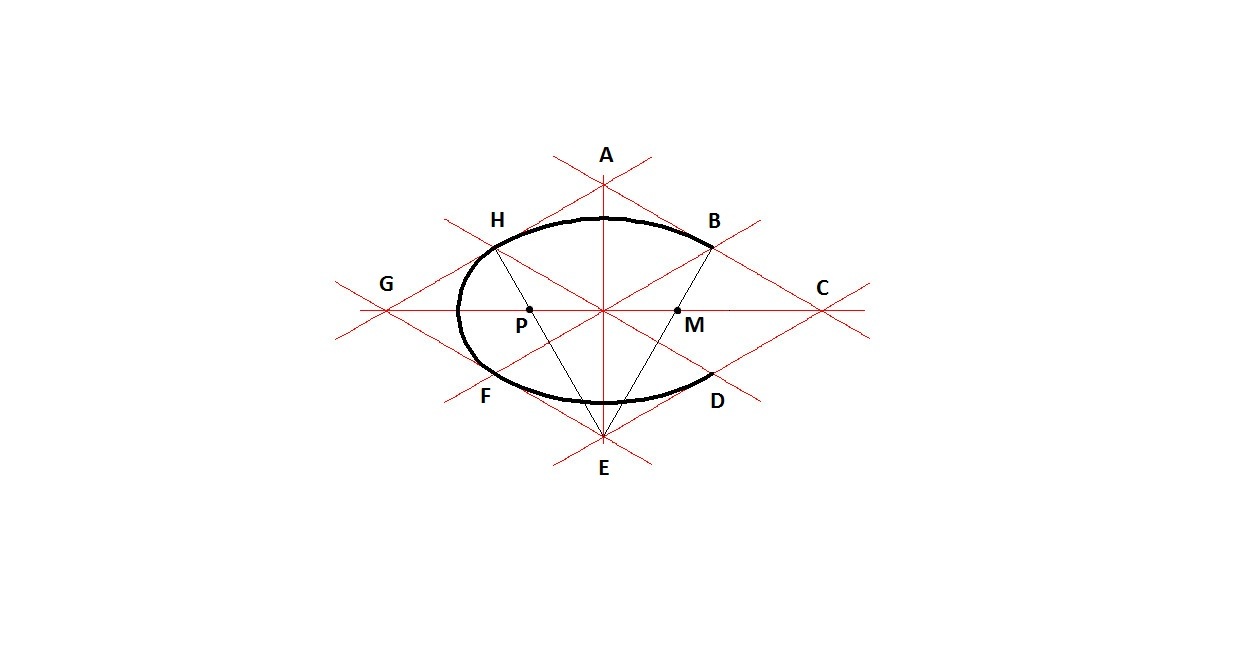
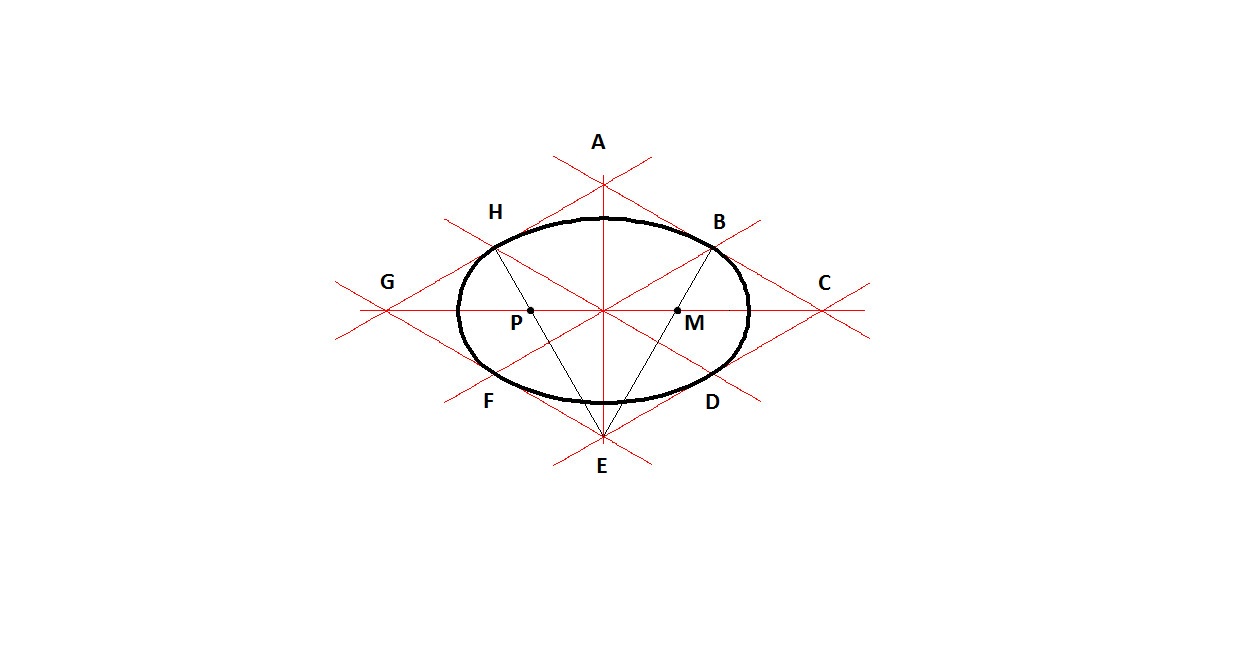
Построение овала по двум заданным осям симметрии (большей и меньшей) выполняется в следующей последовательности:

1. Проводим две оси симетрии, пересекающиеся под прямым углом.

2. На вертикальной оси отложим заданный нам размер ширины овала СD (по половине размера вверх и вниз из точки О). На горизонтальной оси таким же образом отложим длину овала АВ.

3. Соединяем прямой линией точки С и В.

4. Из центра О соединяем горизонтальную и вертикальную ось радиусом ОВ (намечаем точку е)

5. Из точки С проводим дугу радиусом Се до пересечения с наклонной прямой СВ (намечаем точку f).

6. Участок между точками f и B наклонной прямой делим на две равные части. Для этого из точки f проводим дугу радиусом fВ, затем из точки В проводим дугу того же радиуса, до пересечения с дугой, построенной ранее.

7. Соединяем точки пересечения дуг. Эта линия будет являться перпендикуляром к отрезку fВ и будет делить его пополам. Отмечаем точки пересечения построенной линии с горизонтальной и вертикальной осями симетрии (l и k).

8. Строим точку m симметричную точке l.

9. Строим точку n симметричную точке k.

10. Из точки k проводим прямую через точку m. Из точки n проводим прямые мерез точки m и l.

11. Радиусом равным расстоянию kC из точки k проводим дугу, соединяющую наклонные линии, исходящие из точки k. Тем же радиусом из точки n, как из центра, проводим дугу соединяющую наклонные линии исходящие из точки n.

12. Из точек m и l, как из центров, проводим дуги радиусом mA и замыкаем ими ранее проведенные дуги.

На этом построение овала можно считать за к онченым.

Овоид — замкнутая коробовая кривая,имеющая только одну ось симметрии.

Завиток — плоская спиральная кривая, вычерчиваемая циркулем путем сопряжения дуг окружностей.

Построение завитков выполняют при вычерчивании таких деталей, как пружины и спиральные направляющие.

Построение завитков выполняется из двух, трех и более центров и зависит от формы и размеров “глазка”, который может быть окружностью, правильным треугольником, шестиугольником и т.п.

При выполнении чертежей часто приходится прибегать к вычерчиванию кривых, состоящих из ряда сопряженных частей, которые невозможно провести циркулем. Такие кривые строят обычно по ряду принадлежащих им точек, которые затем соединяют плавной линией сначала от руки карандашом, а затем обводят при помощи лекал.

Рассматриваемые лекальные кривые располагаются в одной плоскости и называются поэтому плоскими.

Лекальные кривые широко применяются в машиностроении для очертания различных технических деталей, например: кронштейнов, ребер жесткости, кулачков, зубчатых колес, фасонного инструмента и т.п.

К лекальным кривым относят эллипс, параболу, гиперболу, циклоиду, эпициклоиду, эвольвенту, синусоиду, спираль Архимеда и др.

Эллипс — замкнутая плоская кривая, сумма расстояний каждой точки которой до двух данных точек(фокусов), лежащих на большой оси, есть величина постоянная и равная длине большой оси.

Широко применяемый в технике способ построения эллипса по большой(АВ) и малой(СD) осям.

Проводят две перпендикулярные осевые линии. Затем от центра О откладывают вверх и вниз по вертикальной оси отрезки, равные длине малой полуоси, а влево и вправо по горизонтальной оси-отрезки, равные длине большой полуоси.

Из центра О радиусами ОА и ОС проводят две концентрические окружности и ряд лучей-диаметров. Из точек пересечения лучей с окружностями проводят линии, параллельные осям эллипса, до взаимного пересечения в точках, принадлежащих эллипсу. Полученные точки соединяют от руки и обводят по лекалу.

Построение эллипса вписанного в ромб

Вначале строят ромб со стороной, равной диаметру изображаемой окружности. Для этого через точку О проводят изометрические оси x и y .

На них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки а, b , с, d проводят прямые параллельные осям; получают ромб.

Большая ось овала располагается на большой диагонали ромба.

После этого вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги.

Их радиус R равен расстоянию от вершины тупого угла (точек А и В) до точек а, b или с,d соответственно.

Через точки B и a , B и b проводят прямые. В пересечении прямых Ba и В b с большей диагональю ромба находятся точки C и D . Эти точки будут центрами малых дуг. Их радиус R , равен С a (или Db ).

Дугами этого радиуса плавно соединяют большие дуги овала.

Для решения некоторых проблем не всегда достаточно глубокого анализа. Иногда умную мысль легче выловить в бушующем море идей, нежели из ровной поверхности размеренной задумчивости. В этом случае оправдано применение техники мозгового штурма, цель которой – быстро найти верное решение.

Упражнение 1. Циркульные кривые.

Работаем в паре с соседом по парте, задание: найти другие способы построения овалов.

Упражнение 2. Лекальные кривые.

Цель задания. Научиться чертить лекальную кривую – эллипс (со сторонами 60мм;30мм)

Подведение итогов. Рефлексия.

Учесть правильность и качество выполненной работы.

д/з: Откройте дневники и запишите домашнее задание: §1.11+ построение в тетради (Выполнить чертеж предмета, форма которого образована на основе циркульных и лекальных кривых (машиностроительной детали, плоской игрушки, ювелирного изделия и т.п.).)