Как построить объемную окружность

Как построить окружность?

Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.

Радиусом называется любой отрезок соединяющей точку окружности с ее центром.

Чтобы построить окружность необходимо знать уравнение окружности:

(х – а) 2 + (у – b) 2 = R 2

Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.

И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:

Пример №1:
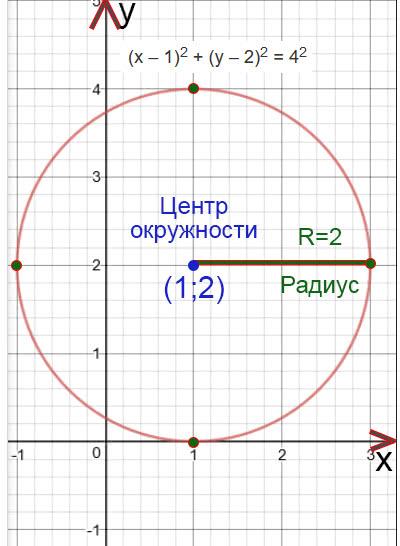
(х – 1) 2 + (у – 2) 2 = 4 2

Найдем центр окружности:
х – 1=0
x=1

Центр окружности будет находится в точке (1;2)

Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2

Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.

Пример №2:
х 2 + (у + 1) 2 =1

Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2

Найдем центр окружности:
х=0

Центр окружности будет находится в точке (0;–1)

Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1

Построим окружность.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Видео:Видеоуроки по КОМПАС 3D. Урок 1 Деление окружности на равные частиСкачать

Чертеж круга, построение окружности в изометрии, формулы

Чертеж круга, построение окружности в изометрии прямоугольной по всем трем осевым направлениям X, Y, Z уменьшаются на восемнадцать процентов. По ГОСТу рекомендуют строить изометрическую проекцию по осям без сокращения. При таком построении происходит увеличение изображений в одну целую двадцать две сотых раза.

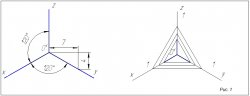
Посмотрим на 1-ый рисунок, как правильно располагать оси координат и наносить штриховку в прямоугольной изометрии.

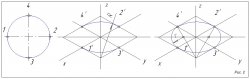
На 2-ом рисунке посмотрим как правильно построить изометрическую проекцию окружности.

Если строим проекцию без искажения по трем осям X, Y, Z, значит большая ось эллипсов будет равняться 1,22, а малая – 0,71. Если строим проекцию с искажениями по трем осям X, Y, Z, значит большая ось эллипсов будет равняться диаметру (D), а малая – 0,58D.

На 3-ем рисунке показано как правильно располагать окружность на чертеже.

Чертеж круга и окружности.
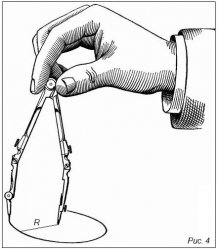
Основным геометрическим размер окружности является прямой отрезок, который соединяет ее центр с точкой.

Условное обозначение R. Название радиус.

Смотрим 4-ый рисунок.

Множество точек, одинаково удаленных от центра на расстояние R описывают замкнутую плоскую кривую, которая и называется окружность.

Диаметр окружности обозначается D
D = 2R

Длина окружности обозначается С
С = 2πR = πD

π=С/D=3,141 592 653 589 793 … (трансцендентное число)

Множество точек, удаленных от центра на расстояние не превышающее R, называется кругом.

Площадь круга обозначается S
S = πR² = πD²/4

Вспомогательные формулы
С = 2√πS ≈ 3,545√S ≈ 3,142D
S = CD/4 ≈ 3,142 R² ≈ 0,785 D² ≈ 0,25CD
R = C/2π ≈ 0,159C
D = 2√S/π ≈ 1,128√S

Дополнительную информацию по геометрии смотрим на страницах сайта

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Как построить объемные фигуры

В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.

Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).

Однако, бумага имеет и ряд характерных особенностей:

• капризный, хрупкий материал
• требует высокой аккуратности, внимательности, усидчивости при работе

По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.

В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.

Вам понадобятся следующие материалы:

• лист бумаги
• карандаш
• линейка
• ластик
• ножницы
• клей ПВА либо клеящий карандаш
• кисточка для клея, лучше из жесткой щетины
• циркуль (для некоторых фигур)

Видео:Как Сделать Окружности по Кругу в Компасе ► Уроки Компас 3DСкачать

Как сделать куб из бумаги?

Куб – правильный многогранник, каждая грань которого представляет собой квадрат

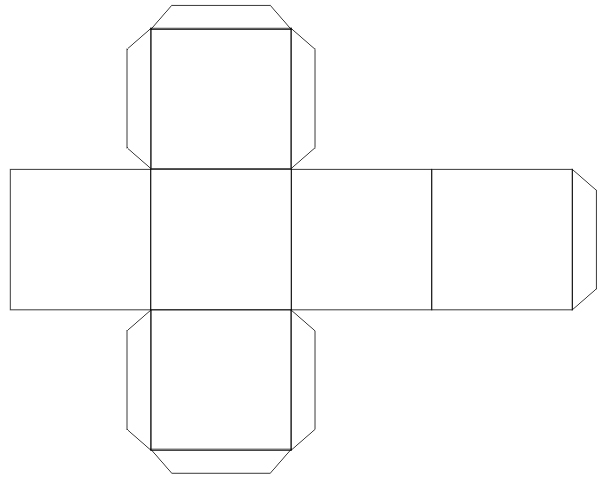
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.

1. Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
2. Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу.
3. Над и под любыми из квадратов рисуем по одному такому же квадрату.
4. Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
5. Куб готов!

После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!

Видео:Построение эвольвенты окружностиСкачать

Как сделать конус из бумаги?

Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.

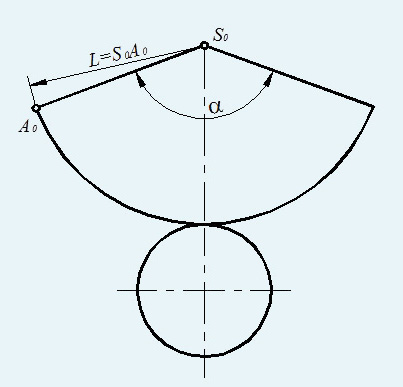
1. Рисуем циркулем окружность
2. Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
3. Склеиваем боковую поверхность конуса.
4. Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
5. Приклеиваем основание к боковой поверхности.
6. Конус готов!

Видео:Построение пятиугольника циркулемСкачать

Как сделать цилиндр из бумаги?

Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

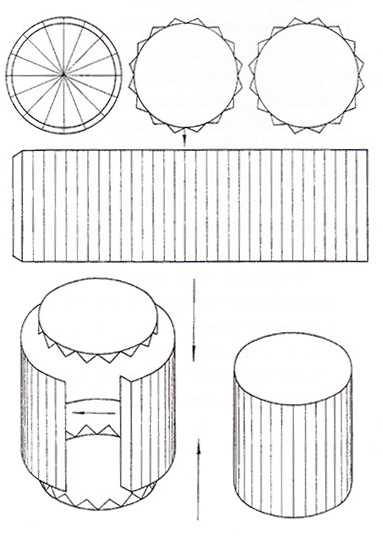
1. Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
2. Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
3. Вырезаем все детали будущего бумажного цилиндра.
4. Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
5. Цилиндр готов!

Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Как сделать параллелепипед из бумаги?

Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.

1. Выбираем размеры параллелепипеда и величины углов.
2. Чертим параллелограмм — основание. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
3. Вырезаем развертку и склеиваем.
4. Параллелепипед готов!

Видео:1 2 4 сопряжение окружностейСкачать

Как сделать пирамиду из бумаги?

Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.

1. Выбираем размеры пирамиды и количество ее граней.
2. Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
3. От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
4. Вырезаем и склеиваем фигуру.
5. Пирамида готова!

• фигуры из бумаги
• пирамида
• куб
• конус
• цилиндр
• параллелепипед

Большой выбор развёрток простых геометрических фигур.

Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.

Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.

Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.

Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.

Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂

А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.

Развёртки трёхгранной пирамиды на первом листе для печати.

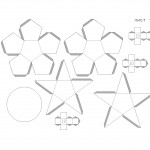
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.

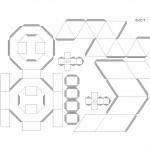
Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.

Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.

Развёртки пятигранника на втором листе.

Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.

А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.

Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.

Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.

Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.

Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.

Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.

Довольно интересная фигура – ромб, её детали на третьем листе.

А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.

Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.

Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.

И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.

На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!

КОММЕНТАРИИ

Задали по геометрии: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Тетраэдр, куб и додекаэдр сделала, а вот оставшиеся две никак(((
Еще возникли трудности с склеиванием..

спасибо, хз че бы делал еслиб не этот сайт =»)

Спасибо большое!)))) очень выручили!

Я бы и так не смогла, полезно было ознакомиться.

помогите, как сделать развертку Четырёхугольной пирамиды с основанием — ромб

Как сделать развёртку тора (то есть кольца, вернее, его поверхности)?
Вопрос задан с практической целью, хочу самостоятельно обшить руль машины кожей, но для этого необходимо начертить выкройку, вот тут и возникла трудность — не хватает воображения всё это нарисовать, ведь поверхность тора — это т.н. неразвёртываемая поверхность (вернее, условно-развёртываемая).
Люди, помогите советом или ссылкой, плиз!

Я бы вам посоветовал сходить в магазин и посмотреть как сшиты подобные чехлы для автомобильного руля. Вообще кожа специфический материал, с ней можно делать практически всё, из бумаги такого не сделаешь, поэтому и выкройти тут трудно посоветовать, лучше посмотреть как это уже сделано и дома подумать как сделать своё.

как сделать усечённую пирамиду

Спасибо за информацию,но не все фигуры изображены.Пошли в 9 класс ,но не в РОссии.Необходима помощь. С уважением,Тамара.

Может глупый вопрос, но как сделать из бумаги шар? т.е. не просто круг, а именно объемный шар? есть ли вообще в природе такая развертка?

Развёртка шара из бумаги представляет собой дольки, полоски бумаги сужающиеся по краям. Развёртка шара похожа на рисунок из полосок на арбузе.

Дмитрий, это я тоже помню из курса школьной географии 🙂
А вот как сделать из атласа в электронном виде шар в электронном виде, чтобы потом распечатать и наклеить?

Почему не указаны параметры? Длина, ширина и т.д.?

как сделать цилиндр из бумаги помамогите плиз

Большое человеческое СПАСИБО.

Спасибо вам огромное! Очень нужен был конус. Теперь, благодаря вам, я знаю, как его сделать))

фу
дану это проче простого ещебы квадраты делать учили

мне по технологие задали это

спасибо большое. по геометрии 3 выходит а так 4 :DDD

плохо не чё не пойму

развертка паллалеллограмма неправильная 5 лист

можно было бы еще акуратнее , как-то грубо

шар не получился там не правильный чертеж

Спасибо большое)))) Ну очень помогли)))

Велике спасибі.Розгортки допомогли мені при виготовленні геометричних фігур на технологіях.

Спасибо большое, хорошие и удобные развёртки)
Проблема с параллелепипедом на пятом листе решается отрезанием косячной грани и её разворотом в правильную сторону)

Развертка фигур. Может развертка геометрических тел?

красиво можно научиться

thank you very much

Спасибо большое! Ребенку во втором класе уже задали эти фигуры. Спасибо Вам за модели, очень удобно, распечатали, сидит, клеит )

Модели конечно интересные, но люди парятся выполняя их, хотя особо труда не составило мне сделать даже сферу. Сыновьям моим (близнецам) задали сделать фигурки из картона, но я то заканчил политех и по начерталке и проходили развертки этих фигур. А у кого гуманитарное образование? Вот у них то и проблемма.

Полезно для изо в 6 классе

Мне кажется, что у Вашего шестигранника восемь граней, а у пятигранника — семь. И называются эти тела либо призмами, либо усеченными пирамидами( в зависимости от соотношения оснований)

Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Также на этой странице вы найдете плоские фигуры для вырезания, из которых нужно сложить замок. Этот учебный материал поможет ребенку наглядно изучить объемные геометрические фигуры: куб, пирамиду, ромб, шестигранник, цилинд и конус. Задание развивает наглядно-образное мышление.

Видео:Построение окружности по трём точкам.Скачать

Объемные геометрические фигуры из бумаги — Вырезаем и клеим:

Здесь вы можете скачать объемные геометрические фигуры из бумаги в виде разверток, которые необходимо распечатать на принтере, вырезать и склеить по указанным местам. В результате у вас получатся объемные фигуры: куб, пирамида (трехгранная и четырехгранная), ромб, шестиугольник, конус и цилиндр. На каждой развертке написано название фигуры, чтобы ребенок во время работы всегда мог видеть, какую фигуру он делает. Это очень удобно для обучения, так как дети обычно не любят, когда взрослые по несколько раз повторяют одно и то же. А в этом случае у родителей нет необходимости проговаривать вслух названия фигур.

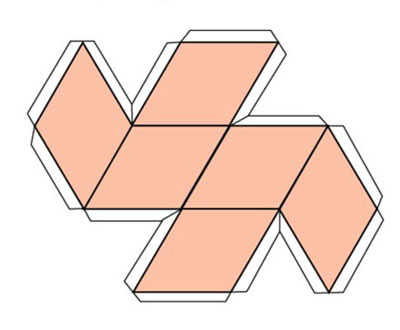
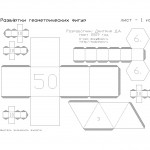
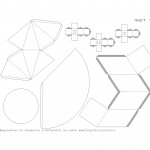
• Итак, в первом листе мы выложили следующие геометрические фигуры: куб (фигура, поверхность которого состоит из 6 квадратов), трехгранная пирамида (основание пирамиды и 3 грани), четырехгранная пирамида (основание и 4 грани), ромб (фигура, визуально состоящая из двух пирамид, имеющих общее основание).
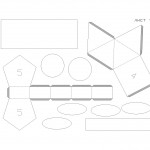
• Во втором листе вы найдете развертки таких геометрических фигур из бумаги: шестигранник (фигура, состоящая из шести граней), цилиндр (состоящий из свернутого прямоугольника и двух окружностей-оснований) и конус.

Скачать геометрические фигуры из бумаги — развертки для вырезания вы можете во вложениях внизу страницы

Скачайте и распечатайте 2 листа с фигурами, вырежьте их аккуратно ножницами и склейте в нужных местах. Учтите, что у бумажных фигур есть дополнительные места для сгиба и склеивания (у нас они выделены оранжевым цветом). Все оранжевые места вам необходимо согнуть и намазав их клеем вклеить с внутренней стороны фигуры.

После того, как дети, при помощи взрослых, склеят все геометрические фигуры из бумаги, можно продолжить занятие, задавая детям вопросы. Например: «Покажи мне пирамиду. Сколько у нее сторон? Где ее основание? Чем эта пирамида (показываете трехранную) отличается от этой (четырехранной)? Покажи мне цилиндр. Какие предметы он тебе напоминает? Покажи конус. На что он похож? Покажи куб. Сколько у него сторон? Из какой геометрической фигуры состоят его стороны?» — и так далее.

В зависимости от возраста ребенка, можно использовать в занятии различные обучающие материалы. Например, что такое пирамида:

Какие бывают пирамиды. (Пусть ребенок покажет из них те, которые он склеил)

Что такое конус и цилиндр. На что они похожи:

Можете также скачать эти обучающие картинки во вложениях.

Плоские геометрические фигуры из бумаги — Строим замок

В этом упражнении вы можете скачать плоские геометрические фигуры из бумаги и построить из них замок, то есть выложить их на столе таким образом, чтобы получился заданный силуэт замка. Для начала скачайте во вложениях бланки с заданием и распечатайте на принтере. Затем вырежьте геометрические фигуры (квадрат, трапеция, полукруг и треугольник), которые даны к этому заданию. Все карточки с заданиями даны с увеличением уровня сложности (от 1 до 6 задания).

Все карточки с замками можно распечатывать на обычной офисной белой бумаге. А геометрические фигуры нужно распечатать на цветном картоне. Если нет цветного картона, можно использовать для распечатки цветную бумагу, а затем наклеить бумагу на лист картона и вырезать фигуры.

После этого подробно объесните ребенку инструкцию к выполнению упражнения.

«Строители, прежде чем строить какое-либо здание, смотрят сначала на его чертеж или схему, в которых показано каким оно должно быть. Такие чертежи бывают разными. Вот например, один из них», — взрослый показывает одну или две игровых схемы замка с нашего задания. — «Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.» — взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.

Очень важно начинать занятие, не используя подсказки, то есть нужно закрывать от ребенка геометрические фигуры, которые нарисованы рядом с силуэтом каждого замка. Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.

Также не нужно допускать, чтобы ребенок накладывал вырезанные геометрические фигуры из бумаги на силуэт замка, так как при этом он не будет развивать наглядно-образное мышление. Старайтесь, чтобы всю основную работу ребенок проводил в уме, а не методом подбора.

Скачать карточки с плоскими геометрическими фигурами для строительства замка вы можете во вложениях внизу страницы.

Геометрические фигуры для вырезания:

Также вам будут полезны и другие материалы по изучению геометрических фигур:

Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических формю

Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.

Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.

Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.

Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.

Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.

Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии

Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.

И еще можете поиграть в математические игры онлайн от лисенка Бибуши:

В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.

💡 Видео

Построить описанную окружность (Задача 1)Скачать

Окружность. 7 класс.Скачать

Как нарисовать пятиконечную ЗВЕЗДУ с помощью циркуляСкачать

Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Как рисовать "Штриховку" - А. Рыжкин [ENG SUB]Скачать

Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Короткие загадки, которые осилит не каждый профессорСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Построение шестнадцатиугольника циркулемСкачать

Как Сделать Окружность в Компасе ► Уроки Компас 3DСкачать