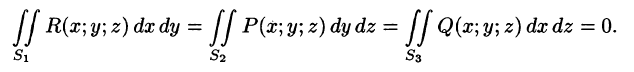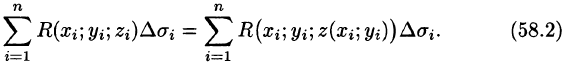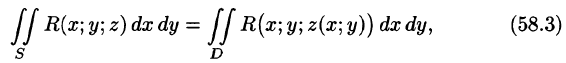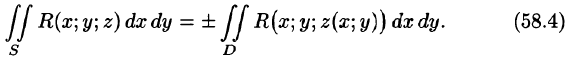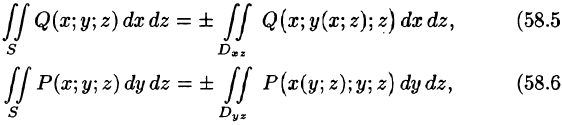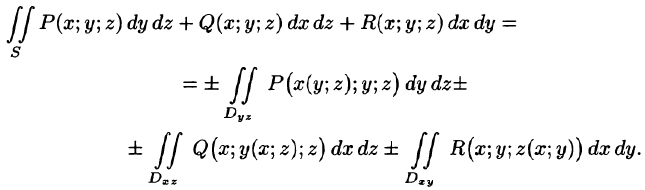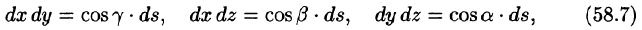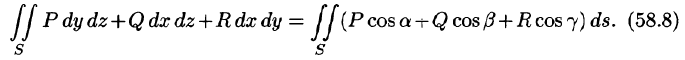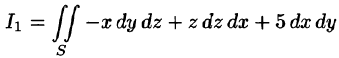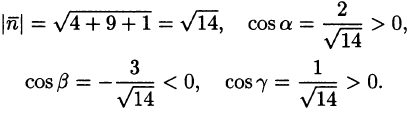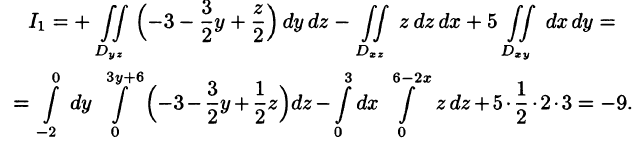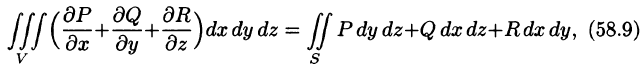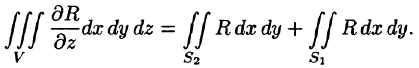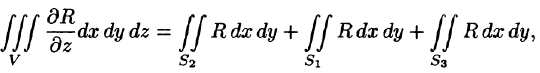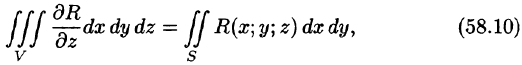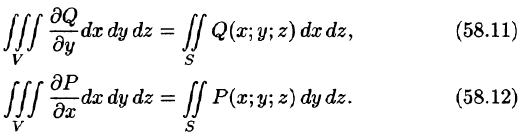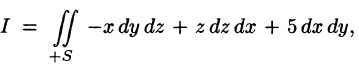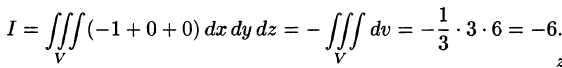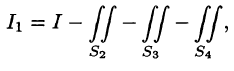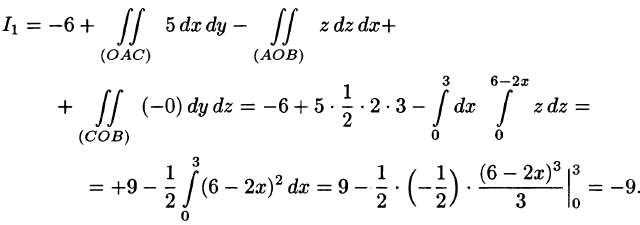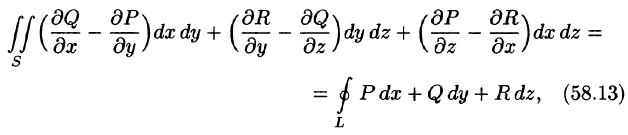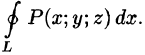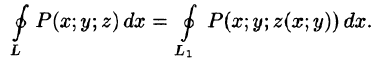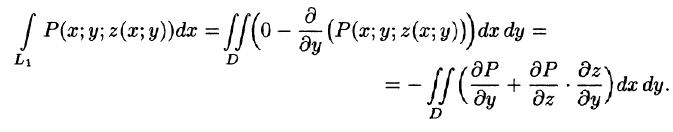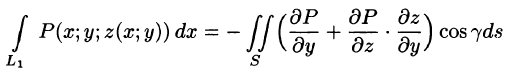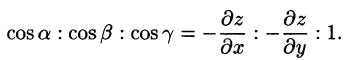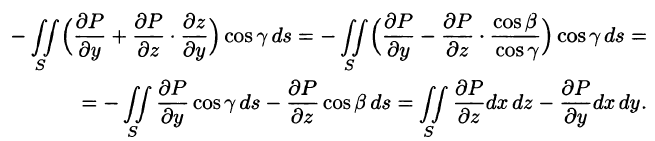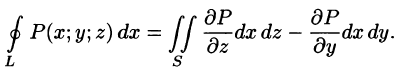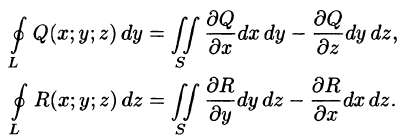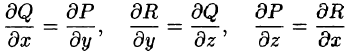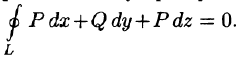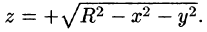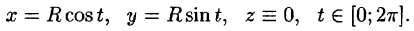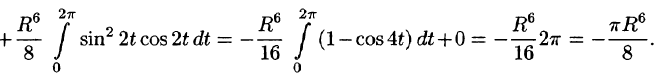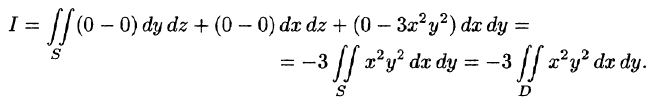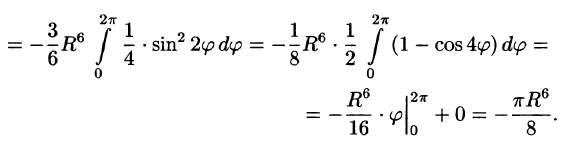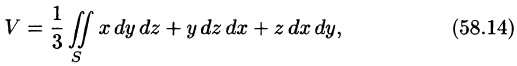- Понятие криволинейного интеграла
- Криволинейные интегралы первого рода
- Криволинейные интегралы второго рода
- Вычисление криволинейных интегралов первого рода
- Кривая дана в декартовых прямоугольных координатах
- Кривая дана в параметрической форме
- Вычисление криволинейных интегралов второго рода
- Кривая дана в декартовых прямоугольных координатах
- Кривая дана в параметрической форме
- Больше примеров вычисления криволинейных интегралов
- Вычисление длины дуги кривой
- Вычисление площади участка плоскости
- Вычисление площади цилиндрической поверхности
- Вычисление массы материальной кривой
- Определение статических моментов материальной кривой
- Вычисление моментов инерции материальной кривой
- Вычисление координат центра тяжести материальной кривой
- Вычисление работы силы
- Поверхностные интегралы в математике с примерами решения и образцами выполнения
- Поверхностный интеграл первого рода
- Интеграл по цилиндрической поверхности
- Интеграл по сферической поверхности
- Определение и свойства поверхностных интегралов
- Поверхностный интеграл I рода
- Вычисление поверхностного интеграла I рода
- Некоторые приложения поверхностного интеграла I рода
- Площадь поверхности
- Масса поверхности
- Моменты, центр тяжести поверхности
- Поверхностный интеграл II рода
- Вычисление поверхностного интеграла II рода
- Формула Остроградского-Гаусса
- Формула Стокса
- Некоторые приложения поверхностного интеграла II рода
- Интеграл по окружности пример
- Контакты
- 🎬 Видео
Видео:Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать

Понятие криволинейного интеграла
Криволинейные интегралы — обобщение понятия определённого интеграла на случай, когда областью интегрирования является отрезок некоторой кривой, лежащий в плоскости. Общая запись криволинейного интеграла следующая:
где f(x, y) — функция двух переменных, а L — кривая, по отрезку AB которой происходит интегрирование. Если подынтегральная функция равна единице, то криволинейный интеграл равен длине дуги AB.
Как всегда в интегральном исчислении, криволинейный интеграл понимается как предел интегральных сумм каких-то очень маленьких частей чего-то очень большого. Что же суммируется в случае криволинейных интегралов?
Пусть на плоскости расположен отрезок AB некоторой кривой L, а функция двух переменных f(x, y) определена в точках кривой L. Пусть мы выполняем с этим отрезком кривой следующий алгоритм.
- Разделить кривую AB на части точками (рисунки ниже).
- В каждой части свободно выбрать точку M.
- Найти значение функции в выбранных точках.
- Значения функции умножить на
- длины частей в случае криволинейного интеграла первого рода;
- проекции частей на ось координат в случае криволинейного интеграла второго рода.
- Найти сумму всех произведений.
- Найти предел найденной интегральной суммы при условии, что длина самой длинной части кривой стремится к нулю.
Если упомянутый предел существует, то этот предел интегральной суммы и называется криволинейным интегралом от функции f(x, y) по кривой AB.
Случай криволинейного интеграла
первого рода
Случай криволинейного интеграла
второго рода
Введём следующие ообозначения.
M i (ζ i ; η i ) — выбранная на каждом участке точка с координатами.
f i (ζ i ; η i ) — значение функции f(x, y) в выбранной точке.
Δs i — длина части отрезка кривой (в случае криволинейного интеграла первого рода).
Δx i — проекция части отрезка кривой на ось Ox (в случае криволинейного интеграла второго рода).
d = maxΔs i — длина самой длинной части отрезка кривой.
Криволинейные интегралы первого рода
Исходя из вышеизложенного о пределе интегральных сумм, криволинейный интеграл первого рода записывается так:

Криволинейный интеграл первого рода обладает всеми свойствами, которыми обладает определённый интеграл. Однако есть одно важное различие. У определённого интеграла при перемене местами пределов интегрирования знак меняется на противоположный:

В случае же криволинейного интеграла первого рода не имеет значения, какую из точек кривой AB (A или B) считать началом отрезка, а какую концом, то есть

Криволинейные интегралы второго рода
Исходя из изложенного о пределе интегральных сумм, криволинейный интеграл второго рода записывается так:

В случае криволинейного интеграла второго рода при перемене местами начала и конца отрезка кривой знак интеграла меняется:

При составлении интегральной суммы криволинейного интеграла второго рода значения функции f i (ζ i ; η i ) можно умножать также на проекции частей отрезка кривой на ось Oy. Тогда получим интеграл

На практике обычно используется объединение криволинейных интегралов второго рода, то есть две функции f = P(x, y) и f = Q(x, y) и интегралы

а сумма этих интегралов
называется общим криволинейным интегралом второго рода.
Видео:Вычислить интеграл по заданному контуру. Интегрирование по части окружности и по отрезку прямой.Скачать
Вычисление криволинейных интегралов первого рода
Вычисление криволинейных интегралов первого рода сводится к вычислению определённых интегралов. Рассмотрим два случая.
Кривая дана в декартовых прямоугольных координатах
Пусть на плоскости задана кривая y = y(x) и отрезку кривой AB соответствует изменение переменной x от a до b. Тогда в точках кривой подынтегральная функция f(x, y) = f(x, y(x)) («игрек» должен быть выражен через «икс»), а дифференциал дуги 

Если интеграл проще интегрировать по y, то из уравнения кривой нужно выразить x = x(y) («икс» через «игрек»), где 

Пример 1. Вычислить криволинейный интеграл

где AB — отрезок прямой между точками A(1; −1) и B(2; 1) .
Решение. Составим уравнение прямой AB , используя формулу 

Из уравнения прямой выразим y через x :

Тогда 
Кривая дана в параметрической форме
Пусть в пространстве задана кривая
Тогда в точках кривой функцию нужно выразить через параметр t (

Аналогично, если на плоскости задана кривая

то криволинейный интеграл вычисляется по формуле

Пример 2. Вычислить криволинейный интеграл

где L — часть линии окружности

находящаяся в первом октанте.
Решение. Данная кривая — четверть линии окружности, расположенная в плоскости z = 3 . Она соответствует значениям параметра 

то дифференциал дуги
Подынтегральную функцию выразим через параметр t :

Теперь, когда у нас всё выражено через параметр t , можем свести вычисление данного криволинейного интеграла к определённому интегралу:
Видео:ТФКП. ИНТЕГРАЛ ПО ДУГЕ ОКРУЖНОСТИ от неаналитической функции. Метод замены переменной.Скачать

Вычисление криволинейных интегралов второго рода
Так же, как и в случае криволинейных интегралов первого рода, вычисление интегралов второго рода сводится к вычислению определённых интегралов.
Кривая дана в декартовых прямоугольных координатах
Пусть дана кривая на плоскости уравнением функции «игрек», выраженной через «икс»: y = y(x) и дуге кривой AB соответствует изменение x от a до b . Тогда в подынтегральную функцию подставим выражение «игрека» через «икс» и определим дифференциал этого выражения «игрека» по «иксу»: 
Аналогично вычисляется криволинейный интеграл второго рода, когда кривая дана уравнением функции «икс», выраженной через «игрек»: x = x(y) , 
Пример 3. Вычислить криволинейный интеграл

а) Вычислим криволинейный интеграл по отрезку прямой (на рисунке — синяя). Напишем уравнение прямой и выразим «игрек» через «икс»:

Получаем dy = dx . Решаем данный криволинейный интеграл:
б) если L — дуга параболы y = x² , получим dy = 2xdx . Вычисляем интеграл:
В только что решённом примере получили в двух случаях один и тот же результат. И это не совпадение, а результат закономерности, так как данный интеграл удовлетворяет условиям следующей теоремы.
Теорема. Если функции P(x,y) , Q(x,y) и их частные производные 


Кривая дана в параметрической форме
Пусть в пространстве дана кривая


а в подынтегральные функции подставим

выражения этих функций через параметр t . Получаем формулу для вычисления криволинейного интеграла:
Пример 4. Вычислить криволинейный интеграл

если L — часть эллипса
отвечающая условию y ≥ 0 .
Решение. Данная кривая — часть эллипса, находящаяся в плоскости z = 2 . Она соответствует значению параметра 

можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:
Если дан криволинейный интеграл и L — замкнутая линия, то такой интеграл называется интегралом по замкнутому контуру и его проще вычислить по формуле Грина.
Видео:Формула ГринаСкачать

Больше примеров вычисления криволинейных интегралов
Пример 5. Вычислить криволинейный интеграл

где L — отрезок прямой 
Решение. Определим точки пересечения прямой с осями координат. Подставив в уравнение прямой y = 0 , получим 



Из уравнения прямой выразим y :



Теперь можем представить криволинейный интеграл в виде определённого интеграла и начать вычислять его:
В подынтегральном выражении выделяем множитель 
Пример 6. Вычислить криволинейный интеграл

где L — дуга параболы 
Решение. Так как 

Теперь можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:
Пример 7. Вычислить криволинейный интеграл

где L — дуга астроиды
в первом квадранте.
Решение. В первом квадранте 
Представляем криволинейный интеграл в виде определённого интеграла и вычисляем его:
Пример 8. Вычислить криволинейный интеграл

где L — первая арка циклоиды
Решение. Циклоида образует первую арку при изменении параметра t от 0 до 2π . Определим дифференциал дуги:

Подставим в криволинейный интеграл dl и y , выраженные через параметр t и получаем:
Пример 9. Вычислить криволинейный интеграл

где L — отрезок прямой от точки A(1; 1) до точки B(3; 5) .
Решение. Составим уравнение прямой AB :

Из полученного уравнения прямой выразим «игрек»:
Поэтому 
Пример 10. Вычислить криволинейный интеграл

где L — первая арка циклоиды
Решение. Из уравнений кривой следует

Так как циклоида образует первую арку при изменении параметра t от 0 до 2π , то получаем соответствующие пределы интегрирования. Решаем данный криволинейный интеграл:

Уравнением кривой M 0 M 1 является y = 1 , тогда dy = 0 , на кривой M 1 M x — константа, значит, dx = 0 . Продолжаем и завершаем решение:
Вычисление длины дуги кривой
Если подынтегральная функция равна единице, то криволинейный интеграл первого рода равен длине дуги кривой L:

Пример 12. Вычислить длину дуги кривой

где 
Решение. Составляем криволинейный интеграл первого рода:

Определим производную «игрека»:

Продолжаем и завершаем решение:
Вычисление площади участка плоскости
Если границей участка D плоскости является кривая L, то площадь участка D можно вычислить в виде криволинейного интеграла второго рода

Пример 13. Вычислить площадь участка плоскости, ограниченного эллипсом

Решение. Площадь участка плоскости можно вычислить как криволинейный интеграл второго рода

где L — замкнутая линия, ограничивающая участок. Так как

Вычисление площади цилиндрической поверхности
Пусть на плоскости xOy дана гладка кривая L, в точках которой определена непрерывная функция двух переменных 


Вычисление массы материальной кривой
Если L — материальная кривая с плотностью 
Определение статических моментов материальной кривой
Статические моменты материальной кривой с плотностью 


Вычисление моментов инерции материальной кривой
Моменты инерции материальной кривой с плотностью 



Вычисление координат центра тяжести материальной кривой
Координаты центра тяжести 



Вычисление работы силы
Если под воздействием переменной силы 

Пример 14. В каждой точке плоскости действует сила 

Решение. Работу силы вычислим как криволинейный интеграл второго рода

Используя уравнение параболы, производим замену переменной
Видео:Математический анализ, 48 урок, Криволинейные интегралы второго родаСкачать

Поверхностные интегралы в математике с примерами решения и образцами выполнения
При изучении темы «Поверхностные интегралы» вы познакомитесь с понятием интеграла по поверхности от функции трех
переменных и научитесь сводить его к двойному (а затем — к повторному), проецируя заданную поверхность на одну из координатных плоскостей. Кроме того, вы научитесь вычислять интегралы по части цилиндрической и сферической поверхностей.
Видео:ТФКП. Интегральная формула Коши. Примеры решений типовых задач. Решение контурных интегралов.Скачать

Поверхностный интеграл первого рода
Постановка задачи. Вычислить поверхностный интеграл
где 
и некоторыми неравенствами.
План решения. Поверхностный интеграл сводится к двойному
проецированием 
где D — проекция 
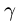
к поверхности 
Замечание:
Если уравнение F(x,y,z) = 0 не определяет однозначно функцию z = z(x,y), то проецируем 
также разбить поверхность на части и воспользоваться аддитивностью интеграла).
1.Единичные нормальные векторы 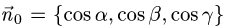
2.Проекцию D поверхности 

3.Находим z = z(x, у), решая уравнение F(x, у, z) = 0.
4.Переходим от поверхностного интеграла к двойному по формуле (1) и вычисляем двойной интеграл, сводя его к повторному.
Пример:
Вычислить поверхностный интеграл
где 
расположенная в первом октанте (т.е. 
Решение:
1.Единичные нормальные векторы 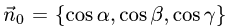
поверхности, заданной уравнением F(x, у, z) = 0, определяются формулой
В данном случае F(x,y,z) = х + 2у + 3z — 1. Следовательно,
2.Поверхность 
Ее проекцию D на плоскость XOY находим, исключая z из условий,
определяющих 
3.Из уравнения х + 2у + 3z — 1 = 0 находим z(x, у) = (1 — х — 2у)/3.
4.Переходим от поверхностного интеграла к двойному по формуле (1) и вычисляем двойной интеграл, сводя его к повторному:
Ответ.
Интеграл по цилиндрической поверхности
Постановка задачи. Вычислить поверхностный интеграл
где 
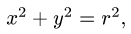
z = 0 и z = h.
1.Вводим на заданной поверхности (цилиндре) криволинейные
координаты
В этих координатах поверхность задается условиями
3.Вычисляем повторный интеграл и записываем ответ.
Пример:
Вычислить поверхностный интеграл
где 
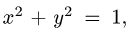
z = 0, z = 2.
Решение:
1.Вводим на заданной поверхности (цилиндре) криволинейные
координаты
В этих координатах поверхность задается условиями
2.Так как 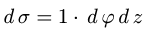
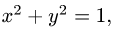
3.Вычисляем повторный интеграл:
Ответ.
Интеграл по сферической поверхности
Постановка задачи. Вычислить поверхностный интеграл
где 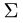
1.Вводим на заданной поверхности (сфере) криволинейные координаты
В этих координатах поверхность задается условиями
2.Так как 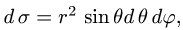
3.Вычисляем повторный интеграл и записываем ответ.
Пример:
Вычислить поверхностный интеграл
где 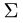
Решение:
1.Вводим на заданной поверхности (сфере) криволинейные координаты
В этих координатах поверхность задается условиями
2.Так как 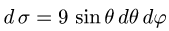
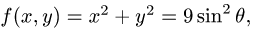
3.Вычисляем повторный интеграл:
Ответ.
Видео:Двойной интеграл в полярных координатахСкачать

Определение и свойства поверхностных интегралов




Видео:Криволинейный интеграл по длине дуги ➜ Криволинейный интеграл 1-го родаСкачать

Поверхностный интеграл I рода
Обобщением двойного интеграла является так называемый поверхностный интеграл.
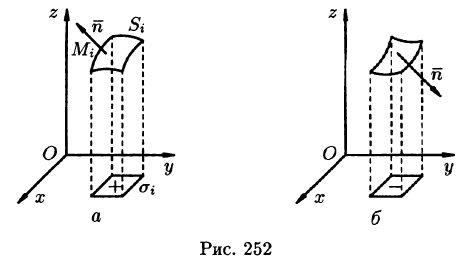
Пусть в точках некоторой поверхности S, с площадью S , пространства Oxyz определена непрерывная функция f(х; у; z). Разобьем поверхность S на п частей 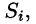
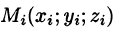
Она называется интегральной для функции f(x;y;z) по поверхности S.
Если при 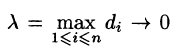
Таким образом, по определению,
Отметим, что «если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f(x;y;z) непрерывна на этой поверхности, то поверхностный интеграл существует» (теорема существования).
Поверхностный интеграл I рода обладает следующими свойствами:
3. Если поверхность S разбить на части 
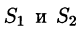
4.Если на поверхности S выполнено неравенство
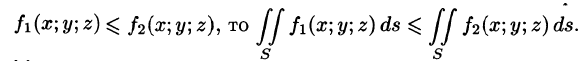
7.Если f(x; у, z) непрерывна на поверхности S, то на этой поверхности существует точка 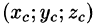
(теорема о среднем значении).
Видео:Демидович №4367: интеграл по окружностиСкачать

Вычисление поверхностного интеграла I рода
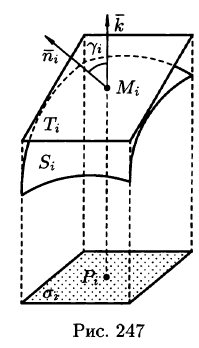
Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области D — проекции поверхности S на плоскость Оху.
Разобьем поверхность S на части 
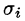
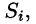
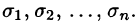
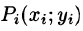
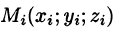

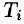
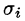
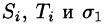
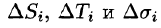

Обозначив через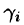
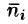
(область 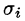
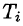
Если поверхность S задана уравнением z = = z(x;y), то, как известно (см. (45.2)), уравнение касательной плоскости в точке 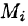
где 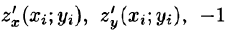
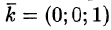
Равенство (57.4) принимает вид
В правой части формулы (57.2) заменим 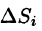
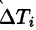
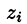
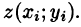

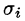
выражающую интеграл по поверхности S через двойной интеграл по проекции S на плоскость Оху.
Отметим, что если поверхность S задана уравнением вида у = y(x;z) или х = x(y;z), то аналогично получим:
где 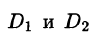
Пример:
Вычислить 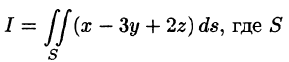
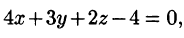
Решение:
Запишем уравнение плоскости в виде
Находим 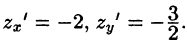
Пример:
где S — часть цилиндрической поверхности 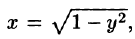
Решение:
Воспользуемся формулой (57.6). Поскольку
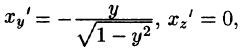
то где 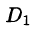
Некоторые приложения поверхностного интеграла I рода
Приведем некоторые примеры применения поверхностного интеграла I рода.
Площадь поверхности
Если поверхность S задана уравнением z = z(x; у), а ее проекция на плоскость Оху есть область D, в которой z(x;y), zx'(x; у) и zy'(x;y) — непрерывные функции, то ее площадь S вычисляется по формуле
Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы 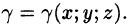
Масса поверхности
Пусть плотность распределения массы материальной поверхности есть 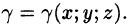
- Разбиваем поверхность S на п частей
площадь которой обозначим
.
- Берем произвольную точку
в каждой области
. Предполагаем, что в пределах области
плотность постоянна и равна значению ее в точке
.
- Масса
области
мало отличается от массы
фиктивной однородной области с постоянной плотностью
4. Суммируя 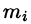
5.За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей 
Моменты, центр тяжести поверхности
Статистические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:
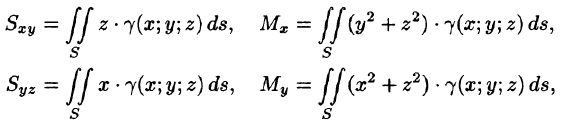
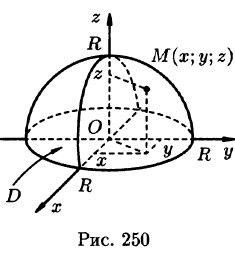
Пример:
Найти массу полусферы радиуса R, если в каждой точке поверхности плотность численно равна расстоянию этой точки от радиуса, перпендикулярного основанию полусферы. Решение: На рисунке 250 изображена полусфера радиуса R. Ее уравнение 
По формуле (57.7) находим:
Переходим к полярным координатам:
внутренний интеграл вычислен с помощью подстановки r= Rsint:
Видео:✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Поверхностный интеграл II рода
Поверхностный интеграл II рода строится по образцу криволинейного интеграла II рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет.
Пусть задана двусторонняя поверхность (таковой является плоскость, эллипсоид, любая поверхность, задаваемая уравнением z =f(x;y), где f(x;y), 
Далее, пусть в точках рассматриваемой двусторонней поверхности S в пространстве Oxyz определена непрерывная функция f(x; у; z). Выбранную сторону поверхности (в таком случае говорят, что поверхность ориентирована) разбиваем на части 
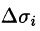
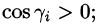
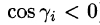
где 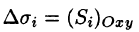

Предел интегральной суммы (58.1) при 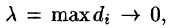

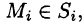
Аналогично определяются поверхностные интегралы II рода по переменным у и z и z и х:
Общим видом поверхностного интеграла II рода служит интеграл
где P, Q, R — непрерывные функции, определенные в точках двусторонней поверхности S.
Отметим, что если S — замкнутая поверхность, то поверхностный интеграл по внешней стороне ее обозначается 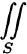
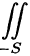
Из определения поверхностного интеграла II рода вытекают следующие его свойства:
- Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.
- Постоянный множитель можно выносить за знак поверхностного интеграла.
- Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
- Поверхностный интеграл II рода по всей поверхности
равен сумме интегралов по ее частям
(аддитивное свойство), если
пересекаются лишь по границе, их разделяющей.
- Если
— цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Вычисление поверхностного интеграла II рода
Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла.
Пусть функция R(x; у, z) непрерывна во всех точках поверхности S, заданной уравнением z = z(x; y), где z(x; у) — непрерывная функция в замкнутой области D (или 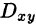
Выберем ту сторону поверхности S, где нормаль к ней образует с осью Oz острый угол. Тогда
Так как 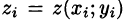
Правая часть этого равенства есть интегральная сумма для функции R(x;y;z(x;y)), непрерывной в области D. Переходя к пределу в равенстве (58.2) при 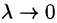
выражающую поверхностный интеграл II рода по переменным х и у через двойной интеграл. Если выбрать вторую сторону, т. е. нижнюю, поверхности S, то полученный двойной интеграл берут со знаком «минус». Поэтому
где 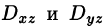
В формуле (58.5) поверхность S задана уравнением у = y(x;z), а в формуле (58.6) — уравнением х = x(y;z). Знаки перед интегралами выбираются в зависимости от ориентации поверхности S (так, в формуле (58.5) берем знак «плюс», если нормаль к поверхности образует с осью Оу острый угол, а знак «минус» — если тупой угол).
Для вычисления общего поверхностного интеграла II рода используют формулы (58.4)-(58.6), проектируя поверхность S на все три координатные плоскости:
Замечание:
Можно показать справедливость равенств
— элемент площади поверхности 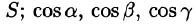
Поверхностные интегралы I и II рода связаны соотношением
Пример:
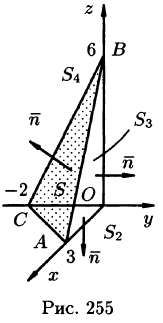
по верхней стороне части плоскости 2х — Зу + z = 6, лежащей в IV октанте.
Решение:
На рисунке 253 изображена заданная часть плоскости. Нормаль п, соответствующая указанной стороне поверхности, образует с осью Оу тупой угол, а с осями Ох и Oz — острые. В этом можно убедиться, найдя направляющие косинусы нормального вектора 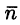
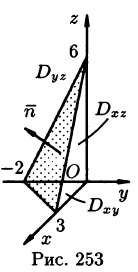
Поэтому перед двойными интегралами в формулах (58.4) и (58.6) следует брать знак «плюс», а в формуле (58.5) — знак «минус». Следовательно,
Формула Остроградского-Гаусса
Связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по объему, ограниченному этой поверхностью устанавливает следующая теорема.
Теорема:
Если функции P(x;y;z), Q(x;y,z), R(x;y;z) непрерывны вместе со своими частными производными первого порядка в пространственной области V, то имеет место формула
где S — граница области V и интегрирование по S производится по ее внешней стороне.
Формула (58.9) называется формулой Остроградского-Гаусса (является аналогом формулы Остроградского-Грина (см. п. 56.3).
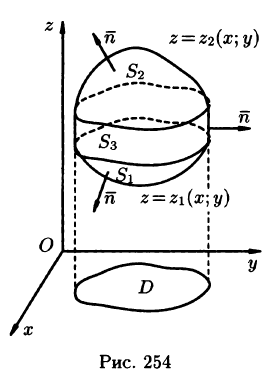
Пусть область V ограничена снизу поверхностью 
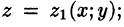
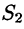
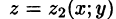
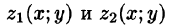
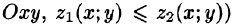
Рассмотрим тройной интеграл
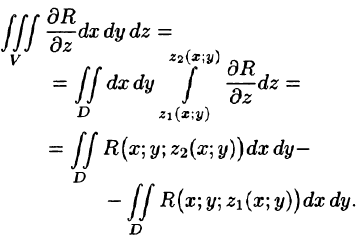
Двойные интегралы в правой части равенства заменим поверхностными интегралами II рода по внешней стороне поверхностей 
Добавляя равный нулю интеграл 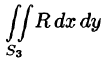
где S — поверхность, ограничивающая область V. Аналогично доказываются формулы
Складывая почленно равенства (58.10), (58.11) и (58.12), получаем формулу (58.9) Остроградского-Гаусса.
Замечания:
- Формула (58.9) остается справедливой для любой области V, которую можно разбить на конечное число областей рассмотренного вида.
- Формулу Остроградского-Гаусса можно использовать для вычисления поверхностных интегралов II рода по замкнутым поверхностям.
Пример:
где S — внешняя сторона пирамиды, ограниченной плоскостями 2х — Зу + z = 6, х = 0, у = 0, z = 0.
Решение:
По формуле (58.9) находим:
Заметим, что интеграл 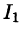
где поверхности 
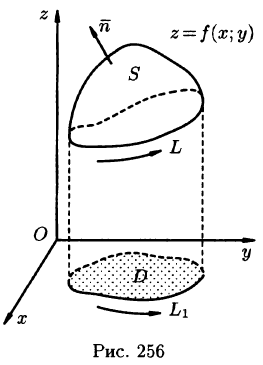
Формула Стокса
Связь между поверхностными и криволинейными интегралами II рода устанавливает следующая теорема.
Теорема:
Если функции P(x;y;z), Q(x;y;z) и R(x;y;z) непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности S, то имеет место формула
где L — граница поверхности S и интегрирование вдоль кривой L производится в положительном направлении (т. е. при обходе границы L поверхность S должна оставаться все время слева).
Формула (58.13) называется формулой Стокса (Д. Г. Стоке — английский математик, физик).
Пусть z = f(x;y) — уравнение поверхности S, функции 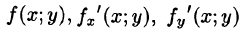
Будем считать, что поверхность S пересекается с любой прямой, параллельной оси Oz, не более чем в одной точке. Выберем верхнюю сторону поверхности S. Рассмотрим сначала интеграл вида
Значения функции Р(х; у; z) на L равны значениям функции P(x; y;z(x;y)) на 
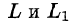
Применим к этому интегралу формулу Остроградского-Грина (см. п. 56.3). Тогда получим:
Преобразуем полученный двойной интеграл в равный ему поверхностный интеграл II рода (см. п. 58.2). Для этого последнее равенство перепишем в виде
(см. 58.7) и используем уравнение нормали к поверхности S (см. (45.3)). Так как выбрана верхняя сторона поверхности S, т. е. 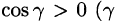
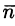
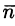
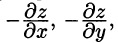
Отсюда 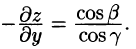
Аналогично получаются при соответствующих условиях еще два равенства:
Складывая почленно три последних равенства, получаем формулу Стокса (58.13).
Отметим, что формулу Стокса (58.13) можно применить и для поверхностей более сложного вида (разбив ее на части рассмотренного выше типа).
Формулу Стокса можно применять для вычисления криволинейного интеграла по замкнутому контуру с помощью поверхностного интеграла.
Из формулы Стокса вытекает, что если выполняются условия
то криволинейный интеграл по произвольному пространственному замкнутому контуру L равен нулю:
Следовательно, в данном случае криволинейный интеграл не зависит от вида пути интегрирования.
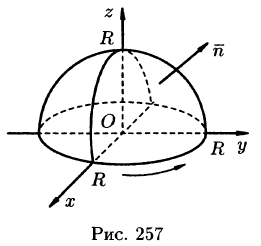
Пример:
Вычислить 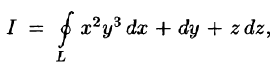
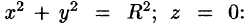
б) используя формулу Стокса, взяв в качестве поверхности полусферу
Решение: Поверхность интегрирования изображена на рисунке 257.
а) Запишем уравнение окружности в параметрической форме:
По формуле (56.7) имеем:
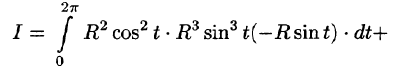
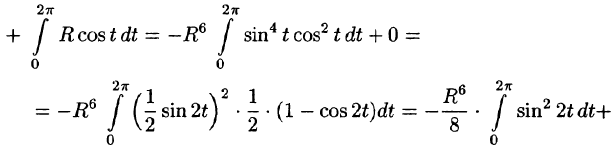
б) По формуле Стокса (58.13) находим:
Переходя к полярным координатам, получаем:
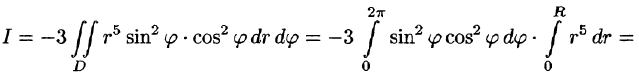
Некоторые приложения поверхностного интеграла II рода
С помощью поверхностного интеграла 11 рода можно найти объем тела, ограниченного сверху поверхностью 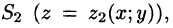
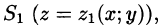
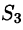
где
Действительно, положив в формуле Остроградского-Гаусса (58.9) 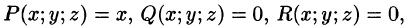
Аналогично, полагая P = 0, Q = у, R = 0, находим еще одну формулу для нахождения объема тела с помощью поверхностного интеграла II рода:
Наконец, положив Р = 0, Q = 0, R = z, по формуле (58.9) находим третью формулу
выражающую объем тела через поверхностный интеграл II рода.
Сложив почленно равенства (58.15)-(58.17) и разделив на три, получим формулу (58.14).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Криволинейный интеграл первого родаСкачать

Интеграл по окружности пример
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |













































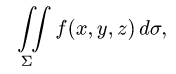
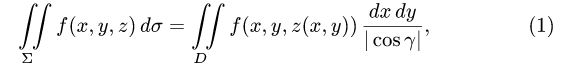
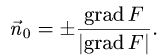
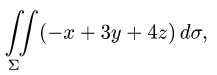
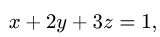
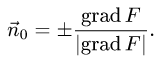
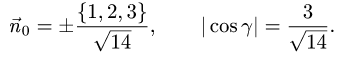
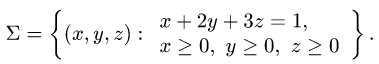
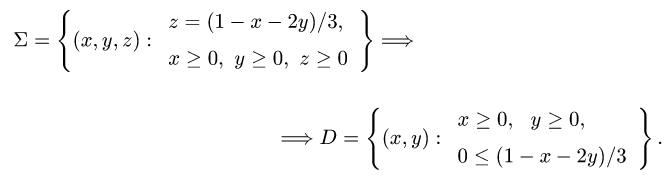
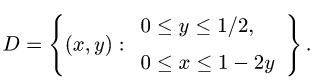
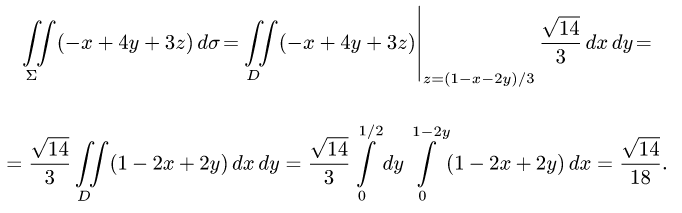
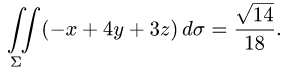
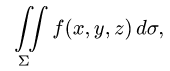
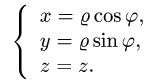
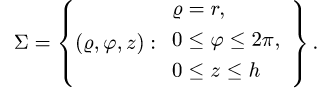
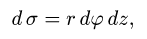
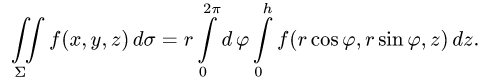
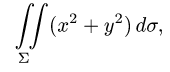
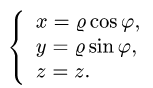
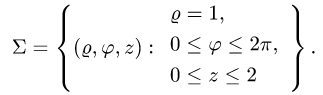
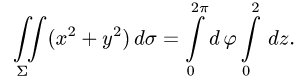
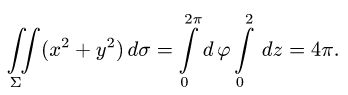
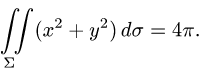
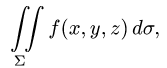
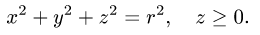
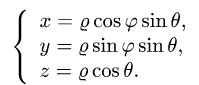
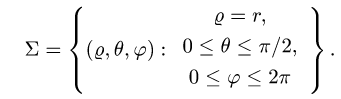
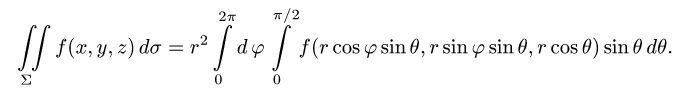
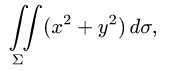
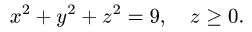
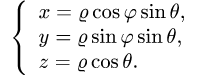
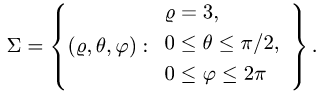
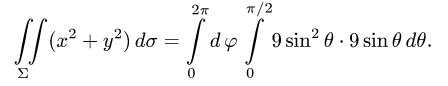
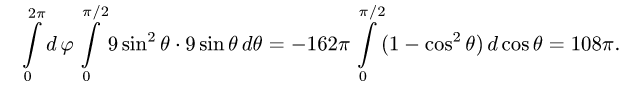
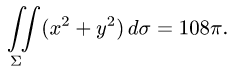


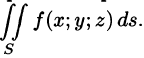
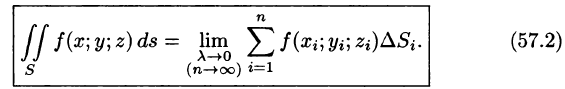
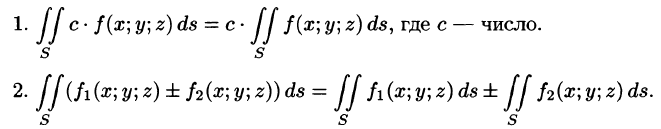
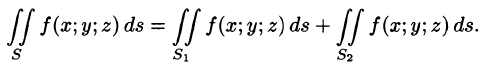
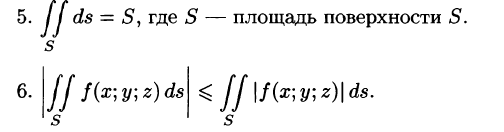
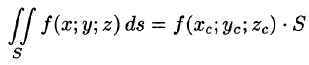
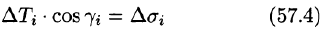
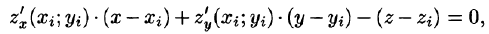
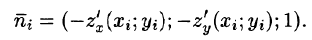
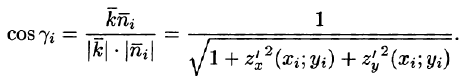
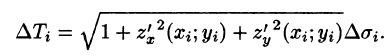
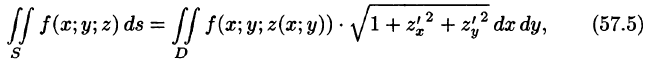
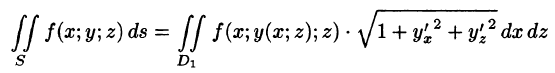
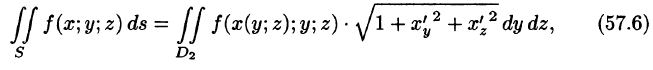
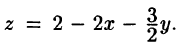
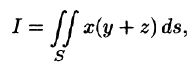
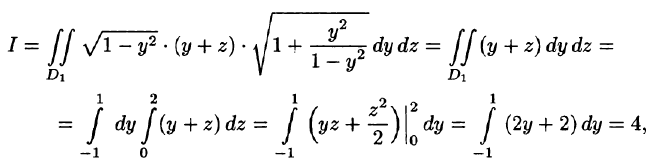
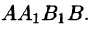
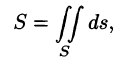
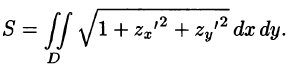
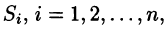 площадь которой обозначим
площадь которой обозначим 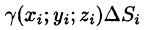 фиктивной однородной области с постоянной плотностью
фиктивной однородной области с постоянной плотностью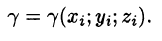
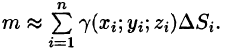
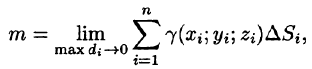
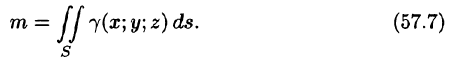
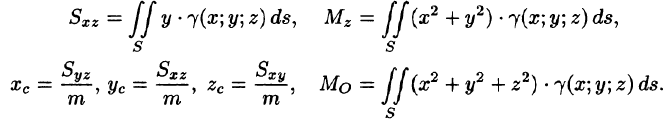
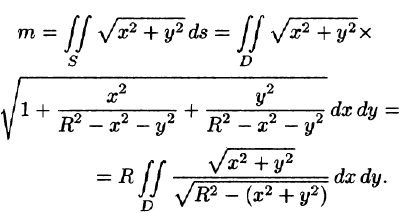
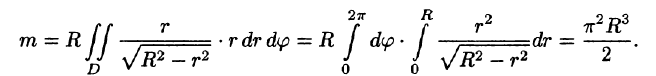
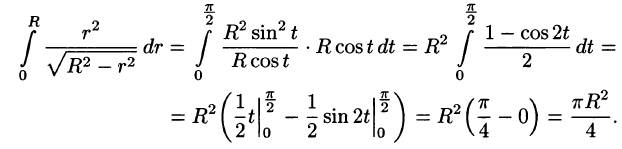

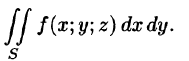
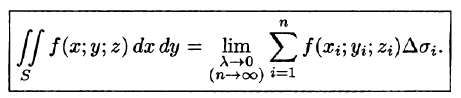
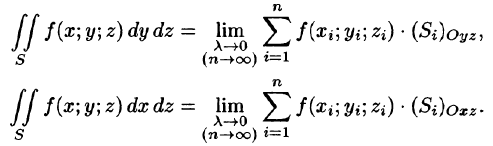
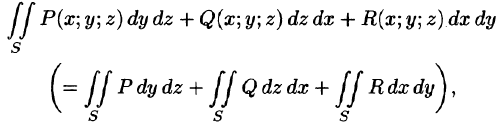
 равен сумме интегралов по ее частям
равен сумме интегралов по ее частям  — цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
— цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то