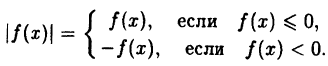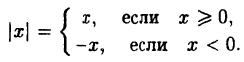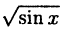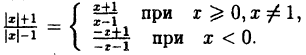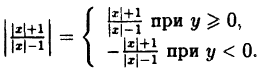В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее не постоянно хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по Х и по Y.
Сдвиг по горизонтали.
Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.
1. Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.
Теперь растяжение графика. Или сжатие.
2. Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в k раз по горизонтали, если , и сжат относительно исходного в k раз по горизонтали, если
3. Растяжение (сжатие) по вертикали
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в М раз по вертикали, если , и сжат относительно исходного в М раз по вертикали, если
И отражение по горизонтали.
4. Отражение по горизонтали
График функции симметричен графику функции относительно оси Y.
5. Отражение по вертикали.
График функции симметричен графику функции относительно оси Х.
Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.
6. Графики функций и
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.
Построим график функции
Конечно же, мы пользуемся определением модуля.
Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.
Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.
Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.
Вот самые простые задачи на преобразование графиков.
1. Построим график функции
Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.
Вершина в точке
2. Построим график функции
Выделим полный квадрат в формуле.
График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.
Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка
- Разрезание и разворачивание круговой диаграммы
- Полное разрезание круговой диаграммы
- Привлекайте внимание к небольшим срезам в круговой или линой круговой диаграмме
- Преобразования графиков функций с примерами решения и образцами выполнения
- Параллельный перенос графиков
- Сжатие и растяжение графиков
- Построение графиков с модулями
- Построение графиков функций с примерами
- 🎦 Видео
Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Разрезание и разворачивание круговой диаграммы
Чтобы выделить части круговой диаграммы, не изменяя при этом данные, можно вытащить отдельный сегмент,выделить всю круговую диаграмму или увеличить или сложить целые разделы с помощью круговой диаграммы или отрезка.
Чтобы подчеркнуть отдельный фрагмент круговой диаграммы, вы можете переместить его обратно от остальной части круговой диаграммы, вы графикив следующее:
Нажмите круговую диаграмму.
Дважды нажмите нужный сегмент и перетащите его от центра диаграммы.
Видео:Физика - движение по окружностиСкачать

Полное разрезание круговой диаграммы
Самый быстрый способ вытащить все срезы из круговой диаграммы — щелкнуть круговую диаграмму и перетащить ее от центра диаграммы.
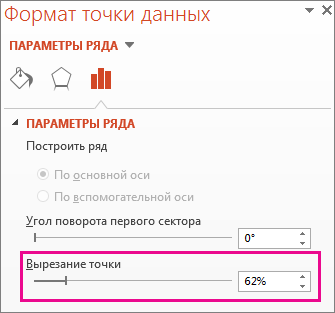
Чтобы более точно управлять расширением, выполните следующие действия:
Щелкните круговую диаграмму правой кнопкой мыши и выберите формат ряда данных.
Чтобы увеличить разделение, перетащите ползунок 2010 г. или введите число в поле в процентах.
Совет: Вы также можете поворачивать круговую диаграмму, поворачив ее.
Видео:Уравнение окружности (1)Скачать

Привлекайте внимание к небольшим срезам в круговой или линой круговой диаграмме
Круговая диаграмма и линеек круговой диаграммы упрощают просмотр небольших срезов круговой диаграммы. Эти типы диаграмм отделяют небольшие от основной круговой диаграммы и отображают их во вторичной круговой диаграмме или линеек с стопкой.
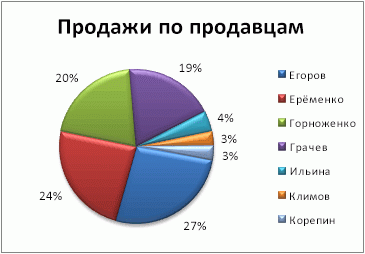
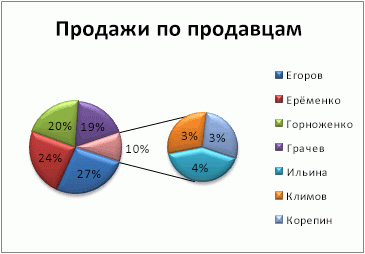
В приведенного ниже примере круговая диаграмма добавляет вторичную круговую диаграмму, чтобы отобразить три самых мелких фрагмента. Прежде чем сравнивать обычную круговую диаграмму:
с круговой диаграммой после:
Если не указать, сколько точек данных должно отображаться во вторичной круговой диаграмме или стопке, на диаграмме автоматически появятся три наименьших точки. В этом примере это 3%, 3% и 4%.
Выполните следующие действия, чтобы сделать это самостоятельно:
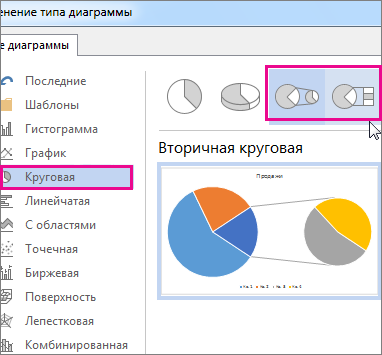
Щелкните диаграмму правой кнопкой мыши и выберите команду Изменить тип диаграммы для ряда.
Выберите пункт Круговая, а затем — Вторичная круговая или Вторичная линейчатая.
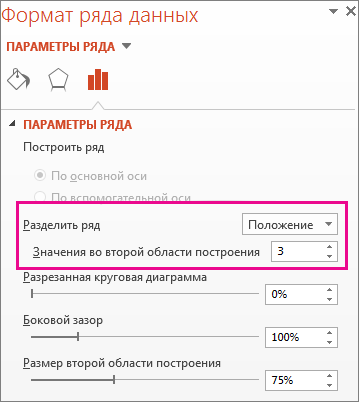
Чтобы изменить вид круговой диаграммы, щелкните ее часть, а затем в поле Разделить ряд на области Формат ряда данных выберите тип данных, которые будут отображаться на вторичной диаграмме.
Изменить количество точек данных вторичной диаграммы можно двумя способами.
Если ряд разделяется по позиции: в поле Значения во второй области уведите нужное количество позиций (например, 3, если вы хотите получить 3 наименьших).
Если ряд разделяется по значению или проценту: в поле Значения меньше введите другое число. В примере выше (с 3%, 3% и 4%) можно ввести 5 %.
Диаграмма слева — всегда основная, а диаграмма справа — всегда вторичная. Изменить их порядок нельзя.
Соединитеальные линии будут добавлены автоматически. Вы можете удалить их или изменить их стиль.
В Excel процентные значения в заголовках данных могут быть округлены. В этом случае, скорее всего, их не будет больше 100. Чтобы исправить эту ошибку, измените количество десятичных десятичных знаков, указанное в процентах, на вкладке Число в окне Формат ячеек (вкладка Главная > Группа Число, > диалоговое окно 
Видео:ДВИЖЕНИЕ ПО ОКРУЖНОСТИ 9 класс физика ПерышкинСкачать

Преобразования графиков функций с примерами решения и образцами выполнения
Параллельный перенос, сжатие и растяжение графиков. Построение графиков с модулями.
Графики многих функций можно получить из ранее рассмотренных с помощью элементарных геометрических преобразований: параллельного переноса, сжатия, растяжения, симметричного отображения. Рассмотрим некоторые из этих преобразований. Для каждого из элементарных преобразований предлагается два способа построения графика: с помощью преобразования графика и с помощью преобразования системы координат. Обучающийся должен выбрать тот, который кажется ему проще и овладеть им. В каждом случае считается известным график функции у = f(х).
Видео:Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать

Параллельный перенос графиков
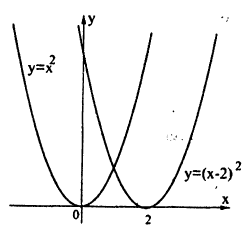
График функции у = /(x) + Ь получается из графика функции у = f(х) с помощью его переноса на вектор b = (0; b). Действительно, в этом случае ко всем ординатам графика у = f(х) прибавляется величина b, что означает сдвиг графика вдоль оси Оу. Если b > 0, то график функции у = f(х) переносится вверх параллельно оси Oy на b, если b 0 — вниз, если b 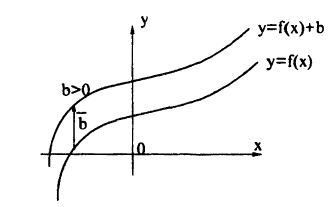
Пример:
График функции у = x² — 1 (рис. 50) смещен на 1 вниз параллельно оси Oy относительно графика функции у = х².
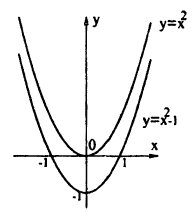
График функции у = f(x+a) получается с помощью переноса графика функции у = f(x) на вектор а = (—а;0). Действительно, перейдя к новым координатам X = х + α, Y = у параллельным переносом вдоль оси Ox на —а, заметим, что относительно новых координат получится исходный график функции Y = f(X). Если а > 0, то старые координаты получаются из новых сдвигом направо вдоль оси Ox на α, т.к. х = X — а. Если же сдвигать график, а не систему координат, то его нужно двигать в противоположном направлении — налево. Итак, если а > 0, то график функции у = f(x) переносится налево параллельно оси Ox на а, если а 0 — вправо, если α 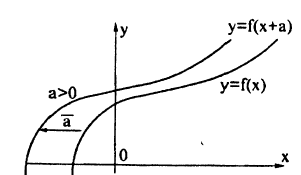
Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Сжатие и растяжение графиков
График функции у = kf(x), где к ∈ R, получается с помощью ’’растяжения” графика функции у = f(x) в к раз в направлении от оси Ох. ’’Растяжение” здесь понимается как умножение на к ординат всех точек графика у = f(x)∙ При k > 1 это будет действительно растяжение в к раз от оси Ox вдоль оси Оу. При 0 0 можно исправить значения по оси Оу, умножив их на k. При k 
При k > 1 график функции у = f(x) сжимается в k раз к оси Oy вдоль оси Ох; при 0 0 можно исправить значения по оси Ох, поделив их на k. При k 
Пользуясь изложенными методами, приведем последовательность преобразований при построении графика функции у = f(kx + b), если дан график функции у = f(x):
- нарисовать график функции у = f(x);
- получить график функции у = f(x + b), сдвинув исходный на вектор b = (-b; 0), как описано в п. 5.1;
- получить график функции у = f(kx + b), “сжав” предыдущий в к раз к оси Оу, как описано выше.
Пример:
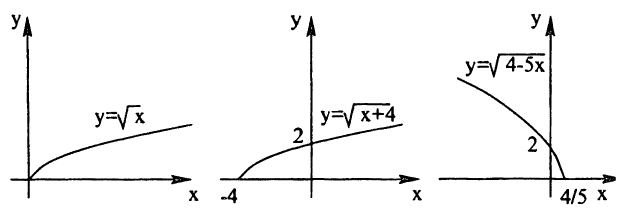
Написать последовательность преобразований и построить график функции у = 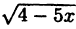
Решение:
- нарисуем график функции у = √х;
- о получим график функции у =
, сдвинув исходный на 4 единицы влево вдоль оси Ох;
- о получим график функции у =
, сжав предыдущий в 5 раз к оси Oy и затем отобразив симметрично относительно оси Оу.
Построение графика показано на рис. 55
Замечание:
Теперь понятно, что если функция у = f(x) периодическая с периодом Т, то функция у = К ∙ f(kx + b) + а тоже периодическая с периодом T₁ = 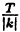
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Построение графиков с модулями
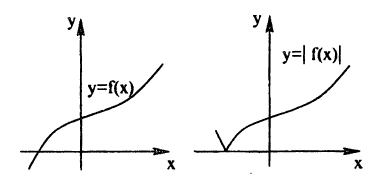
График функции у = ∣f(x)∣ получается из графика функции у = f(x) следующим образом (рис. 56)
- все части графика функции у = f(x), лежащие ниже оси Ох, следует отобразить вверх симметрично относительно этой оси;
- оставшиеся внизу части исходного графика следует стереть.
Действительно, по определению модуля действительного числа имеем:
(5.1)
Таким образом, те участки исходного графика, которые лежат не ниже оси Ox (f(x) ≥ 0), менять не нужно, а для тех участков, которые лежат ниже оси Ох, нужно построить функцию у = —f(x). В соответствии с п. 5.2 это получается симметричным отображением исходного графика относительно оси Ох. Заметим, что полученный график лежит не ниже оси Ох, что естественно, т.к. |f(x)| ≥ 0 для ∀x ∈ D(f).
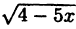
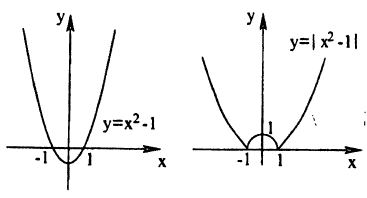
Пример:
Построение графика функции у = |х² — 1| показано на рис. 57.
График функции у = f (|x|) получается из графика функции у = f(х) следующим образом (рис. 58):
- все части графика функции у = f(x), лежащие слева от оси Оу, следует стереть;
- о оставшуюся часть графика следует отобразить налево симметрично относительно оси Оу.
Действительно, по определению модуля действительного числа имеем:
(5.2)
Таким образом, не нужно изменять те участки исходного графика, для которых х ≥ 0, а для х 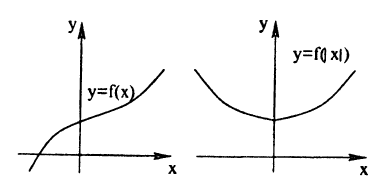
Пример:
Построение графика функции у = (|x| — 2)² показано на рис. 59
Элементарными методами можно строить эскизы графиков более сложных функций.
Пример:
Построить эскиз графика у =
Решение:
Построение графика показано на рис. 60. Заметим, что график отсутствует там, где sin х 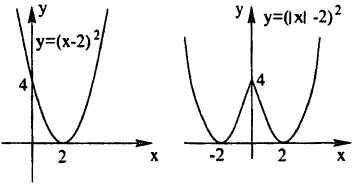
Кроме того, так как √u > и при 0 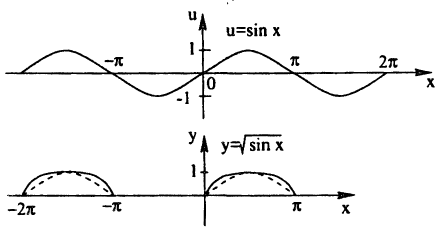
Видео:2 3 проекция точки на конусеСкачать

Построение графиков функций с примерами
Пример:
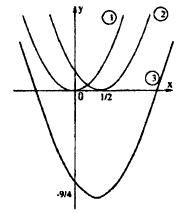
C помощью элементарных преобразований постройте график функции: у = x² — х — 2.
Решение:
Выделим полный квадрат из правой части уравнения функции: у = x² — х — 2 ⇔ y = x²-x+ 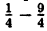
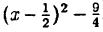
1) y =x²
2) у =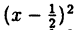
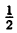
3) у = 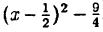
Пример:
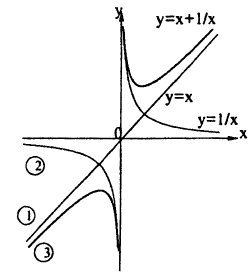
Используя сложение, деление функций, постройте график функции: у = х + 
Решение:
В одних осях координат нарисуем графики следующих функций (рис. 62):
1) у = х,
2) y=
3) y = x + 
Пример:
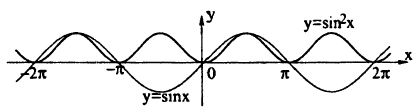
Постройте график сложной функции у = sin² х.
Решение:
В одних осях координат нарисуем графики функций:
1) y = sin x,
2) y = sin² х.
Учитывая, что квадрат числа меньшего единицы, меньше исходного числа, получим график (рис. 63)
Пример:
Постройте график функции в полярной системе координат: r = 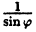
Решение:
Вычислим значения г для некоторых значений 
 | 0 | 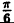 | 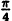 | 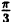 | 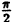 |
| r | ∞ | 2 | 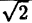 | 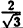 | ∞ |
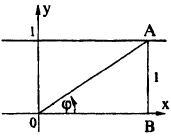
Соединив плавной линией найденные точки, получим линию вдоль оси Ох, проходящую через точку (0;1). Докажем что эта линия — прямая (рис. 64). Действительно: из Δ ОAВ ⇒ cos 
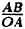
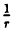
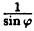
Пример:
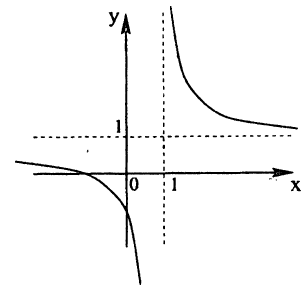
Постройте линию, описываемую уравнением, у =
Решение:
Сначала построим график функции у = 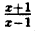
Наконец, строим линию описываемую уравнением у = 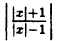
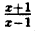
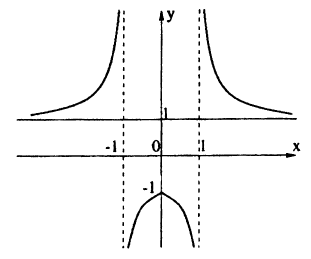
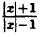
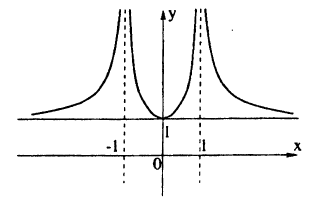
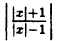
Пример:
Постройте линию, описываемую уравнением у =
Решение:
Для построения графика данного примера сначала постройте график функции у =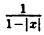
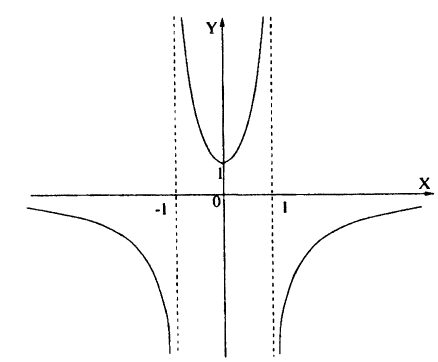
Пример:
Постройте линию, описываемую уравнением у = |х² — х -2|.
Решение:
Для построения графика данного примера сначала постройте график функции у = х² — х — 2. Затем отразите симметрично оси Ox ту часть графика, которая осталась снизу от оси Ох. Затем сотрите ту часть графика, которая расположена в нижней полуплоскости.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🎦 Видео
ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Тема: Путь и перемещениеСкачать

9 класс, 6 урок, Уравнение окружностиСкачать

Урок 89. Движение по окружности (ч.1)Скачать

УРАВНЕНИЕ ОКРУЖНОСТИ 8 и 9 класс геометрияСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать

Уравнение окружности. Как построить график уравнения окружности?Скачать

Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Уравнение окружностиСкачать

СФЕРА с вырезомСкачать













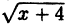 , сдвинув исходный на 4 единицы влево вдоль оси Ох;
, сдвинув исходный на 4 единицы влево вдоль оси Ох;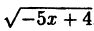 , сжав предыдущий в 5 раз к оси Oy и затем отобразив симметрично относительно оси Оу.
, сжав предыдущий в 5 раз к оси Oy и затем отобразив симметрично относительно оси Оу.