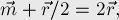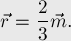Этот онлайн калькулятор находит центроид, или барицентр (центр тяжести) треугольника по координатам его вершин
Центр тяжести (центр масс, барицентр) треугольника для треугольника с равномерно распределённой массой (или в вершинах которого находятся равные массы) находится в центроиде треугольника. Центроидом называется точка пересечения медиан треугольника. Центроид относится к так называемым замечательным точкам треугольника. Например, помимо того, что он является центром тяжести, он также делит каждую медиану в отношении 2:1, считая от вершины, а три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника.
Чтобы вычислить положение центра тяжести по координатам вершин треугольника, достаточно вычислить среднее арифметическое координат вершин по оси x и по оси y, что и делает калькулятор ниже.
- Центры тяжести многоугольников и многогранников
- Двумерный случай: многоугольники
- Центр масс системы точек
- Центр масс каркаса
- Центр масс сплошной фигуры
- Случай треугольника
- Случай треугольника: доказательство
- Случай многоугольника
- Случай многоугольника: альтернативный способ
- Трёхмерный случай: многогранники
- Центр масс системы точек
- Центр масс каркаса многогранника
- Центр масс поверхности многогранника
- Центр масс сплошного многогранника
- Случай тетраэдра
- Случай произвольного многогранника
- Как определить центр масс треугольника
- 219. Четырехугольник.
- 220. Многоугольник.
- 221. Дуга окружности.
- 222. Круговой сектор.
- 223. Тетраэдр.
- 224. Пирамида с многоугольным основанием.
- 225. Призма. Цилиндр. Конус.
- 🌟 Видео
Видео:Центр тяжести треугольникаСкачать

Центры тяжести многоугольников и многогранников
Центром тяжести (или центром масс) некоторого тела называется точка, обладающая тем свойством, что если подвесить тело за эту точку, то оно будет сохранять свое положение.
Ниже рассмотрены двумерные и трёхмерные задачи, связанные с поиском различных центров масс — в основном с точки зрения вычислительной геометрии.
В рассмотренных ниже решениях можно выделить два основных факта. Первый — что центр масс системы материальных точек равен среднему их координат, взятых с коэффициентами, пропорциональными их массам. Второй факт — что если мы знаем центры масс двух непересекающихся фигур, то центр масс их объединения будет лежать на отрезке, соединяющем эти два центра, причём он будет делить его в то же отношении, как масса второй фигуры относится к массе первой.
Видео:координаты центра тяжести треугольникаСкачать

Двумерный случай: многоугольники
На самом деле, говоря о центре масс двумерной фигуры, можно иметь в виду одну из трёх следующих задач:
- Центр масс системы точек — т.е. вся масса сосредоточена только в вершинах многоугольника.
- Центр масс каркаса — т.е. масса многоугольника сосредоточена на его периметре.
- Центр масс сплошной фигуры — т.е. масса многоугольника распределена по всей его площади.
Каждая из этих задач имеет самостоятельное решение, и будет рассмотрена ниже отдельно.
Центр масс системы точек
Это самая простая из трёх задач, и её решение — известная физическая формула центра масс системы материальных точек:
где 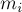
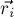
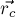
В частности, если все точки имеют одинаковую массу, то координаты центра масс есть среднее арифметическое координат точек. Для треугольника эта точка называется центроидом и совпадает с точкой пересечения медиан:
Для доказательства этих формул достаточно вспомнить, что равновесие достигается в такой точке 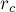
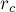
и, выражая отсюда 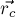
Центр масс каркаса
Будем считать для простоты, что каркас однороден, т.е. его плотность везде одна и та же.
Но тогда каждую сторону многоугольника можно заменить одной точкой — серединой этого отрезка (т.к. центр масс однородного отрезка есть середина этого отрезка), с массой, равной длине этого отрезка.
Теперь мы получили задачу о системе материальных точек, и применяя к ней решение из предыдущего пункта, мы находим:
где 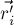

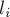

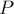
Для треугольника можно показать следующее утверждение: эта точка является точкой пересечения биссектрис треугольника, образованного серединами сторон исходного треугольника. (чтобы показать это, надо воспользоваться приведённой выше формулой, и затем заметить, что биссектрисы делят стороны получившегося треугольника в тех же соотношениях, что и центры масс этих сторон).
Центр масс сплошной фигуры
Мы считаем, что масса распределена по фигуре однородно, т.е. плотность в каждой точке фигуры равна одному и тому же числу.
Случай треугольника
Утверждается, что для треугольника ответом будет всё тот же центроид, т.е. точка, образованная средним арифметическим координат вершин:
Случай треугольника: доказательство
Приведём здесь элементарное доказательство, не использующее теорию интегралов.
Первым подобное, чисто геометрическое, доказательство привёл Архимед, но оно было весьма сложным, с большим числом геометрических построений. Приведённое здесь доказательство взято из статьи Apostol, Mnatsakanian «Finding Centroids the Easy Way».
Доказательство сводится к тому, чтобы показать, что центр масс треугольника лежит на одной из медиан; повторяя этот процесс ещё дважды, мы тем самым покажем, что центр масс лежит в точке пересечения медиан, которая и есть центроид.
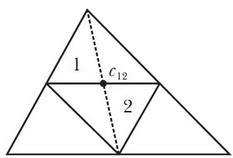
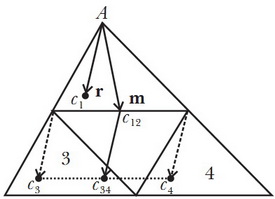
Разобьём данный треугольник 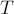
Четыре получившихся треугольника подобны треугольнику 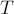
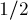
Треугольники №1 и №2 вместе образуют параллелограмм, центр масс которого 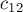
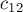
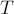
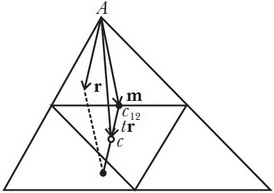
Пусть теперь вектор 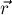
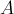
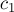
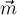
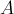
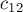
Наша цель — показать, что вектора 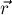
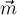
Обозначим через 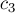
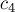

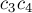
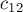

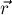
Искомый центр масс 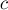
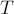
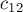

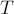
Таким образом, вектор от вершины 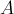
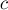
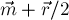
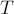
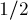
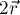
Таким образом, мы доказали, что вектора 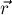
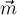
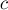
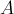
Более того, попутно мы доказали, что центроид делит каждую медиану в отношении 
Случай многоугольника
Перейдём теперь к общему случаю — т.е. к случаю мноугоугольника. Для него такие рассуждения уже неприменимы, поэтому сведём задачу к треугольной: а именно, разобьём многоугольник на треугольники (т.е. триангулируем его), найдём центр масс каждого треугольника, а затем найдём центр масс получившихся центров масс треугольников.
Окончательная формула получается следующей:
где 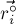

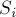

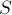
Триангуляция выпуклого многоугольника — тривиальная задача: для этого, например, можно взять треугольники 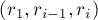
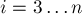
Случай многоугольника: альтернативный способ
С другой стороны, применение приведённой формулы не очень удобно для невыпуклых многоугольников, поскольку произвести их триангуляцию — сама по себе непростая задача. Но для таких многоугольников можно придумать более простой подход. А именно, проведём аналогию с тем, как можно искать площадь произвольного многоугольника: выбирается произвольная точка 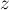
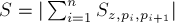
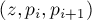
где 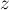
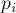
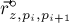
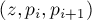
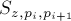
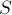

Видео:Урок 79. Центр масс тела и методы определения его положенияСкачать

Трёхмерный случай: многогранники
Аналогично двумерному случаю, в 3D можно говорить сразу о четырёх возможных постановках задачи:
- Центр масс системы точек — вершин многогранника.
- Центр масс каркаса — рёбер многогранника.
- Центр масс поверхности — т.е. масса распределена по площади поверхности многогранника.
- Центр масс сплошного многогранника — т.е. масса распределена по всему многограннику.
Центр масс системы точек
Как и в двумерном случае, мы можем применить физическую формулу и получить тот же самый результат:
который в случае равных масс превращается в среднее арифметическое координат всех точек.
Центр масс каркаса многогранника
Аналогично двумерному случаю, мы просто заменяем каждое ребро многогранника материальной точкой, расположенной посередине этого ребра, и с массой, равной длине этого ребра. Получив задачу о материальных точках, мы легко находим её решение как взвешенную сумму координат этих точек.
Центр масс поверхности многогранника
Каждая грань поверхности многогранника — двухмерная фигура, центр масс которой мы умеем искать. Найдя эти центры масс и заменив каждую грань её центром масс, мы получим задачу с материальными точками, которую уже легко решить.
Центр масс сплошного многогранника
Случай тетраэдра
Как и в двумерном случае, решим сначала простейшую задачу — задачу для тетраэдра.
Утверждается, что центр масс тетраэдра совпадает с точкой пересечения его медиан (медианой тетраэдра называется отрезок, проведённый из его вершины в центр масс противоположной грани; таким образом, медиана тетраэдра проходит через вершину и через точку пересечения медиан треугольной грани).
Почему это так? Здесь верны рассуждения, аналогичные двумерному случаю: если мы рассечём тетраэдр на два тетраэдра с помощью плоскости, проходящей через вершину тетраэдра и какую-нибудь медиану противоположной грани, то оба получившихся тетраэдра будут иметь одинаковый объём (т.к. треугольная грань разобьётся медианой на два треугольника равной площади, а высота двух тетраэдров не изменится). Повторяя эти рассуждения несколько раз, получаем, что центр масс лежит на точке пересечения медиан тетраэдра.
Эта точка — точка пересечения медиан тетраэдра — называется его центроидом. Можно показать, что она на самом деле имеет координаты, равные среднему арифметическому координат вершин тетраэдра:
(это можно вывести из того факта, что центроид делит медианы в отношении 
Таким образом, между случаями тетраэдра и треугольника принципиальной разницы нет: точка, равная среднему арифметическому вершин, является центром масс сразу в двух постановках задачи: и когда массы находится только в вершинах, и когда массы распределены по всей площади/объёму. На самом деле, этот результат обобщается на произвольную размерность: центр масс произвольного симплекса (simplex) есть среднее арифметическое координат его вершин.
Случай произвольного многогранника
Перейдём теперь к общему случаю — случаю произвольного многогранника.
Снова, как и в двумерном случае, мы производим сведение этой задачи к уже решённой: разбиваем многогранник на тетраэдры (т.е. производим его тетраэдризацию), находим центр масс каждого из них, и получаем окончательный ответ на задачу в виде взвешенной суммы найденных центров масс.
Видео:Центр тяжести. ЭкспериментСкачать

Как определить центр масс треугольника
Медиана треугольника есть диаметр, делящий пополам хорды, параллельные основанию, поэтому на ней лежит центр тяжести (п° 217) площади треугольника. Следовательно, три медианы треугольника, пересекаясь, определяют центр тяжести площади треугольника.
Элементарные соображения показывают, что медианы треугольника пересекаются в точке, отстоящей на две трети длины каждой из них от соответствующей вершины. Поэтому центр тяжести площади треугольника лежит на любой его медиане на расстоянии двух третей ее длины от вершины.
219. Четырехугольник.
Центр тяжести площади четырехугольника определяется пересечением двух прямых, которые мы получаем, применяя распределительное свойство центров тяжести (п° 213).
Сначала делим четырехугольник диагональю на два треугольника. Центр тяжести четырехугольника лежит на прямой, соединяющей центры тяжести этих треугольников. Эта прямая и есть первая из двух искомых прямых.
Вторую прямую получим таким же способом, разбивая четырехугольник на два треугольника (отличных от предыдущих) посредством другой диагонали.
220. Многоугольник.
Мы знаем способы нахождения центров тяжести площади треугольника и четырехугольника. Чтобы определить центр тяжести площади многоугольника с произвольным числом сторон, предположим, что мы умеем находить центр тяжести площади многоугольника с меньшим числом сторон.
Тогда можно поступить так же, как в случае четырехугольника. Площадь данного многоугольника делят на две части двумя разными способами проведением диагоналей. В каждом из двух случаев соединяют прямой центры тяжести отдельных частей. Эти две прямые пересекаются в искомом центре тяжести.
221. Дуга окружности.
Пусть требуется определить центр тяжести дуги окружности АВ длины s. Отнесем окружность к двум взаимно перпендикулярным диаметрам ОХ и OY, из которых первый проходит через середину С дуги АВ. Центр тяжести лежит на оси ОХ, являющейся осью симметрии. Достаточно поэтому определить 5. Для этого имеем формулу:
Пусть будут: а — радиус окружности, с — длина хорды АВ, 


Тогда, принимая В за переменную интегрирования и выполняя интегрирование вдоль дуги АВ, получим:
Следовательно, центр тяжести дуги окружности лежит на радиусе, проведенном через середину дуги, в точке, расстояние которой от центра окружности есть четвертая пропорциональная длины дуги, радиуса и хорды.
222. Круговой сектор.
Сектор, заключенный между дугой окружности и двумя радиусами ОА и ОВ, может быть разложен промежуточными радиусами на бесконечно малые равные между собою секторы. Эти элементарные секторы можно рассматривать как бесконечно узкие треугольники; центр тяжести каждого из них, по предыдущему, лежит на радиусе, проведенном через середину элементарной дуги этого сектора, на расстоянии двух третей длины радиуса от центра окружности. Равные между собою массы всех элементарных треугольников, сосредоточенные в их центрах тяжести, образуют однородную дугу окружности, радиус которой равен двум третям радиуса дуги сектора. Рассматриваемый случая приводится, таким образом, к отысканию центра тяжести этой однородной дуги, т. е. к задаче, решенной в предыдущем п°.
223. Тетраэдр.
Определим центр тяжести объема тетраэдра. Плоскость, проходящая через одно из ребер и через середину противоположного ребра, есть диаметральная плоскость, которая делит пополам хорды, параллельные этому последнему ребру: она содержит поэтому центр тяжести объема тетраэдра. Следовательно, шесть плоскостей, тетраэдра, из которых каждая проходит через одно из ребер и через середину противоположного ребра, пересекаются в одной точке, представляющей собой центр тяжести объема тетраэдра.
Рассмотрим тетраэдр ABCD (фиг. 37); соединим вершину А с центром тяжести I основания BCD; прямая AI есть пересечение диаметральных плоскостей, проходящих
через ребра АВ и 






Следовательно, центр тяжести объема тетраэдра лежит на отрезке, соединяющем любую вершину тетраэдра с центром тяжести противоположной грани, на расстоянии трех четвертей длины этого отрезка от вершины.
Заметим еще, что прямая, соединяющая середины Я и L двух противоположных ребер (фиг. 38) есть пересечение диаметральных плоскостей, проходящих через эти ребра, она также проходит через центр тяжести тетраэдра. Таким образом, три прямые, соединяющие середины противоположных ребер тетраэдра, пересекаются в его центре тяжести.
Пусть Н и 
двум ребрам. Прямые HL и MN, соединяющие середины двух противоположных ребер, суть диагонали этого параллелограма, а значит, они в точке пересечения делятся пополам. Таким образом, центр тяжести тетраэдра лежит в середине отрезка, соединяющего середины двух противоположных ребер тетраэдра.
224. Пирамида с многоугольным основанием.
Центр тяжести пирамиды лежит на отрезке, соединяющем вершину пирамиды с центром тяжести основания на расстоянии трех четвертей длины этого отрезка от вершины.
Чтобы доказать эту теорему, разложим пирамиду на тетраэдры плоскостями, проведенными через вершину пирамиды и через диагонали основания ABCD 
Проведем плоскость 

225. Призма. Цилиндр. Конус.
На основании симметрии, центры тяжести призмы и цилиндра лежат на середине отрезка, соединяющего центры тяжести оснований.
Рассматривая конус, как предел вписанной в него пирамиды с той же вершиной, убеждаемся, что центр тяжести конуса лежит на отрезке, соединяющем вершину конуса с центром тяжести основания, на расстоянии трех четвертей длины этого отрезка от вершины. Можно также сказать, что центр тяжести конуса совпадает с центром тяжести сечения конуса плоскостью, параллельной основанию и проведенной на расстоянии одной четверти высоты конуса от основания.
🌟 Видео
Видеоурок 3. Определение центра тяжести.Скачать

Определение центра тяжести сложной фигуры. СопроматСкачать

Найдите центр тяжестиСкачать

Механика | динамика | центр масс треугольникаСкачать

Урок 80. Определение положения центра масс телаСкачать

Центры тяжести прямоугольных треугольниковСкачать
Центр тяжестиСкачать

Практическая №5 Определение центра тяжести сложной фигурыСкачать

97 Медианы и центр тяжести треугольникаСкачать

Центр массСкачать

Центр масс в математике (или механика помогает геометрии)Скачать

Определение центра тяжести сложных сечений. Фигуры из ГОСТ.Скачать

Как найти центр тяжести любой фигуры?Скачать

Определение центра тяжести плоской фигуры. Подробное объяснение. Сопромат для чайниковСкачать

3.3. Центр масс и закон его движения | Динамика | Александр Чирцов | ЛекториумСкачать

Центр тяжести фигуры неправильной формы.Скачать