Как определить положение точек относительно окружности (4 видео)

Взаимное расположение точки и окружности

Содержание

Существует 3 варианта взаимного расположения точки и окружности:
Как отличить друг от друга эти варианты?
А как найти расстояние между двумя точками?
Формула
Если лень читать
Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2
Вступление
Как найти координаты точки?
Понятие системы координат
Определение координат точки
Особые случаи расположения точек
Способы нахождения точки по её координатам
💥 Видео

Видео:Как искать точки на тригонометрической окружности.Скачать

Существует 3 варианта взаимного расположения точки и окружности:

Точка находится внутри круга, ограниченного окружностью:

Точка находится на окружности:

Точка находится вне круга, ограниченного окружностью:

Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Как отличить друг от друга эти варианты?

Вспомним определения окружности и круга:

Окружность — геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние, называемое её радиусом.
Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга.

Из определений следует, что точка принадлежит окружности тогда и только тогда, когда расстояние между ней и центром равно радиусу, открытому кругу (так называют круг, в который не входит его граница) — когда расстояние меньше радиуса, лежит вне круга — когда расстояние больше радиуса. Картинка ниже подтвеждает это.

Итак, определение положения точки относительно окружности сводится к вычислению расстояния между двумя точками (данной точкой и центром окружности) и сравнению этой величины с радиусом.

Видео:Задача на положение точки относительно окружности(видео 55) | Подобие. Геометрия | МатематикаСкачать

А как найти расстояние между двумя точками?

Точно так же, как длину отрезка или вектора с началом в одной из этих точек и концом в другой, — через теорему Пифагора.

Пусть координаты первой точки, А — (x_1) и (y_1), а второй, B — (x_2) и (y_2):

Построим прямоугольный треугольник с катетами, параллельными осям координат, и гипотенузой AB:

Катет OB в нём равен (x_2-x_1), катет OA — (y_1-y_2), значит, гипотенуза AB – корню из их суммы, т. е. [sqrt] Приведённая выше формула подходит для любых координат точек. Часто значения в скобках получаются отрицательными, в том числе и для катета OA в примере, но при возведении в квадрат знак теряется.

Ещё одна оговорка: при извлечении квадратного корня получается приближённое значение, которое может отличаться от привычного нам. Поэтому, если нам требуется сравнить расстояние с каким-то числом (что мы и собираемся сделать), удобнее не извлекать корень и сравнивать квадрат расстояния с квадратом числа.

Кстати, если вектор задан одной точкой, его длину можно определить по той же формуле, но чуть проще.

В самом деле, здесь (x_1=y_1=0), поэтому формула выглядит как [sqrt] Также ей можно пользоваться, когда одна из точек или один из концов отрезка находится в точке (0;0). Разумеется, здесь тоже действуют оговорки, описанные выше.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Формула

Теперь нетрудно вывести формулу, по которой можно определить взаимное расположение точки и окружности.

Если (px) и (py) — координаты точки, (ox) и (oy) — координаты центра окружности, (r) — радиус окружности, то

при ((ox-px)^2+(oy-py)^2lt) точка лежит внутри круга;

при ((ox-px)^2+(oy-py)^2=) точка лежит на окружности;

при ((ox-px)^2+(oy-py)^2gt) точка лежит вне круга.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Если лень читать

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP₁P₂ – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P₁M, P₁P₂) 2 .

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Как найти координаты точки?

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:Точка встречи прямой с плоскостьюСкачать

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

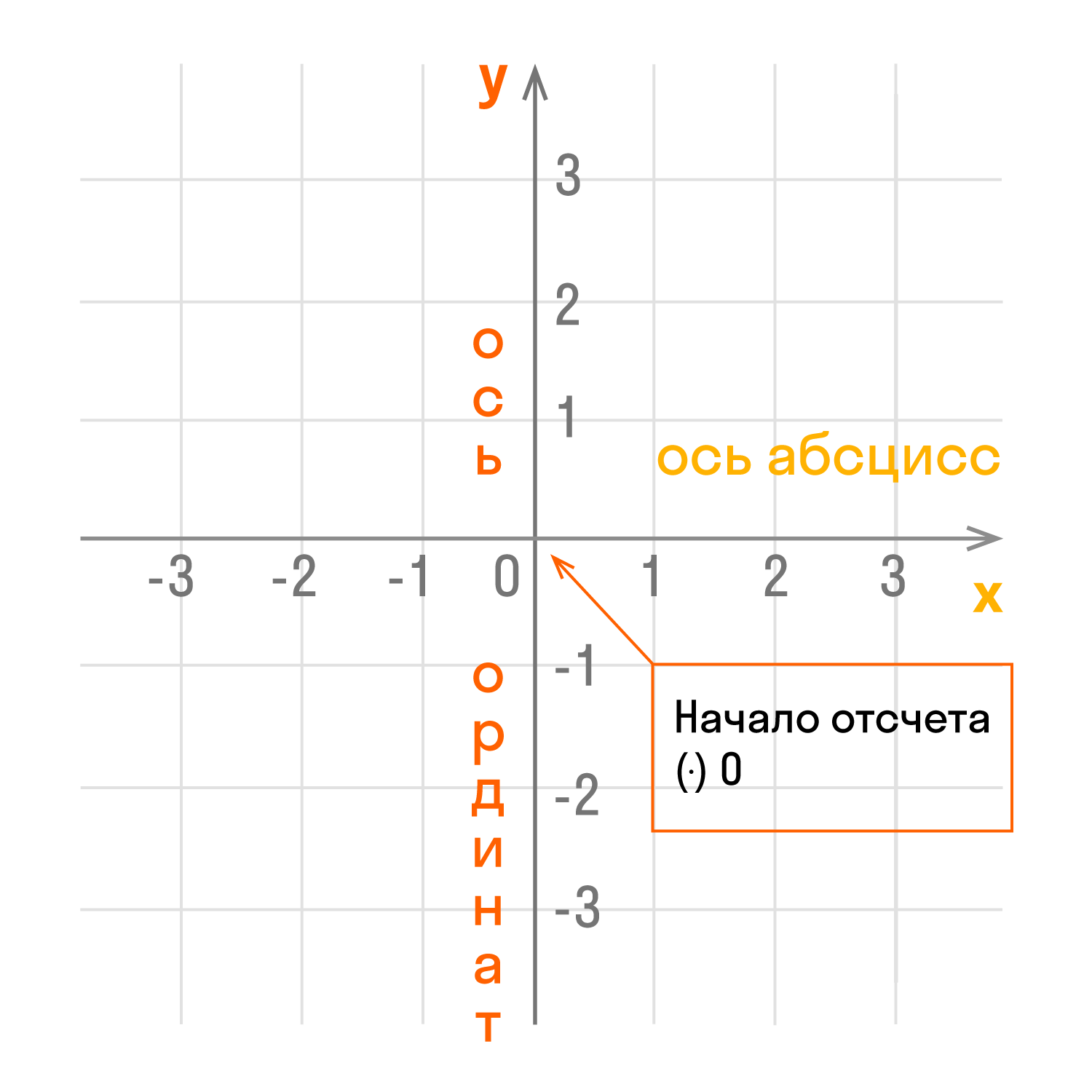
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Координатные оси — это прямые, образующие систему координат.
Ось абсцисс Ox — горизонтальная ось.
Ось ординат Oy — вертикальная ось.
Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

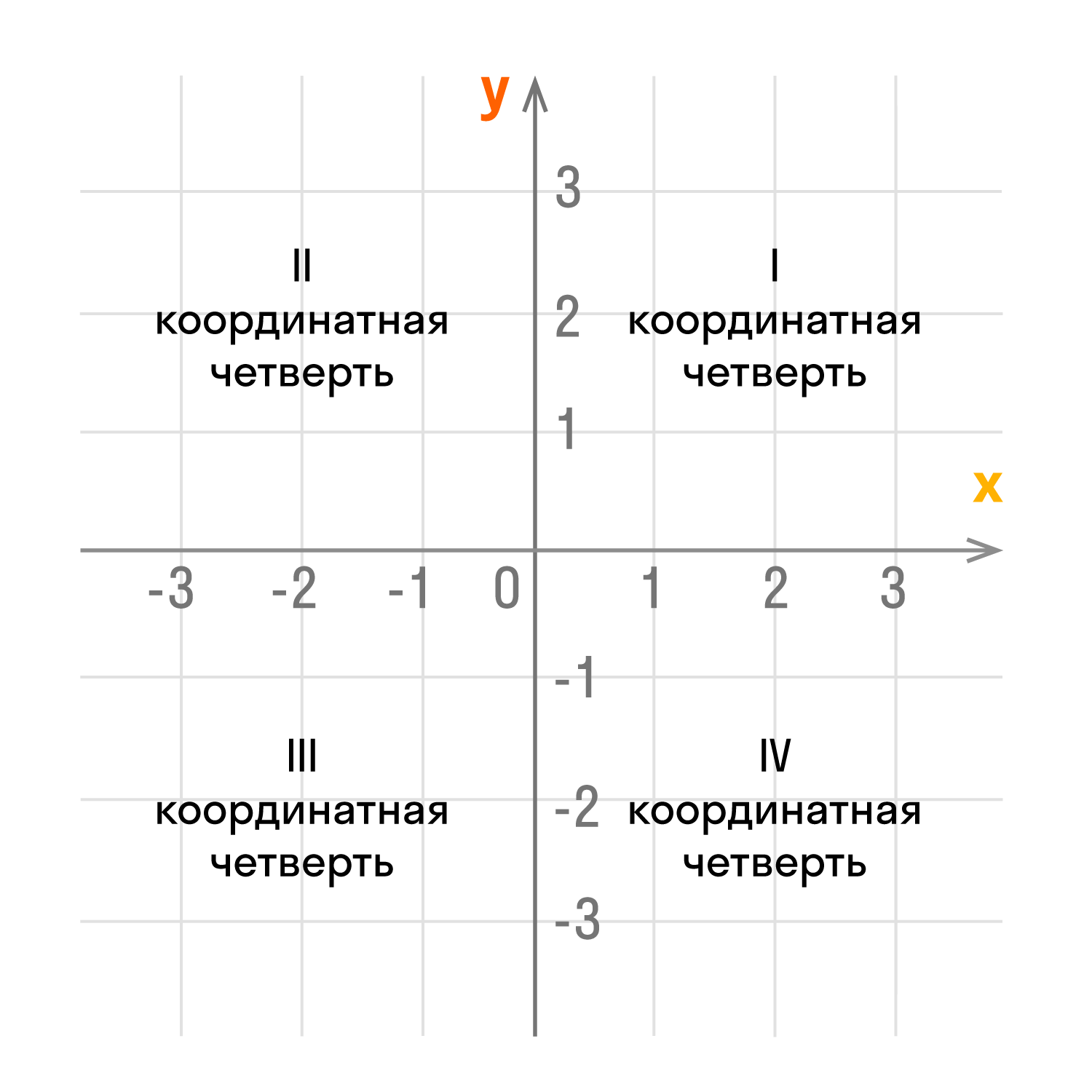
Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

верхний правый угол — первая четверть I;
верхний левый угол — вторая четверть II;
нижний левый угол — третья четверть III;
нижний правый угол — четвертая четверть IV;

Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
Если обе координаты отрицательны, то число находится в третьей четверти.
Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

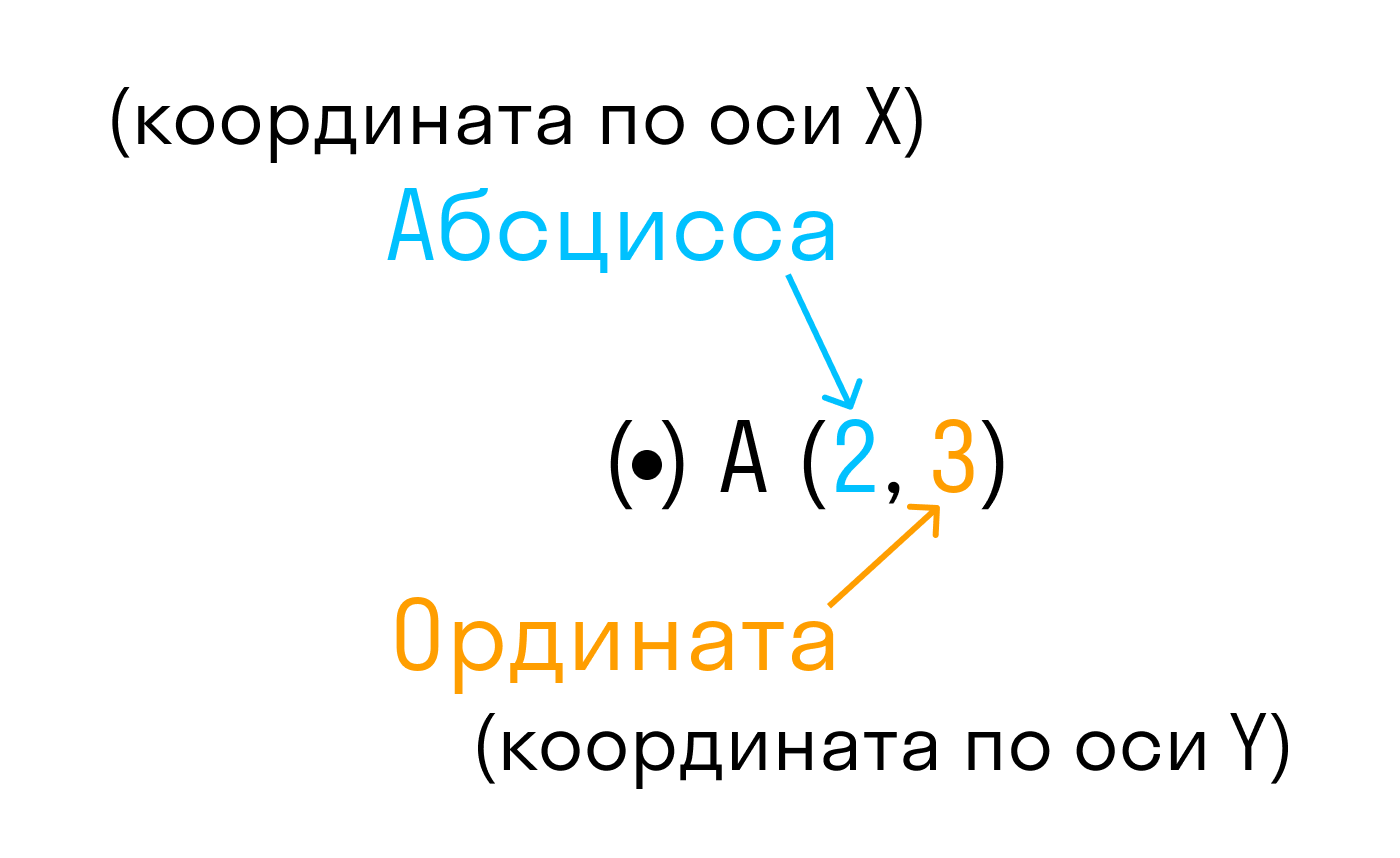
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

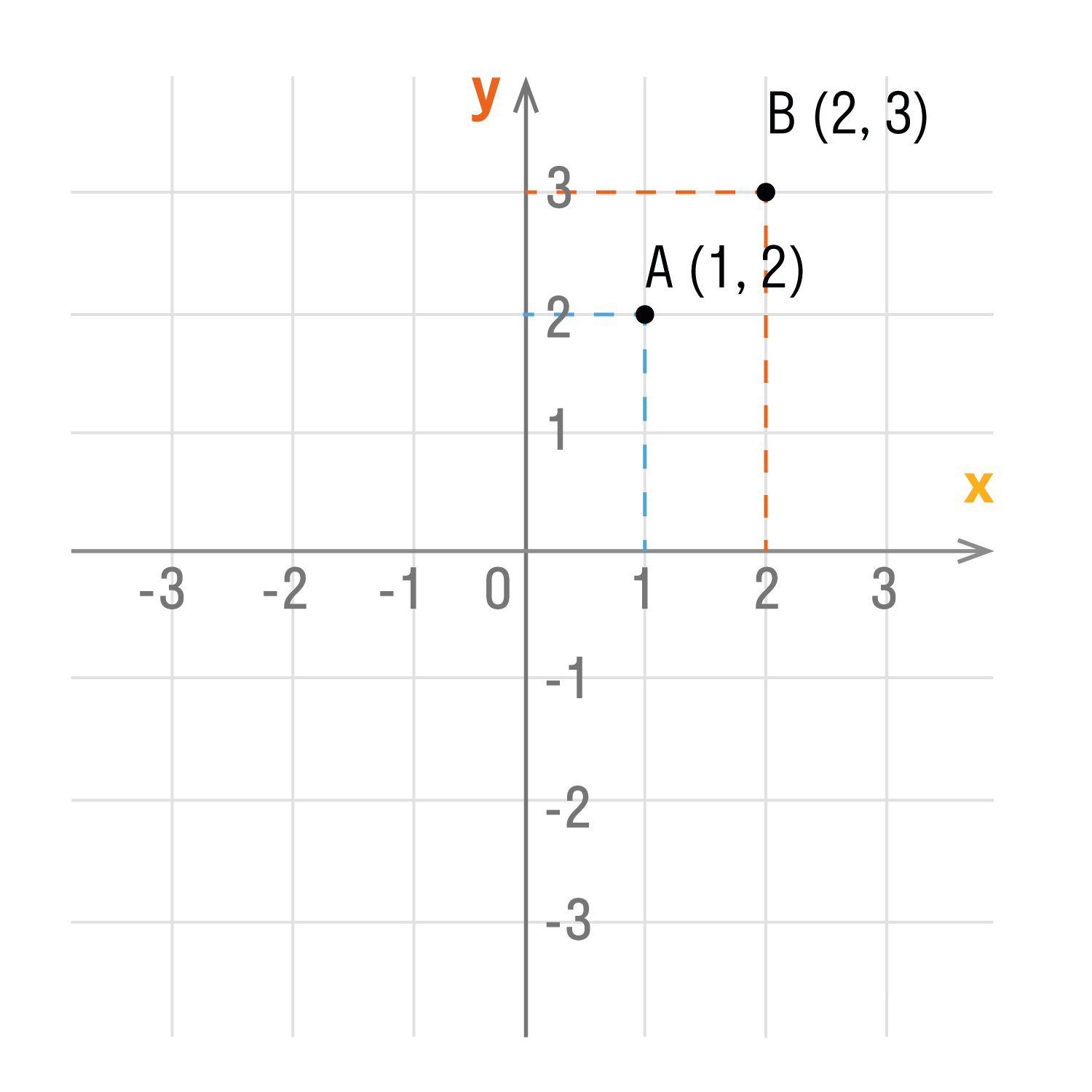
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Видео:✓ Степень точки в ЕГЭ | Резерв досрока ЕГЭ-2022. Задание 16. Профильный уровень | Борис ТрушинСкачать

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

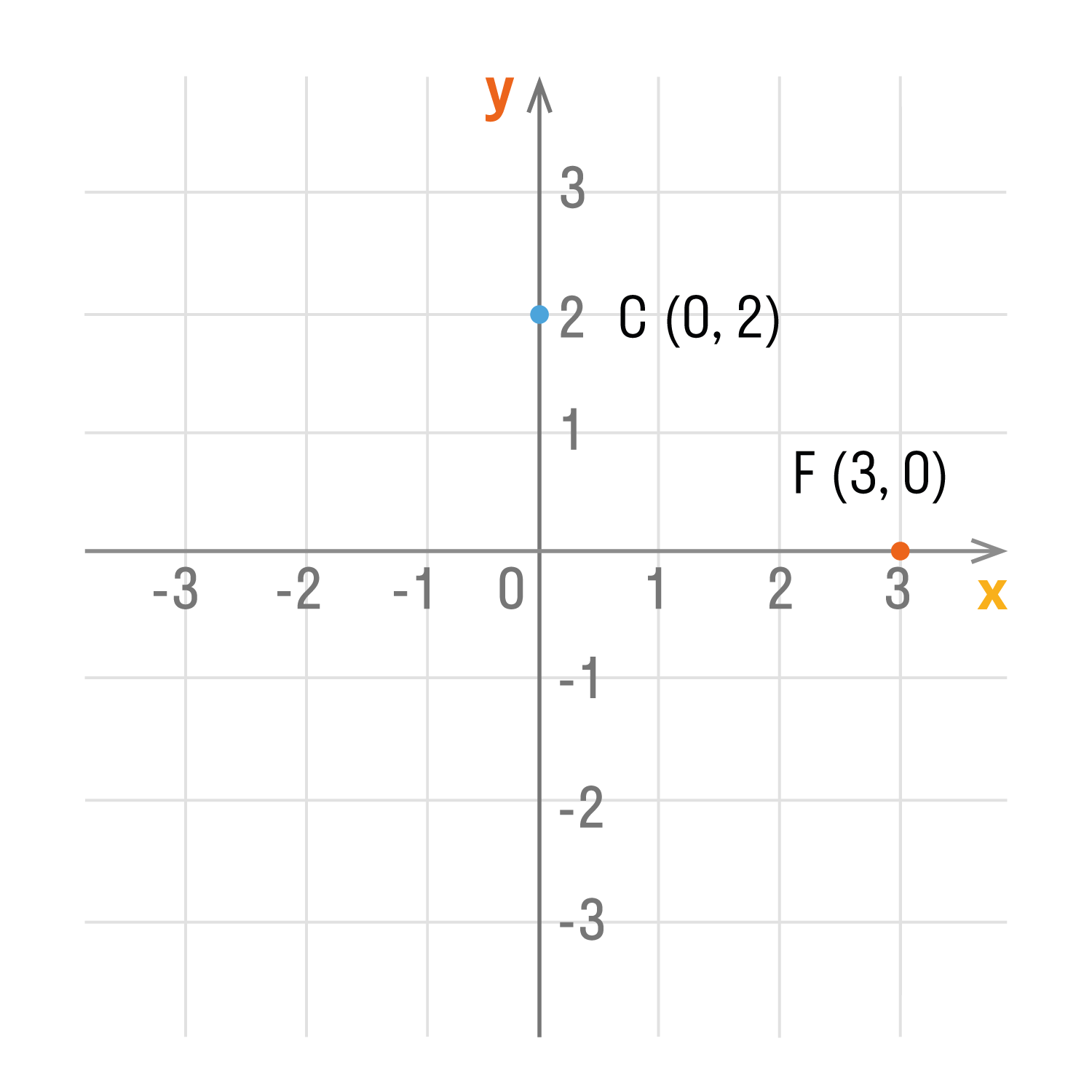
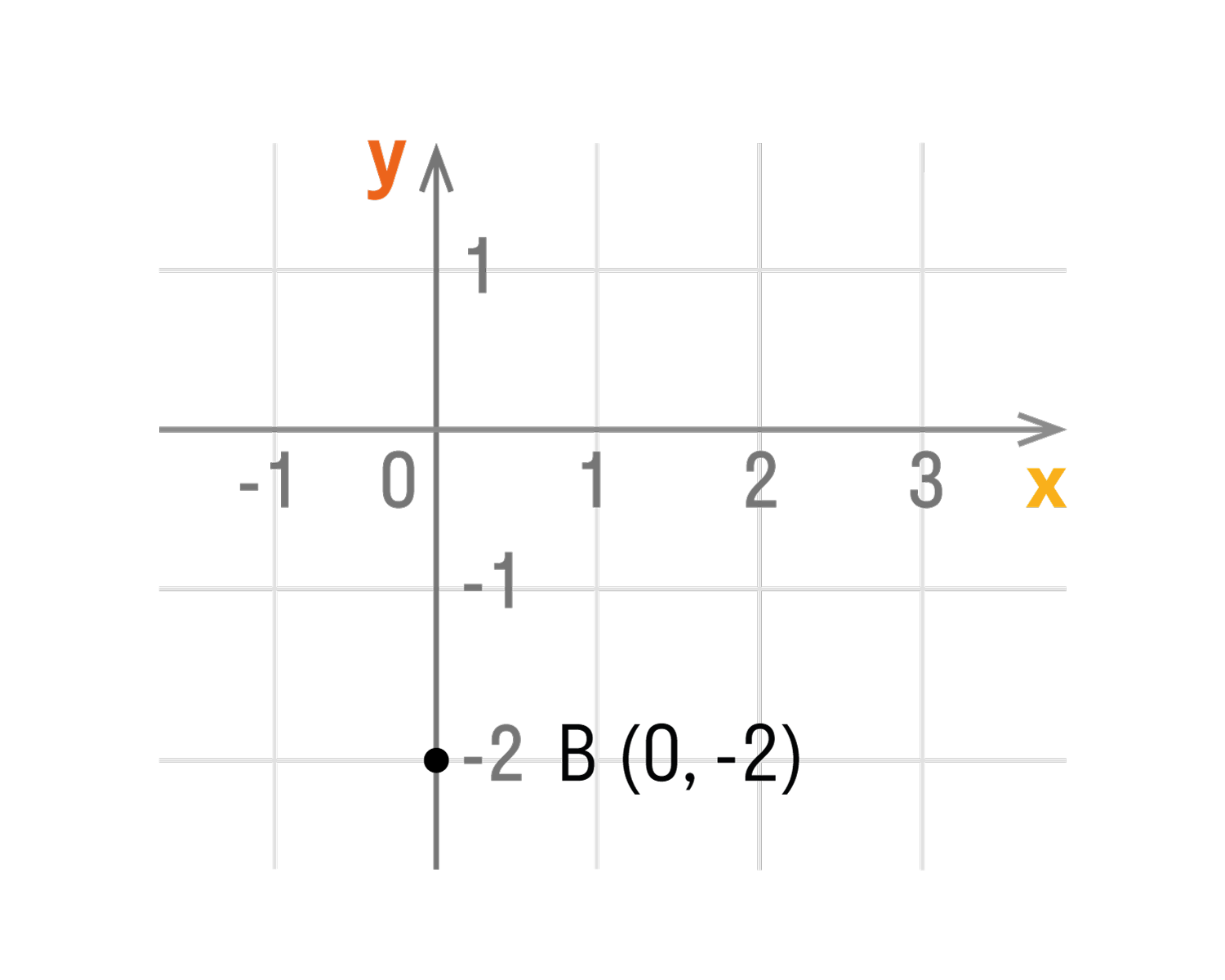
Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2).
Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0).
Начало координат — точка O. Ее координаты равны нулю: O (0,0).
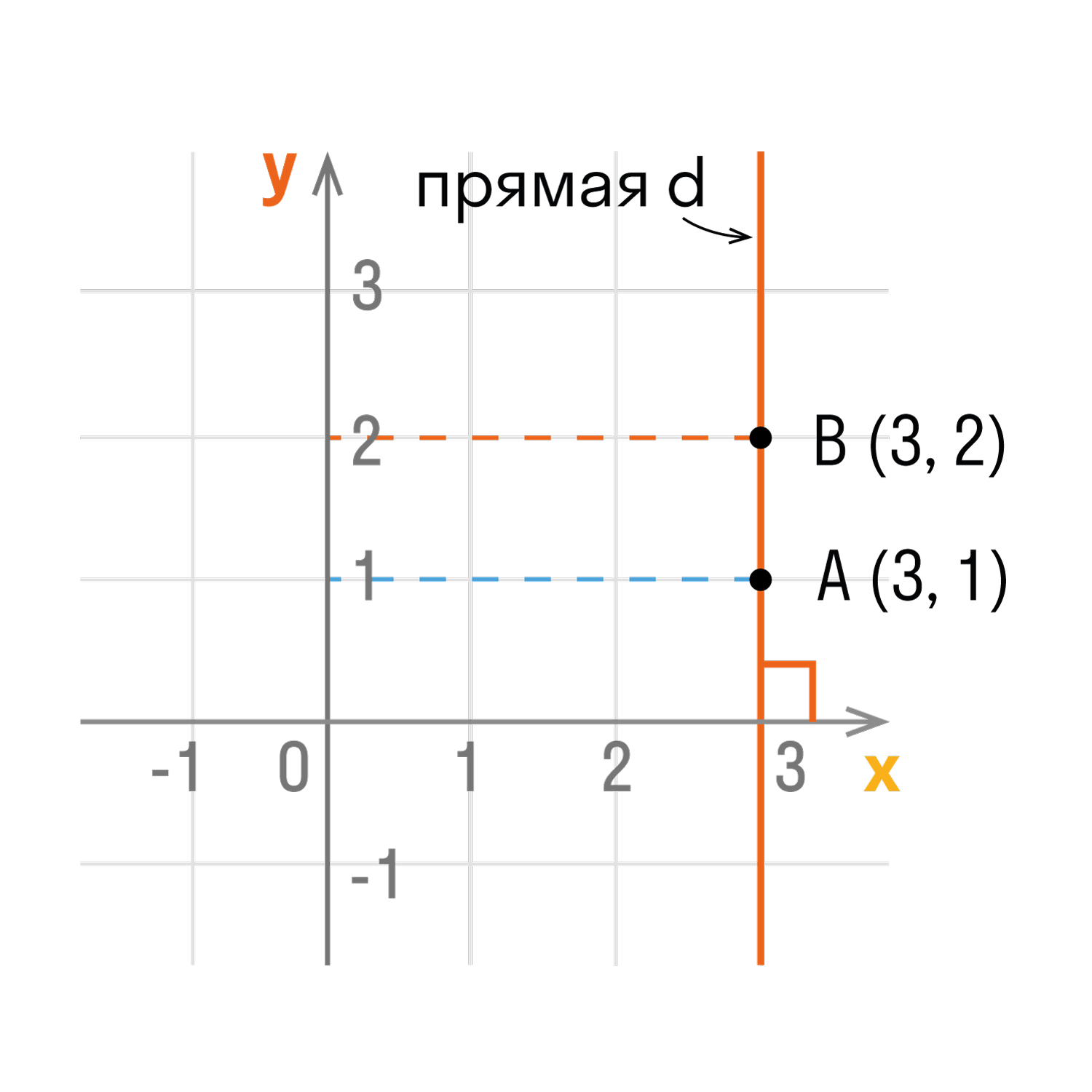
Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
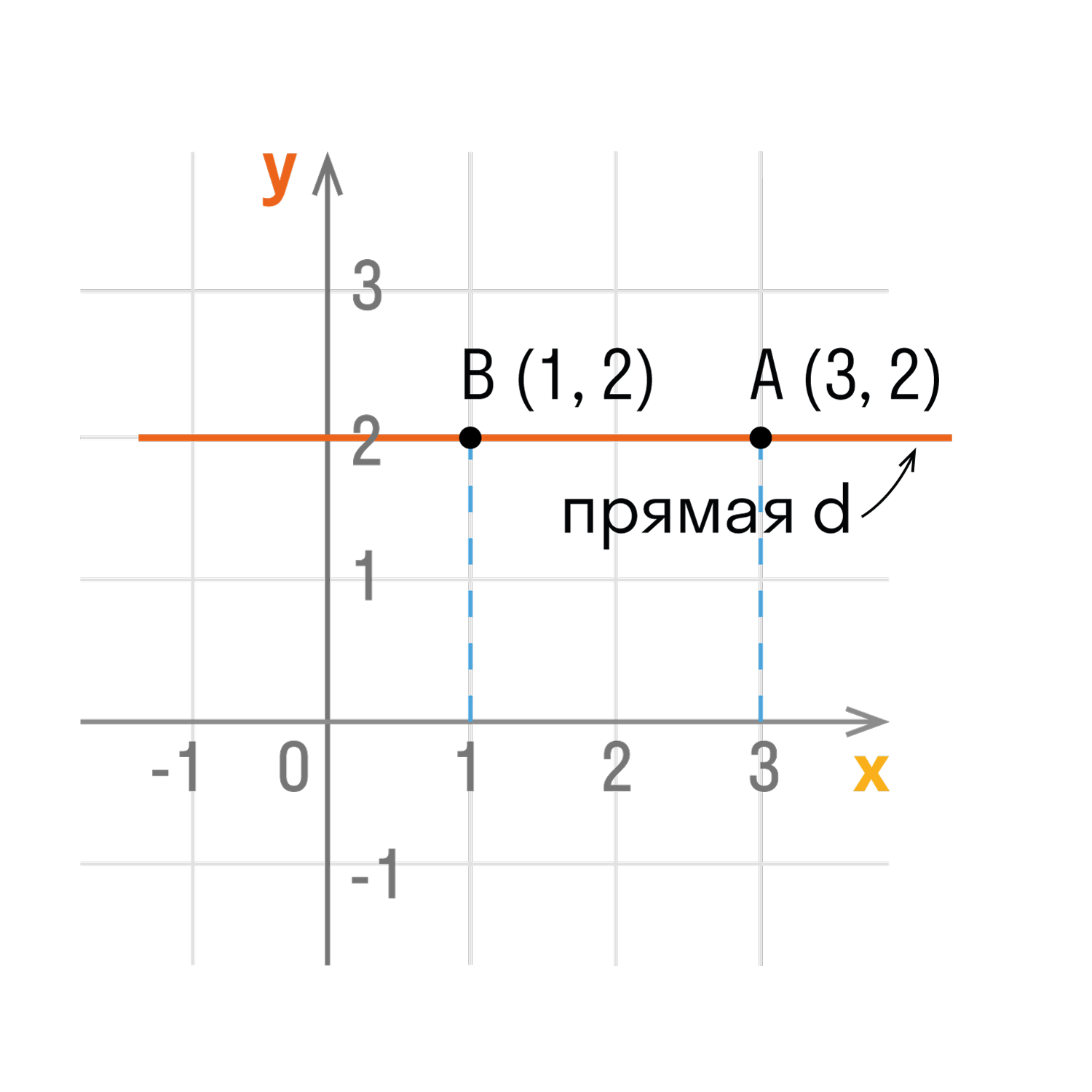
Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).

Видео:Уравнение окружности (1)Скачать

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

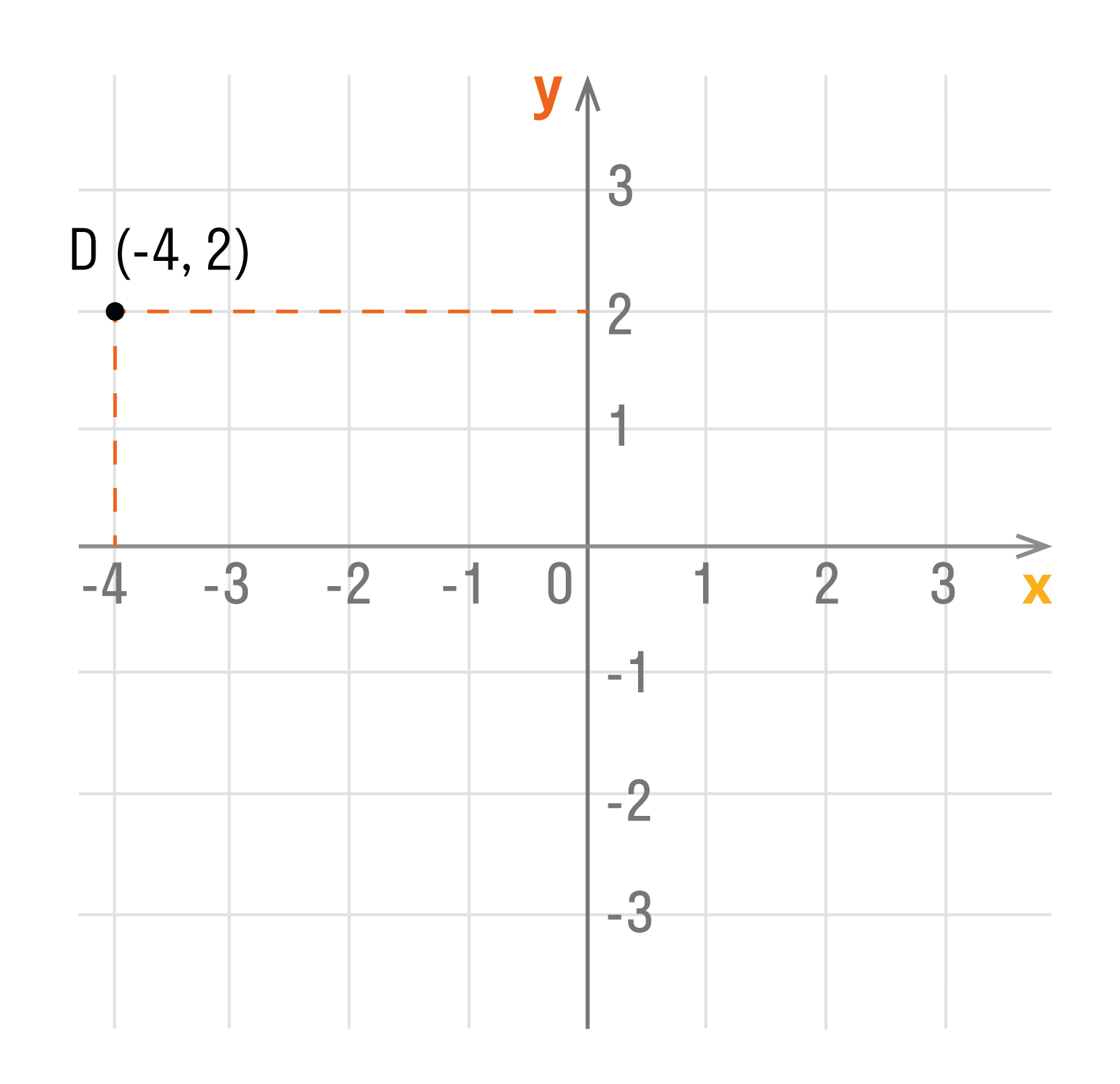
Способ первый. Как определить положение точки D по её координатам (-4, 2):

Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.

Способ второй. Как определить положение точки D (-4, 2):

Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус.
Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.