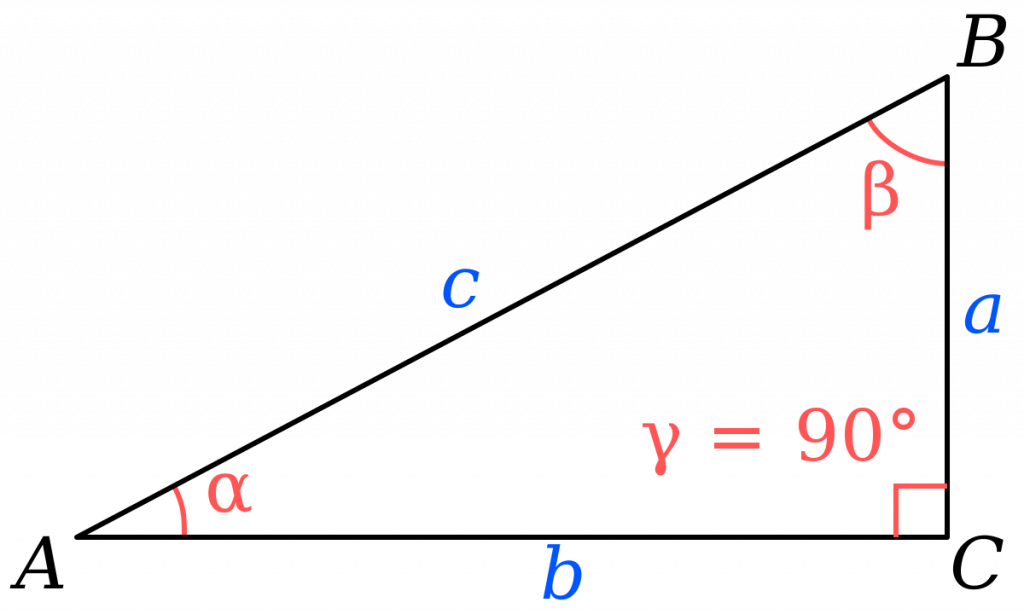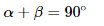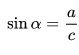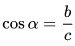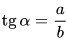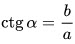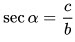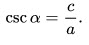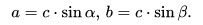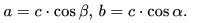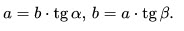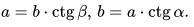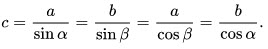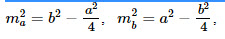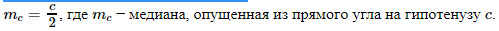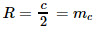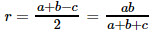Все формулы прямоугольного треугольника

гипотенузу или катеты в прямоугольном треугольнике.

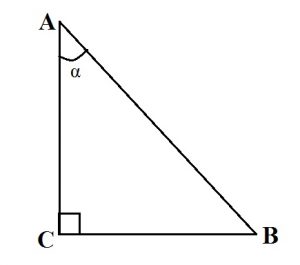
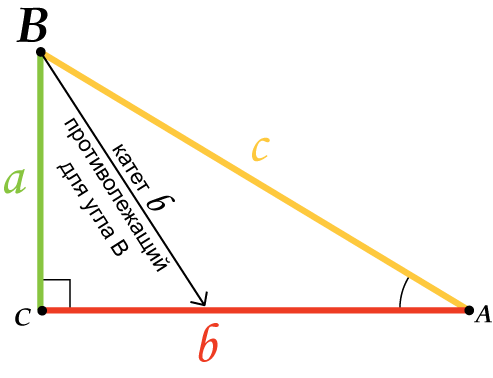
a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Прямоугольный треугольник формулы

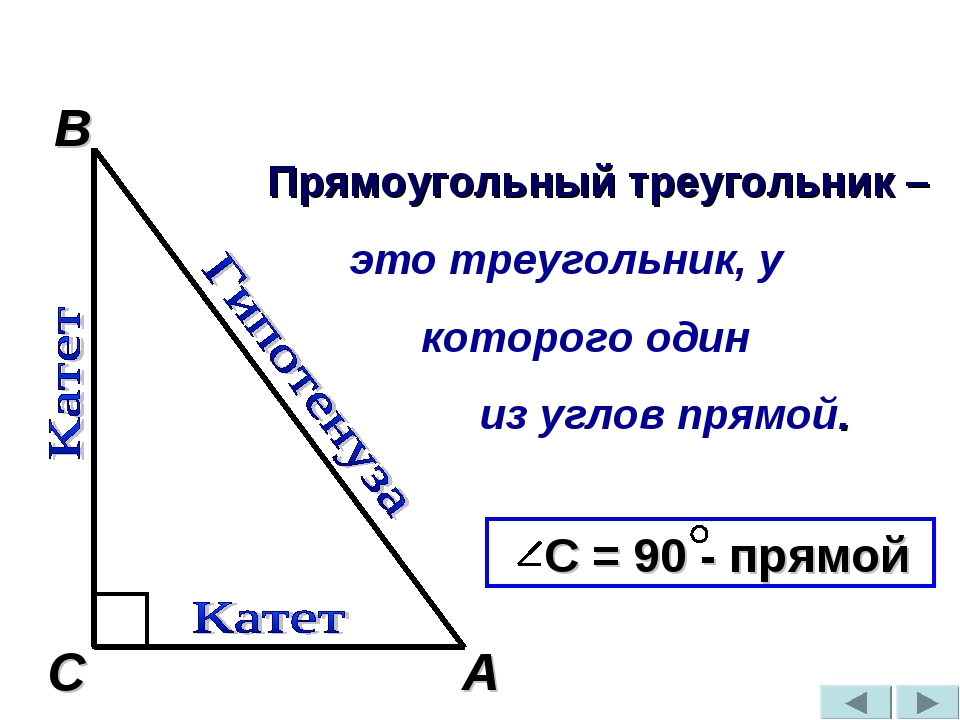
Треугольник называется прямоугольным, если у него один из углов является прямым. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая напротив прямого угла, гипотенузой.

Прямоугольный треугольник: основные формулы

Прямоугольный треугольник: формулы площади и проекции

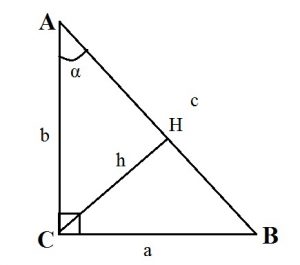
1. Высота прямоугольного треугольника, проведенная к гипотенузе, равна : h = (ab):c.
2. Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу: CH 2 = AH·BH.
3. Катет прямоугольного треугольника — среднее пропорциональное или среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу: CA 2 = AB·AH; CB 2 = AB·BH.
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине.
5. Площадь прямоугольного треугольника равна половине произведения катетов. S = (ab):2.
6. Площадь прямоугольного треугольника равна половине произведения гипотенузы и высоты. S = (hc):2.

Прямоугольный треугольник: формулы тригонометрия

1. Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе. cosα = AC: AB.
2. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. sinα = BC:AB.
3. Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. tgα = BC:AC.
4. Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему. ctgα = AC:BC.
5. Основное тригонометрическое тождество: cos 2 α + sin 2 α = 1.
6. Теорема косинусов: b 2 = a 2 + c 2 – 2ac·cosα.
7. Теорема синусов: CB :sinA = AC : sinB = AB.

Прямоугольный треугольник: формулы для описанной окружности

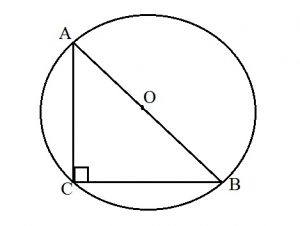
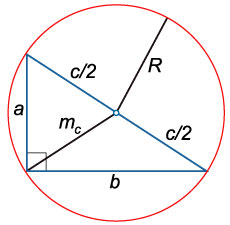
1. Радиус описанной окружности равен половине гипотенузы : R=AB:2.
2. Центр описанной окружности лежит на середине гипотенузы.

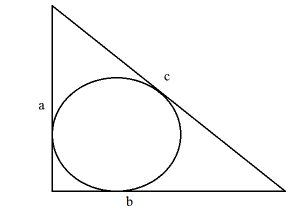
Прямоугольный треугольник: формулы для вписанной окружности

Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле: r = (a + b -c):2.

Рассмотрим применение тригонометрических формул прямоугольного треугольника при решении задания 6(вариант 32) из сборника для подготовки к ЕГЭ по математике профиль автора Ященко.

В треугольнике ABC угол С равен 90°, sinA = 11/14, AC =10√3. Найти АВ.

1. Применяя основное тригонометрическое тождество, найдем cosA = 5√3/14.
2. По определению косинуса острого угла прямоугольного треугольника имеем: cosA = AC : AB, AB = AC : cosA = 10√3·14:5√3 = 28.

Видео:Все свойства и формулы прямоугольного треугольникаСкачать

Все формулы прямоугольного треугольника — примеры расчетов

Видео:Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Формулы

1. Сумма острых углов прямоугольного треугольника равна 90 0 :

2. Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе:

3. Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе:

4. Тангенс острого угла равен отношению противолежащего катета к прилежащему катету:

5. Котангенс острого угла равен отношению прилежащего катета к противолежащему катету:

6. Секанс острого угла равен отношению гипотенузы к прилежащему катету:

7. Косеканс острого угла равен отношению гипотенузы к противолежащему:

8. Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла:

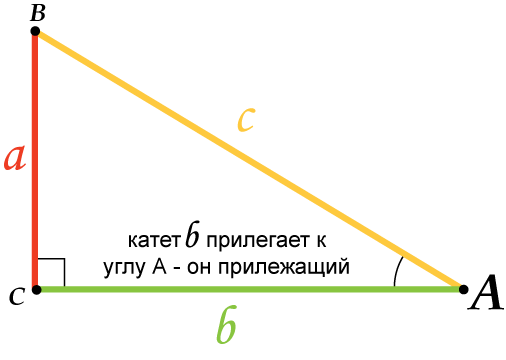
9. Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла:

10. Катет, противолежащий углу, равен произведению второго катета на тангенс угла:

11. Катет, прилежащий углу, равен произведению второго катета на котангенс угла:

12. Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними):

13. Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

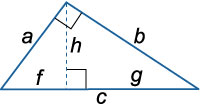
14. Медианы, проведенные к катетам прямоугольного треугольника:

15. Медиана, проведенная к гипотенузе:

16. Радиус окружности, описанной около прямоугольного треугольника:

17. Радиус окружности, вписанной в прямоугольный треугольник:

18. Площадь прямоугольного треугольника равна половине произведения катетов треугольника:

📺 Видео

Все формулы, связанные с прямоугольным треугольникомСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Основное тригонометрическое тождество. 8 класс.Скачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Теорема Пифагора для чайников)))Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Все формулы площади треугольниковСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать

Математика | Метрические соотношения в прямоугольном треугольникеСкачать

Высота прямоугольного треугольникаСкачать

ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Нахождение стороны прямоугольного треугольникаСкачать

8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать