| Фигура | Рисунок | Формулировка | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Треугольник |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Большая сторона треугольника |  | Против большей стороны треугольника лежит больший угол | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Больший угол треугольника | Против большего угла треугольника лежит большая сторона | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньшая сторона треугольника |  | Против меньшей стороны треугольника лежит меньший угол | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньший угол треугольника | Против меньшего угла треугольника лежит меньшая сторона | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Длины сторон треугольника |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Углы треугольника |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешний угол треугольника |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Больший угол треугольника |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньший угол треугольника |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теорема косинусов |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теорема синусов |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Треугольник | |||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||
| Большая сторона треугольника | |||||||||||||||||||||||||||||||
 | Против большей стороны треугольника лежит больший угол | ||||||||||||||||||||||||||||||
| Больший угол треугольника | |||||||||||||||||||||||||||||||
 | Против большего угла треугольника лежит большая сторона | ||||||||||||||||||||||||||||||
| Меньшая сторона треугольника | |||||||||||||||||||||||||||||||
 | Против меньшей стороны треугольника лежит меньший угол | ||||||||||||||||||||||||||||||
| Меньший угол треугольника | |||||||||||||||||||||||||||||||
 | Против меньшего угла треугольника лежит меньшая сторона | ||||||||||||||||||||||||||||||
| Длины сторон треугольника | |||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||
| Углы треугольника | |||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||
| Внешний угол треугольника | |||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||
| Больший угол треугольника | |||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||
| Меньший угол треугольника | |||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||
| Теорема косинусов | |||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||
| Теорема синусов | |||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||
| Треугольник |
 |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.
Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Свойство большей стороны треугольника:
Против большей стороны треугольника лежит больший угол

Свойство большего угла треугольника:
Против большего угла треугольника лежит большая сторона

Свойство меньшей стороны треугольника:
Против меньшей стороны треугольника лежит меньший угол

Свойство меньшего угла треугольника:
Против меньшего угла треугольника лежит меньшая сторона

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.
a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Свойство углов треугольника:
Сумма углов треугольника равна 180°
Свойство внешнего угла треугольника:
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Свойство большего угла треугольника:
Величина большего угла треугольника не может быть меньшей, чем 60°.

где α – больший угол треугольника.

Свойство меньшего угла треугольника:
Величина меньшего угла треугольника не может быть большей, чем 60°.

где β – меньший угол треугольника.


Свойство меньшего угла треугольника:

- Треугольник. Формулы и свойства треугольников.
- Типы треугольников
- По величине углов
- По числу равных сторон
- Вершины углы и стороны треугольника
- Свойства углов и сторон треугольника
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Биссектрисы треугольника
- Свойства биссектрис треугольника:
- Формулы биссектрис треугольника
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Связь между вписанной и описанной окружностями треугольника
- Средняя линия треугольника
- Свойства средней линии треугольника
- Периметр треугольника
- Формулы площади треугольника
- Формула Герона
- Равенство треугольников
- Признаки равенства треугольников
- Первый признак равенства треугольников — по двум сторонам и углу между ними
- Второй признак равенства треугольников — по стороне и двум прилежащим углам
- Третий признак равенства треугольников — по трем сторонам
- Подобие треугольников
- Признаки подобия треугольников
- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- Треугольник. Формулы определения и свойства треугольников.
- Определение треугольника
- Классификация треугольников
- 1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
- 2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
- 3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
- 4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
- 5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
- 6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
- Свойства треугольника
- 1.Свойства углов и сторон треугольника.
- 2.Теорема синусов.
- 3. Теорема косинусов.
- 4. Теорема о проекциях
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- 🌟 Видео
Видео:Найдите сторону треугольника на рисункеСкачать

Треугольник. Формулы и свойства треугольников.
Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Типы треугольников
По величине углов
По числу равных сторон
Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Видео:Нахождение стороны прямоугольного треугольникаСкачать

Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Видео:Геометрия Найдите наибольшую высоту треугольника со сторонами 11 см 25 см и 30 смСкачать

Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Видео:Почти никто не решил ➜ Найдите сторону треугольникаСкачать

Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Видео:Найдите третью сторону треугольникаСкачать

Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Видео:Задача про стороны треугольника. Геометрия 7 класс.Скачать

Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Видео:Задача про соотношение сторон. Геометрия 7 класс.Скачать

Связь между вписанной и описанной окружностями треугольника
Видео:Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать

Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Видео:наибольшая и наименьшая стороны треугольника. Углы треугольника #углы #треугольникСкачать

Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
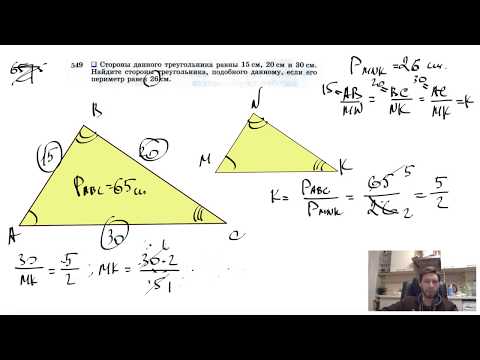
Видео:№549. Стороны данного треугольника равны 15 см, 20 см и 30 см. Найдите стороны треугольникаСкачать
Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Уравнения стороны треугольника и медианыСкачать

Треугольник. Формулы определения и свойства треугольников.
В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Определение треугольника
Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Треугольник ABC (△ABC)
- Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.
Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:
Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Классификация треугольников
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Видео:Найдите стороны треугольникаСкачать

Свойства треугольника
1.Свойства углов и сторон треугольника.
- Сумма всех углов треугольника равна 180°:
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема о проекциях
Для остроугольного треугольника:
Видео:ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

Медианы треугольника
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
5. Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны:
🌟 Видео
Определить вид треугольника по сторонам. 9 классСкачать