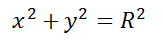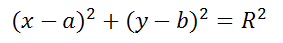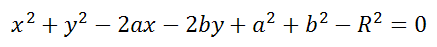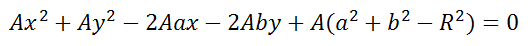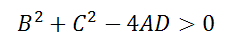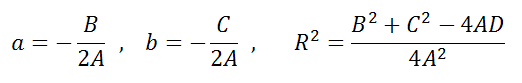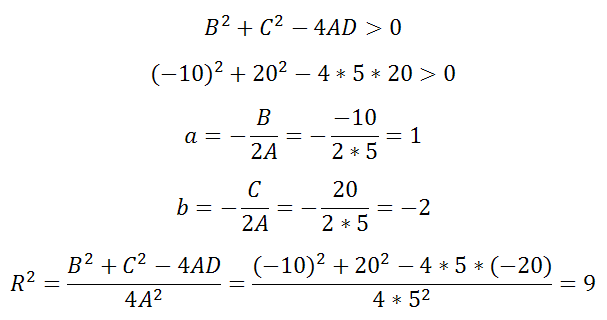Как определить координаты точки на окружности

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

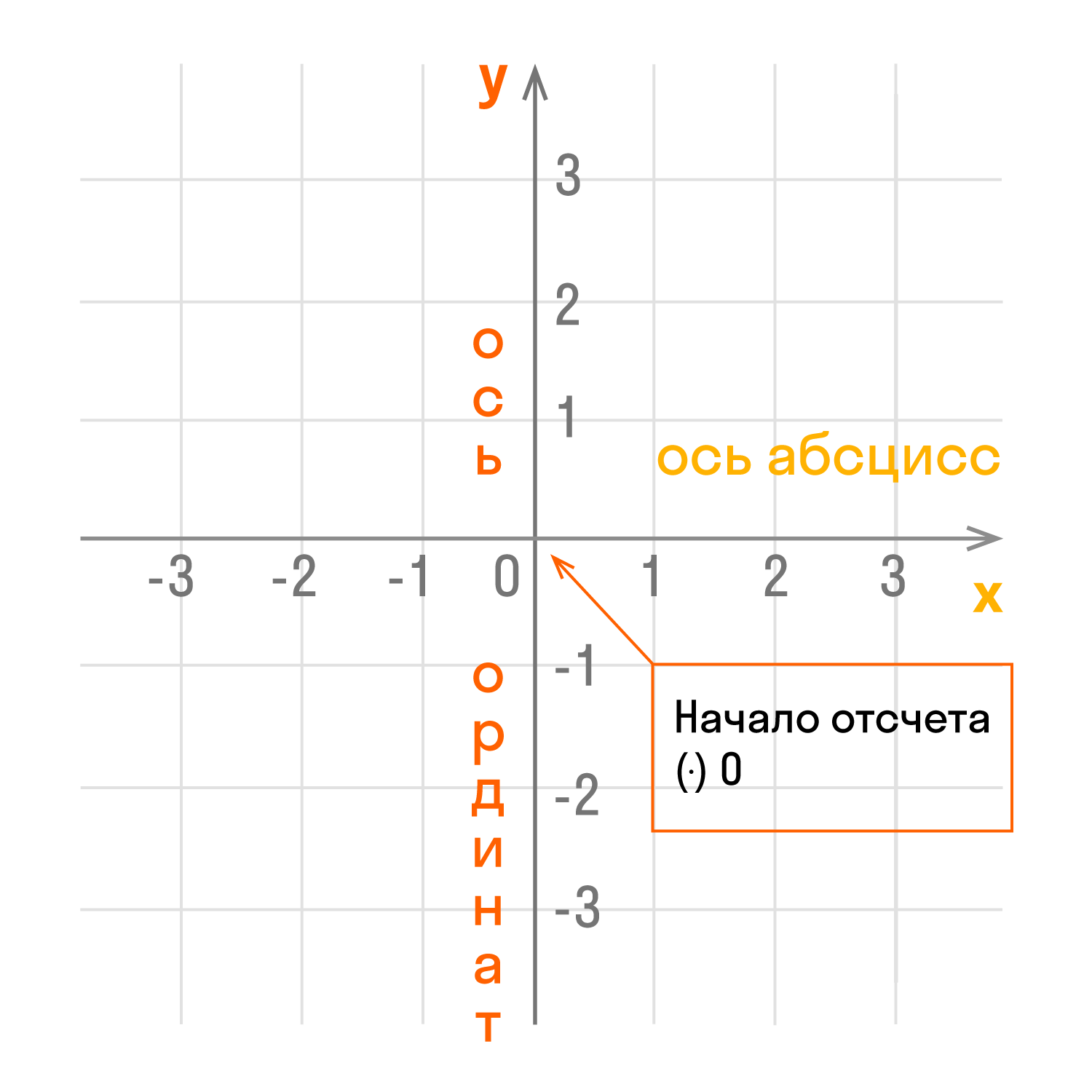
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

• Координатные оси — это прямые, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

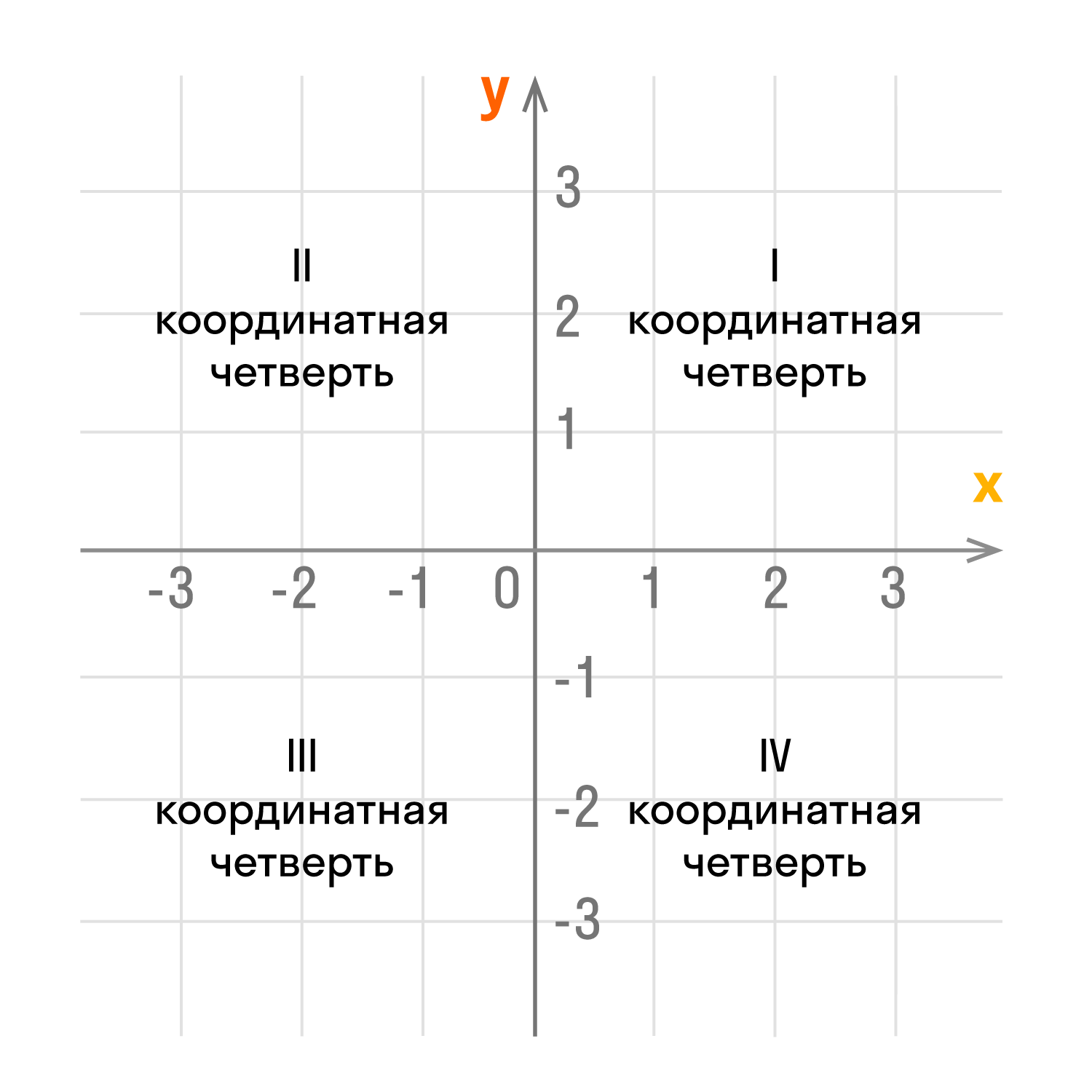
Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Видео:Как искать точки на тригонометрической окружности.Скачать

Определение координат точки

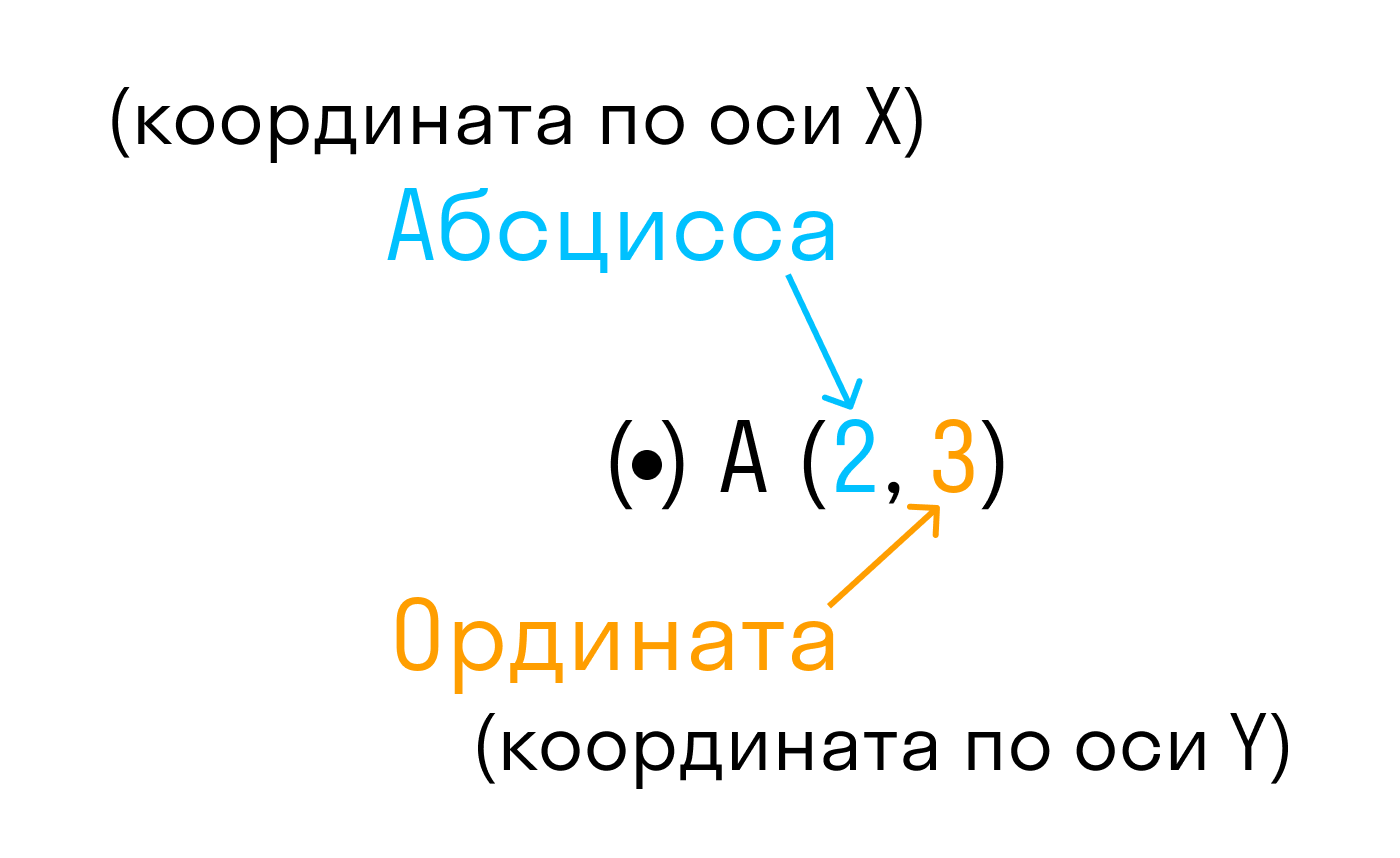
Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

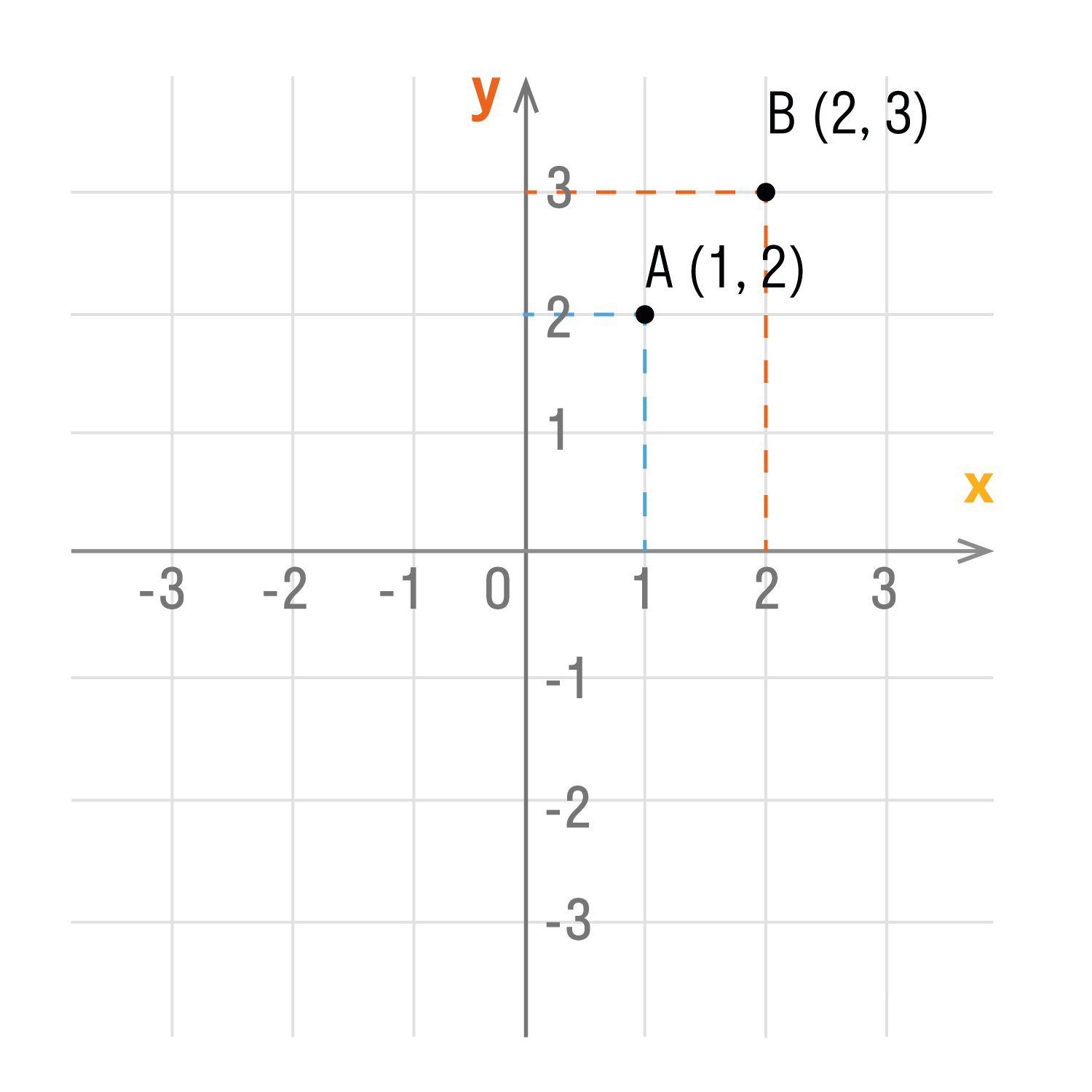
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Видео:Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

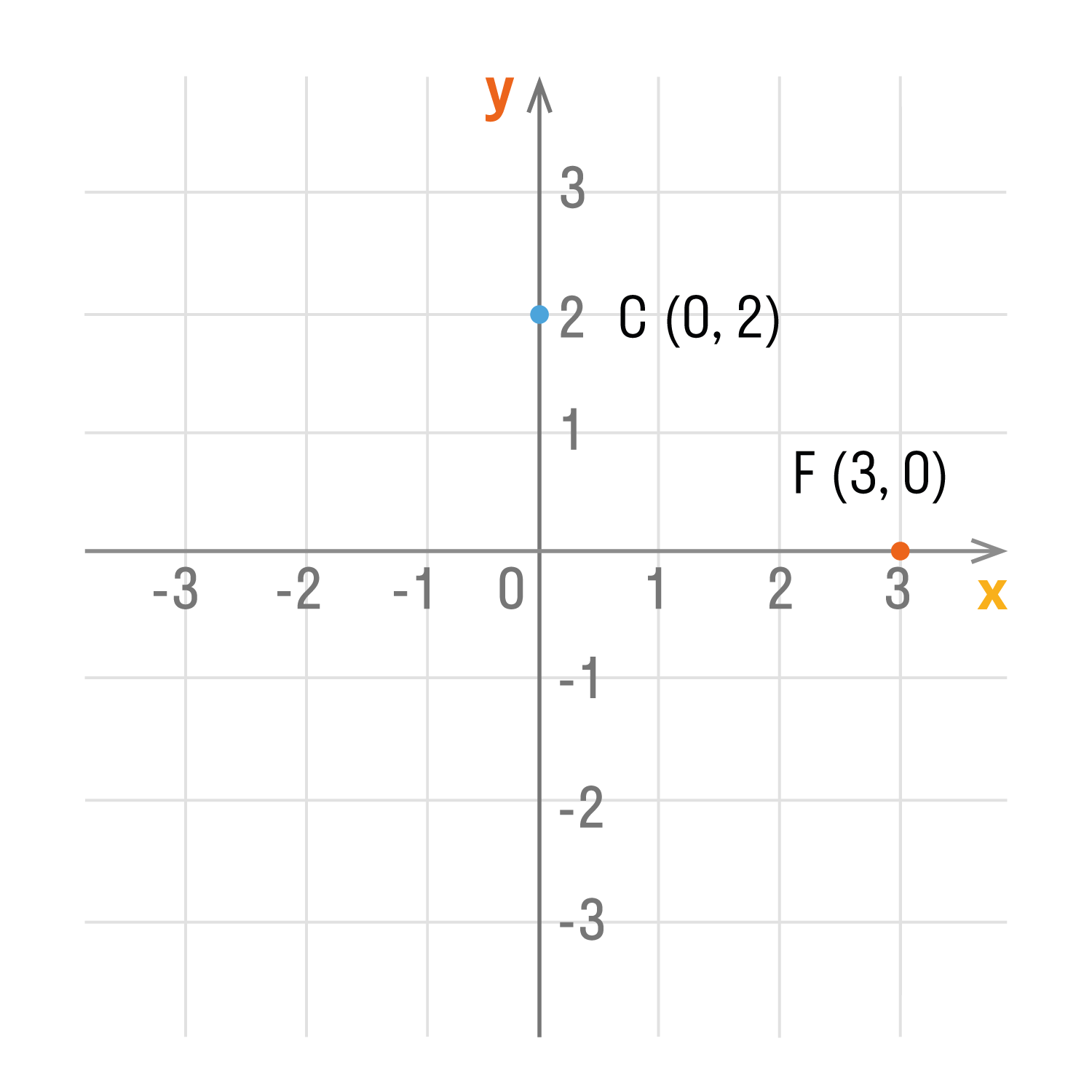
1. Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
   точка С (0, 2).
2. Если точка лежит на оси Ox, то ее ордината равна 0. Например,
   точка F (3, 0).
3. Начало координат — точка O. Ее координаты равны нулю: O (0,0).
   
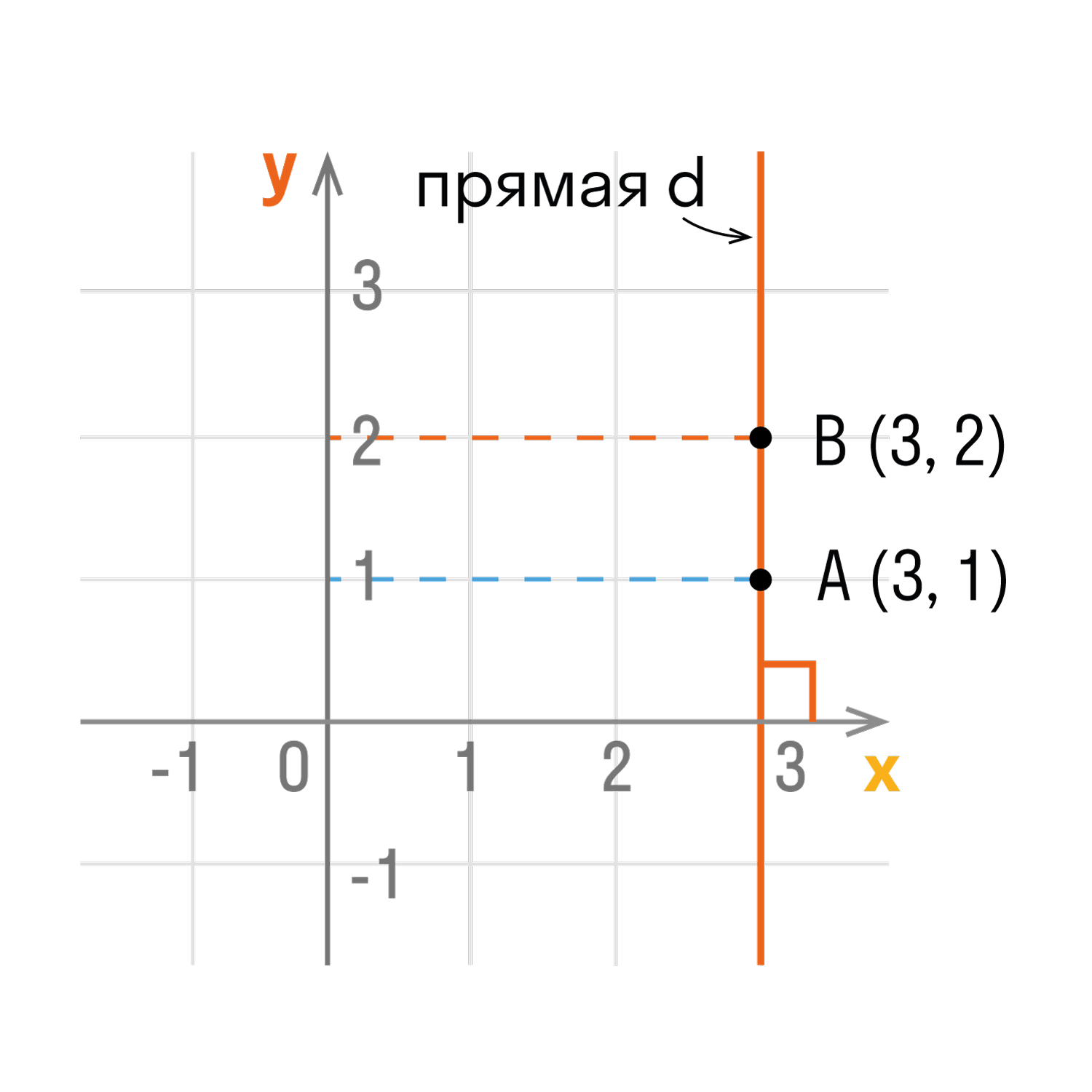
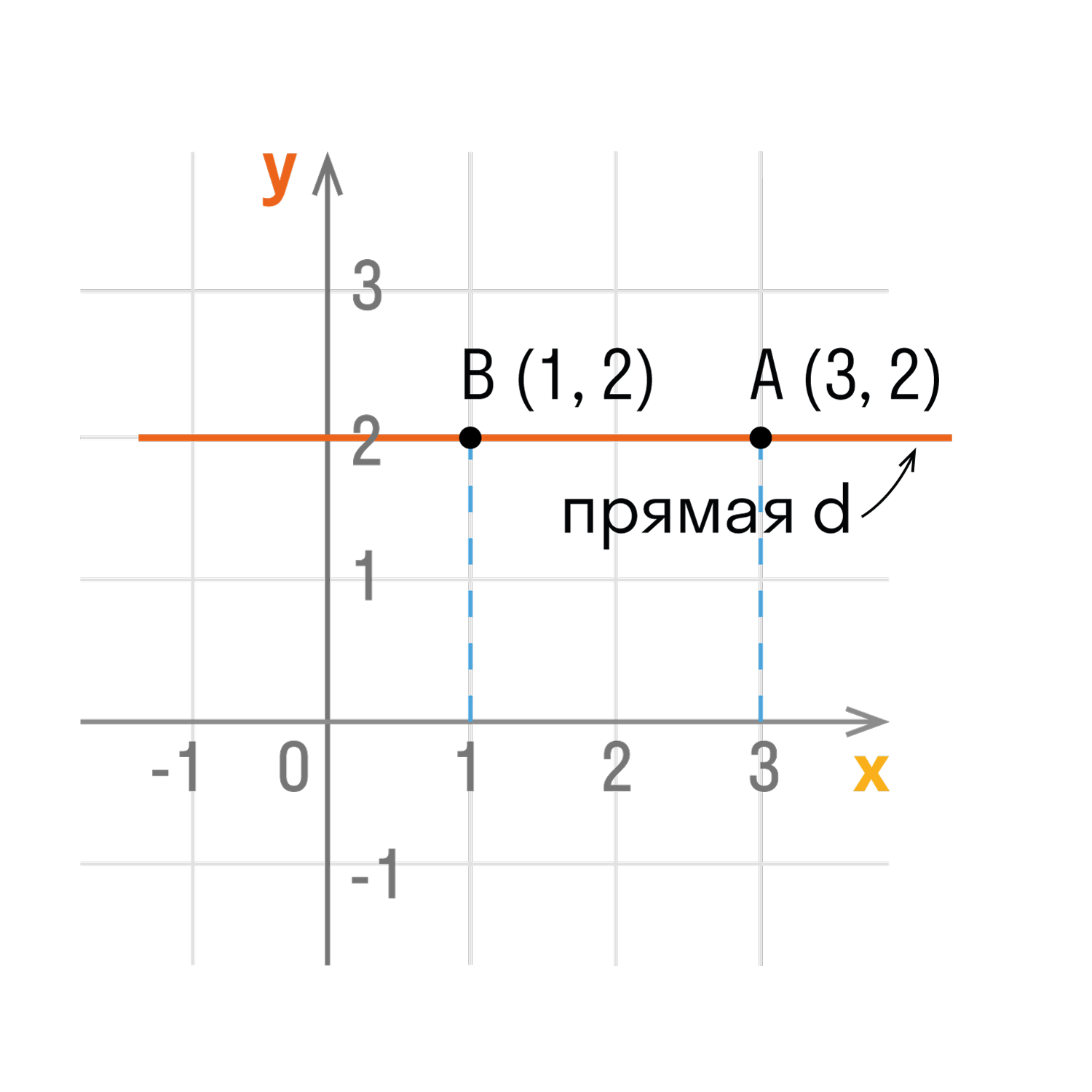
4. Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
   
5. Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
   
6. Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
   
7. Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
   

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

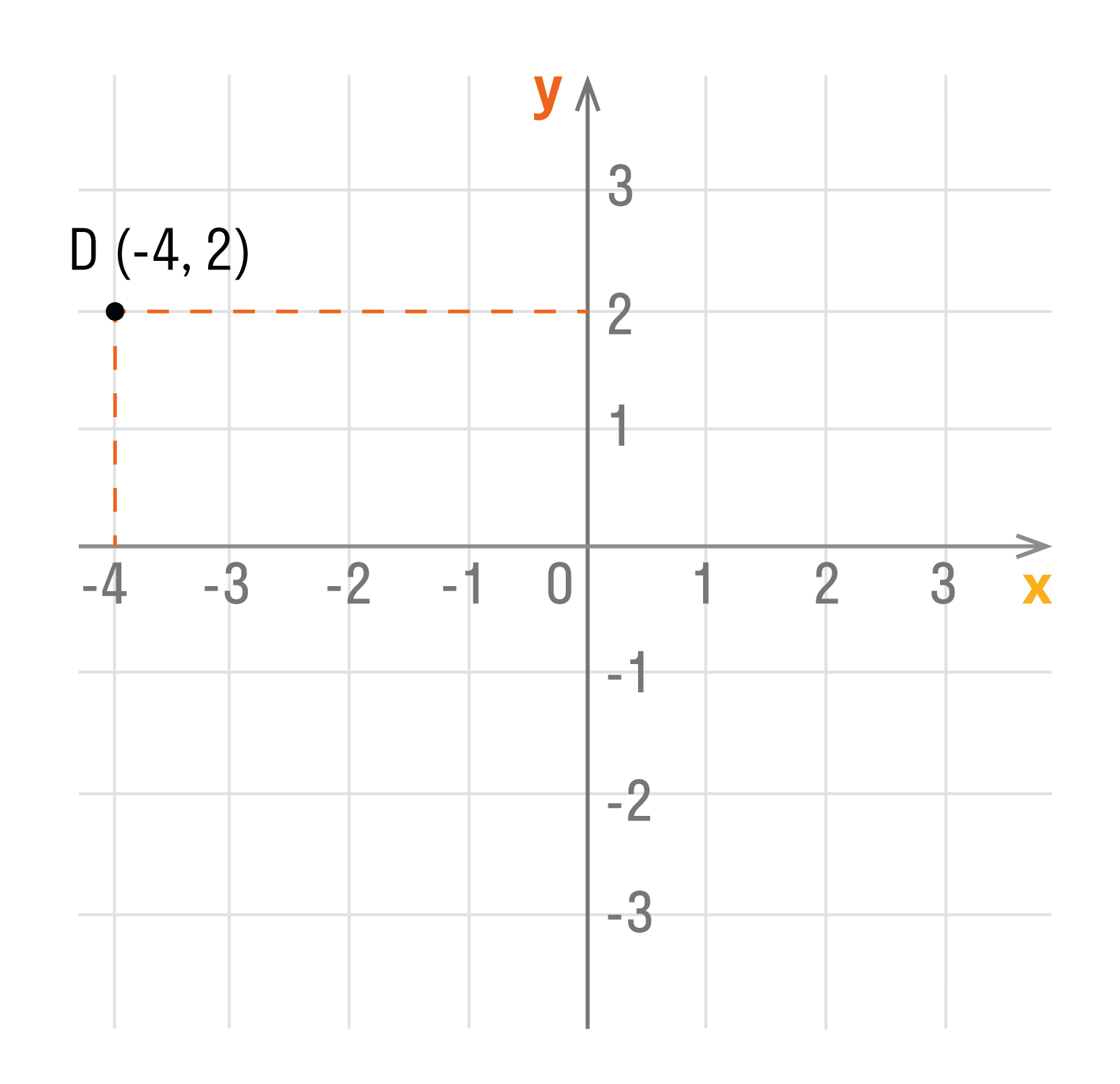
Способ первый. Как определить положение точки D по её координатам (-4, 2):

1. Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
2. Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
3. Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
   

Способ второй. Как определить положение точки D (-4, 2):

1. Сместить прямую по оси Ox влево на 4 единицы, так как у нас
   перед 4 стоит знак минус.
2. Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
   

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Видео:Тригонометрическая окружность. Как выучить?Скачать

Как найти координату точки окружности

Видео:Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать

Как находить точки окружности

Окружность изучается в геометрии, и чтобы правильно сделать заданную задачу, нужно научиться находить точки окружности. Для этого вам понадобится список необходимых инструментов, таких как:

• простой карандаш;
• тетрадь в клеточку;
• циркуль;
• транспортир;
• шариковая или гелевая ручка.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Как найти координаты точки окружности

Прежде, чем найти точку на окружности и обозначить ее координаты, следует эту окружность построить. При построении вам встретятся еще несколько правил, в зависимости от заданных в задаче вопросов. Это может быть как хорда, на которой тоже нужно будет найти точку в окружности, она соединяет две точки. Помните, что диаметром называется хорда, которая проходит через центр окружности и соединяет две противоположные точки на ней.

Также можно найти точку на окружности, которая находится на касательной, то есть прямой, которая имеет с окружностью одну общую точку, но не пересекает ее. Если окружность пересекается прямой, то она имеет с ней две общие точки, найти на окружности их легко, так как они одновременно относятся как к окружности, так и к прямой. Для определения координат точки на окружности можно воспользоваться как формулой для прямой, так и формулой для окружности.

Как найти координаты точки на окружности или, если известно только значение радиуса R, можно по одной из его координат, либо если дано значение угла альфа. Выглядит это так:

sin alpha = y / R
cos alpha = x / R
cos alpha * cos alpha + sin alpha * sin alpha = 1

Может помочь также найти на окружности координаты точки один из многочисленных форумов, где сидят математики и помогают решить все задачки, но не только помогают, но и стараются объяснить ее.

В школе учат, как найти точки окружности, когда начинают изучать геометрию в 6 классе.

Отличников, которые знают, как найти точки на окружности и их координаты, часто могут обижать в школе, если они не дают списывать. В таких случаях будет нелишним знать, как наказать обидчика за оскорбление.

Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Как найти координаты точки?

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:Координаты точки и координаты вектора 1.Скачать

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

• Координатные оси — это прямые, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Видео:Координаты точек на числовой окружности, часть 5. Алгебра 10 класс.Скачать

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Видео:9 класс, 11 урок, Формулы для вычисления координат точкиСкачать

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

1. Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
   точка С (0, 2).
2. Если точка лежит на оси Ox, то ее ордината равна 0. Например,
   точка F (3, 0).
3. Начало координат — точка O. Ее координаты равны нулю: O (0,0).
   
4. Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
   
5. Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
   
6. Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
   
7. Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
   

Видео:В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

1. Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
2. Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
3. Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
   

Способ второй. Как определить положение точки D (-4, 2):

1. Сместить прямую по оси Ox влево на 4 единицы, так как у нас
   перед 4 стоит знак минус.
2. Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
   

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Окружность на координатной плоскости

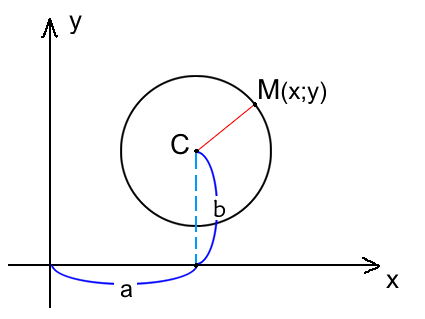
Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Окружность радиуса R с центром в начале координат представляется уравнением:

Окружность радиуса R с центром в точке C(a;b) представляется уравнением:

Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия ).
Это уравнение можно записать в виде:

Если уравнение помножить на любое число A, то получим

Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.

Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x 2 и y 2 были равны в уравнение вида:

3. Если выполняется неравенство

Видео:Найти координаты точки окружности заданного радиуса Д301Скачать

Как найти радиус и центр окружности

Уравнение Ax 2 +Bx+Ay 2 +Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:

Пример 1
Уравнение 5x 2 -10x+5y 2 +20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство

Решая, получаем что центр есть (1;-2), а радиус R=3

Анимационный график окружности

Пример 2
Уравнение второй степени x 2 +4xy+y 2 =1 не является окружностью, так как в нём есть член 4xy.

Пример 3
Уравнение второй степени 4x 2 +9y 2 =36 не представляет окружность, так как в нём коэффициенты при x 2 и y 2 не равны.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.3 / 5. Количество оценок: 4

Видео:Уравнение окружности (1)Скачать

Уравнение окружности.

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:

Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Видео:Алгебра 10 класс. 22 сентября. Числовая окружность #8 координаты точек 2Скачать

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x — 2 ) 2 + (y — ( -3 )) 2 = 4 2
или
(x — 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16.

Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 — 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

🌟 Видео

Координаты точек на числовой окружности, часть 2. Алгебра 10 класс.Скачать

Попадание точки в заданную область. Два сектора. Уроки программирования на С++.Скачать

Координаты вектора. 9 класс.Скачать