Свойства треугольников.
Меню
Треугольник -это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Для инженера это еще и единственная «жесткая» плоская фигура на свете.
Раздел математики, посвященный изучению закономерностей треугольников — тригонометрия.
Сумма всех углов в треугольнике равна 180°.
- Обозначения в треугольнике..
- Виды треугольников:
- Основные свойства треугольников. В любом треугольнике:
- Конгруэнтные треугольники = равные треугольники.
- Признаки равенства треугольников:
- Признаки равенства прямоугольных треугольников:
- Подобные треугольники.
- Признаки подобия треугольников:
- Свойства подобных треугольников.
- Подобие в прямоугольных треугольниках.
- Теорема Пифагора.
- Теоремы синусов и косинусов.
- Теорема синусов.
- Теорема косинусов.
- Основные линии треугольника.
- Медиана.
- Свойства медиан треугольника.
- Биссектриса
- Свойства биссектрисы угла треугольника
- Высота треугольника
- Свойства высот треугольника
- Срединный перпендикуляр
- Свойства срединных перпендикуляров треугольника.
- Средняя линия
- Свойство средней линии треугольника
- Формулы площади треугольника
- 1.Произвольный треугольник — формулы площади
- Прямоугольный треугольник — площадь
- Равносторонний (правильный) треугольник — площадь
- Примечание — в прямоугольном треугольнике:
- Прямоугольный треугольник
- Прямоугольный треугольник. Теорема Пифагора.
- теория по математике 📈 планиметрия
- Свойства прямоугольного треугольника
- Признаки равенства прямоугольных треугольников
- Теорема Пифагора
- Египетский треугольник
- Пифагоровы тройки
- 🎬 Видео
Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

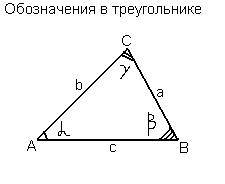
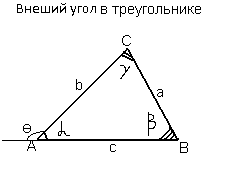
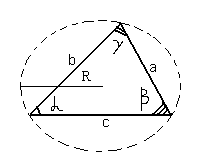
Обозначения в треугольнике..
Вершины треугольника обычно обозначаются заглавными латинскими буквами (A, B, C), величины углов при соответственных вершинах — греческими буквами (α, β, γ), а длины противоположных сторон — прописными латинскими буквами (a, b, c).
Видео:Нахождение стороны прямоугольного треугольникаСкачать

Виды треугольников:
(по величине углов)
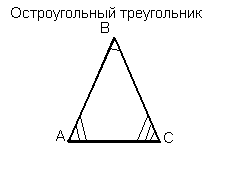 Остроугольный треугольник — это треугольник, в котором все три угла острые, т.е. меньше 90°.
Остроугольный треугольник — это треугольник, в котором все три угла острые, т.е. меньше 90°.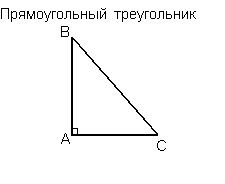
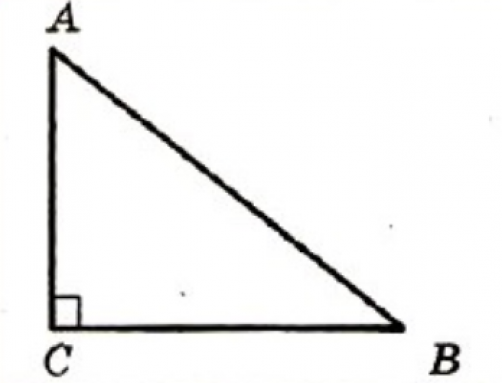
Прямоугольный треугольник — это треугольник, содержащий прямой угол.
Две стороны, образующие прямой угол, называются катетами (АС и АВ), а сторона, противолежащая прямому углу, называется гипотенузой (ВС).
Тупоугольный треугольник — это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°.
(по числу равных сторон)
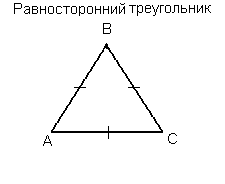
Равносторонний (правильный) треугольник — это треугольник, у которого все стороны и все углы равны (каждый угол равен 60°).
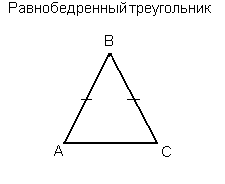
Равнобедренный тругольник — это треугольник, у которого два угла и две стороны равны.
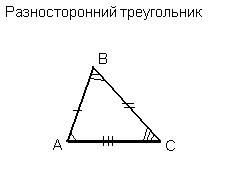
Разносторонний треугольник — это треугольник, в котором все углы, а значит и все стороны попарно различны.
(Разносторонний треугольник может быть остроугольным, прямоугольным и тупоугольным).
Рассмотрим рис. ниже.
Углы α, β, γ нызываются внутренними углами треугольника.
Угол Θ — называется внешним углом треугольника, он равен сумме двух противолежащих ему внутренних углов, т.е. Θ= β+γ
(а+с+b) — периметр треугольника.
Угол α, называется смежным по отношению к углу Θ. ( α+ Θ)=180° (развернутый угол)
Основные свойства треугольников. В любом треугольнике:
Против большей стороны лежит больший угол, и наоборот.
Против равных сторон лежат равные углы, и наоборот. (В частности, все углы в равностороннем треугольнике равны.)
Сумма углов треугольника равна 180 ° (Из двух последних свойств следует, что каждый угол в равностороннем треугольнике равен 60 °).
Продолжая одну из сторон треугольника (AВ), получаем внешний угол Θ.
Любая сторона треугольника меньше суммы двух других сторон и больше их разности:
- a b – c;
- b a – c;
- c a – b.
|
|
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

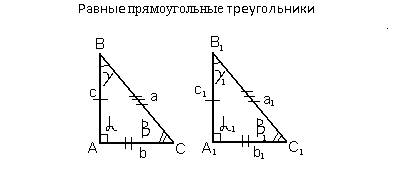
Конгруэнтные треугольники = равные треугольники.
Два треугольника называются конгруэнтными (равными), если они равны по всем параметрам, т.е. три угла и три стороны одного треугольника равны трем углам и трем сторонам другого треугольника.
Видео:Теорема Пифагора для чайников)))Скачать

Признаки равенства треугольников:
Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Признаки равенства прямоугольных треугольников:
Два прямоугольных треугольника равны, если у них соответственно равны:
1. Гипотенуза и острый угол.
2. Катет и противолежащий угол.
3. Катет и прилежащий угол.
4. Два катета.
5. Гипотенуза и катет.
Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

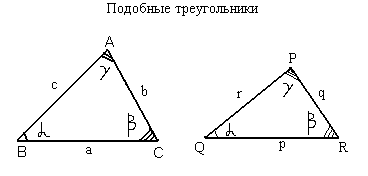
Подобные треугольники.
Два треугольника являются подобными, если углы одного треугольника равны, углам тругого треугольника, а стороны подобны, т.е.
Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Признаки подобия треугольников:
- Два угла одного треугольника равны двум углам другого треугольника.
- Две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны.
- Три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника.
Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Свойства подобных треугольников.
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия [(р/а)=(q/b)=(r/c)=коэффициент подобия].
- Отношение периметров и длин либо биссектрис, либо медиан, либо высот, либо серединных перпендикуляров равно коэффициенту подобия. т.е. в подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны.
Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

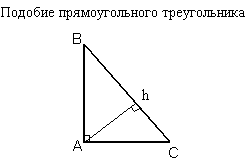
Подобие в прямоугольных треугольниках.
Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:
1. Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому (Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось.) проекций катетов на гипотенузу.
2. Катет равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу.
Видео:8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать

Теорема Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. , т.е. BC 2 =AB 2 +AC 2 см. рис. выше.
Видео:Решение прямоугольных треугольниковСкачать

Теоремы синусов и косинусов.
Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов, причем коэффициент пропорциональности равен диаметру описанной около треугольника окружности:
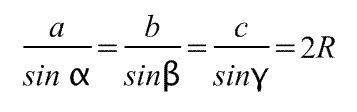
Теорема косинусов.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Основные линии треугольника.
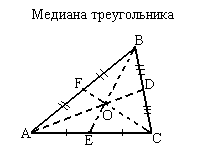
Медиана.
Медиана – это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника AD, CF, BE пересекаются в одной точке O, всегда лежащей внутри треугольника и являющейся центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.
Свойства медиан треугольника.
- Медиана разбивает треугольник на два треугольника одинаковой площади.
- Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
- Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
- Из двух медиан треугольника большая медиана проведена к его меньшей стороне.
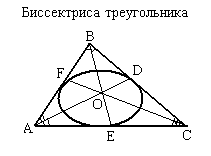
Биссектриса
Биссектриса угла треугольника— это луч, который исходит из вершины треугольника, проходит между его сторонами и делит данный угол пополам. Три биссектрисы треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Свойства биссектрисы угла треугольника
- Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам например, на рис. выше AE:CE = AB:BC
- Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
- Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
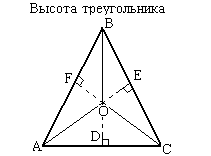
Высота треугольника
Высота треугольника — это перпендикуляр, опущенный из любой вершины на противоположную сторону (или её продолжение). Эта сторона называется основанием треугольника. Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника.Ортоцентр остроугольного треугольника (точка O на рис. выше) расположен внутри треугольника, а ортоцентр тупоугольного треугольника – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.
Свойства высот треугольника
- Прямые, содержащие высоты треугольника пересекаются в одной точке (ортоцентре треугольника).
- Отрезок, соединяющий основания высот остроугольного треугольника, отсекает от данного треугольника подобный ему с коэффициентом подобия, равным косинусу общего угла этих треугольников.
- Из двух высот треугольника большая высота проведена к его меньшей стороне.
- В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
- В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
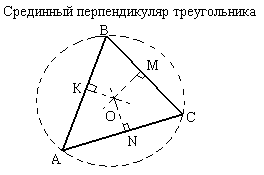
Срединный перпендикуляр
Срединный перпендикуляр – это перпендикуляр, проведенный из средней точки отрезка(стороны). Три срединных перпендикуляра треугольника АВС(KO, MO, NO, рис.выше) пересекаются в одной точке О, являющейся центром описанного круга( точки K, M, N – середины сторон треугольника ABC).
В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.
Свойства срединных перпендикуляров треугольника.
1. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
2. Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Видео:7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

Формулы площади треугольника
1.Произвольный треугольник — формулы площади
a, b, c — стороны; α — угол между сторонами a и b; p=(a+b+c) / 2— полупериметр; R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; ha — высота, проведенная к стороне a.
- S=(1/2)*(a* ha) — по стороне и высоте.
- S=(1/2) *(a*b*sinα) по двум сторонам и синусу угла между ними
— по длинам сторон — формула площади Герона
- S=p*r — через периметр и радиус вписанной окружности
- S=(a*b*c) / (4R) — через длины сторон и радиус описанной оружности
Прямоугольный треугольник — площадь
a, b — катеты; c — гипотенуза; hc — высота, проведенная к стороне c.
Равносторонний (правильный) треугольник — площадь
Примечание — в прямоугольном треугольнике:
— Синус α — это отношение AB/OB (отношение противолежащего катета к гипотенузе)
— Косинус α — это отношение ОА/OB (отношение прилежащего катета к гипотенузе)
— Тангенс α — это отношение AB/OA (отношение противолежащего катета к прилежащему)
— Котангенс α — это отношение ОА/AB (отношение прилежащего катета к противолежащему)
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Прямоугольный треугольник
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Стороны, прилежащие к прямому углу, называются катетами .
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где
– катеты,
– гипотенуза. Видеодоказательство
4. Площадь прямоугольного треугольника с катетами
:
5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты
и гипотенузу
следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус описанной окружности есть половина гипотенузы
:
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус вписанной окружности выражается через катеты
и гипотенузу
следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
Видео:КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Прямоугольный треугольник. Теорема Пифагора.
теория по математике 📈 планиметрия
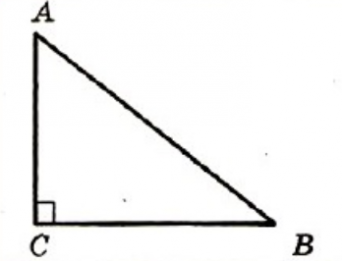
Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.
На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.
Видео:7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать

Свойства прямоугольного треугольника
- В прямоугольном треугольнике гипотенуза является наибольшей стороной.
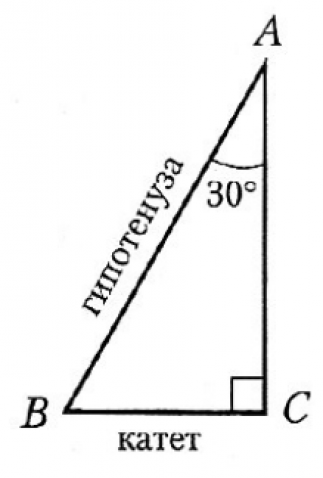
- В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .
Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .
- Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
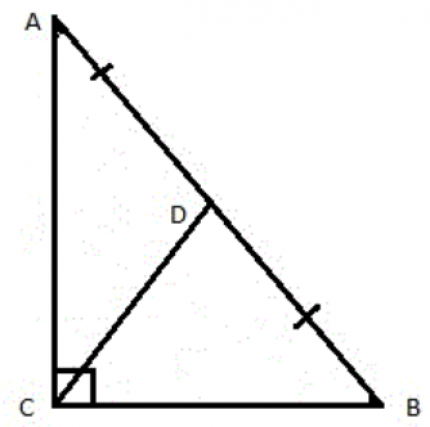
- Медиана, проведенная к гипотенузе, равна её половине.
На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.
Видео:Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Признаки равенства прямоугольных треугольников
Существует 4 признака равенства прямоугольных треугольников:
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:
- по катетам;
- по катету и прилежащему острому углу;
- по гипотенузе и острому углу;
- по гипотенузе и катету.
Видео:Свойства прямоугольного треугольника. Практическая часть. 7 класс.Скачать

Теорема Пифагора
Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2
Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.
Египетский треугольник
Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.
Пифагоровы тройки
Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.
🎬 Видео
Стороны прямоугольного треугольникаСкачать

Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

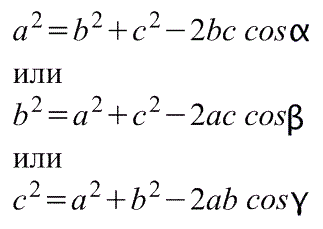
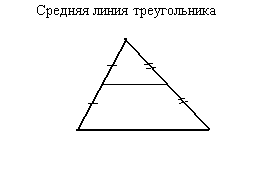
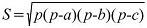 — по длинам сторон — формула площади Герона
— по длинам сторон — формула площади Герона