Как называются прямые на изображении пересекающиеся скрещивающиеся параллельные ответить (3 видео)

5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых

Видеоурок: Параллельные прямые, перпендикулярные к плоскости

Лекция: Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых

Пересекающиеся прямые

Если на плоскости имеются несколько прямых, то они либо рано или поздно пересекутся произвольно, либо под прямым углом, или же будут параллельными. Давайте же разберемся с каждым случаем.

Пересекающимися можно назвать те прямые, у которых будет хотя бы одна точка пересечения.

Вы спросите, почему хотя бы одна, не может же прямая пересечь другую прямую две или три раза. Вы правы! Но прямые могут полностью совпасть друг с другом. В таком случае общих точек будет бесконечное множество.

Параллельность

Параллельными можно назвать те прямые, которые никогда не пересекутся, даже на бесконечности.

Иными словами, параллельные – это те, у которых нет ни одной общей точки. Обратите внимание на то, что данное определение справедливо только в том случае, если прямые находятся в одной плоскости, если же они не имеют общих точек, находясь в разных плоскостях, то они считаются скрещивающимися.

Примеры параллельных прямых в жизни: два противоположных края экрана монитора, линии в тетрадях, а также многие другие части вещей, имеющих квадратную, прямоугольную и другие формы.

Когда хотят показать на письме, что одна прямая параллельная второй, то используют следующее обозначение a||b. Данная запись говорит, что прямая а параллельна прямой b.

При изучении данной темы важно понять еще одно утверждение: через некоторую точку на плоскости, которая не принадлежит данной прямой, можно провести единственную параллельную прямую. Но обратите внимание, снова поправка – на плоскости. Если рассматривать трехмерное пространство, то можно провести бесконечное множество прямых, которые не будут пересекаться, но будут скрещивающимися.

Утверждение, которое было описано выше, называется аксиомой о параллельности прямых.

Перпендикулярность

Прямые можно назвать только в том случае перпендикулярными, если они пересекаются под углом, равным 90 градусов.

В пространстве через некоторую точку на прямой можно провести бесконечное множество перпендикулярных прямых. Однако, если речь идет о плоскости, то через одну точку на прямой можно провести единственную перпендикулярную прямую.

Скрещенные прямые. Секущая

У любых скрещивающихся прямых есть вертикальные углы и смежные.

Если у углов, которые образованы двумя скрещивающимися прямыми, одна сторона общая, то они называются смежными:

Смежные углы в сумме дают 180 градусов.

Если же углы, образованные двумя скрещивающимися прямыми, не имеют общей стороны, то они называются вертикальными:

Вертикальные углы всегда равны.

Если же некоторая прямая пересекает две других прямых, то она называется секущей.

Частным случаем является секущая двух параллельных прямых:

Видео:Параллельные, пересекающиеся и скрещивающиеся прямые | МатематикаСкачать

Взаимное положение прямых

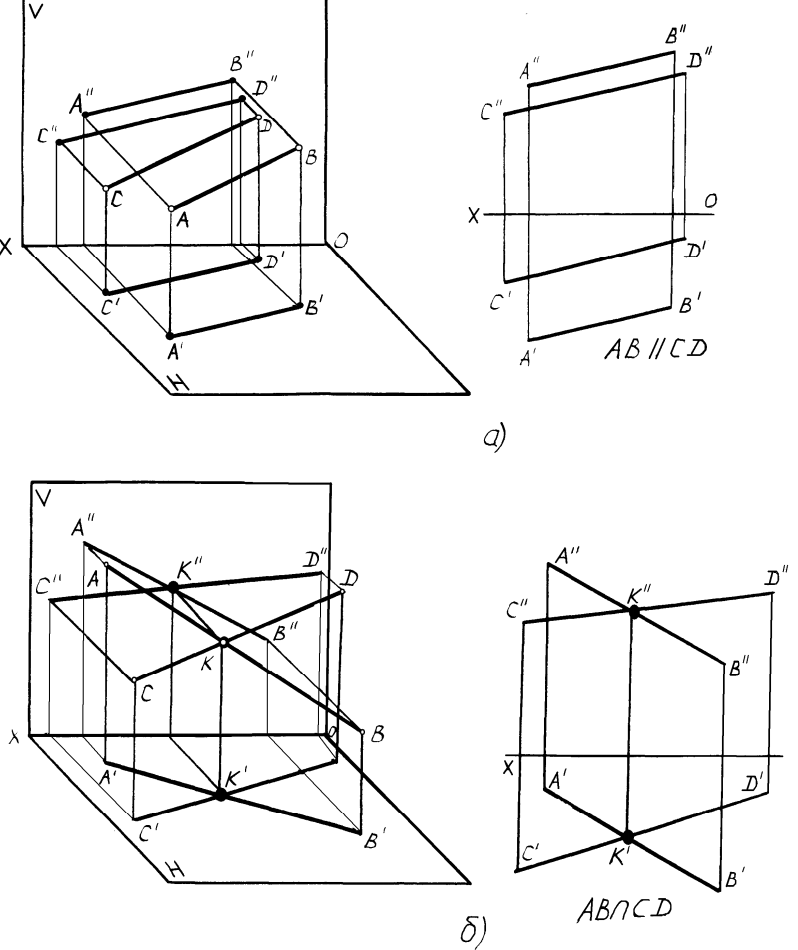
Прямые в пространстве могут быть параллельными, пересекающимися, скрещивающимися и перпендикулярными. Пространственные чертежи и эпюры параллельных и пересекающихся прямых представлены на рисунке 2.7а, б.

Рисунок2.7 – Параллельные и пересекающиеся прямые

Признаком параллельных прямых на эпюре является параллельность

их одноименных проекций.

Пересекающимися прямыми называются прямые, которые имеют

общую точку– точку пересечения. Признаком пересекающихся прямых на

эпюре является то, что проекции точки пересечения находятся на одной

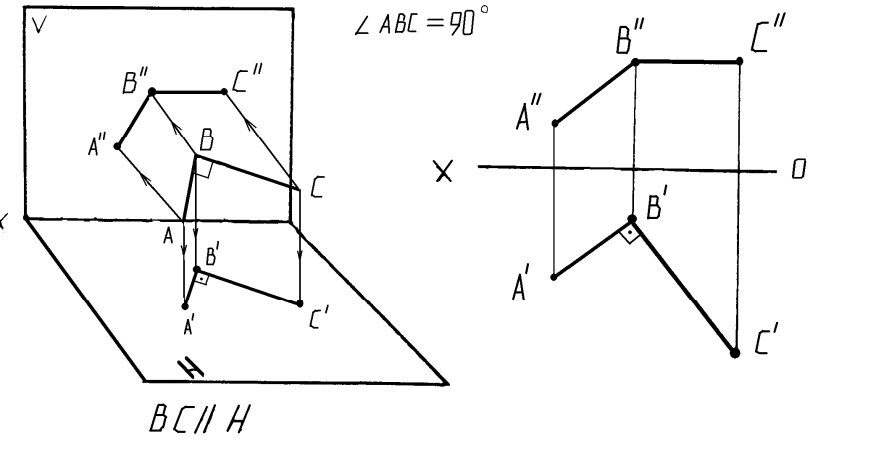
Частным случаем пересекающихся прямых являются

перпендикулярные прямые. В соответствии с теоремой о проецировании

прямого угла, прямой угол будет проецироваться на плоскость проекций в

натуральную величину в том случае, когда одна из его сторон будет

параллельна этой плоскости проекций (Рисунок2.8).

Рисунок2.8 – Перпендикулярные прямые

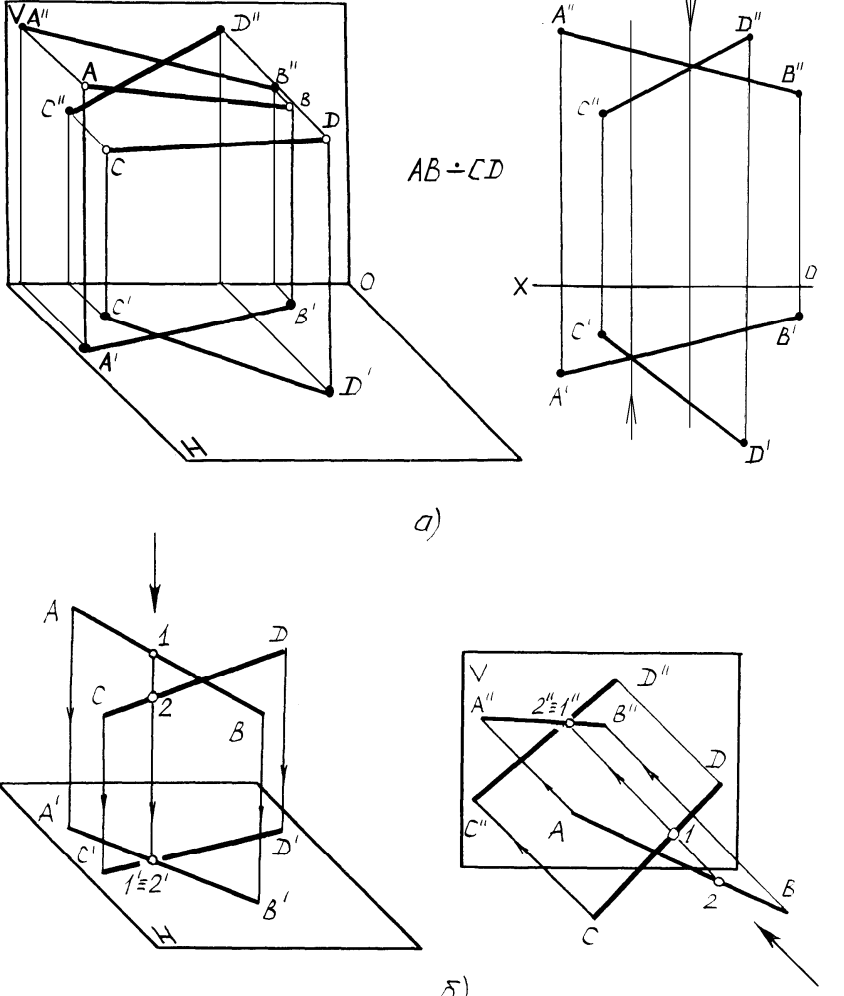
Скрещивающимися прямыми называются непараллельные прямые, не имеющие общей точки. Скрещивающиеся прямые в пространстве не пересекаются, но на эпюре их одноименные проекции накладываются друг на друга, что создает впечатление пересечения.

Признаком скрещивающихся прямых на проекциях является то, что проекции их мнимых точек пересечения не находятся на одной линии связи (рисунок 2.9а). В мнимых точках пересечения конкурируют две точки, принадлежащие разным прямым, или, другими словами, в мнимых точках конкурируют две прямые. Назовем эту область конкурирующим местом. При рассмотрении скрещивающихся прямых возникает вопрос о видимости проекций прямых в конкурирующих местах. Этот вопрос может быть решен методом конкурирующих точек (конкурирующих прямых).

Рисунок2.9 – Скрещивающиеся прямые

Сущность метода заключается в следующем:

1) Отметить конкурирующее место на рассматриваемой проекции;

2) Обозначить конкурирующие точки или записать, какие прямые

3) Провести через конкурирующее место линию связи;

4) Вдоль линии связи сравнить недостающие координаты

конкурирующих точек или конкурирующих прямых;

5) На рассматриваемой проекции будет видна та точка или прямая,

которая имеет наибольшую недостающую координату.

Так на рисунке 2.9б на горизонтальной проекции будет видна точка

1, принадлежащая прямой AB, или, проще говоря, прямая AB, так как

аппликата прямой AB вдоль линии связи наибольшая. На фронтальной

проекции также будет видна прямая AB, так как у неё в конкурирующем

месте наибольшая ордината.

Дата добавления: 2015-11-20 ; просмотров: 1326 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №5. Взаимное расположение прямых в пространстве

Перечень вопросов, рассматриваемых в теме

признаки скрещивающихся прямых;
определение углов с сонаправленными сторонами;
доказательство теоремы о плоскости, проходящей через одну из скрещивающихся прямых;
доказательство теоремы о равенстве углов с сонаправленными сторонами.

Глоссарий по теме

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Два отрезка называются параллельными, если они лежат на паралельных прямых.

Учебник Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия 10-11 кл.– М.: Просвещение, 2014.

Зив Б.Г. Дидактические материалы Геометрия 10 кл.– М.: Просвещение, 2014.
Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь Геометрия 10 кл.-М.: Просвещение, 2013.

Открытый электронный ресурс:

Теоретический материал для самостоятельного изучения

Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)

Рисунок 1 – скрещивающиеся прямые

На прошлом уроке в качестве наглядного примера нами был приведен куб.

Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.

Примеры скрещивающихся прямых вокруг нас:

Одна дорога проходит по эстакаде, а другая под эстакадой

Горизонтальные линии крыши и вертикальные линии стен

Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).

Допустим, что прямые AB и CD всё-таки лежат в одной плоскости.
2. Значит эта плоскость идёт через прямую AB и точку D, то есть она совпадает с плоскостью α.
3. Это противоречит условиям теоремы, что прямая CD не находится в плоскости α, а пересекает её.
Теорема доказана.

Рисунок 2 – скрещивающиеся прямые АВ и СD

Итак, возможны три случая расположения прямых в пространстве:

Разберем и докажем еще одну теорему о скрещивающихся прямых.

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)

1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.

4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Рисунок 3 – прямые АВ, СD, DЕ

Любая прямая, например ОО₁, рассекает плоскость на две полуплоскости. Если лучи ОА и О₁А₁ параллельны и лежат в одной полуплоскости, то они называются сонаправленными.

Лучи О₁А₁ и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)

Рисунок 4 – сонаправленные лучи

Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)

Доказательство:

при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.

Стороны углов сонаправлены, а, значит, параллельны. Проведем через них плоскости- как показано на чертеже.

Отметим на сторонах угла O произвольные точки A и B.

На соответствующих сторонах угла O₁ отложим отрезки OA₁ и O₁B₁ равные соответственно ОA и OB.

2. В плоскости рассмотрим четырехугольник OAA₁O₁.

Так как противолежащие стороны OA и O₁A₁ этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA₁ и OO₁.

3. В плоскости, аналогично можно доказать, что OBB₁O₁ параллелограмм, поэтому равны и параллельны стороны ВВ₁ и OO₁.

4. Если две отрезка AA₁ и BB₁ равны параллельны третьему отрезку OO₁, значит, они равны и параллельны, т. е. АА₁||BB₁ и AA₁ = BB₁.

По определению четырехугольник АВВ₁А₁ – параллелограмм и из этого получаем АВ=А₁В₁.

5.Из выше построенного и доказанного АВ=А₁В₁, ОA =O₁A₁ и OB =O₁B₁ следует, что треугольники AOB и A₁ O₁ B₁. равны по трем сторонам, и поэтому О= О₁.