Как называется точка в которой встречаются все параллельные прямые в изображении (2 видео)

Параллельность прямых

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Содержание

Определение параллельности прямых
Свойства и признаки параллельных прямых
Задача 1
Задача 2
Точка схода параллельных прямых
Новое в блогах
Пересекаются ли параллельные или Что говорил Лобачевский?
📸 Видео

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

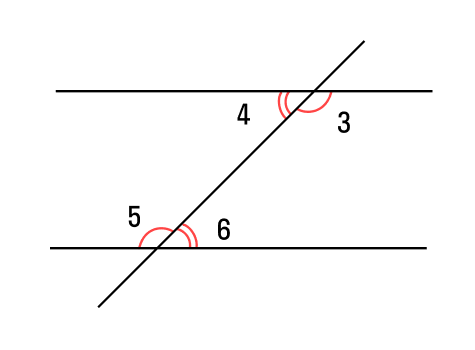
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

два внутренних накрест лежащих угла равны между собой:

два соответственных угла равны между собой:

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Соответственно, ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Точка схода параллельных прямых

Прямая линия, принадлежащая предметной плоскости, имеет точку, беспредельно удаленную от наблюдателя, называемую «предельной точкой прямой». Рассмотрим пример построения перспективы предельной точки прямой линии (рис. 34).

Рис. 34. Перспектива бесконечно удаленной точки: а — на проецирующем аппарате, б — на картинной плоскости А = а

Проведем в предметной плоскости произвольную прямую п’ и построим перспективу двух ее точек А ‘и В’. Получим перспективу отрезка АВ заданной прямой п Продолжим отрезок в обе стороны и получим две точки пересечения: одну — с основанием картины, точку Од, другую — с линией горизонта, точку F. Точка Од — точка, в которой заданная прямая пересекает основание картины, перспектива этой точки совпадает с самой точкой. Далее будем перемещать точку вдоль прямой в предметной плоскости, удаляя ее от картинной плоскости. Тогда перспектива этих точек на картине будет перемещаться вдоль прямой Од F, занимая соответствующие положения. Луч зрения, проведенный в бесконечно удаленную точку заданной прямой, примет направление, параллельное этой прямой, и пересечет картинную плоскость в точке F. Эта точка представляет перспективу бесконечно удаленной точки заданной прямой п’. Прямая Од F не может быть продолжена на картине дальше точки F, так как лучи зрения будут приближаться к положению, параллельному прямой п’. Точка F называется перспективой предельной точки заданной прямой. Отсюда следует, что все параллельные прямые имеют одну общую точку- перспективу предельных точек этих прямых. Она называется точкой схода параллельных прямых. Исключение составляют прямые, расположенные в предметной плоскости параллельно картине: они не имеют картинного следа и точки схода, так как ей параллельны.

Если взять несколько пучков параллельных прямых, принадлежащих предметной плоскости, то для каждого пучка будет своя точка схода. Но все эти точки схода будут расположены на линии горизонта на одинаковой высоте. Высота точек будет соответствовать высоте точки зрения, поскольку лучи зрения, направленные в предельную точку, будут параллельны предметной плоскости (рис. 35). Отсюда следует, что для любой прямой, лежащей в предметной плоскости, перспектива предельной точки отстоит от основания картины на расстояние, равное высоте точки зрения. Совокупность перспектив предельных точек всех прямых, лежащих в предметной плоскости, представляет собой прямую, расположенную параллельно основанию картины и отстоящую от нее на расстояние, равное высоте точки зрения. Эта прямая является линией горизонта и перспективой предельной прямой предметной плоскости. Она ограничивает на картине изображение предметной плоскости со всеми точками и прямыми, ей принадлежащими.

Перспективу предельной точки прямой линии можно построить на проецирующем аппарате следующим образом:

1) провести луч зрения, параллельно заданной прямой линии;
2) построить его проекцию на предметную плоскость;
3) провести плоскость, проецирующую к предметной плоскости, через построенные прямые линии;

Рис.35. Перспектива бесконечно удаленных точек параллельных прямых:

а — на проецирующем аппарате; б — на картинной плоскости

4) найти линию пересечения этой плоскости с картинной плоскостью;

5) найти точку пересечения полученной линии и проецирующего луча, точка F, данная точка и есть перспектива предельной точки прямой линии, расположенной в предметной плоскости.

Используя алгоритм построения предельных точек прямых, построим перспективу угла (рис. 36), образованного двумя пересекающимися прямыми, лежащими в предметной плоскости.

Рис. 36. Перспектива угла:

а — на проецирующем аппарате; б — на картинной плоскости

Перспектива предельной точки параллельных прямых является для них точкой схода. На рис. 37 приведен пример построения точки схода для прямых, расположенных под углом 45° к картинной плоскости. Такими точками являются дистанционные точки.

Дистанционные точки D и D, или точки отдаления, располагаются на линии горизонта слева и справа от точки Р на одинаковом расстоянии, равном

Рис. 37. Перспектива прямой, расположенной под углом 45° к картине: а — на проецирующем аппарате; б- на картинной плоскости расстоянию от точки зрения до картины. Проведем в предметной плоскости прямую т’ под углом 45° к картинной плоскости и построим точку А — перспективу одной из точек (А’) заданной прямой т’. С этой целью в предметной плоскости продолжим прямую т ‘до пересечения с основанием картины в точке Ch. Соединим точку А и точку О2 и продолжим полученную прямую до пересечения с линией горизонта. Прямая О2А пересечет картинную плоскость в точке D. Если перемещать точку Л ‘вдоль прямой в предметной плоскости, удаляя ее от картинной плоскости, то перспективой предельной точки прямой будет являться дистанционная точка D.

Задание. Для закрепления материала постройте самостоятельно перспективу прямой линии, предельной точкой которой будет дистанционная точка D, используя рис. 37.

Восходящая прямая — прямая, которая возвышается над предметной плоскостью по мере ее удаления от картины. Перспектива предельной точки восходящей прямой располагается выше линии горизонта. Построить ее можно следующим образом (рис. 38, 39).

Рис. 38. Перспектива восходящей прямой: а — на проецирующем аппарате; б — на картинной плоскости

Рис. 40. Точка схода

На прямой выделим отрезок А’ и В’ и по-

Рис. 39. Пример перспективы строим его проекцию (отрезок а’Ь’> на предметную плоскость. Теперь находим перспективу предельной точки этой прямой как линии, принадлежащей предметной плоскости (см. рис. 35). Перспективой предельной точкой прямой а’ Ь’ является точка f. Из этой точки строим прямую, перпендикулярную к предметной плоскости, а из точки зрения проводим луч, параллельный заданной восходящей прямой (отрезку А’ и В’). Пересечением этих двух прямых будет точка F, которая и является перспективой предельной точки заданной прямой и точкой схода всех прямых, расположенных параллельно этой прямой.

Нисходящая прямая — прямая, которая снижается над предметной плоскостью по мере ее удаления от картины. Перспектива предельной точки нисходящей прямой располагается ниже линии горизонта.

Задание. Для закрепления материала постройте самостоятельно перспективу отрезка нисходящей прямой линии, используя свойства перспективы.

Для прямых, лежащих перпендикулярно картине, точкой схода будет являться главная точка картины — точка Р, так как она лежит на перпендикуляре, проведенном из точки зрения к картине, а перпендикуляр и есть прямая, параллельная заданному направлению (рис. 40).

Видео:Параллельные прямые. 6 класс.Скачать

Новое в блогах

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Пересекаются ли параллельные или Что говорил Лобачевский?

Недавно в посте на околонаучные темы один из комментаторов завел разговор о геометрии Лобачевского (что он ее не понимает) и даже вроде попросил объяснить. Я тогда ограничилась утверждением, что понимаю. Объяснять эту теорию в ограниченных рамках комментария и одним текстом (без рисунков) показалось мне невозможным.

Однако, подумав, я все же решила попробовать дать небольшой популярный экскурс в эту теорию.

Немного предыстории. Геометрия со времен Евклида стала аксиоматической теорией, в которой большинство утверждений доказывалось на основе нескольких постулатов (аксиом). Считалось, что эти аксиомы «очевидны», т.е. отражают свойства реального (физического) пространства.

Одна из этих аксиом вызывала у ученых подозрение: а нельзя ли ее вывести из остальных постулатов? Современная формулировка этой аксиомы такова:

«Через точку, не лежащую на заданной прямой, можно провести не более одной прямой, параллельной ей». То, что одну-то прямую можно провести, является не аксиомой, а теоремой.

При этом «параллельной» называется прямая, не пересекающая данную. Итак, суть аксиомы в том, что такая прямая – одна!

(Распространенное утверждение «Лобачевский доказал, что параллельные прямые могут и пересекаться» — конечно, является вопиюще неправильным! Ведь это бы противоречило их определению!)

Лобачевский, как и многие до него, решил доказать, что это утверждение можно вывести из других аксиом. Для этого он, как это часто делается в математике, выбрал метод «от противного», т.е. предположил, что прямых, не пересекающих данную, больше одной и попытался вывести из этого противоречие с другими фактами. Но чем дальше он развивал теорию, тем больше убеждался, что никакого противоречия не предвидится! Т.е. получалось, что теория с «неправильным» постулатом тоже имеет право на существование!

Конечно, в первое время его выкладки не признавали, смеялись над ним. Именно поэтому великий Гаусс (который пришел к тем же выводам) не рискнул опубликовать свои результаты. Но со временем пришлось признать, что ЧИСТО ЛОГИЧЕСКИ теория Лобачевского ничем не хуже евклидовой.

Один из остроумных способов убедиться в этом – придумать такие «прямые», которые ведут себя как «прямые» Лобачевского. И математики нашли такой пример, и не один.

Пожалуй, самой простой является модель Пуанкаре. Вы можете сами построить ее нехитрыми приборами.

Начертите не листке бумаги прямую. Возьмите циркуль и, ставя его иглу на эту прямую, нарисуйте полуокружности, находящиеся с одной стороны от прямой. Теперь сотрите прямую (и с ней – концевые точки полуокружностей). Так вот, эти полуокружности «без концов» и будут вести себя, как прямые в геометрии Лобачевского!

Действительно, выделим одну полуокружность и точку вне нее. Есть достаточно много полуокружностей, которые не пересекаются с исходной и все проходят через данную точку. Среди них выделяются две: они касаются нашей исходной «прямой» в концевых точках (которые мы, как Вы помните, стерли) Т.е. реального пересечения не происходит. Эти две окружности задают «границы», между которыми находятся все прямые, не пересекающие данную. Их – бесконечное количество.

Можно заметить, что треугольники в этой модели не такие, как на плоскости (евклидовой): сумма их углов меньше 180 градусов! Впрочем, чем меньше треугольник, тем больше сумма его углов. В «малом», на небольших расстояниях, геометрия Лобачевского практически совпадает с геометрией Евклида. Поэтому, вообще говоря, мы не сможем «экспериментально» отличить одну от другой, если окажется, что доступные нам (космические) расстояния– малы для этой цели.

Впрочем, в наше время ни физики, ни, тем более, математики, не пытаются воспринимать геометрию Лобачевского как модель «реального», физического пространства. Математики поняли, что все, что они могут сказать: если верны такие-то аксиомы, то верны и такие-то теоремы. Ну, а что такое «множества», «точки», «прямые», «углы», «расстояния», и т.п. – этого мы не знаем! Прямо как у Станислава Лема: «Сепульки – это объекты для сепулькирования»

«Говорят, Бертран Рассел определил математику как науку, в которой мы никогда не знаем, о чем говорим, и насколько правильно то, что мы говорим. Известно, что математика широко применяется во многих других областях науки. [ … ] Таким образом, одна из главных функций математического доказательства – создание надежной основы для проникновения в суть вещей.»