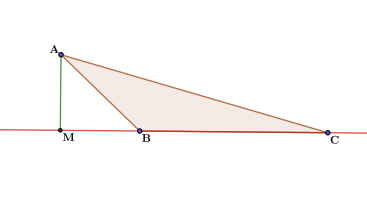
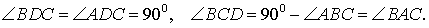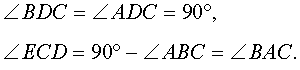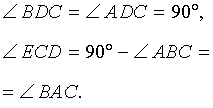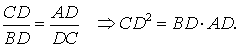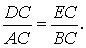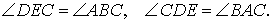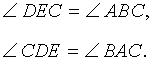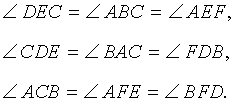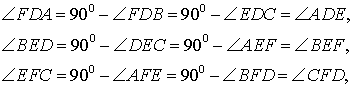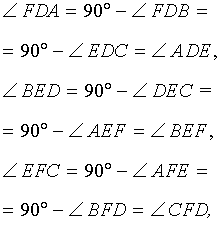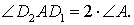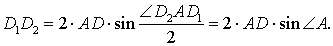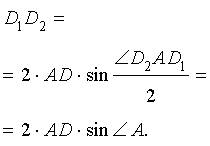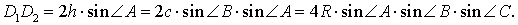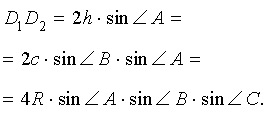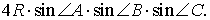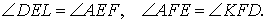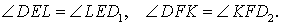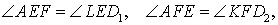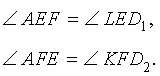В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.
- Определение вершины треугольника
- Характеристики понятия
- Использование вершины треугольника
- Что мы узнали?
- Треугольник. Формулы определения и свойства треугольников.
- Определение треугольника
- Классификация треугольников
- 1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
- 2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
- 3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
- 4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
- 5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
- 6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
- Свойства треугольника
- 1.Свойства углов и сторон треугольника.
- 2.Теорема синусов.
- 3. Теорема косинусов.
- 4. Теорема о проекциях
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Как найти вершины тупоугольного треугольника
- Высота треугольника. Свойство высоты прямоугольного треугольника
- Расположение высот у треугольников различных типов
- Ортоцентр треугольника
- Расположение ортоцентров у треугольников различных типов
- Ортоцентрический треугольник
- Задача Фаньяно
- Определения
- Пример решения задачи
- Что мы узнали?
- Тест по теме
- Оценка статьи
- Содержание
- Бонус
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Определение вершины треугольника
В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.
Рис. 1. Вершина в треугольнике.
Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.
Рис. 2. Обозначение вершин в треугольнике.
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Характеристики понятия
Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).
Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.
Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.
Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Использование вершины треугольника
При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.
Рис. 3. Свойство внешнего угла треугольника.
Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.
Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Что мы узнали?
Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.
Видео:Построение высоты в треугольникеСкачать

Треугольник. Формулы определения и свойства треугольников.
В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
Видео:Уравнения стороны треугольника и медианыСкачать

Определение треугольника
Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Треугольник ABC (△ABC)
- Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.
Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:
Видео:Вычисляем высоту через координаты вершин 1Скачать

Классификация треугольников
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Свойства треугольника
1.Свойства углов и сторон треугольника.
- Сумма всех углов треугольника равна 180°:
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема о проекциях
Для остроугольного треугольника:
Видео:немногие знают, как резать уголки для соединений под углом 90 градусов с точными результатами.Скачать

Медианы треугольника
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
5. Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны:
Видео:Высоты треугольника.Скачать

Как найти вершины тупоугольного треугольника
 Высота треугольника. Свойство высоты прямоугольного треугольника Высота треугольника. Свойство высоты прямоугольного треугольника |
 Расположение высот у треугольников различных типов Расположение высот у треугольников различных типов |
 Ортоцентр треугольника Ортоцентр треугольника |
 Расположение ортоцентров у треугольников различных типов Расположение ортоцентров у треугольников различных типов |
 Ортоцентрический треугольник Ортоцентрический треугольник |
 Задача Фаньяно Задача Фаньяно |
Видео:Медиана, высота и биссектриса треугольника. Центроид, инцентр, ортоцентр. Геометрия 7 класс.Скачать

Высота треугольника. Свойство высоты прямоугольного треугольника
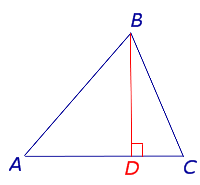
Определение 1 . Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).
На рисунке 1 изображена высота BD , проведённая из вершины B треугольника ABC . Точка D – основание высоты.
Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.
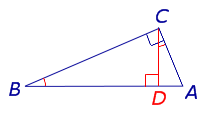
Утверждение . Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).
Доказательство . Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям
Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD , что и требовалось доказать.
Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.
Видео:Построение медианы в треугольникеСкачать

Расположение высот у треугольников различных типов
| Фигура | Рисунок | Описание |
| Остроугольный треугольник | 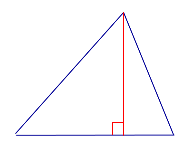 | Все высоты остроугольного треугольника лежат внутри треугольника. |
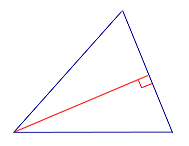 | ||
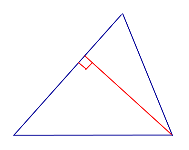 | ||
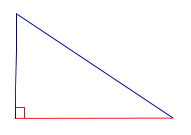
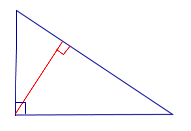
| Прямоугольный треугольник | 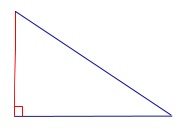 | Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника |
 | ||
 | ||
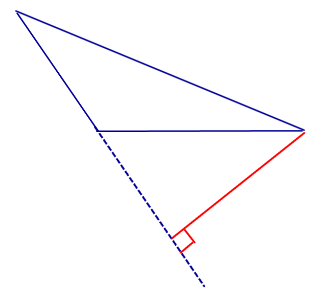
| Тупоугольный треугольник | 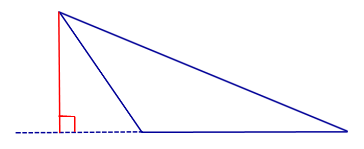 | Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
 | ||
 |
| Остроугольный треугольник | ||
 |  |  |
| Все высоты остроугольного треугольника лежат внутри треугольника. | ||
| Прямоугольный треугольник | ||
 |  |  |
| Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника | ||
| Тупоугольный треугольник | ||
 |  |  |
| Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника | ||
Все высоты остроугольного треугольника лежат внутри треугольника.
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника
Видео:Нахождение длины отрезка по координатамСкачать

Ортоцентр треугольника
Теорема 1 . Высоты треугольника (или их продолжения) пересекаются в одной точке.
Доказательство . Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).
Обозначим точки пересечения этих прямых символами A1 , B1 и C1 , как показано на рисунке 3.
Следовательно, точка B является серединой стороны C1A1 .
Следовательно, точка A является серединой стороны C1B1 .
Следовательно, точка C является серединой стороны B1A1 .
и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.
Теорема 1 доказана.
Определение 2 . Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.
У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.
Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Расположение ортоцентров у треугольников различных типов
| Фигура | Рисунок | Описание |
| Остроугольный треугольник | 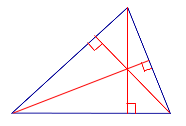 |
Ортоцентр остроугольного треугольника лежит внутри треугольника.
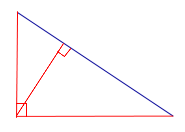
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
Ортоцентр тупоугольного треугольника лежит вне треугольника.
В ортоцентре тупоугольного треугольника пересекаются не высоты, а продолжения высот треугольника.
Ортоцентр остроугольного треугольника лежит внутри треугольника.
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
Ортоцентр тупоугольного треугольника лежит вне треугольника.
В ортоцентре тупоугольного треугольника пересекаются не высоты, а продолжения высот треугольника.
Видео:Установка наслонных стропил в одиночку. Разметка стропил по месту.Скачать

Ортоцентрический треугольник
Решим следующую задачу.
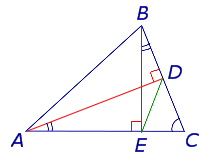
Задача . В остроугольном треугольнике ABC проведены высоты AD и BE (рис.5). Доказать, что треугольник DCE подобен треугольнику ABC .
Решение . Рассмотрим треугольники ADC и BEC . Эти треугольники подобны в силу признака подобия прямоугольных треугольников с равными острыми углами (угол C общий). Следовательно, справедливо равенство
Это равенство, а также наличие общего угла C позволяют на основании признака подобия треугольников заключить, что и треугольники DCE и ABC подобны. Решение задачи завершено.
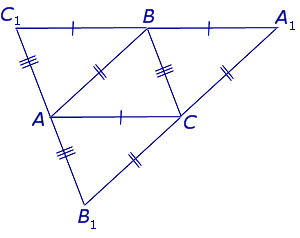
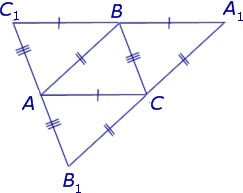
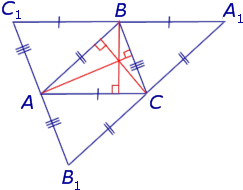
Определение 3 . Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника (рис 6).
Из определения 3 и следствия 1 вытекает следствие 2.
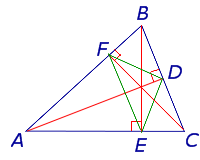
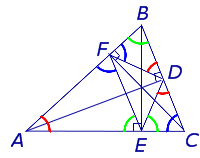
Следствие 2 . Пусть FDE – ортоцентрический треугольник с вершинами в основаниях высот остроугольного треугольника ABC (рис 7).
Тогда справедливы равенства
Из следствия 2 вытекает теорема 2.
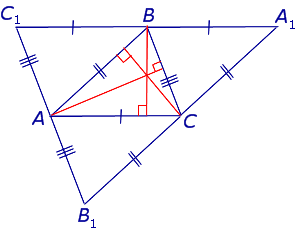
Теорема 2 . Высоты остроугольного треугольника являются биссектрисами углов его ортоцентрического треугольника (рис.7).
Доказательство . Воспользовавшись следствием 2, получаем:
что и требовалось доказать.
Видео:Вершины треугольникаСкачать
Задача Фаньяно
Задача Фаньяно . Рассматриваются всевозможные треугольники DEF , вершины D, E и F которых лежат на сторонах BC, AC и AB остроугольного треугольника ABC соответственно. Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника ABC .
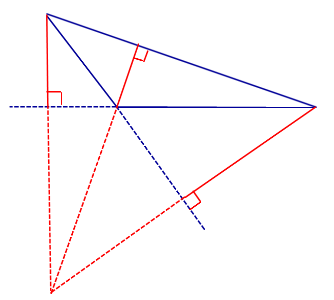
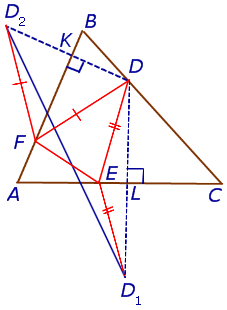
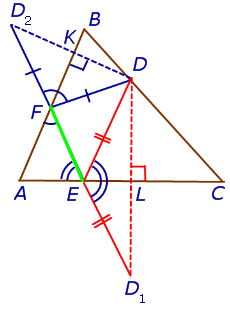
Решение . Пусть DEF – один из рассматриваемых треугольников. Обозначим символом D1 точку, симметричную точке D относительно прямой AC , и обозначим символом D2 точку, симметричную точке D относительно прямой AB (рис.8).
Поскольку отрезок прямой – кратчайшее расстояние между двумя точками, то периметр треугольника DEF оказывается не меньшим, чем длина отрезка D1D2 . Отсюда вытекает, что при фиксированной точке D наименьшим периметром обладает такой треугольник DEF , вершины F и E которого являются точками пересечения прямой D1D2 с прямыми AB и AC соответственно. Периметр этого треугольника равен длине отрезка D1D2 (рис.9).
Заметим также, что выполнено равенство
Кроме того, выполнено равенство
Отсюда вытекает, что длина отрезка D1D2 будет наименьшей тогда, когда длина отрезка AD будет наименьшей, т.е. в том случае, когда отрезок AD является высотой треугольника ABC . Другими словами, наименьшим периметром обладает такой треугольник DEF , у которого вершина D является основанием высоты треугольника ABC , проведённой из вершины A , а вершины E и F построены по описанной выше схеме. Таким образом, среди всевозможных треугольников DEF треугольник с наименьшим периметром является единственным.
Если обозначить длину высоты, проведённой из вершины A , длину стороны AB и радиус описанной около треугольника ABC окружности буквами h, c и R соответственно, то, воспользовавшись теоремой синусов, получим:
Следовательно, наименьший периметр рассматриваемых треугольников DEF равен
Теперь докажем, что ортоцентрический треугольник и является треугольником с наименьшим периметром. Для этого воспользуемся следующей леммой.
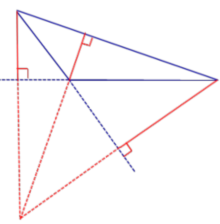
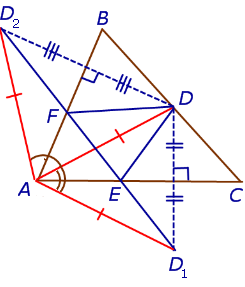
Лемма . Пусть DEF – ортоцентрический треугольник треугольника ABC (рис.10).
В этом случае отрезок D1D2 проходит через точки F и E .
Доказательство . Заметим, что в силу следствия 2 выполняются равенства:
Кроме того, в силу равенства треугольников DFK и KFD2 , а также в силу равенства треугольников DEL и LED1 выполняются равенства:
откуда вытекает, что углы AEF и D1EL , а также AFE и D2FK являются вертикальными углами. Это означает, что точки D1 , F, E , D2 лежат на одной прямой. Лемма доказана.
Доказательство леммы и завершает решение задачи Фаньяно.
Рассмотрим, как построить высоту треугольника с помощью чертежного угольника.
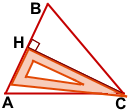
Чтобы построить высоту остроугольного треугольника, надо приложить угольник так, чтобы одна сторона прямого угла проходила через вершину треугольника, а вторая — через противоположную этой вершине сторону.
AK — высота треугольника ABC, проведённая из вершины A к противолежащей стороне BC.
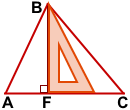
BF — высота треугольника ABC, опущенная из вершины B на сторону AC.
CH — высота треугольника ABC, проведённая из вершины C к стороне AB.
Все высоты треугольника пересекаются в одной точке.
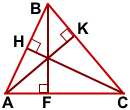
Если требуется построить все высоты треугольника, достаточно построить две, а третью провести из вершины треугольника через точку пересечения двух высот.
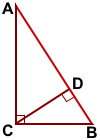
В прямоугольном треугольнике две стороны (катеты) являются также его высотами. Остаётся построить третью высоту.
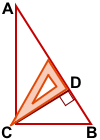
CD — высота прямоугольного треугольника ABC, проведённая из вершины прямого угла C к гипотенузе AB.
Точка пересечения высот прямоугольного треугольника — вершина прямого угла.
Высоты AC, BC и CD прямоугольного треугольника ABC пересекаются в точке C, ∠C=90°.
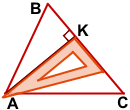
В тупоугольном треугольнике проще всего построить высоту, выходящую из вершины тупого угла.
Прикладываем угольник прямым углом так, чтобы одна его сторона проходила через наибольшую сторону треугольника, а другая — через тупой угол.
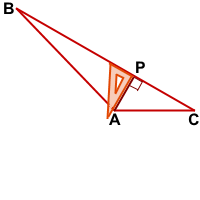
AP — высота тупоугольного треугольника ABC, проведённая из вершины тупого угла A к стороне BC.
Только высота, проведённая из вершины тупого угла, лежит внутри треугольника. Две другие высоты находятся вне него.
Высоты тупоугольного треугольника, выходящие из вершин острых углов, проведены не к противолежащим сторонам, а к прямым, содержащим эти стороны.
Чтобы построить высоту, продлеваем противолежащую сторону и прикладываем угольник прямым углом таким образом, чтобы одна сторона угольника проходила через построенную прямую, а другая — через вершину острого угла.
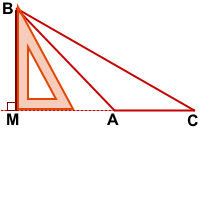
BM — высота тупоугольного треугольника ABC, проведённая из вершины острого угла B к прямой, содержащей противолежащую сторону AC.
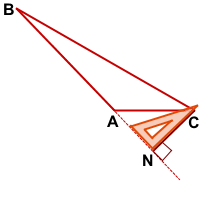
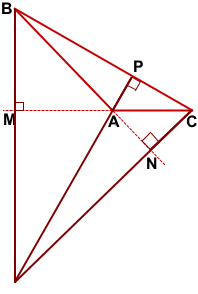
CN — высота тупоугольного треугольника ABC, проведённая из вершины острого угла С к прямой, содержащей противолежащую сторону AB.
Точка пересечения высот тупоугольного треугольника лежит вне него, за тупым углом, напротив наибольшей стороны.
Чтобы построить точку пересечения высот треугольника ABC, продлим прямые BM, CN и AP до пересечения.
Мы рассмотрели, как строить высоты треугольника с помощью угольника.
Построение высот с помощью циркуля и линейки будем рассматривать в теме «Задачи на построение».
Видео:Вычисляем угол через координаты вершинСкачать

Определения
Тупоугольным треугольником будет называться любой треугольник, содержащий тупой угол. Тупоугольный треугольник может быть равнобедренным, но при этом не может быть равносторонним или прямоугольным. Собственно на этом свойства этой фигуры заканчиваются. В остальном это обычный треугольник и подход к решению таких фигур ничем не отличается.
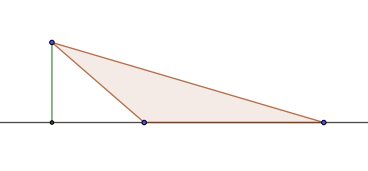
Рис. 1. Тупоугольный треугольник.
В треугольнике сумма углов равна 180 градусам, поэтому только один угол треугольника может быть тупым, два других при этом всегда острые. Площадь тупоугольного треугольника находится так же, как площадь произвольного треугольника.
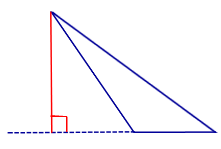
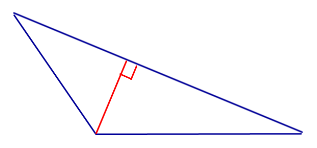
Рис. 2. Высота в тупоугольном треугольнике.
Только в тупоугольном треугольнике высота может лежать за пределами треугольника.
Рассмотрим несколько интересных задач на нахождение данных в тупоугольном треугольнике.
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Пример решения задачи
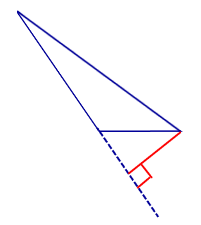
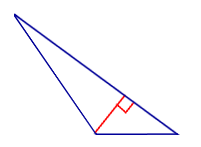
Рис. 3. Рисунок к задаче.
Для решения любой задачи можно найти несколько способов. В данной ситуации можно пойти через площадь треугольников, достроить тупоугольный треугольник до прямоугольного или воспользоваться теоремой косинусов. Каждый из способов дает представление о том, как можно решать задачи с тупоугольным треугольником. Воспользуемся каждым из них.
Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.
- Через площадь треугольников. Площадь можно найти как половину произведения основания на высоту, проведенную к этому основанию. А можно как половину произведения двух сторон на синус угла между ними. Нам известен косинус угла, а через косинус всегда можно найти синус.
Теперь запишем две формулы площади, выразим через них высоту и найдем ее значение.
- Второй способ это достроить тупоугольный треугольник до прямоугольного. Если присмотреться, то можно заметить на чертеже два прямоугольных треугольника – это треугольники АМС и АМВ. В треугольнике АМВ можно найти косинус угла АВМ с помощью формул-приведений. Затем через значение косинуса найти значение синуса того же угла. А синус это отношение противолежащего катета к гипотенузе. Противолежащей катет – это искомая нами высота, а гипотенуза это сторона АВ прямоугольного треугольника.
Тогда синус, как и в первом способе, выразим через основное тригонометрическое тождество.
- Третий метод это теорема синусов и косинусов. Для того, чтобы воспользоваться этим способом, через теорему косинусов найдем значение АС, потом через теорему синусов найдем синус угла АСВ и определим АМ из синуса угла АСВ большого прямоугольного треугольника АМС.
$$sqrt =sqrt =sqrt =3sqrt $$ – по теореме косинусов.
Значение синуса угла АВС определим по основному тригонометрическому тождеству.
Выразим искомый синус угла АСВ.
Выразим из треугольника АМС и найденного значения синуса сторону АМ.
Ответы всех трех способов совпали, а значит задача решена верно.
Видео:№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

Что мы узнали?
Мы поговорили об определении тупоугольного треугольника. Узнали и посмотрели на практике, какие методы решения тупоугольных треугольников существуют, а так же выяснили ,какие формулы и теоремы необходимо знать для успешного решения тупоугольного треугольника.
Видео:Скрытые возможности обычного угольника! А вы их знали?Скачать

Тест по теме
Оценка статьи
Средняя оценка: 4.6 . Всего получено оценок: 134.
Не понравилось? — Напиши в комментариях, чего не хватает.
Содержание
- Определения
- Пример решения задачи
- Что мы узнали?
Бонус
- Тест по теме
- Площадь прямоугольного треугольника
- Высота треугольника
- Площадь правильного треугольника
- Площадь прямого треугольника
- Площадь равностороннего треугольника
- Площадь равнобедренного треугольника
- Медиана треугольника
- Правильный треугольник Тупоугольный треугольник
- Остроугольный треугольник
- Свойства прямоугольного треугольника
- Стороны прямоугольного треугольника
- Средняя линия прямоугольного треугольника
- Признаки подобия прямоугольных треугольников
- Высота равностороннего треугольника
- Медиана равностороннего треугольника
- Неравенство треугольника
- Длина медианы правильного треугольника
- Равнобедренный тупоугольный треугольник
- Средняя линия прямоугольного треугольника
- Длина средней линии треугольника
По многочисленным просьбам теперь можно: сохранять все свои результаты, получать баллы и участвовать в общем рейтинге.
- 1.
Михаил Тяпин 214
- 2.
Наталия Дробот 198
- 3.
Мария Кауфман 192
- 4.
Игорь Проскуренко 157
- 5.
Соня Зверева 153
- 6.
Василиса Варавкина 119
- 7.
Иоанн Стефановский 107
- 8.
Софья Холена 94
- 9.
Оля Проскурина 85
- 10.
Татьяна Бежина 83
- 1.
Мария Николаевна 13,500
- 2.
Лариса Самодурова 12,695
- 3.
Liza 12,310
- 4.
Кристина Волосочева 11,445
- 5.
TorkMen 11,441
- 6.
Ekaterina 11,176
- 7.
Влад Лубенков 11,100
- 8.
Лиса 11,070
- 9.
Юлия Бронникова 11,060
- 10.
Вячеслав 10,840
Самые активные участники недели:
- 1. Виктория Нойманн — подарочная карта книжного магазина на 500 рублей.
- 2. Bulat Sadykov — подарочная карта книжного магазина на 500 рублей.
- 3. Дарья Волкова — подарочная карта книжного магазина на 500 рублей.
Три счастливчика, которые прошли хотя бы 1 тест:
- 1. Наталья Старостина — подарочная карта книжного магазина на 500 рублей.
- 2. Николай З — подарочная карта книжного магазина на 500 рублей.
- 3. Давид Мельников — подарочная карта книжного магазина на 500 рублей.
Карты электронные(код), они будут отправлены в ближайшие дни сообщением Вконтакте или электронным письмом.