Mathcad содержит функции для обычных в линейной алгебре действий с массивами. Эти функции предназначены для использования с векторами и матрицами. Если явно не указано, что функция определена для векторного или матричного аргумента, не следует в ней использовать массивы как аргумент. Обратите внимание, что операторы, которые ожидают в качестве аргумента вектор, всегда ожидают вектор-столбец, а не вектор-строку. Чтобы заменить вектор-строку на вектор-столбец, используйте оператор транспонирования [Ctrl]1.
Если Вы используете Mathcad PLUS, Вы будете также иметь несколько дополнительных функций, определенных для векторов. Эти функции скорее предназначены для анализа данных, чем для действий с матрицами. Они обсуждены в Главе “Встроенные функции”.
Следующие таблицы перечисляют векторные и матричные функции Mathcad. В этих таблицах
- A и B — массивы (векторы или матрицы).
- v — вектор.
- M и N — квадратные матрицы.
- z — скалярное выражение.
- Имена, начинающиеся с букв m, n, i или j — целые числа.
Размеры и диапазон значений массива
В Mathcad есть несколько функций, которые возвращают информацию относительно размеров массива и диапазона его элементов. Рисунок 10 показывает, как эти функции используются.
| Имя функции | Возвращается. |
| rows(A) | Число строк в массиве A. Если А — скаляр, возвращается 0. |
| cols(A) | Число столбцов в массиве A. Если A скаляр, возвращается 0. |
| length(v) | Число элементов в векторе v. |
| last(v) | Индекс последнего элемента в векторе v. |
| max(A) | Самый большой элемент в массиве A. Если A имеет комплексные элементы, возвращает наибольшую вещественную часть плюс i, умноженную на наибольшую мнимую часть. |
| min(A) | Самый маленький элемент в массиве A. Если A имеет комплексные элементы, возвращает наименьшую вещественную часть плюс i, умноженную на наименьшую мнимую часть. |
Рисунок 10: Векторные и матричные функции для нахождения размера массива и получения информации относительно диапазона элементов.
Специальные типы матриц
Можно использовать следующие функции, чтобы произвести от массива или скаляра матрицу специального типа или формы. Функции rref, diag и geninv доступны только в Mathcad PLUS.
| Имя функции | Возвращается. |
| identity(n) | n x n единичная матрица (матрица, все диагональные элементы которой равны 1, а все остальные элементы равны 0). |
| Re(A) | Массив, состоящий из элементов, которые являются вещественными частями элементов A. |
| Im(A) | Массив, состоящий из элементов, которые являются мнимыми частями элементов A. |
| Е diag(v) | Диагональная матрица, содержащая на диагонали элементы v. |
| Е geninv(A) | Левая обратная к A матрица L такая, что L A = I, где I — единичная матрица, имеющая то же самое число столбцов, что и A. Матрица А — m x n вещественная матрица, где m>=n. A = I, где I — единичная матрица, имеющая то же самое число столбцов, что и A. Матрица А — m x n вещественная матрица, где m>=n. |
| Е rref(A) | Ступенчатая форма матрицы A. |
Рисунок 11: Функции для преобразования массивов. Обратите внимание, что функции diag и rref являются доступными только в Mathcad PLUS.
Специальные характеристики матрицы
Можно использовать функции из следующей таблицы, чтобы найти след, ранг, нормы и числа обусловленности матрицы. Кроме tr, все эти функции доступны только в Mathcad PLUS.
| Имя функции | Возвращается. |
| tr(M) | Сумма диагональных элементов, называемая следом M. |
| Е rank(A) | Ранг вещественной матрицы A. |
| Е norm1(M) | L1 норма матрицы M. |
| Е norm2(M) | L2 норма матрицы M. |
| Е norme(M) | Евклидова норма матрицы M. |
| Е normi(M) | Равномерная норма матрицы M. |
| Е cond1(M) | Число обусловленности матрицы M, основанное на L1 норме. |
| Е cond2(M) | Число обусловленности матрицы M, основанное на L2 норме. |
| Е conde(M) | Число обусловленности матрицы M, основанное на евклидовой норме. |
| Е condi (M) | Число обусловленности матрицы M, основанное на равномерной норме. |
Формирование новых матриц из существующих
В Mathcad есть две функции для объединения матриц вместе — бок о бок, или одна над другой. В Mathcad также есть функция для извлечения подматрицы. Рисунки 12 и 13 показывают некоторые примеры.
| Имя функции | Возвращается. |
| augment (A, B) | Массив, сформированный расположением A и B бок о бок. Массивы A и B должны иметь одинаковое число строк. |
| stack (A, B) | Массив, сформированный расположением A над B. Массивы A и B должны иметь одинаковое число столбцов. |
| submatrix (A, ir, jr, ic, jc) | Субматрица, состоящая из всех элементов, содержащихся в строках с ir по jc и столбцах с ic по jc. Чтобы поддерживать порядок строк и-или столбцов, удостоверьтесь, что ir |
Рисунок 12: Объединение матриц функциями stack и augment.
Рисунок 13: Извлечение субматрицы из матрицы при помощи функции submatrix.
Собственные значения и собственные векторы
В Mathcad существуют функции eigenval и eigenvec для нахождения собственных значений и собственных векторов матрицы. В Mathcad PLUS также есть функция eigenvecs для получения всех собственных векторов сразу. Если Вы используете Mathcad PLUS, Вы будете также иметь доступ к genvals и genvecs для нахождения обобщенных собственных значений и собственных векторов. Рисунок 14 показывает, как некоторые из этих функций используются.
| Имя функции | |
| eigenvals (M) | Вектор, содержащий собственные значения матрицы M. |
| eigenvec (M, z) | Матрица, содержащая нормированный собственный вектор, соответствующий собственному значению z квадратной матрицы M. |
| Е eigenvecs (M) | Матрица, содержащая нормированные собственные векторы, соответствующие собственным значениям квадратной матрицы M. n-ный столбец возвращенной матрицы — собственный вектор, соответствующий n-ному собственному значению, возвращенному eigenvals. |
| Е genvals (M,N) | Вектор v собственных значений, каждое из которых удовлетворяет обобщенной задаче о собственных значениях . Матрицы M и N — вещественнозначные квадратные матрицы одного размера. Вектор x — соответствующий собственный вектор. |
| Е genvecs (M,N) | Матрица, содержащая нормализованные собственные векторы, соответствующие собственным значениям в v, векторе, возвращенном genvals. n-ный столбец этой матрицы — собственный вектор x, удовлетворяющий обобщенной задаче о собственных значениях . Матрицы M и N — вещественнозначные квадратные матрицы одного размера. |
Рисунок 14: Нахождение собственных значений и собственных векторов.
Рисунок 15: Использование eigenvecs для одновременного нахождения всех собственных векторов.
Если Вы используете Mathcad PLUS, Вы будете иметь доступ к некоторым дополнительным функциям для выполнения специальных разложений матрицы: QR, LU, Холесского, и по сингулярным базисам. Некоторые из этих функций возвращают две или три матрицы, соединенные вместе в одну большую матрицу. Используйте submatrix, чтобы извлечь эти две или три меньшие матрицы. Рисунок 16 показывает пример.
| Имя функции | Возвращается. |
| Е cholesky(M) | Нижняя треугольная матрица L такая, что L L T =M. Матрица M должна быть симметричной положительно определенной. Симметрия означает, что M=M T , положительная определённость — что x T L T =M. Матрица M должна быть симметричной положительно определенной. Симметрия означает, что M=M T , положительная определённость — что x T  M M x>0 для любого вектора x x>0 для любого вектора x  0. 0. |
| Е qr(A) | Матрица, чьи первые n столбцов содержат ортогональную матрицу Q, а последующие столбцы содержат верхнюю треугольную матрицу R. Матрицы Q и R удовлетворяют равенству A=Q R. Матрица A должна быть вещественной. R. Матрица A должна быть вещественной. |
| Е lu(M) | Матрица, которая содержит три квадратные матрицы P, L и U, расположенные последовательно в указанном порядке и имеющие с M одинаковый размер. L и U являются соответственно нижней и верхней треугольными матрицами. Эти три матрицы удовлетворяют равенству P M=L M=L U . U . |
| Е svd(A) | Матрица, содержащая две расположенные друг над другом матрицы U и V. Сверху находится U — размера m x n, снизу V — размера n x n. Матрицы U и V удовлетворяют равенству A=U diag(s) diag(s) V T , где s — вектор, возвращенный svds(A). A должна быть вещественнозначной матрицей размера m x n, где m>=n. V T , где s — вектор, возвращенный svds(A). A должна быть вещественнозначной матрицей размера m x n, где m>=n. |
| Е svds(A) | Вектор, содержащий сингулярные значения вещественнозначной матрицы размера m x n, где m>=n. |
Рисунок 16: Использование функции submatrix для извлечения результата из функции rq. Используйте submatrix, чтобы извлечь подобным образом результаты из функций lu и svd. Обратите внимание, что эти функции доступны только в Mathcad PLUS.
Решение линейной системы уравнений
Если Вы используете Mathcad PLUS, Вы сможете использовать функцию lsolve для решения линейной системы уравнений. Рисунок 17 показывает пример. Обратите внимание, что M не может быть ни вырожденной, ни почти вырожденной для использования с lsolve. Матрица называется вырожденной, если её детерминант равен нулю. Матрица почти вырождена, если у неё большое число обусловленности. Можно использовать одну из функций, описанных на странице 204, чтобы найти число обусловленности матрицы.
| Имя функции | |
| Е lsolve (M, v) | Вектор решения x такой, что M x=v. x=v. |
Если Вы не используете Mathcad PLUS, Вы всё-таки можете решать систему линейных уравнений, используя обращение матрицы, как показано в нижнем правом углу Рисунка 9.
Рисунок 17: Использование lsolve для решения системы из двух уравнений с двумя неизвестными.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Видео:Угол между векторами | МатематикаСкачать

Тригонометрические функции (Trigonometric)
Аргумент тригонометрических функций и результат обратных тригонометрических функций выражаются в радианах. Чтобы использовать значение угла в градусах, его необходимо перевести в радианы (листинг 10.6). Аргумент тригонометрических функций может быть комплексным.
Листинг 10.4. Примеры тригонометрических функций
Листинг 10.5. Примеры расчета угла между прямой и осью OX
Листинг 10.6. Расчет тригонометрических функций в градусах
1. Электромагнитная волна (в религиозной терминологии релятивизма — «свет») имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например,
200 тыс км/с в стекле и
3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью «Температура эфира и красные смещения»), разную скорость для разных частот (см. статью «О скорости ЭМ-волн»)
2. В релятивизме «свет» есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский «свет» — это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те «подтверждающие теорию Эйнштейна факты», которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
Видео:Угол между векторами. 9 класс.Скачать

Осваиваем Mathcad (стр. 5 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 |
Правильность расчетов подтверждается просмотром столбцов матрицы PointABCE.
Эти расчеты позволяют уточнить диапазон переменных для вывода плоскости PABC на чертеж:
Полностью аналогично определяем диапазон переменных для вывода плоскости PD.
Выводим чертеж и показываем невидимые ребра пунктиром (щелчком по графику вызываем окно форматирования графика, выбираем вкладку Special и для невидимых ребер указываем Line Style (стиль линий) Dashed (пунктир). Этой операцией заканчивается построение чертежа. Получится так (рис. 2.62):
Этап 7 завершен.
Задания 1,2 выполнены.
Из курса алгебры мы знаем, что длина вектора определяется как корень квадратный из суммы квадратов разностей координат начала и конца вектора:
Средства Mathcad позволяют такие вычисления делать быстрее, с помощью встроенной функции «длина вектора», которая обозначается вертикальными линиями. Формируем разность векторов координат точек A и B и вычисляем длину:
Длина ребра GH находится аналогично.
8.2.3. Пояснения к заданию 4 «Найти угол между ребрами AB и AC, сделать проверку».
· Этап 1. Формируем векторы AB и AC, используя найденные выше координаты вершин A, B, C.
· Этап 2. Пользуясь встроенной процедурой Mathcad или формулой, изученной в курсе алгебры, находим скалярное произведение векторов AB и AC по значениям проекций этих векторов на оси.
· Этап 3. Сопоставляем результат этапа 2 с иной формулой скалярного произведения (произведение длин векторов на косинус угла между ними). Приравнивая два варианта формул скалярного произведения друг к другу, находим угол между векторами.
· Этап 4. Для проверки находим угол между векторами BA и BE, см. чертеж к этапу 7 заданий 1, 2. Для параллелограмма сумма углов между векторами (AB, AC) и (BA, BE) должна составить p радиан (180°).
Выполнение этапа 1 «Формирование векторов AB и AC». Используя формулы алгебры, рассчитываем проекции векторов на оси по разности координат точек на их границах:
Этап 1 завершен.
Выполнение этапа 2 «Расчет скалярного произведения векторов AB и AC». Формула для расчета скалярного произведения ScalarAB_AC, известная из курса алгебры:
В Mathcad имеется встроенная функция, позволяющая найти скалярное произведение быстрее, используя транспонирование одного из векторов (любого) ( + ):
Этап 2 завершен.
Выполнение этапа 3 «Расчет угла между векторами». Используем способ вычисления скалярного произведения как произведения длин векторов на косинус угла между ними. Поскольку значение скалярного произведения вычислено (этап 2), то единственным неизвестным будет косинус угла между векторами. Найдем его (символьная процедура, вызывается + + ). Длину вектора определяем так, как описано в Пояснении к заданию 3 (идентификатор вектора окружаем вертикальными линиями):
В результате решения получим:
Решение читается так: 
Для того чтобы вывести ответ в градусах, нужно в слот ввести наименование единицы измерения: меню Insert (Вставить) Units (Единицы измерения) Angular (Единицы измерения углов) Degrees (Градусы) Получим (рис. 2.63):
Решение читается так: j = 54.736°.
Этап 3 завершен.
Выполнение этапа 4 «Проверка». Аналогично описанному вычисляем угол между векторами BA и BE. Получаем:
Мы видим, что j + x = p, как и должно быть в параллелограмме. Проверка успешно завершена.
Этап 3 завершен.
Выполнение задания 4 закончено.
§9. Индивидуальные задания по части 2
Индивидуальные задания те же, что в учебной задаче. Индивидуальные исходные данные приведены в табл 3.
Исходные данные к индивидуальным заданиям
🌟 Видео
MathCad вычисление угла между векторами.wmvСкачать

Нахождение угла между векторами через координаты. 9 класс.Скачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Как находить угол между векторамиСкачать

11 класс, 5 урок, Угол между векторамиСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

найти угол между единичными векторамиСкачать

Найти угол между векторами и площадь параллелограмма, построенного на этих векторахСкачать

Математика это не ИсламСкачать

Геометрия 9 класс (Урок№18 - Угол между векторами. Скалярное произведение векторов.)Скачать

100 тренировочных задач #135 Угол между векторамиСкачать

100 Угол между векторамиСкачать

Задание 3 ЕГЭ профиль #121Скачать
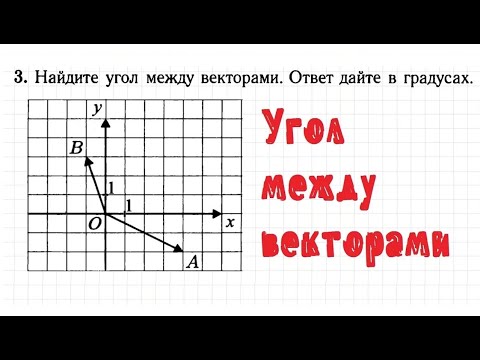
9 класс, 17 урок, Угол между векторамиСкачать

Косинус угла между векторами. Коллинеарность векторовСкачать

105. Угол между векторамиСкачать

Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать



























