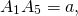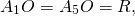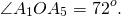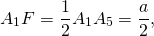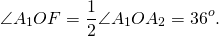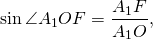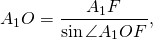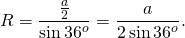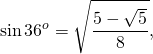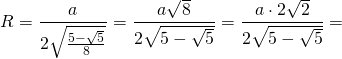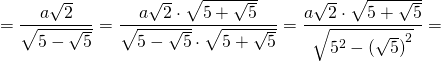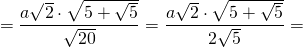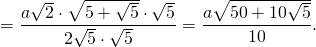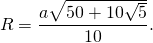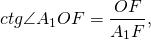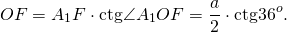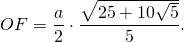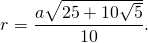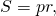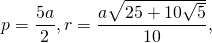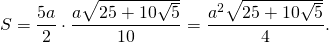Как найти углы вписанного в окружность пятиугольника (7 видео)

Правильный пятиугольник

По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.

Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A₂A₁A₅=108º).

Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна

∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).

Каждый центральный угол правильного пятиугольника, например, угол A₁O A₂, равен

Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.

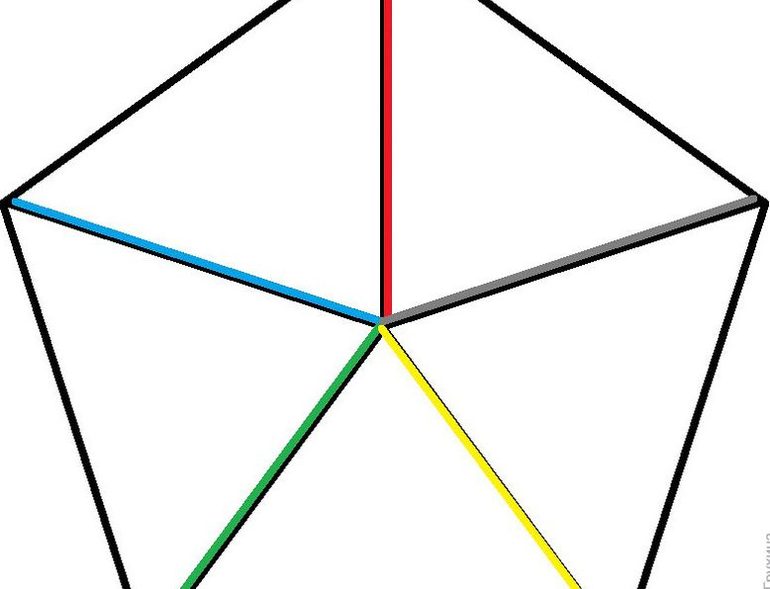
Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.

Основанием каждого такого треугольника равно стороне 5-угольника, боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.

Проведём из вершины высоту OF.

По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A₁OA₅, то есть

Рассмотрим прямоугольный треугольник A₁OF.

Таким образом, формула радиуса описанной около правильного пятиугольника окружности —

Подставив значение котангенса 36°, получаем:

Итак, формула радиуса вписанной в правильный пятиугольник окружности

можно найти площадь правильного пятиугольника. Здесь

Все диагонали правильного пятиугольника равны.

Содержание

Углы пятиугольника вписанного в окружность
Правильный пятиугольник
Правильный пятиугольник — построение, свойства и формулы
Точное построение фигуры
Алгоритм Биона
Приближенные методы
Признаки и свойства
Расчет параметров
Условные обозначения
Соотношения и формулы
Правильный пятиугольник: необходимый минимум информации
Правильный пятиугольник: необходимый минимум информации
🌟 Видео

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Углы пятиугольника вписанного в окружность

Видео:Построение пятиугольника циркулемСкачать

Правильный пятиугольник

По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.

∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).

Каждый центральный угол правильного пятиугольника, например, угол A₁O A₂, равен

Проведём из вершины высоту OF.

Рассмотрим прямоугольный треугольник A₁OF.

Таким образом, формула радиуса описанной около правильного пятиугольника окружности —

Подставив значение котангенса 36°, получаем:

Итак, формула радиуса вписанной в правильный пятиугольник окружности

можно найти площадь правильного пятиугольника. Здесь

Все диагонали правильного пятиугольника равны.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Правильный пятиугольник — построение, свойства и формулы

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Точное построение фигуры

Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:

Построить окружность с центром в некоторой точке О.
Провести два диаметра. Они должны пересекаться под прямым углом.
Поставить точку V (пересечение окружности с одним из диаметров), которая является вершиной фигуры.
По левой стороне поставить точку D. Это пересечение диаметра (оси симметрии) с окружностью.
Отметить на отрезке OD точку А, которая делит его пополам.
Выполнить построение вспомогательной окружности, центром которой является точка, полученная в 5 пункте. Кроме того, круг с радиусом CV должен проходить через V.
Точку, полученную при пересечении диаметра и окружности, нужно обозначить литерой B.
Нарисовать окружность с радиусом, равным CV, из точки V.
Отметить пересечение круга с первой окружностью, центром которой является точка О. Искомое место пересечения обозначить литерой F (вторая вершина пентагона).
Поставить иглу циркуля в точку F и провести окружность через Е.
Обозначить пересечение окружностей с центрами в F и O точкой G, которая будет вершиной пентагона.
Аналогичным образом проделать шаг 11, только центр выбрать не в F, а в G. Полученную точку следует обозначить литерой H (последняя вершина фигуры).
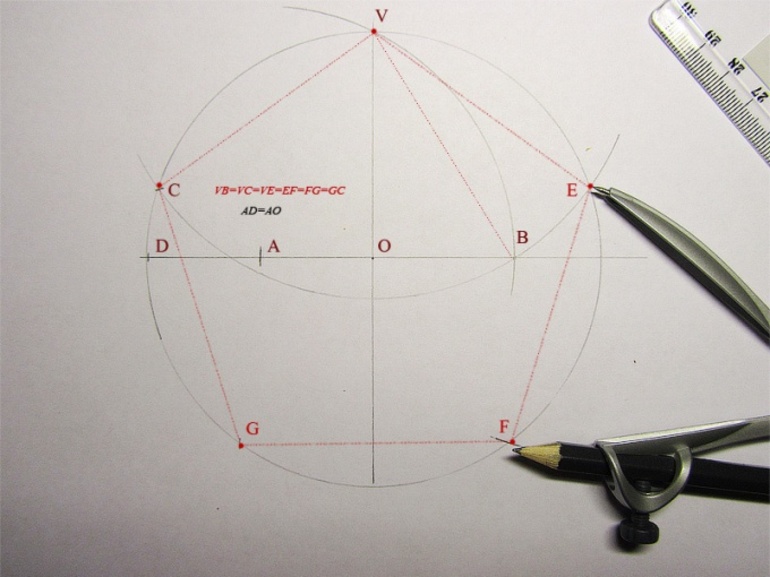
Соединить пять точек (СVEFG) между собой с помощью линейки.

Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:

Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.

Видео:Углы, вписанные в окружность. 9 класс.Скачать

Алгоритм Биона

Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:

Начертить окружность с центром в точке О и радиусом R.
Провести в ней диаметр АD.
Построить правильный (равносторонний) треугольник с одной из сторон, равной диаметру.
Поделить диаметр на несколько равных частей (АС = СE = ED), количество которых вычисляется по формуле: (n — 2). Переменная «n» эквивалентна количеству граней правильного многоугольника, то есть n = 3. Соотношение можно записать следующей зависимостью: АС = [1 / (n — 2)] * AD = AD / 3.
Провести из точек С и Е прямые, перпендикулярные диаметру.
Точки пересечения прямых с окружностью обозначить F и G.
Если соединить точки, то получится пентагон ABDFG.

Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.

Видео:Построение пятиугольника циркулем и линейкойСкачать

Приближенные методы

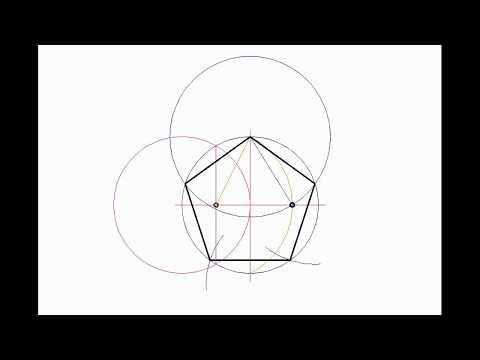
Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).

Метод известного математика А. Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени. Для его реализации следует выполнить определенные шаги алгоритма Дюрера:

Начертить произвольную окружность с центром в точке О.
Не вынимая иглу циркуля из точки О, выполнить построение другой окружности. Ее радиус нужно уменьшить таким образом, чтобы общий радиус R был равен стороне пятиугольника.
Отметить на окружности с большим радиусом две произвольные точки. При этом следует руководствоваться правилом: прямая, проходящая через них, должна касаться малой окружности в одной точке (касательная).
Отметить следующую точку, чтобы можно было соединить ее с предыдущей. Правило при этом должно соблюдаться.
Аналогично проделать операции с другими сторонами пентагона.

Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.

Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.

Видео:Как начертить пятиугольник вписанный в круг или звездаСкачать

Признаки и свойства

Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:

Стороны равны между собой.
Любой угол правильного пятиугольника равен остальным его углам.

Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:

Равенство сторон.
Углы равны по 108 градусов.
Центры вписанной и описанной окружностей совпадают.
Сумма внутренних углов равна 180 * (5 — 2) = 540 (градусов), а внешних — 360.
Количество диагоналей соответствует 5.
Значение площади кольца, которое образуется между вписанным и описанным кругами, эквивалентно произведению квадрата длины стороны на константу Pi / 4.
Биссектрисы, проведенные через центр, равны.
Диагонали — трисектрисы внутренних углов. Одна диагональ делит его на 1/3 и 2/3 части.
Отношение диагонали к стороне эквивалентно «золотому сечению» и равно [1 + 5^(1/2)] / 2.

Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.

Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

Расчет параметров

С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.

Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.

Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.

Условные обозначения

Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:

Сторона: a.
Радиус вписанной и описанной окружностей: r и R соответственно.
Площадь: S.
Периметр и полупериметр: P и p соответственно.
Диагональ: d.
Отношение золотого сечения: Ф.

Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность. Периметром называется сумма всех 5 сторон. Полупериметр вычисляется по следующему соотношению: p = P / 2. Диагонали — отрезки, проведенные из одной вершины к противоположной (несмежной).

Соотношения и формулы

После обозначений следует переходить к рассмотрению основных формул, при помощи которых можно вычислять параметры фигуры. Сторону можно найти, воспользовавшись такими соотношениями:

Радиус вписанной окружности в пентагон можно найти, используя тригонометрические функции. Однако существует также формула, позволяющая вычислить приближенное значение. Это необходимо в том случае, когда под рукой нет специального онлайн-калькулятора, компьютера или таблиц Брадиса. Формулы для нахождения радиуса вписанной окружности:

Математики также рекомендуют описать вокруг пентагона окружность. Это расширит возможности по поиску его основных характеристик. Однако ее радиус следует вычислить. Формулы для его нахождения выглядят таким образом:

Периметр определяется просто: Р = 5а. Значение полупериметра эквивалентно половине периметра, то есть p = P / 2 = 5a / 2 = 2,5a. Площадь можно найти, используя такие формулы:

S = (5a^2 / 4) * ctg(36).
S = 5r^2 * tg(36).
S = 2,5 * R^2 * sin(72).
S = (5/12) * R * d.

Высота правильного пятиугольника (h) — отрезок, проведенный из центра на любую из сторон. Она делит ее на две равные части, поскольку является биссектрисой и медианой равнобедренного треугольника. У последнего две стороны — радиусы описанной окружности, а третья — сторона пентагона. Высота называется также апофемой и проекцией на «а». Вычисляется ее значение по формуле h = a * tg(72) / 2.

Величина Ф является отношением площади пентагона (S) к площади (S1) правильного пятиугольника, полученного при пересечении диагоналей первого: S / S1 = Ф^4 = 3Ф + 2 = (3 * 5^(1/2) + 7) / 2. Длина диагонали находится по такому соотношению: d = [Ф * 5^(1/2) * R]^(1/2).

Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.

Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Правильный пятиугольник: необходимый минимум информации

Толковый словарь Ожегова гласит, что пятиугольник представляет собой геометрическую фигуру, ограниченную пятью пересекающимися прямыми, образующими пять внутренних углов, а также любой предмет подобной формы. Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).

Чем интересен правильный пятиугольник?

Основные свойства и формулы

Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.

Центральный угол α = 360 / n = 360/5 =72°.
Внутренний угол β = 180° * (n-2)/n = 180° * 3/5 = 108°. Соответственно, сумма внутренних углов составляет 540°.
Отношение диагонали к боковой стороне равно (1+√5) /2, то есть «золотому сечению» (примерно 1,618).
Длина стороны, которую имеет правильный пятиугольник, может быть рассчитана по одной из трех формул, в зависимости от того, какой параметр уже известен:

если вокруг него описана окружность и известен ее радиус R, то а = 2*R*sin (α/2) = 2*R*sin(72°/2) ≈1,1756*R;
в случае, когда окружность c радиусом r вписана в правильный пятиугольник, а = 2*r*tg(α/2) = 2*r*tg(α/2) ≈ 1,453*r;
бывает так, что вместо радиусов известна величина диагонали D, тогда сторону определяют следующим образом: а ≈ D/1,618.

Площадь правильного пятиугольника определяется, опять-таки, в зависимости от того, какой параметр нам известен:
если имеется вписанная или описанная окружность, то используется одна из двух формул:

S = (n*a*r)/2 = 2,5*a*r либо S = (n*R 2 *sin α)/2 ≈ 2,3776*R 2 ;

площадь можно также определить, зная лишь длину боковой стороны а:

S = (5*a 2 *tg54°)/4 ≈ 1,7205* a 2 .

Правильный пятиугольник: построение

1. Выберите произвольный радиус и начертите окружность, обозначив ее центр точкой O.

2. На линии окружности выберите точку, которая будет служить одной из вершин нашего пятиугольника. Пусть это будет точка А. Соедините точки О и А прямым отрезком.

3. Проведите прямую через точку О перпендикулярно к прямой ОА. Место пересечения этой прямой с линией окружности обозначьте, как точку В.

4. На середине расстояния между точками О и В постройте точку С.

5. Теперь начертите окружность, центр которой будет в точке С и которая будет проходить через точку А. Место ее пересечения с прямой OB (оно окажется внутри самой первой окружности) будет точкой D.

6. Постройте окружность, проходящую через D, центр которой будет в А. Места ее пересечения с первоначальной окружностью нужно обозначить точками Е и F.

7. Теперь постройте окружность, центр которой будет в Е. Сделать это надо так, чтобы она проходила через А. Ее другое место пересечения оригинальной окружности нужно обозначить точкой G.

8. Наконец, постройте окружность через А с центром в точке F. Обозначьте другое место пересечения оригинальной окружности точкой H.

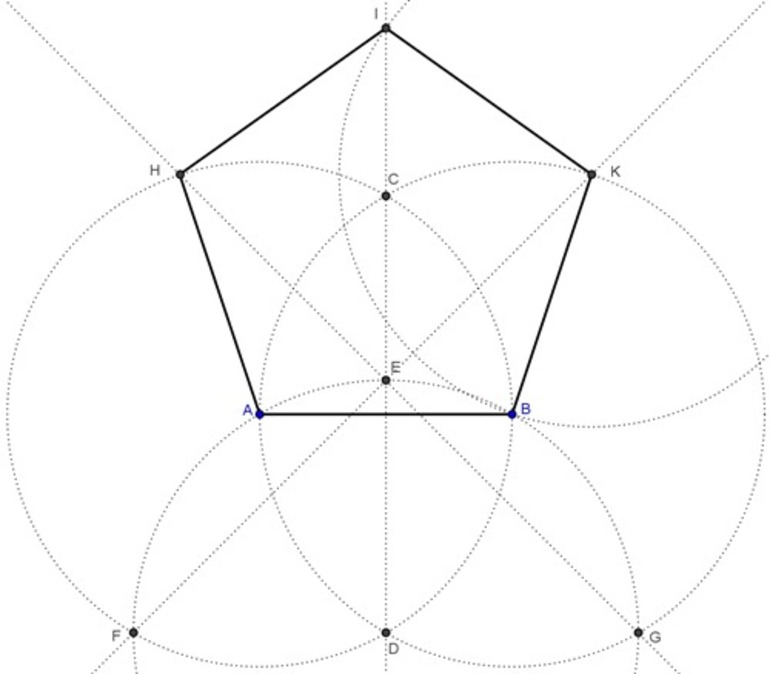
9. Теперь осталось только соединить вершины A, E, G, H, F. Наш правильный пятиугольник будет готов!

Видео:Геометрия - Построение шестиугольникаСкачать

Правильный пятиугольник: необходимый минимум информации

Чем интересен правильный пятиугольник?

Основные свойства и формулы

Центральный угол α = 360 / n = 360/5 =72°.
Внутренний угол β = 180° * (n-2)/n = 180° * 3/5 = 108°. Соответственно, сумма внутренних углов составляет 540°.
Отношение диагонали к боковой стороне равно (1+√5) /2, то есть «золотому сечению» (примерно 1,618).
Длина стороны, которую имеет правильный пятиугольник, может быть рассчитана по одной из трех формул, в зависимости от того, какой параметр уже известен:

если вокруг него описана окружность и известен ее радиус R, то а = 2*R*sin (α/2) = 2*R*sin(72°/2) ≈1,1756*R;
в случае, когда окружность c радиусом r вписана в правильный пятиугольник, а = 2*r*tg(α/2) = 2*r*tg(α/2) ≈ 1,453*r;
бывает так, что вместо радиусов известна величина диагонали D, тогда сторону определяют следующим образом: а ≈ D/1,618.

Площадь правильного пятиугольника определяется, опять-таки, в зависимости от того, какой параметр нам известен:
если имеется вписанная или описанная окружность, то используется одна из двух формул:

S = (n*a*r)/2 = 2,5*a*r либо S = (n*R 2 *sin α)/2 ≈ 2,3776*R 2 ;