Как найти центр тяжести четверти окружности

Видео:Найти центр кругаСкачать

Статические моменты площади сечения. Центр тяжести площади сечения

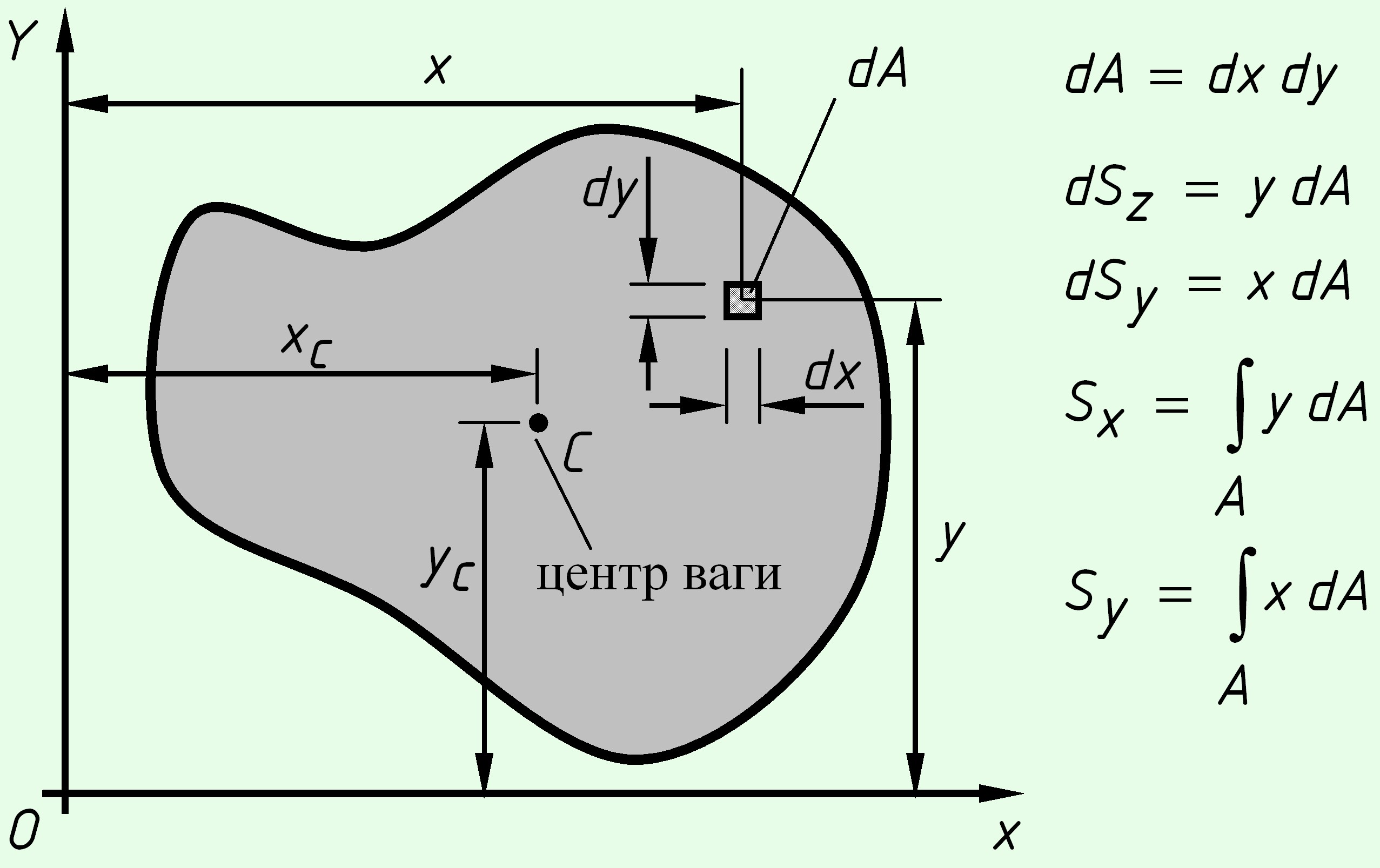
Рассмотрим произвольное поперечное сечение стержня, связанный с координатными осями $XOY$ и выделим элемент площади $dA$ с координатами ($x,y$).

Статическим моментом площади сечения относительно оси называется сумма (интеграл) по всей площади сечения от произведения площади элементарной площадки на расстояние до рассматриваемой оси.

Для сечений, для которых известны площади $A$ и координаты центров тяжести $$, $$, статические моменты площадей рассчитываются по формулам:

Статический момент площади сечения может быть положительным, отрицательным и равняться нулю.

Оси, относительно которых статические моменты площади сечения равны нулю, называются центральными.

Видео:Найдите центр тяжестиСкачать

Примеры определения статических моментов

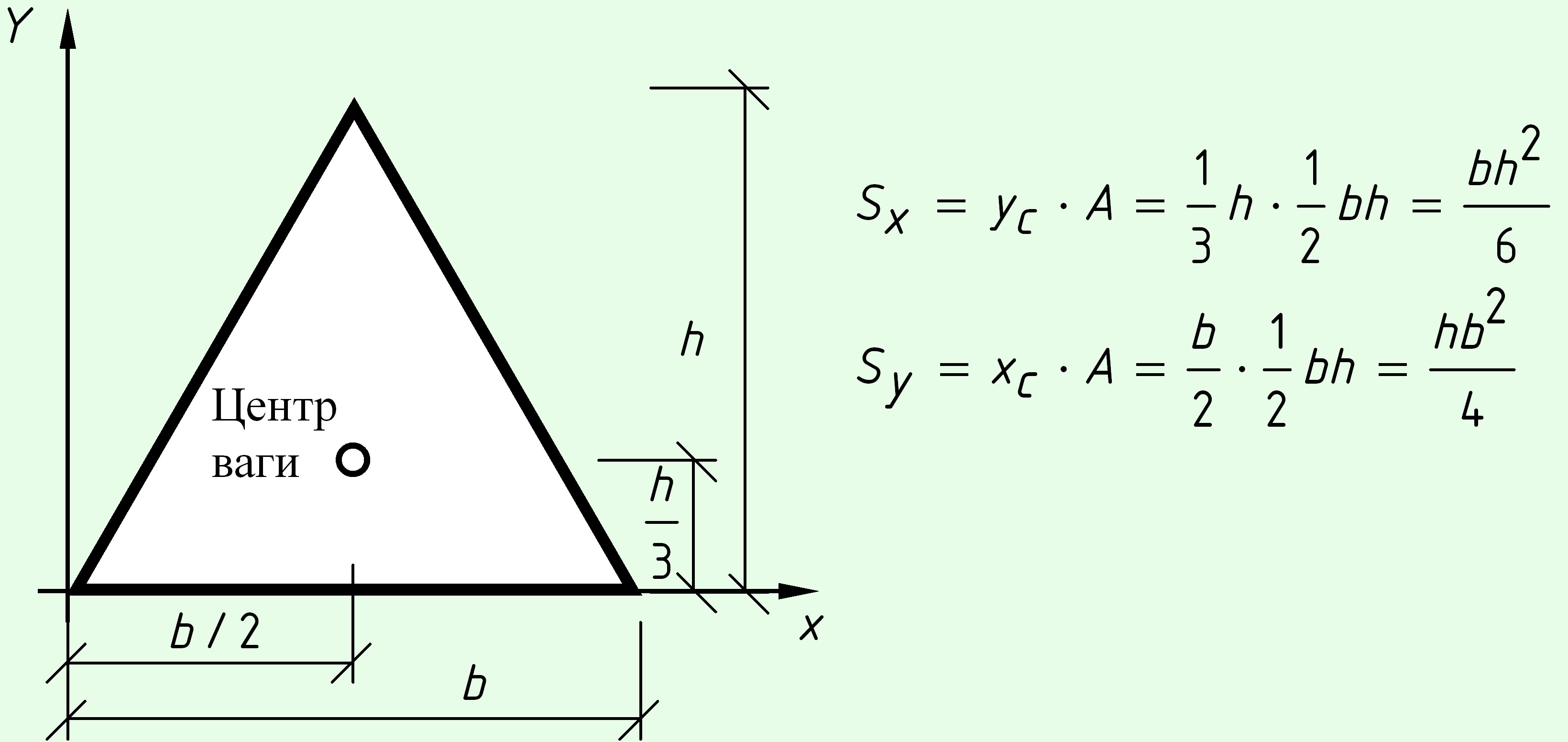
Треугольник.

Поскольку положение центра тяжести треугольника нам известно, его статический момент площади можно определить как произведение площади на соответствующую координату центра тяжести.

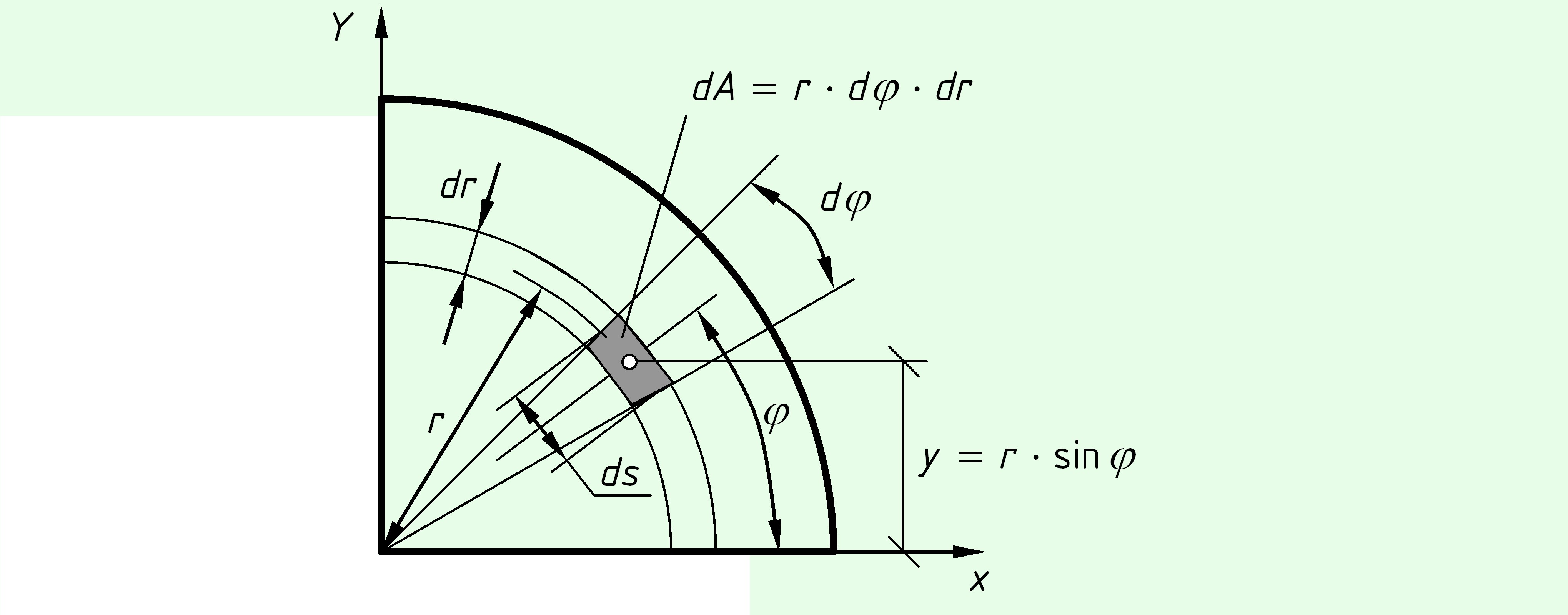
Четверть круга.

Поскольку положение центра тяжести четверти круга мы не знаем, определим статические моменты по общей формуле. Выделим элементарную площадь $dA$ с углом $dvarphi $ и высотой $dr$. Ширина площадки $ds = r cdot dvarphi ,$.

Площадь $A = frac cdot pi $.

Аналогично относительно другой оси $ = frac<<>> = frac<><>$.

Статический момент составного сечения равен сумме статических моментов его составляющих.

Тогда положение центра тяжести составного сечения запишется так:

Видео:Центр кругаСкачать

Статические моменты и координаты центра тяжести

Видео:Видеоурок 3. Определение центра тяжести.Скачать

Вычисление статических моментов и координат центра тяжести кривой

а) Пусть материальная точка массы отстоит от оси на расстоянии . Статическим моментом этой точки относительно оси называют число . Статическим моментом системы материальных точек , расположенных по одну сторону от оси , массы которых равны , а расстояния от оси равны называют число

Если же эти точки расположены по разные стороны от оси, то для точек, находящихся по одну сторону оси, расстояния берутся положительными, а для точек по другую сторону от оси — отрицательными.

Поэтому если точки расположены на координатной плоскости,

где — статический момент относительно оси и — относительно оси .

б) Рассмотрим теперь случай, когда масса равномерно распределена по некоторой кривой или по некоторой области . Будем считать, что плотность распределения равна единице. Тогда масса дуги численно равна ее длине, а масса области — ее площади.

Начнем со случая кривой линии , задаваемой уравнением , причем предположим, что функция непрерывна и неотрицательна.

Как обычно, разобьем отрезок на части точками и обозначим через и наименьшее и наибольшее значения функции на отрезке , Этому разбиению соответствует разбиение дуги на части (рис. 60). Из физических соображений ясно, что статический момент части относительно оси абсцисс заключен между и , где —длина этой части, (напомним, что мы положили линейную плотность дуги равной единице). Таким образом,

Так как на отрезке выполняется неравенство

то в тех же границах, что и , заключен интеграл . Значит,

Этот интеграл обозначают также следующим образом: или .

Физики обычно заменяют проведенное рассуждение более коротким. Они берут «бесконечно малый участок дуги» . Его статический момент равен . А статический момент всей дуги равен сумме элементарных статических моментов, т. е. . Преимуществом этого вывода является его наглядность. Однако в нем не определено, что такое «бесконечно малый участок дуги», или как еще говорят, «элемент дуги». При уточнении этого понятия мы вновь приходим к более длинному выводу, изложенному ранее. В дальнейшем для краткости изложения мы будем использовать принятый в физике метод рассуждений. С его помощью сразу выводим, что

Как формула (1), так и формула (2) верны и в случае, когда кривая пересекает оси координат.

в) Введем понятие центра тяжести.

Определение. Центром тяжести тела называется такая точка , что если в ней сосредоточить всю его массу, то статический момент этой точки относительно любой оси будет равен статическому моменту всего тела относительно той же оси.

Обозначим через и расстояния центра тяжести кривой от осей ординат и абсцисс.

Тогда, пользуясь определением центра тяжести кривой, получим:

Разрешая полученные равенства относительно и , найдем координаты центра тяжести плоской кривой

Замечание. Если кривая расположена симметрично относительно некоторой прямой, то центр тяжести такой кривой находится на этой прямой.

Это замечание позволяет в некоторых случаях упростить нахождение координат центра тяжести плоской кривой.

Пример 1. Найти статический момент полуокружности относительно диаметра.

Решение. Выберем систему координат так, чтобы центр окружности совпал с началом координат, а диаметр, относительно которого мы ищем статический момент, совпал с осью . Тогда статический момент полуокружности относительно диаметра выразится формулой

В выбранной системе координат уравнение полуокружности запишется так: . Тогда

Пример 2. Найдем центр тяжести четверти окружности , расположенной в первом квадранте.

Решение. Данная кривая расположена симметрично относительна биссектрисы первого координатного угла, следовательно, центр тяжести этой кривой лежит на биссектрисе, а потому . Достаточно найти только .

Вычисление проще провести, перейдя к параметрическим уравнениям окружности. Так как ее радиус равен двум, то для четверти окружности имеем:

Отсюда находим, что и

Поскольку длина четверти данной окружности равна , то

Видео:Определение центра тяжести сложной фигуры. СопроматСкачать

Вычисление статических моментов и координат центров тяжести плоских фигур

Найдем статический момент прямоугольника со сторонами и относительно стороны . Разобьем этот прямоугольник на элементарные прямоугольники, имеющие стороны и (рис. 61). Масса элементарного прямоугольника равна его площади (напомним, что по предположению плотность распределения массы равна единице). Поэтому элементарный статический момент равен , а статический момент всего прямоугольника равен

Теперь уже легко найти статический момент криволинейной трапеции, ограниченной сверху кривой , где — непрерывная и неотрицательная функция на отрезке , снизу осью абсцисс, а с боков прямыми .

Разобьем криволинейную трапецию на элементарные прямоугольники, основание каждого из которых равно и высота . Статический момент такого прямоугольника относительно оси абсцисс по формуле (1) равен , а потому статический момент всей криволинейной трапеции равен . В случае, когда не выполняется предположение о неотрицательности функции , эту формулу надо заменить такой:

(части фигуры, расположенные ниже оси абсцисс, дают отрицательный вклад в ).

Поскольку по предположению плотность равна единице, то масса криволинейной трапеции равна ее площади, т. е. интегралу , а потому ордината центра тяжести этой трапеции выражается формулой

Нетрудно найти и статический момент криволинейной трапеции относительно оси ординат. Для этого достаточно заметить, что расстояние элементарного прямоугольника от этой оси равно . Поэтому его статический момент равен , а статический момент всей трапеции выражается формулой

Пример 3. Найти статический момент (относительно оси ) фигуры, ограниченной осью абсцисс и одной аркой циклоиды:

Решение. Так как параметр одной арки циклоиды изменяется от до , то

Пример 4. Найти центр тяжести фигуры, ограниченной осью и одной полуволной синусоиды .

Решение. Так как фигура под полуволной синусоиды расположена симметрично относительно прямой , то центр тяжести лежит на этой прямой и, следовательно, . Ордината центра тяжести находится по формуле .

Итак, центр тяжести данной фигуры находится в точке .

Пример 5. Найти центр тяжести фигуры, ограниченной осью абсцисс и одной аркой циклоиды .

Решение. Данная фигура расположена симметрично относительно прямой , следовательно, центр тяжести ее находится на этой прямой, и потому . Найдем по формуле .

Площадь данной фигуры была вычислена раньше, она равна . Следовательно,

Центр тяжести данной фигуры находится в точке .

Видео:Определение центра тяжести сложных сечений. Фигуры из ГОСТ.Скачать

Центры тяжести некоторых однородных тел

Центр тяжести площади треугольника. Разобьем площадь треугольника ABD на ряд узких полосок, параллельных стороне AD (рис. 5.3). Центр тяжести каждой такой элементарной полоски находится в ее середине, а центры тяжести всех этих полосок будут лежать на медиане BE. Разбив площадь треугольника прямой, параллельной его другой стороне, например стороне АВ, убедимся, что центр тяжести треугольника должен лежать на медиане DK. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке С пересечения его медиан. Точка пересечения медиан делит каждую медиану в отношении 2 : 1, т. е. СЕ= (1/3)ВЕ, СВ = (2/3)BE.

Если известны координаты вершин данного треугольника А(х_Л, у A, Z_A), В(х_в, у_в, Z_B), D(x_d, y_D, Z_D), TO по формулам аналитической геометрии получим координаты центра тяжести С:

Центр тяжести дуги окружности. Рас-

смотрим дугу АВ радиусом R с центральным углом АОВ= 2а. Ввиду симметрии центр тяжести этой дуги лежит на оси

Ох (рис. 5.4). Выделим на дуге АВ элемент ab длиной dl = Rdiр, положение которого определяется углом ф. Координата х элемента ab будет х = R cos ф. Подставляя значения хи dl в первую из формул (5.8), заменив в ней знак суммирования на интеграл по всей

длине дуги АВ, получим

где L — длина дуги АВ, равная R • 2а. Отсюда окончательно находим, что центр тяжести дуги окружности лежит на оси ее симметрии на расстоянии от центра О, равном

где угол а измеряется в радианах.

Центр тяжести кругового сектора. Рассмотрим круговой сектор ОАВ радиусом R с центральным углом 2а (рис. 5.5). Разобьем площадь сектора ОАВ радиусами, проведенными из центра О, на элементарные секторы, каждый из которых можно рассматривать как

треугольники, центры тяжести которых лежат на дуге DE окружности радиусом 2R/2. Следовательно, центр тяжести сектора ОАВ совпадает с центром тяжести дуги DE, положение которого определится по формуле (5.10), подставив в нее значение радиуса 2/?/3:

В частности, для полукруга будем иметь a = я/2 и из (5.11) получим:

Приведем без доказательства еще некоторые результаты.

Центр тяжести призмы. Чтобы найти центр тяжести призмы, мысленно разобьем ее плоскостями, параллельными основанию, на тонкие пластины, которые можно принять за плоские многоугольники. Учитывая, что все они будут одинаковыми, то их центры тяжести лежат на отрезке прямой, соединяющей центры тяжести С| нижнего и С₂ верхнего оснований этой призмы, а центр тяжести С всей призмы находится в середине указанного отрезка (рис. 5.6).

Центр тяжести пирамиды (конуса). Этот центр С лежит на отрезке прямой, соединяющей вершину пирамиды с центром тяжести ее основания, на расстоянии 1/4 этого отрезка от центра тяжести основания. Так, для пирамиды и конуса, изображенных на рис. 5.7,

Этот результат справедлив для любой многоугольной пирамиды и для конуса.

Центр тяжести полушара. Этот центр С лежит на оси Ох (ось симметрии, рис. 5.8), а его координата

где R — радиус полушара.

Задача 5.1. Из тонкой однородной проволоки сделан контур (рис. 5.9, а), представляющий собой две дуги полуокружностей радиусов R и г = R/2 и прямую AD. Определить центр тяжести контура.

Решение. Проводим оси Dxy и разбиваем контур на три элемента, для каждого из которых находим его длину и координаты центра тяжести.

Дуга АВ радиусом /?(/, = nR, х_< = 0, у _<— 2R/n, последнее получим из

формулы (5.10), положив а — п/2), дуга DB радиусом r—R/2(l₂ — nR/2,

Подставив соответствующие значения в формулы (5.8), получим

Найденное положение центра тяжести С контура показано на рис. 5.9, а.

Задача 5.2. Определить центр тяжести пластины, ограниченной контуром, рассмотренным в предыдущей задаче.

Проводим оси Dxy (рис. 5.9, б) и разбиваем пластину на два элемента: полукруг радиусом R (ч. 1), из которого вырезан полукруг радиусом г = R/2 (ч. 2).

При выполнении расчетов площадь части 2, как вычитаемая, должна браться со знаком «минус». Тогда для каждой части имеем:

Подставив числовые значения величин в формулы (5.7), получим

Центр тяжести С, координаты которого определены, показываем на чертеже (рис. 5.9, б); он располагается на прямой С_ХС₂ левее точки С_х.

Сопоставив результаты задач 5.1 и 5.2, видим, что центр тяжести пластины (рис. 5.9, б) не совпадает с центром тяжести контура (рис. 5.9, а), окаймляющего ее.

Задача 5.3. Определить положение центра тяжести однородной пластины, изображенной на рис. 5.10 (размеры даны в сантиметрах).

Решение. Проводим оси Вху. Площадь пластины рассматриваем как фигуру, составленную из трех частей: треугольника ЛВК (ч. 1) и прямоугольника BKED (ч. 2), из которого вырезан полукруг (ч. 3) радиусом R = 3 см.

Вычисляем площадь и координаты центров тяжести каждой части пластины:

S₃ = —uF?/2 — —14,13 см 2 (площадь полукруга берем со знаком минус, так как она вычитается из площади прямоугольника), х₃ = 8 — 4/?/Зтг = 6,73 см, у₃ = 3 см.

Площадь всей пластины S = о) + S₂ + о₃ = 42,87 см .

Подставив соответствующие значения в формулы (5.7), получим:

Найденное положение центра тяжести С показываем на чертеже.

Задача 5.4. Определить положение центра тяжести однородного твердого тела (рис. 5.11), состоящего из трех частей: полушара I радиусом /?, прямого круглого цилиндра II радиусом г — /?/2 и высотой Н — 4/?, круглого конуса III с основанием радиусом /? и высотой h = 2/?.

Решение. Проводим оси координат Oxyz так, что ось у совмещена с осью симметрии тела. Тогда х_с— 0, Zq

Обозначим центры тяжести полушара через С_х, цилиндра — через С₂, конуса — через С₃. Для вычисления у_с воспользуемся формулой (5.6), которая в данном случае имеет вид:

где у_х, у₂, у₃ — координаты центров тяжести полушара, цилиндра и конуса; V], v₂, v₃ — соответственно объемы этих тел; общий объем V— v, + v₂ + v₃.

Находим: для полушара I v_x — 2kR 3 /3, y_x= — 3R/8 для цилиндра II v₂ = nr 2 H= kR 3 , у₂ = Н/2 = 2R; для конуса III v₃ = nF^h/3 = 2nR 3 /3, у₃ =

= // + -h -4,5R, V-7nR /3. Подставив эти значения в формулу, получим У _с — (57/28) /?.

Ответ: положение центра тяжести С данного твердого тела (см. рис. 5.11) определяется координатами х_с— 0, у_с — (57/28)/?, ?_с= 0.

🔍 Видео

Как найти центр у любой окружности 🤔Скачать

Как найти центр круга с помощью подручных средств? ЛЕГКО.Скачать

Геометрия Задача найти центр круга /math and magicСкачать

Как найти центр тяжести любой фигуры?Скачать

Найти центр и радиус окружностиСкачать

4K Как найти центр окружности, how to find the center of a circleСкачать

Быстро и легко определяем центр любой окружностиСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Не каждый знает как найти центр окружности без циркуля! #ShortsСкачать

Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать

Возьми на заметку! Как быстро найти центр окружности.#shortsСкачать

Центр тяжести. ЭкспериментСкачать

6.1. Центр тяжести линииСкачать

Определение центра тяжести плоской фигуры. Подробное объяснение. Сопромат для чайниковСкачать