Как найти сопротивление окружности

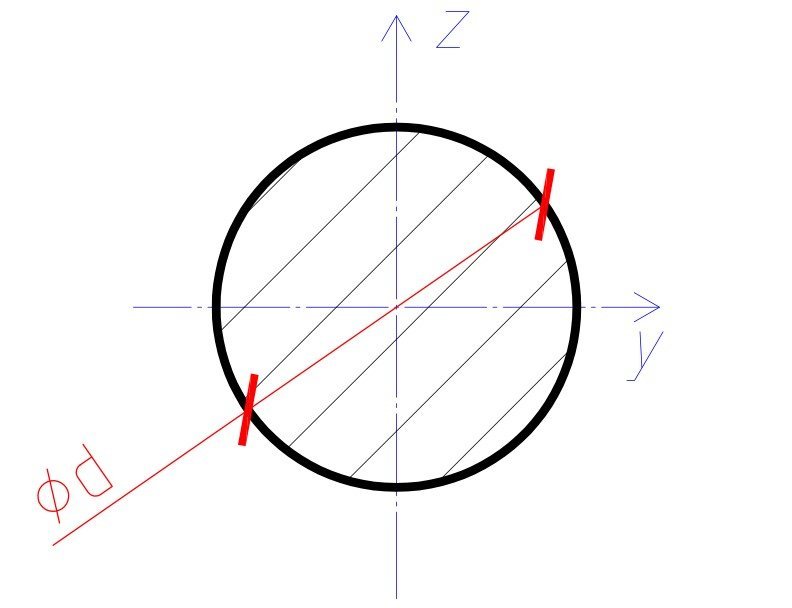
d — диаметр сечения круга в мм; y, z — центральные оси сечения.

Введите диаметр сечения d в мм:

В результате момент сопротивления относительно центральных осей y и z равны W_y = W _z =

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Как найти момент сопротивления круга?

Момент сопротивления круга относительно центральной оси z равен моменту сопротивления относительно центральной оси y и рассчитывается по формуле:

W_y = W_z = Π . d 3 /32,

W_y — момент сопротивления относительно центральной оси y в мм 3 ;

W_z — момент сопротивления относительно центральной оси z в мм 3 ;

d — диаметр круга в мм.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Математическая конструкция и свойства диаграммы Вольперта-Смита

Диаграмма Вольперта-Смита – инструмент, чрезвычайно полезный для инженеров и разработчиков, занимающихся радиочастотными цепями. В данной статье рассматривается математика создания диаграммы и её объяснение с точки зрения физики.

Видео:1 2 4 сопряжение окружностейСкачать

Введение

Диаграмма Вольперта-Смита используется с 1930-х годов в качестве метода решения различных задач проектирования в диапазоне радиочастот – в частности, согласование комплексных сопротивлений с помощью последовательно и параллельно включенных элементов – и обеспечивает удобный способ для нахождения решения без использования калькулятора. Для того, чтобы понять конструкцию диаграммы, вы должны понимать алгебру на уровне средней школы и основы комплексных чисел, а также иметь общее представление о комплексном сопротивлении (импедансе) в электронных схемах. Тем не менее, даже если вы не в совсем поймете приведенный ниже вывод, вы всё равно можете использовать диаграмму в своих разработках. Взяв стандартную формулу коэффициента отражения и манипулируя ею так, чтобы получить уравнения окружностей различных радиусов, мы сможем построить базовую диаграмму Вольперта-Смита. Это всё, чем на самом деле и является диаграмма Вольперта-Смита: набор окружностей, центры которых находятся в разных местах на графике или за его пределами, и каждая из которых представляет собой либо постоянное активное сопротивление, либо постоянное реактивное сопротивление.

Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать

Получение диаграммы Вольперта-Смита

После того, как мы закончим вывод диаграммы, ниже будет приведено несколько упрощенных изображений, показывающих, как полученные формулы могут быть использованы для получения конечного результата. Давайте начнем с формулы коэффициента отражения в зависимости от сопротивлений источника и нагрузки:

Коэффициент отражения – это просто отношение амплитуды отраженной волны к амплитуде падающей волны. Это главная формула, которую мы будем использовать, но с небольшими преобразованиями. Во-первых, нам необходимо немного упростить ее путем нормализации относительно Z_нагр, разделив каждый член в правой части формулы на Z_нагр:

Напомним, что Z_O является комплексным значением импеданса и может быть представлено в виде R + jX . Так как коэффициент отражения (который сейчас находится в полярной форме) может быть также представлен и в прямоугольных координатах (для этого мы будем использовать A + jB ), приведенная выше формула может быть преобразована в следующую:

Круто! На данный момент мы получили уравнение в том виде, который нам необходим, чтобы начать построение диаграммы Вольперта-Смита. Следующий шаг – решение для действительной и мнимой частей равенства – возможно, самая сложная часть всего вывода, и даже тогда вам надо просто понимать идею комплексных сопряжений, чтобы выполнить этот шаг. Давайте продолжим и разделим уравнение на действительную и мнимую составляющие, сначала умножив на комплексное сопряженное число (это поможет, если вы разделите существующие действительные и мнимые части, используя скобки, как показано ниже):

Теперь мы можем отделить действительную и мнимую составляющие. После чего необходимо будет выполнить два последних упрощения, и мы получим формулы для построения диаграммы Вольперта-Смита. Ниже приведены разделенные действительная и мнимая составляющие (назовем их уравнения 1 и 2):

И, наконец, вам необходимо выполнить несколько алгебраических операций, чтобы вывести зависимость X 2 от A. В итоге получится уравнение 3:

Это можно подставить в уравнение 2, чтобы получить первое из двух конечных уравнений, которое позволит нам определить круги постоянного активного сопротивления (уравнение 4):

Выглядит знакомо? Это окружность радиусом (frac) и центром в точке ((frac,; 0)) . Изменяя значение R в уравнении, можно нарисовать каждую из окружностей на диаграмме Вольперта-Смита.

Аналогичным образом, выразив R (я использовал уравнение 2), вы получите решения выглядящие следующим образом:

И, подставив это выражение в уравнение 1 и упростив полученное выражение, получим следующий результат:

Как и предыдущий результат, это окружность радиусом (frac) , но на этот раз у нас два набора окружностей с центрами в ((1, 1/X)) . Это окружности (они появятся в виде дуг на диаграмме) постоянного реактивного сопротивления. Теперь вы можете увидеть, как строится диаграмма Вольперта-Смита, она состоит из окружностей постоянного активного сопротивления и дуг постоянного реактивного сопротивления. Ниже вы можете увидеть упрощенные изображения обоих уравнений, построенные по отдельности и вместе. Но сначала давайте поговорим о том, как интерпретировать диаграмму Вольперта-Смита с точки зрения физики.

Из полученных нами уравнений можно получить довольно много информации. Вот несколько моментов, на которые стоит обратить внимание:

1. при бесконечных R и X оба типа окружностей сходятся в одном месте (обычно изображается на крайне правой или на крайне левой стороне диаграммы). Это точка с координатами (1, 0) ;
2. установка R = 0 приведет к окружности с центром в точке (0, 0) на вашей диаграмме и с радиусом 1, который является «границей» диаграммы;
3. установка X = 0 приведет к бесконечному радиусу; это соответствует линии, пересекающей центр диаграммы. Как мы можем это интерпретировать? Эту линию часто называют действительной осью. Касательно реактивного сопротивления, линии выше действительной оси на диаграмме (положительные дуги из второго полученного уравнения) представляют собой индуктивные реактивные сопротивления, а линии ниже (отрицательные дуги) – емкостные реактивные сопротивления;
4. что произойдет, если R ? Стандартная диаграмма Вольперта-Смита не дает информации об этом, но ситуации с R , лежащим за границами диаграммы, предполагают возникновение колебаний в любой возможной цепи (что очень полезно знать);
5. на основе знаний, которые у нас теперь есть, об активном и реактивном сопротивлениях на диаграмме, мы знаем, что каждая точка представляет собой последовательную комбинацию активного и реактивного сопротивлений ( R + jX ). Это поможет нам при разработке.

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

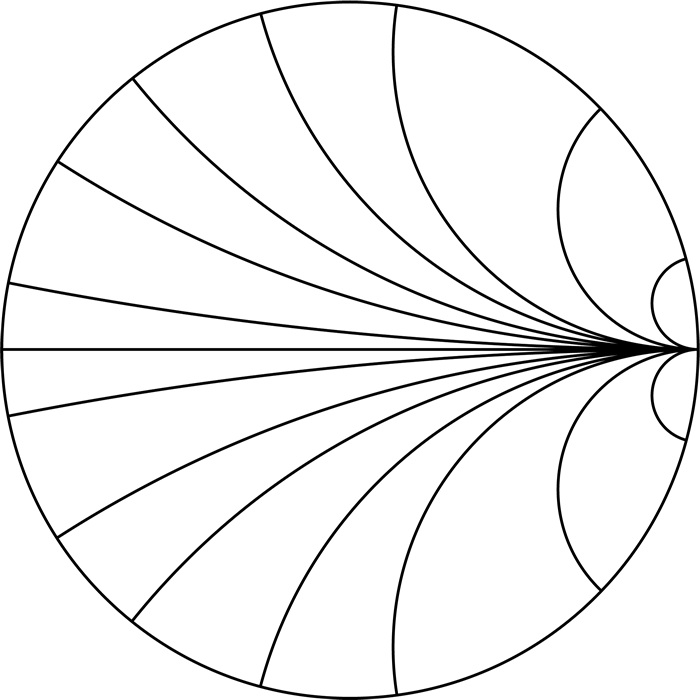
Окружности постоянного активного сопротивления

Видео:КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Дуги постоянного реактивного сопротивления

Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

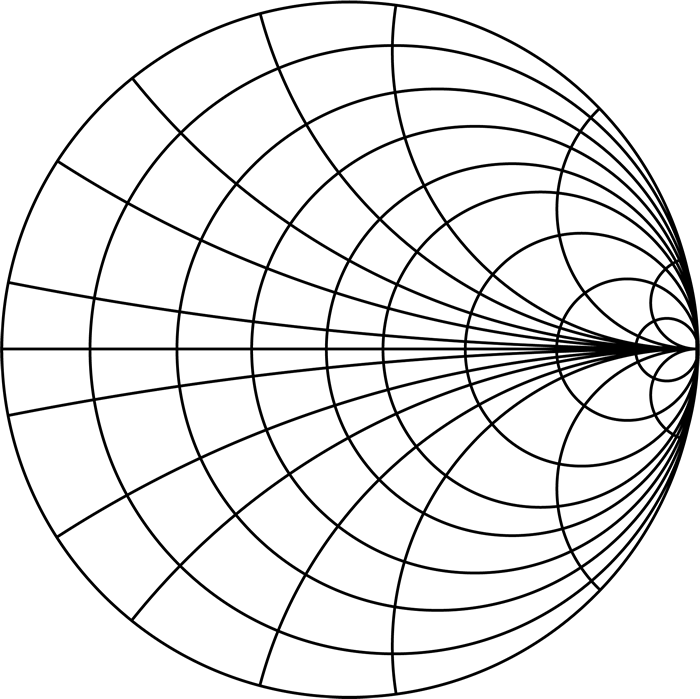
Окружности постоянного активного сопротивления и дуги постоянного реактивного сопротивления: базовая диаграмма Вольперта-Смита

Видео:Найти центр кругаСкачать

Использование диаграммы Вольперта-Смита для работы с комплексными сопротивлениями

Так как же использовать диаграмму Вольперта-Смита? Для нанесения на диаграмму импеданса при расчете согласования комплексных сопротивлений лучше всего определить соответствующую окружность постоянного активного сопротивления (ту, которая соответствует действительной части вашего импеданса), а затем перемещаться по ее дуге, пока не найдете пересечение с соответствующим значением реактивного сопротивления.

Например, предположим, у вас есть комплексное сопротивление Z = 0,3 – 0,6j . Сначала найдите окружность постоянного активного сопротивления 0,3 . Так как ваше сопротивление имеет отрицательное комплексное значение, то это представляет собой емкостное комплексное сопротивление в теоретической цепи, и вы должны двигаться против часовой стрелки по окружности активного сопротивления 0,3 , чтобы найти, где она пересекается с дугой реактивного сопротивления –0,6 (если бы это значение было положительным, то оно представляло бы собой индуктивное реактивное сопротивление, и вы бы двигались по часовой стрелке). Вы можете продолжать выполнение построения для расчета согласования импедансов для ваших цепей, так как диаграмма Вольперта-Смита интуитивно понятна и в этом случае чрезвычайно полезна. Вам необходимо только выполнить следующие действия:

1. зная значение комплексного сопротивления нагрузки, найти его на диаграмме Вольперта-Смита и использовать его в качестве начальной точки;
2. если вы знаете выходное сопротивление источника, вы можете добавить последовательно компоненты (шунты будут упомянуты ниже) путем добавления и вычитания значений реактивных сопротивлений до тех пор, пока не получите необходимый импеданс.

Важно обратить внимание на два момента:

1. на практике вы часто можете обнаружить, что цифры на вашей диаграмме малы по сравнению со значениями составляющих комплексного сопротивления, которые вы хотите найти. Здесь снова вступает в игру нормализация; часто бывает удобнее всего нормализовать импеданс (например, Z = 200 + j400 ), в результате вы работаете с ним, деленным на некоторое значение, что делает построение диаграммы проще (часто это значение действительной части импеданса, но вы можете использовать и любое другое удобное для вас значение). Таким образом, вы сможете работать на менее заполненном участке диаграммы Вольперта-Смита, что приводит нас к следующему пункту;
2. при работе с диаграммой Вольперта-Смита легко оказаться в ситуации, когда вы будете вынуждены работать со значениями комплексных сопротивлений близко к точке ( 1, 0 ), и в этом случае у вас возникнут проблемы с ошибками в рассчитанных вами значениях. Вот поэтому лучше всего нормализовать значения вашего импеданса при работе с диаграммой, что позволит вам работать с более широкими дугами при согласовании импедансов и обеспечит постоянную точность по мере добавления компонентов в последовательность.

Видео:Физика - Электричество. Найти общее сопротивление цепи 1Скачать

Последнее замечание – комплексная проводимость и диаграммы иммитанса (комплексных сопротивления и проводимости)

До сих пор мы не упоминали о комплексной проводимости на диаграмме Смита. Если вы не знаете, то комплексная проводимость (адмиттанс) является величиной, обратной комплексному сопротивлению (импедансу), или (Y=frac) . Активное и реактивное сопротивления в этом случае соответствуют активной и реактивной проводимостям. На самом деле, построить аналогичную диаграмму для проводимостей удивительно просто – всё, что вам нужно сделать, это отразить диаграмму сопротивлений по горизонтали. Подобное преобразование очень важно, так как теперь у вас есть диаграмма, которая поможет вам при работе с шунтирующими компонентами (включенными между корпусом и линией связи, параллельно источнику и нагрузке), а не только с включенными последовательно.

Процесс нанесения проводимости на диаграмму противоположен – при добавлении индуктивности в цепь последовательно необходимо перемещать значение импеданса по часовой стрелке вдоль окружности постоянного активного сопротивления, а при добавлении шунтирующей индуктивности (включенной параллельно) необходимо перемещаться против часовой стрелки вдоль окружности постоянной активной проводимости; аналогично и с конденсаторами, шунтирующий конденсатор перемещает ваши значения по часовой стрелке на диаграмме комплексной проводимости, а конденсатор, включенный последовательно, – против часовой.

Сочетание обоих типов диаграмм даст вам то, что называется диаграммой комплексных сопротивления и проводимости (иммитанса), которая (как только вы добавите еще несколько деталей, не описанных в данной статье) становится еще более полезной, чем стандартная диаграмма Смита, хотя она и будет выглядеть более устрашающей для тех, кто не знает, как она была создана.

Надеюсь, эта статья дала вам ясное понимание того, как строится и как работает диаграмма Смита. В случае вопросов оставляйте комментарии ниже.

Видео:Как искать точки на тригонометрической окружности.Скачать

Закон Ома

О чем эта статья:

8 класс, 10 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Как найти центр круга с помощью подручных средств? ЛЕГКО.Скачать

Сопротивление

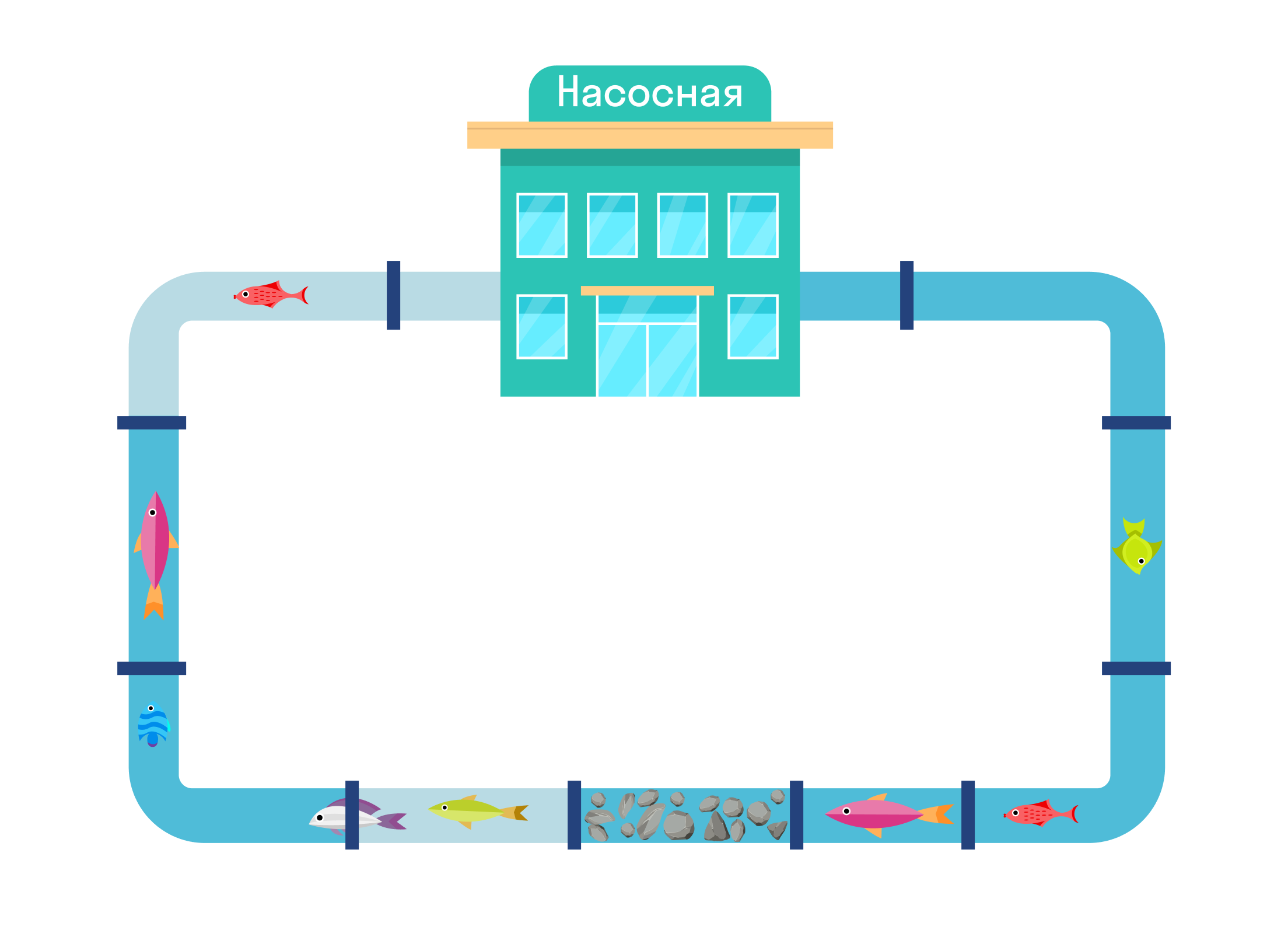
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.

• Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.

Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.

Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.

Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.

Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.

Эту закономерность можно описать следующей формулой:

Сопротивление

R = ρ l/S

R — сопротивление [Ом]

l — длина проводника [м]

S — площадь поперечного сечения [мм^2]

ρ — удельное сопротивление [Ом*мм^2/м]

Единица измерения сопротивления — Ом. Названа в честь физика Георга Ома.

Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм^2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм^2. При умножении мм^2 сокращаются и мы получаем величину в СИ.

Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм^2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм^2.

• Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.

Видео:Статград по физике 23 января 2024. Тренировочный вариант 3 (ФИ2310301). Полный разборСкачать

Таблица удельных сопротивлений различных материалов

Константан ( сплав Ni-Cu + Mn)

Манганин (сплав меди марганца и никеля — приборный)

Нейзильбер (сплав меди цинка и никеля)

Никелин ( сплав меди и никеля)

Нихром ( сплав никеля хрома железы и марганца)

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Резистор

Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.

Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.

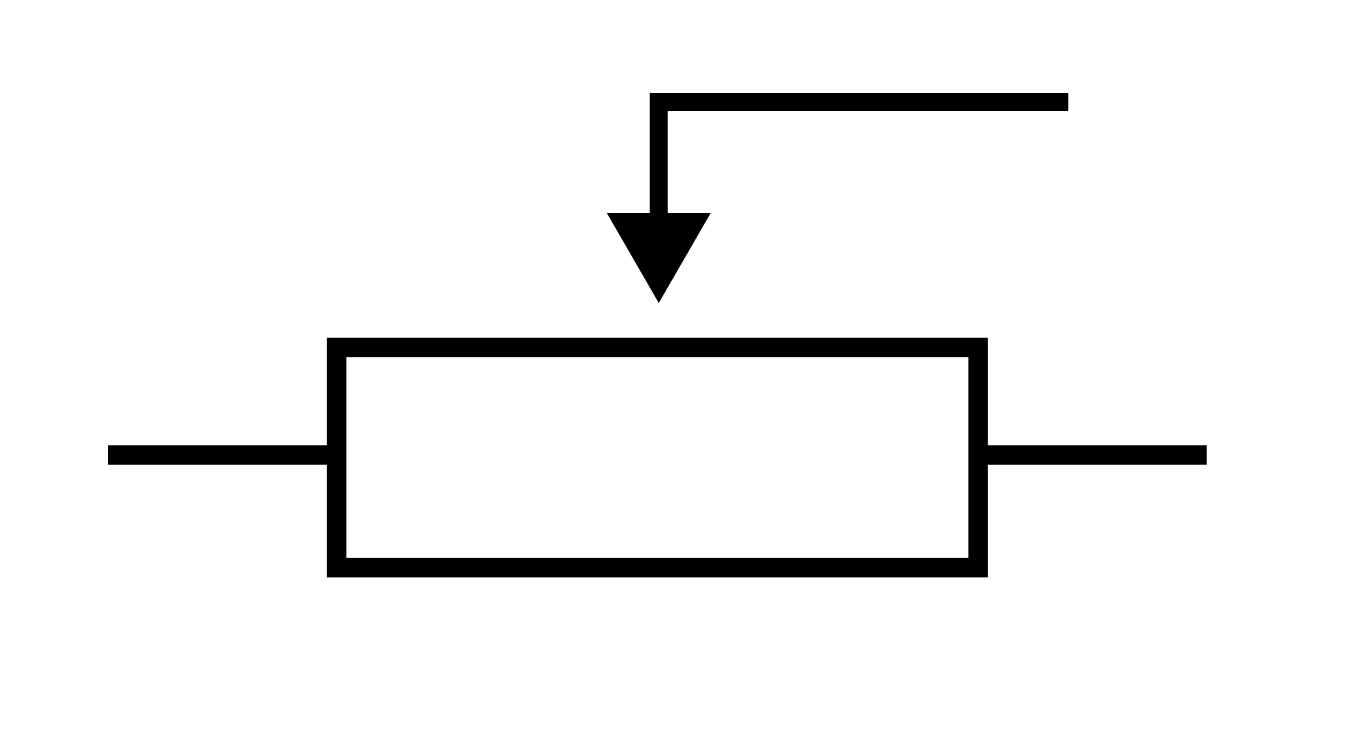
Вот так резистор изображается на схемах:

В школьном курсе физики используют Европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.

Вот так резистор выглядит в естественной среде обитания:

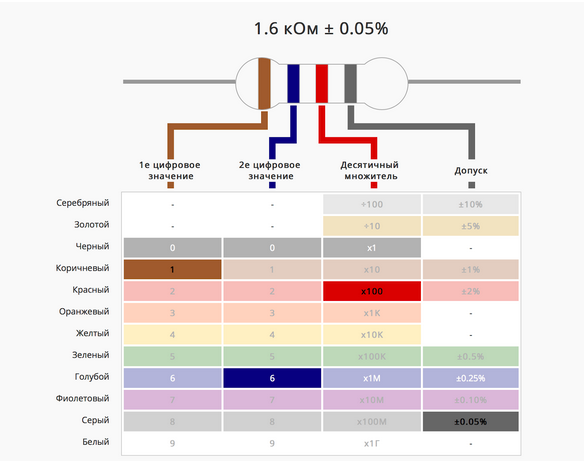
Полосочки на нем показывают его сопротивление.

На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:

О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.

Видео:Длина дуги окружности. 9 класс.Скачать

Реостат

Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.

Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.

По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:

Сопротивление

R = ρ l/S

R — сопротивление [Ом]

l — длина проводника [м]

S — площадь поперечного сечения [мм^2]

ρ — удельное сопротивление [Ом*мм^2/м]

Видео:Задача на расчет эквивалентного сопротивления цепиСкачать

Закон Ома для участка цепи

С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.

Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. Эти реакции выделяют энергию, которая потом передается электрической цепи.

У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «-».

У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.

Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.

Математически его можно описать вот так:

Закон Ома для участка цепи

I = U/R

U — напряжение [В]

R — сопротивление [Ом]

Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.

Сила тока измеряется в Амперах, а подробнее о ней вы можете прочитать в нашей статье 😇

Давайте решим несколько задач на Закон Ома для участка цепи.

Задача раз

Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.

Решение:

Возьмем закон Ома для участка цепи:

I = 220/880 = 0,25 А

Ответ: сила тока, проходящего через лампочку, равна 0,25 А

Давайте усложним задачу. И найдем силу тока, знаю все параметры для вычисления сопротивления и напряжение.

Задача два

Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм^2, а удельное сопротивление нити равно 1,05 Ом*мм^2/м.

Решение:

Сначала найдем сопротивление проводника.

Площадь дана в мм^2, а удельное сопротивления тоже содержит мм^2 в размерности.

Это значит, что можно подставлять значения без перевода в СИ:

R = 1,05*0,5/0,01 = 52,5 Ом

Теперь возьмем закон Ома для участка цепи:

I = 220/52,5 ≃ 4,2 А

Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А

А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.

Задача три

Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм^2, а сила тока в цепи — 8,8 А

Решение:

Возьмем закон Ома для участка цепи и выразим из него сопротивление:

Подставим значения и найдем сопротивление нити:

R = 220/8,8 = 25 Ом

Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:

Подставим значения и получим:

ρ = 25*0,01/0,5 = 0,5 Ом*мм^2/м

Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.

Видео:Быстро и легко определяем центр любой окружностиСкачать

Таблица удельных сопротивлений различных материалов

Константан ( сплав Ni-Cu + Mn)

Манганин (сплав меди марганца и никеля — приборный)

Нейзильбер (сплав меди цинка и никеля)

Никелин ( сплав меди и никеля)

Нихром ( сплав никеля хрома железы и марганца)

Ответ: нить накаливания сделана из константана.

Видео:Длина окружности. Математика 6 класс.Скачать

Закон Ома для полной цепи

Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.

В таком случае вводится Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.

Так, стоп. Слишком много незнакомых слов — разбираемся по-порядку.

Видео:Длина окружности. 9 класс.Скачать

Что такое ЭДС и откуда она берется

ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.

• ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.

Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.

Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.

В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:

Закон Ома для полной цепи

I = ε/(R + r)

R — сопротивление [Ом]

r — внутреннее сопротивление источника [Ом]

Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.

Решим задачу на полную цепь.

Задачка

Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом

Решение:

Возьмем закон Ома для полной цепи:

Ответ: сила тока в цепи равна 1 А.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

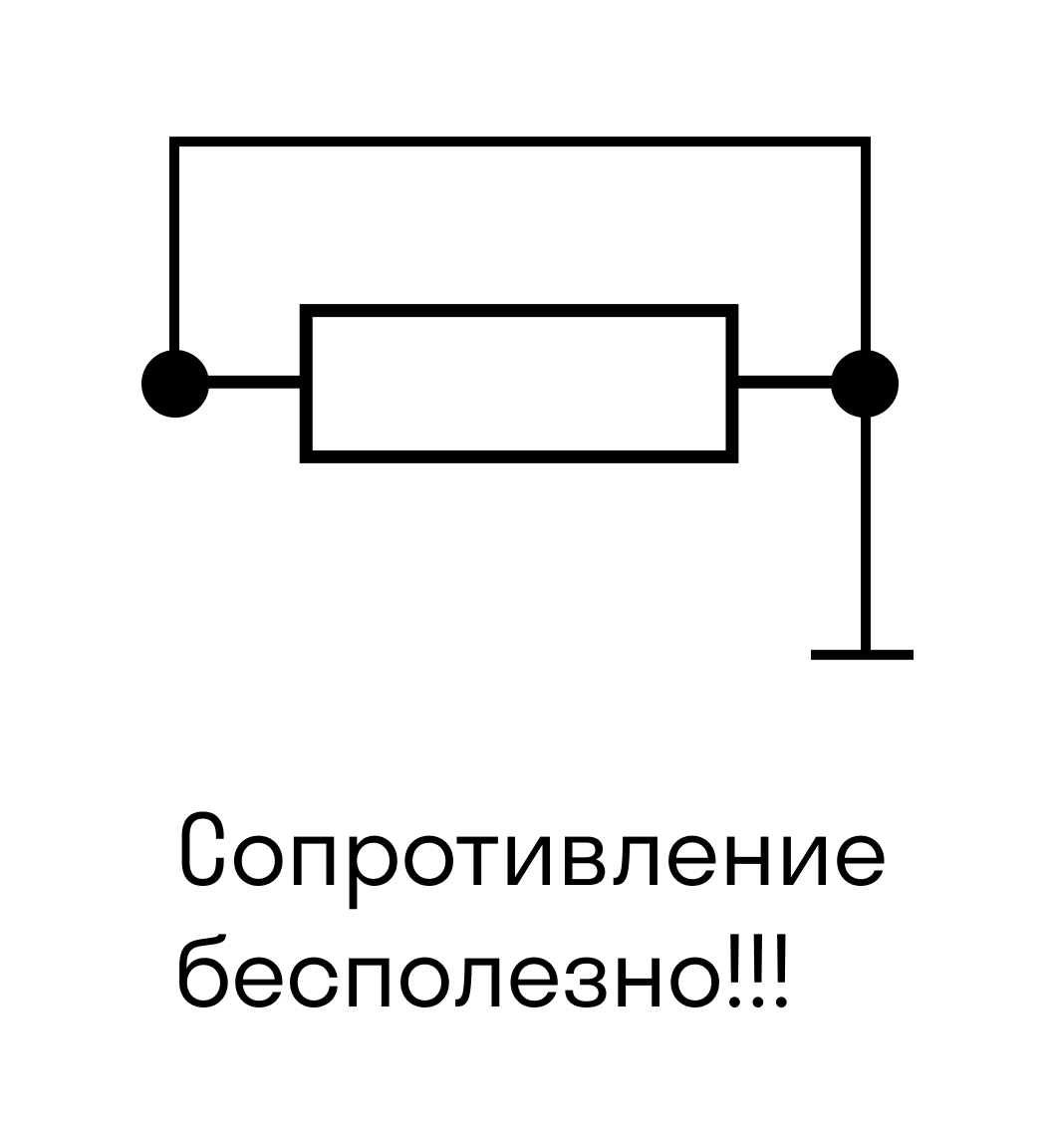
Когда «сопротивление бесполезно»

Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.

А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.

Ток идет по пути наименьшего сопротивления.

Теперь давайте посмотрим на закон Ома для участка цепи еще раз.

Закон Ома для участка цепи

I = U/R

U — напряжение [В]

R — сопротивление [Ом]

Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.

Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.

Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.

Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.

Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Параллельное и последовательное соединение

Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.

Резисторы следуют друг за другом

Между резисторами есть два узла

Узел — это соединение трех и более проводников

Сила тока одинакова на всех резисторах

Сила тока, входящего в узел, равна сумме сил токов, выходящих из него

Общее напряжение цепи складывается из напряжений на каждом резисторе

Напряжение одинаково на всех резисторах

Общее сопротивление цепи складывается из сопротивлений каждого резистора

Общее сопротивление для бесконечного количества параллельно соединенных резисторов

1/R = 1/R1 + 1/R2 + … + 1/Rn

Общее сопротивление для двух параллельно соединенных резисторов

R = (R1 * R2)/R1 + R2

Общее сопротивление бесконечного количества параллельно соединенных одинаковых резисторов

Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала?

Начнем с того, что все электронные компоненты изготавливаются по ГОСТу. То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов.

Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой.

Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного.

Решим несколько задач на последовательное и параллельное соединение.

Задачка раз

Найти общее сопротивление цепи.

R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.

Решение:

Общее сопротивление при последовательном соединении рассчитывается по формуле:

R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом

Ответ: общее сопротивление цепи равно 10 Ом

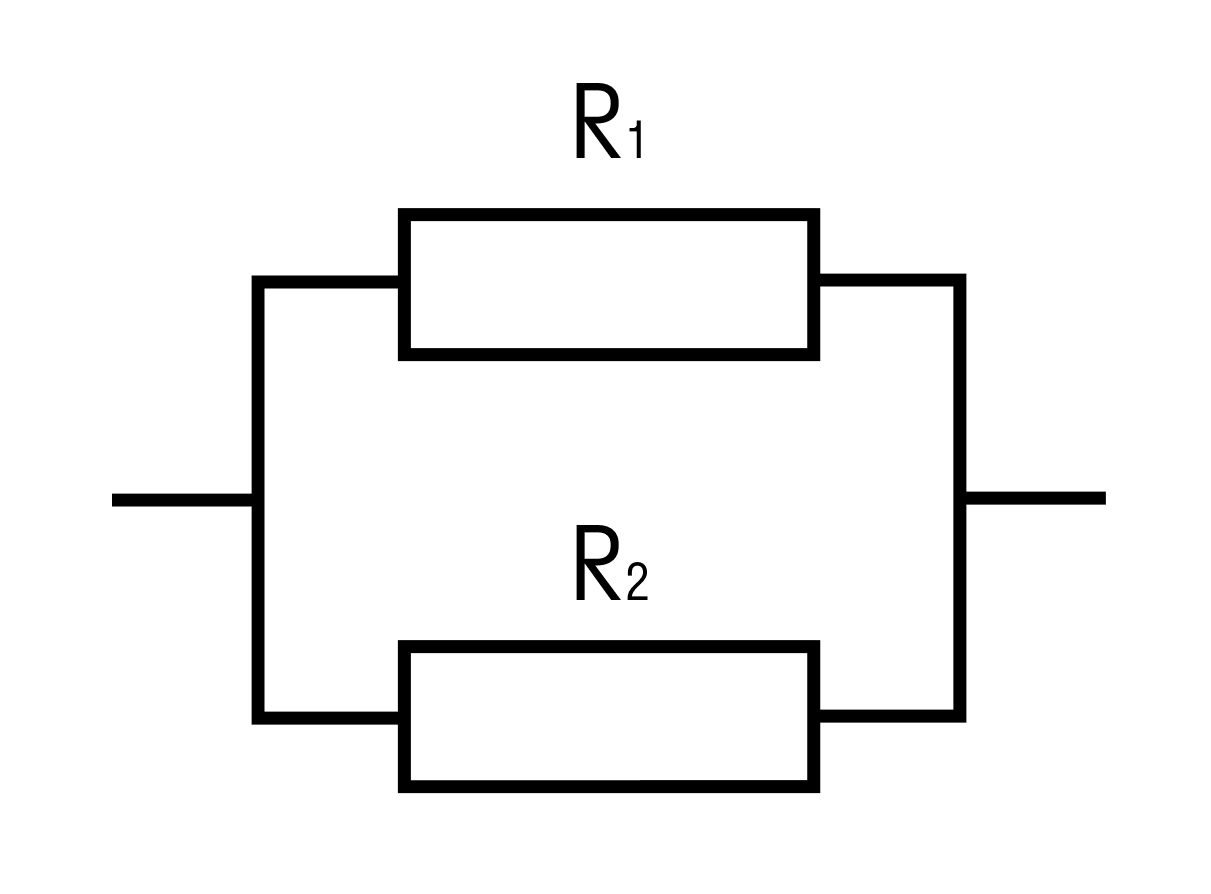
Задачка два

Найти общее сопротивление цепи.

R1 = 4 Ом, R2 = 2 Ом

Решение:

Общее сопротивление при параллельном соединении рассчитывается по формуле:

R = (R1 * R2)/R1 + R2 = 4*2/4+2 = 4/3 = 1 ⅓ Ом

Ответ: общее сопротивление цепи равно 1 ⅓ Ом

Задачка три

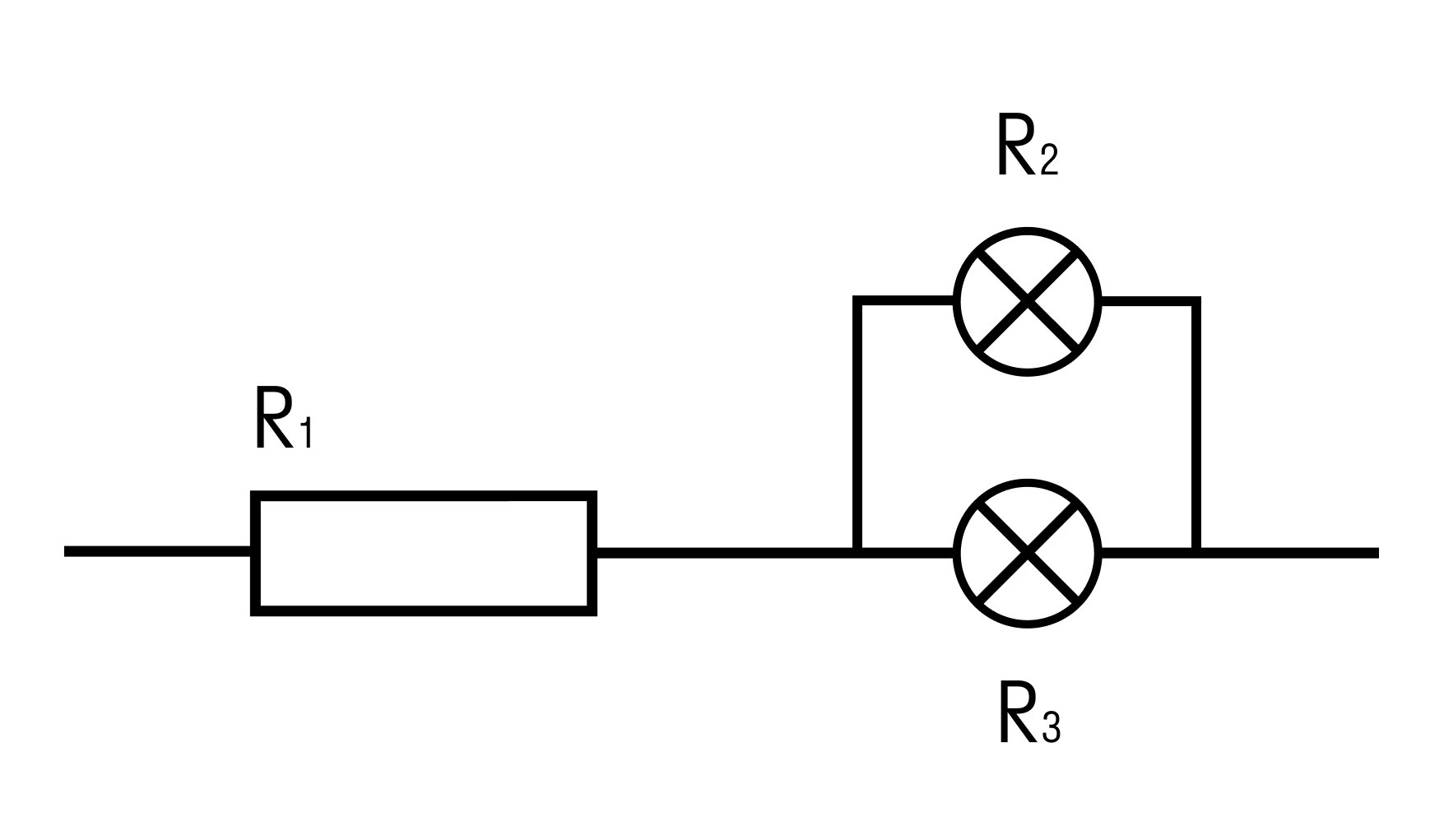
Найти общее сопротивление цепи, состоящей из резистора и двух ламп.

R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом

Решение:

Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.

В данном случае соединение является смешанным. Лампы соеденены параллельно, а последовательно к ним подключен резистор.

Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:

Rламп = (R2 * R3)/R2 + R3 = 2*3/2+3 = 6/5 = 1,2 Ом

Общее сопротивление при последовательном соединении рассчитывается по формуле:

R = R1 + Rламп = 1 + 1,2 = 2,2 Ом

Ответ: общее сопротивление цепи равно 2,2 Ом.

Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи 💪.

Задачка четыре со звездочкой

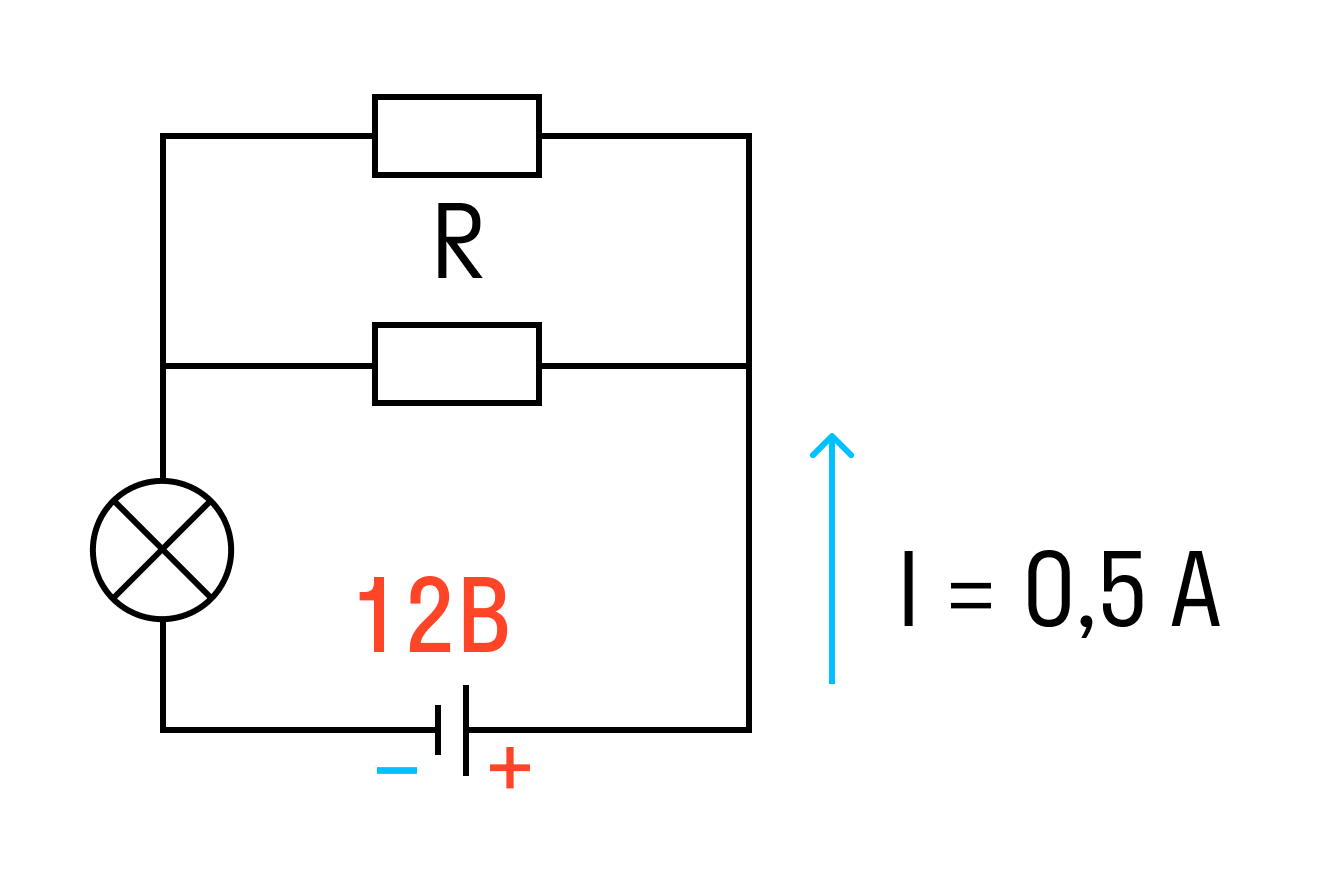
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.

Решение:

Найдем сначала сопротивление лампы.

Rлампы = R/2 = 10/2 = 5 Ом

Теперь найдем общее сопротивление двух параллельно соединенных резисторов.

Rрезисторов = (R * R)/R + R = R^2)/2R = R/2 = 10/2 = 5 Ом

И общее сопротивление цепи равно:

R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом

Выразим внутреннее сопротивление источника из закона Ома для полной цепи.

r = 12/0,5 — 10 = 14 Ом

Ответ: внутреннее сопротивление источника равно 14 Ом.

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!