Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
Видео:Нахождение точки, симметричной данной относительно плоскости в пространствеСкачать

Осевая и центральная симметрия
О чем эта статья:
Видео:Поступающим в магистратуру МГУ, математика, 2018 год, первая волна, задача 1 (1)Скачать

Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Видео:Как найти точку, симметричную точке А(3;4) относительно начала координат. Как решать. Простой способСкачать

Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Видео:Построение симметричной точки относительно плоскости Н или VСкачать

Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Видео:№421. Даны точки А, В и М. Постройте точку, симметричную точке М относительноСкачать

Дробно-линейные отображения


Дробно-линейной функцией называется функция вида: 


Перечислим без доказательства свойства дробно-линейной функции.
- Дробно-линейная функция осуществляет взаимно однозначное отображение расширенной комплексной плоскости на себя. При этом точка
отображается в точку
, а точка
отображается в
.
- Дробно-линейное отображение можно представить в виде суперпозиции трех простейших отображений: целого линейного
, отображения
и сдвига
.
- Дробно-линейное отображение отображает окружности и прямые в окружности и прямые. При этом прямая может перейти как в прямую, так и в окружность. Окружность тоже может перейти как в прямую, так и в окружность. Это свойство называется круговым свойством дробно-линейных отображений.
- Точки симметричные относительно прямой или окружности переходят в точки симметричные относительно образа этой прямой или окружности.
- Дробно-линейное отображение, переводящее три заданные точки в три заданные точки:
дается формулой:
Пример 1 Найти образ мнимой оси при отображении
.
Мнимая ось представляет собой прямую. По третьему свойству она должна перейти в окружность или в прямую. Найдем образы трех точек мнимой оси: 



Пример 2 Найти дробно линейное отображение, переводящее точки
.
Пример 3 Найти образ области
при отображении
Найдем образ мнимой оси при данном отображении. Возьмем три точки : 
Отметим также, что 









Найдем образ точки 
Итак, образ луча 

Теперь мы можем изобразить схему самого отображения:
Пример 4 Найти образы всех квадрантов при отображении .
Чтобы не решать опять задачи подобные примеру 3, воспользуемся следствием принципа симметрии Римана-Шварца в такой формулировке:
Пусть функция 







Пусть 











На следующем рисунке видно, что области 




Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.


Нужна помощь с курсовой или дипломной работой?
🔥 Видео
Осевая симметрия. 6 класс.Скачать

Как найти точку, симметричную точке А(-2;3) относительно биссектрисы первого координатного углаСкачать

Симметрия относительно точки. 6 классСкачать

Симметрия относительно прямойСкачать

Центральная симметрия. 6 класс.Скачать

Как искать точки на тригонометрической окружности.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Точка встречи прямой с плоскостьюСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

ВПР 6 класс. 12 задание. Фигура симметиичная данной относительно оси.Скачать

№416. Даны две точки А и В, симметричные относительно некоторой прямой, и точка М.Скачать

Геометрия 8 класс (Урок№7 - Осевая и центральная симметрия.)Скачать

Симметрия относительно точки, линии. Математика 6 класс. Подготовка к ЕГЭ, ОГЭ, ЦТ, экзаменуСкачать

Осевая и центральная симметрия, 6 классСкачать

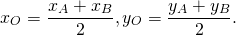
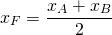
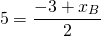
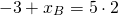
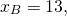
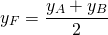
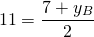
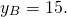
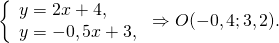
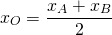
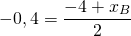
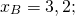
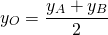
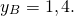













 отображается в точку
отображается в точку  , а точка
, а точка  отображается в
отображается в  , отображения
, отображения  и сдвига
и сдвига  .
. дается формулой:
дается формулой: 
 .
. .
.
 при отображении
при отображении 





