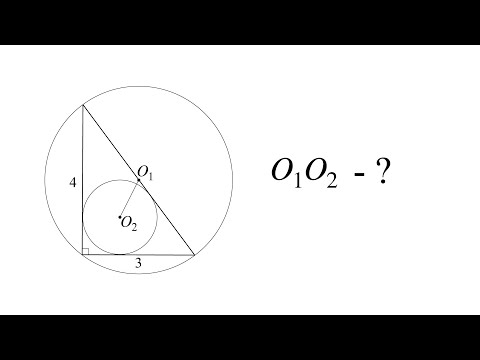Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Как найти расстояние между центрами окружностей
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Ответ
- Проверено экспертом
- Всё про окружность и круг
- 🌟 Видео
Видео:Расстояние между центрами. Окружность. Математика 10-11 классы.Скачать

Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
 | ||
| Внешнее касание двух окружностей | ||
 | ||
| Внутреннее касание двух окружностей | ||
 | ||
| Окружности пересекаются в двух точках | ||
 | ||
 | ||
| Каждая из окружностей лежит вне другой | ||
 Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
 Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутренняя касательная к двум окружностям | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутреннее касание двух окружностей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружности пересекаются в двух точках | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешнее касание двух окружностей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Каждая из окружностей лежит вне другой | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Формула | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешняя касательная к двум окружностям |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутренняя касательная к двум окружностям |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Общая хорда двух пересекающихся окружностей |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешняя касательная к двум окружностям | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Общая хорда двух пересекающихся окружностей | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешняя касательная к двум окружностям | |||||||||
| Внутренняя касательная к двум окружностям | |||||||||
| Общая хорда двух пересекающихся окружностей | |||||||||
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Как найти расстояние между центрами | Олимпиадная математикаСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Сможешь найти расстояние между центрами пересекающихся окружностей?Скачать 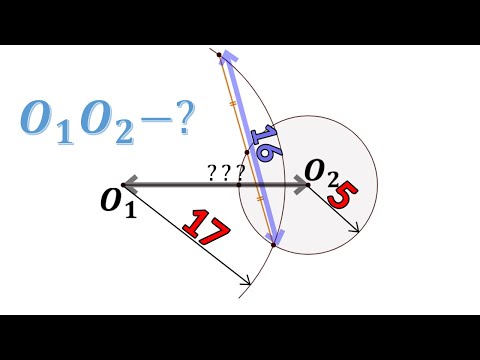 Как найти расстояние между центрами окружностейУ Вас недостаточно прав для добавления комментариев. Все права защищены 2019
Видео:Планиметрия 11 |mathus.ru| расстояние между центрами пересекающихся окружностейСкачать  Взаимное расположение двух окружностей
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей | |||||||||
| Каждая из окружностей лежит вне другой |  | ||||||||
| Внешнее касание двух окружностей |  | ||||||||
| Внутреннее касание двух окружностей |  | ||||||||
| Окружности пересекаются в двух точках |  |  | |||||||
| Каждая из окружностей лежит вне другой | |||||||||
 | |||||||||
| Внешнее касание двух окружностей | |||||||||
 | |||||||||
| Внутреннее касание двух окружностей | |||||||||
 | |||||||||
| Окружности пересекаются в двух точках | |||||||||
 | |||||||||
 | |||||||||
| Каждая из окружностей лежит вне другой | |||||||||
 Расстояние между центрами окружностей больше суммы их радиусов | |||||||||
| Внешнее касание двух окружностей | |||||||||
 Расстояние между центрами окружностей равно сумме их радиусов | |||||||||
| Внутреннее касание двух окружностей | |||||||||
| Окружности пересекаются в двух точках | |||||||||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов Расстояние между центрами окружностей меньше разности их радиусов d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой. | |||||||||
| Внутренняя касательная к двум окружностям |  | ||||||||
| Внутреннее касание двух окружностей |  | ||||||||
| Окружности пересекаются в двух точках |  | ||||||||
| Внешнее касание двух окружностей |  | ||||||||
 | |||||||||
 | |||||||||
| Внешняя касательная к двум окружностям | |
 | |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Внутреннее касание двух окружностей |
| Окружности пересекаются в двух точках |
| Внешнее касание двух окружностей |
| Каждая из окружностей лежит вне другой |
| Фигура | Рисунок | Формула | ||
| Внешняя касательная к двум окружностям |  | |||
| Внутренняя касательная к двум окружностям |  | |||
| Общая хорда двух пересекающихся окружностей |  | |||
| Внешняя касательная к двум окружностям | |
 | |
Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Планиметрия 12 | mathus.ru | расстояние между центрами пересекающихся окружностейСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Планиметрия 5 | mathus.ru | расстояние между центрами окружностей в параллелограммеСкачать  ОтветПроверено экспертомУравнение окружности с центром (a;b) и радиусом R центр окружности (-2;6) радиус 6 центр окружности (4;-5)радиус 5 по формуле расстояние между двумя точками : находим расстояние между центрами заданных окружностей Видео:✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать  Всё про окружность и кругОкружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R). Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр. Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R. Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2 Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания. Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC. Квадрат касательной равен произведению секущей на ее внешнюю часть Центральный угол — это угол, вершина которого совпадает с центром окружности. Дугой называется часть окружности, заключенная между двумя точками. Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу. Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее. Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности. Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы. Периметр сектора: P = s + 2R. Площадь сектора: S = Rs/2 = ПR 2 а/360°. Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой. 🌟 ВидеоРасстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать  Найти центр и радиус окружностиСкачать  Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать  М1152. Расстояние между центрами вписанной и описанной окружностейСкачать  Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать  1 2 4 сопряжение окружностейСкачать  9 класс, 8 урок, Взаимное расположение двух окружностейСкачать  Длина отрезкаСкачать  как измерить межцентровое расстояние между отверстиями обычным штангельциркулем?Скачать  Расстояние между точкамиСкачать  Уравнение окружности и формула расстояния между точками на плоскостиСкачать  |