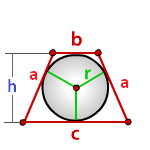
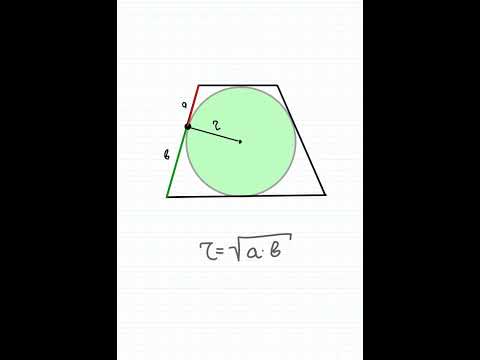
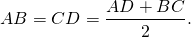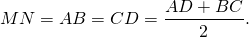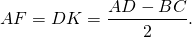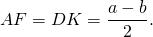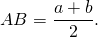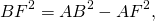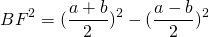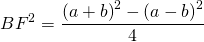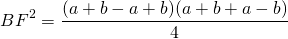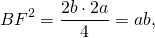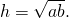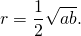с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
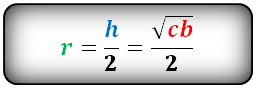
Формула радиуса вписанной окружности равнобочной трапеции ( r ):
Калькулятор — вычислить, найти радиус вписанной окружности в равнобочную трапецию
Радиус вписанной окружности в трапецию, формула
Радиус вписанной окружности в трапецию равен половине высоты трапеции.
Главное чтобы выполнялось условие при котором в данную трапецию возможно вписать окружность. В четырехугольник окружность можно вписать только в том случае, если суммы его противоположных сторон равны. т.е.:
Иначе в данную трапецию нельзя вписать окружность.
бедро трапеции выражается через высоту по теореме Пифагора:
Отсюда — зная все стороны трапеции вычислим такую высоту трапеции, которая удовлетворяет условию вписанной окружности (3).
после небольших преобразований получим
используем формулы Квадрат суммы и Квадрат разности и после раскрытия скобок и упрощения получим
И соответственно радиус вписанной окружности в трапецию
Вписанная в равнобедренную трапецию окружность
Какими свойствами обладает вписанная в равнобедренную трапецию окружность?
1. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин её противоположных сторон равны.
То есть, в трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
И обратно, если для трапеции ABCD верно равенство AD+BC=AB+CD, то в неё можно вписать окружность.
Таким образом, если трапеция ABCD — равнобедренная, AD||BC, то её боковые стороны равны полусумме оснований:
2. Отсюда, по свойству средней линии трапеции, боковые стороны равнобедренной трапеции, в которую можно вписать окружность, равны её средней линии.
Если MN —
3. Высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями.
По свойству равнобедренной трапеции,
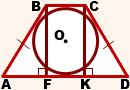
Из прямоугольного треугольника ABF по теореме Пифагора
4. Так как радиус вписанной в трапецию окружности равен половине высоты трапеции, то для равнобедренной трапеции верно равенство
5. В равнобедренной трапеции точки касания делят стороны на две группы равных отрезков.
6. Центр вписанной в равнобедренную трапецию окружности — точка пересечения её биссектрис.
Таким образом, в трапеции ABCD, AD||BC, CO и DO — биссектрисы углов ADC и BCD,