Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
R — радиус окружности (круга)
D — диаметр, D = 2 R
Формула для определения длины радиуса, если известна площадь круга :
- Калькулятор для расчета длины радиуса через площадь
- Калькулятор для расчета длины радиуса через длину окружности
- Радиус — что это такое и как найти радиус окружности
- Через длину стороны
- Найти радиус круга, зная окружность
- Радиус и диаметр
- Вычисление радиуса
- Если известен диаметр
- Если известна длина окружности круга
- Если известна площадь круга
- Способ расчета радиуса круга:
- Через сторону описанного квадрата
- Как посчитать радиус зная длину окружности
- Формула
- Свойства радиуса
- По площади сектора и центральному углу
- Площадь сегмента
- Формулы для площади круга и его частей
- Центральный угол, вписанный угол и их свойства
- Связанные определения
- Примеры задач
- Длина дуги
- Уравнение окружности
- Углы между двумя хордами
- Через площадь и полупериметр описанного треугольника
- Основные свойства касательных к окружности
- Обобщения
- Через диагональ вписанного прямоугольника
- Площадь круга, онлайн расчет
- Вместо заключения
- Как зная хорду вычислить радиус окружности
- Все основные формулы для определения длины радиуса окружности
- Калькулятор для расчета длины радиуса через площадь
- Калькулятор для расчета длины радиуса через длину окружности
- Сегмент круга
- Формулы вычисления параметров сегмента
- Геометрия круга
Калькулятор для расчета длины радиуса через площадь
Формула для определения длины радиуса, если известна длина окружности :
Калькулятор для расчета длины радиуса через длину окружности
R — радиус окружности (круга)
h — высота сегмента
α — центральный угол
Формула для определения длины радиуса, если известна длина хорды :
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Радиус — что это такое и как найти радиус окружности
Видео:Вписанный угол, опирающийся на хорду, равную радиусу окружностиСкачать

Через длину стороны
Формула для нахождения длины окружности через радиус:
, где r — радиус окружности.
Видео:Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Найти радиус круга, зная окружность
 |  |
Видео:Радиус и диаметрСкачать

Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
Длина диаметра равна удвоенной длине радиуса.
Видео:ЕГЭ-2022 ||Задание №6 || Найти длину хордыСкачать

Вычисление радиуса
Радиус можно посчитать разными способами.
Если известен диаметр
Этот способ самый простой. Диаметр равен двум радиусам. Поэтому радиус будет высчитываться по формуле r=d/2.
Если известна длина окружности круга
Также несложно будет узнать радиус, если известна длина окружности круга. Формула для расчета длины окружности C=2πr, в которой C является длиной окружности, π=3,14, а r — это как раз искомый радиус.
Преобразовав данную формулу, получим: r=C/2π. Вообще, число «Пи» в формуле — это постоянное значение, округленное до 3,14. На самом деле «Пи» выглядит так:
Означает данное значение отношение длины окружности к диаметру той же окружности.
Если известна площадь круга
Формула площади круга выглядит так: A= π(r²). Эту формулу можно преобразовать в формулу радиуса:
В ней A — это площадь круга, число «Пи» мы уже знаем, оно равно округленно 3,14, а r — это и есть искомое значение радиуса.
Как найти радиус круга, все школьники учат на геометрии. Взрослые, конечно, со временем забывают эти формулы. Но, прочитав данную статью, радиус круга может найти каждый: и взрослый, и ребенок.
Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать

Способ расчета радиуса круга:
Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где P – длина окружности, pi – число π, равное примерно 3.14
Круг (окружность) – геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центр круга).
Формула радиуса круга:
где S – площадь круга, pi – число π, равное примерно 3.14
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Через сторону описанного квадрата
Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.
- r — искомый радиус окружности.
- a — сторона описанного квадрата.
Как посчитать радиус зная длину окружности
Чему равен радиус (r) если длина окружности C?
Формула
r = C /2π , где π ≈ 3.14
Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Свойства радиуса
В отношении радиуса действуют несколько важных правил:
- Радиус составляет половину диаметра. Это мы продемонстрировали только что.
- У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.
Радиус, который перпендикулярен хорде, делит ее на две равные части.
Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

По площади сектора и центральному углу
- Например, если площадь сектора равна 50 см 2 , а центральный угол равен 120 градусов, формула запишется следующим образом: .
Видео:Как найти радиус окружности, зная три отрезка | Денис ЖучковСкачать

Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла .
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах , получаем
В случае, когда величина α выражена в в радианах , получаем
Видео:Найти радиус окружности если известны длины пересекающихся хордСкачать
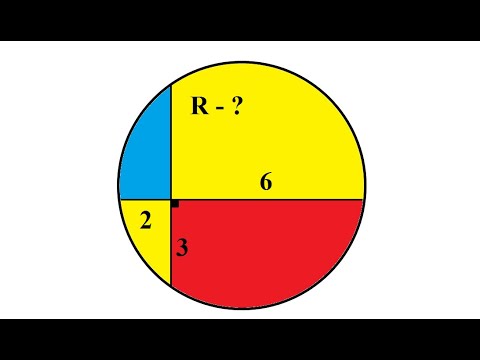
Формулы для площади круга и его частей
| Числовая характеристика | Рисунок | Формула | |
| Площадь круга |  | ||
| Площадь сектора |  | ||
| Площадь сегмента |  | ||
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга


если величина угла α выражена в радианах

если величина угла α выражена в градусах


если величина угла α выражена в радианах

если величина угла α выражена в градусах
Видео:Радиус описанной окружностиСкачать

Центральный угол, вписанный угол и их свойства
Видео:ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать

Связанные определения
- Центральный угол в окружности — это угол , образованный двумя радиусами.
- Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.
Видео:Длина окружности. Математика 6 класс.Скачать

Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла .
В случае, когда величина α выражена в градусах , справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах , справедлива пропорция
из которой вытекает равенство:
Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Уравнение окружности
r 2 = ( x – a ) 2 + ( y – b ) 2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:
| < | x = a + r cos t |
| y = b + r sin t |
Видео:Всё про вписанные и центральные углы за 4 минуты | Борис Трушин |Скачать

Углы между двумя хордами
Случай 1: два секущие пересекаются внутри окружности.
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны Случай 2: две секущие пересекаются вне окружности.
Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.
Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Через площадь и полупериметр описанного треугольника
Разделите площадь описанного треугольника на его полупериметр.
- r — искомый радиус окружности.
- S — площадь треугольника.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Видео:Длина дуги окружности. 9 класс.Скачать

Основные свойства касательных к окружности
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
Видео:Радиус Хорда ДиаметрСкачать

Обобщения
Радиусом множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, радиус n-размерного гиперкуба со стороной s равен
Через диагональ вписанного прямоугольника
Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.
- R — искомый радиус окружности.
- d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
- a, b — стороны вписанного прямоугольника.
Площадь круга, онлайн расчет
Вместо заключения
Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.
Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.
Как зная хорду вычислить радиус окружности
Все основные формулы для определения длины радиуса окружности
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
R — радиус окружности (круга)
D — диаметр, D = 2 R
Формула для определения длины радиуса, если известна площадь круга :
Калькулятор для расчета длины радиуса через площадь
Формула для определения длины радиуса, если известна длина окружности :
Калькулятор для расчета длины радиуса через длину окружности
R — радиус окружности (круга)
h — высота сегмента
α — центральный угол
Формула для определения длины радиуса, если известна длина хорды :
Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента — по углу, по хорде, по радиусу, по высоте и длине дуги.

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
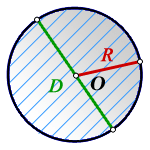
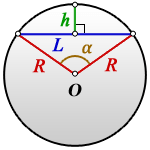
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Геометрия круга
Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии.
Давайте сначала рассмотрим, какие у круга бывают части и как они называются.
- Окружность — линия, ограничивающая круг.
- Дуга — часть окружности.
- Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
- Хорда — отрезок, соединяющий две точки окружности.
- Сегмент — часть круга, ограниченная хордой и дугой.
- Сектор — часть круга, ограниченная двумя радиусами и дугой.
Интересующие нас величины и их обозначения:
- R — радиус круга (здесь «радиус» — это уже не отрезок, а его длина);
- D — диаметр круга — двойной радиус;
- C — длина окружности;
- L — длина дуги;
- X — длина хорды;
- H — высота сегмента;
- φ — центральный угол — угол между двумя радиусами;
— площадь круга;
— площадь сектора;
— площадь сегмента.
Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.
- Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
- Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
- Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.
Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.
Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).
И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.
И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.
1. Даны диаметр D и длина дуги L


высота сегмента 

2. Даны диаметр D и длина хорды X


высота сегмента 

Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол 
3. Даны диаметр D и центральный угол φ


длина хорды 

4. Даны диаметр D и высота сегмента H


длина хорды 

6. Даны длина дуги L и центральный угол φ


длина хорды 

8. Даны длина хорды X и центральный угол φ


диаметр 

9. Даны длина хорды X и высота сегмента H


диаметр 

10. Даны центральный угол φ и высота сегмента H


длина дуги 

Внимательный читатель не мог не заметить, что я пропустил два варианта:
5. Даны длина дуги L и длина хорды X
7. Даны длина дуги L и высота сегмента H
Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?
Задача эта сводится к решению уравнений: 

и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.
Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:
длина окружности 
площадь круга 
площадь сектора 
площадь сегмента 
И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.
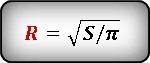
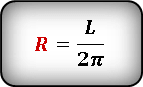








































 — площадь круга;
— площадь круга; — площадь сектора;
— площадь сектора; — площадь сегмента.
— площадь сегмента.