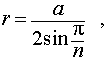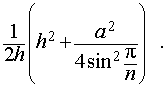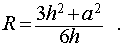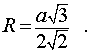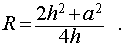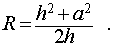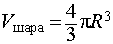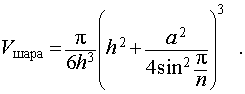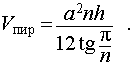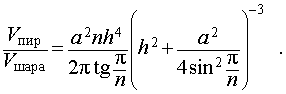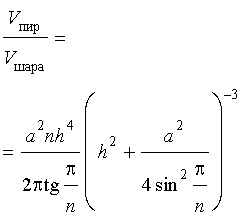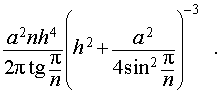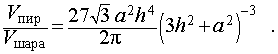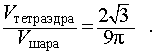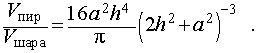Как найти радиус окружности описанной около пирамиды

В данной публикации представлены формулы, с помощью которых можно найти радиус сферы (шара), описанной около правильной пирамиды: треугольной, четырехугольной, шестиугольной и тетраэдра.

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Формулы расчета радиуса сферы (шара)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На этом рисунке и чертежах далее:

• a – ребро основания пирамиды;
• h – высота фигуры.

Если эти величины даны, вычислить радиус (R) описанной вокруг пирамиды сферы/шара можно по формуле ниже:

Правильный тетраэдр является разновидностью правильной треугольной пирамиды. Формула для него:

Правильная четырехугольная пирамида

Радиус (R) описанной сферы/шара вычисляется следующим образом:

Правильная шестиугольная пирамида

Формула для нахождения радиус (R) сферы/шара выглядит так:

Видео:Радиус описанной окружностиСкачать

Пирамида, вписанная в сферу

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

Радиус сферы, описанной около правильной n — угольной пирамиды

Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

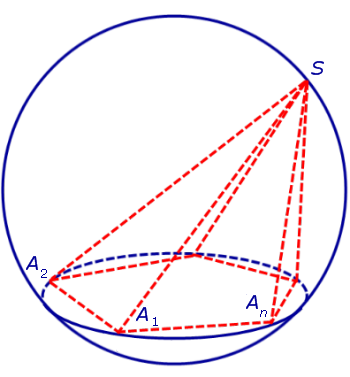
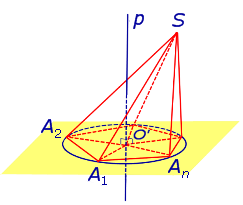
Определение 1. Пирамидой, вписанной в сферу, называют такую пирамиду, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если пирамида вписана в сферу, то сферу называют описанной около пирамиды.

Теорема 1. Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.

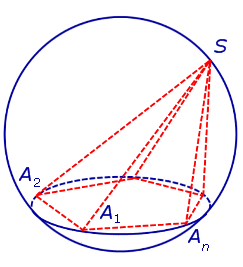
Доказательство. Докажем сначала, что, если пирамида вписана в сферу, то около ее основания можно описать окружность. Для этого рассмотрим рисунок 2.

На рисунке 2 изображена пирамида SA₁A₂ . A_n , вписанная в сферу. Плоскость основания пирамиды пересекает сферу по окружности, в которую вписан многоугольник A₁A₂ . A_n – основание пирамиды. Доказано.

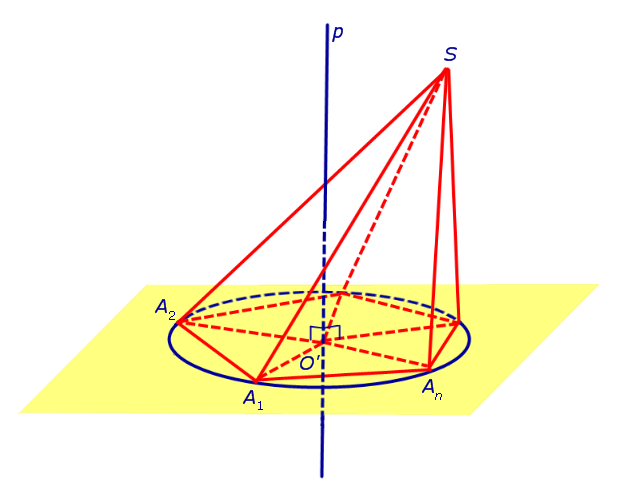
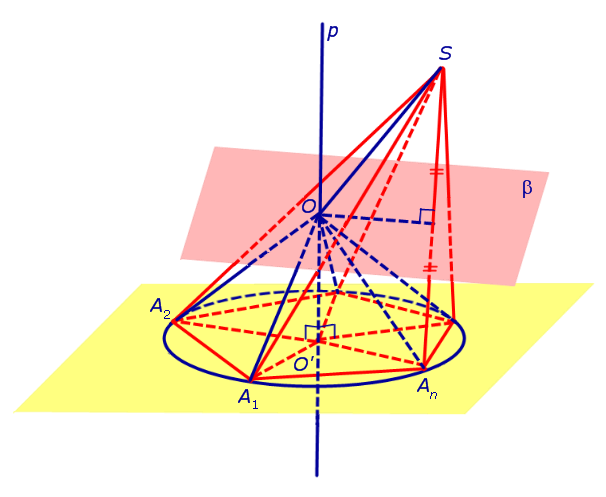
Теперь предположим, что около основания A₁A₂ . A_n пирамиды SA₁A₂ . A_n можно описать окружность. Докажем, что в этом случае около пирамиды SA₁A₂ . A_n можно описать сферу. С этой целью обозначим центр окружности, описанной около многоугольника A₁A₂ . A_n , символом O’ и проведем прямую p, проходящую через точку O’ и перпендикулярную к плоскости многоугольника A₁A₂ . A_n (рис. 3).

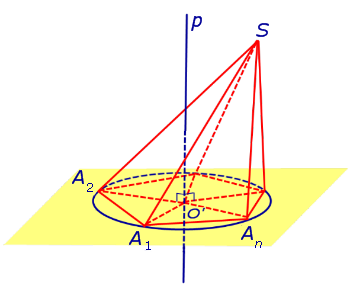
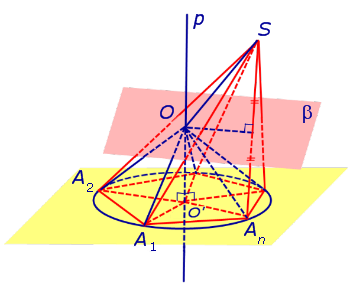
Рассмотрим плоскость β, проходящую через середину отрезка SA_n и перпендикулярную к этому отрезку. Если обозначить буквой O точку пересечения плоскости β с прямой p, то точка O и будет центром сферы, описанной около пирамиды SA₁A₂ . A_n . Для того, чтобы это доказать, рассмотрим следующий рисунок 4.

Итак, мы доказали, что точка O находится на одном и том же расстоянии от всех вершин пирамиды SA₁A₂ . A_n . Отсюда вытекает, что точка O является центром сферы, описанной около пирамиды SA₁A₂ . A_n .

Для завершения доказательства теоремы остается лишь доказать, что плоскость β и прямая p действительно пересекаются. Если предположить, что это не так, то из такого предположения будет следовать, что плоскость β и прямая p параллельны, а, значит, точка S лежит в плоскости A₁A₂ . A_n , что противоречит определению пирамиды.

Следствие 1. Около любой правильной пирамиды можно описать сферу.

Следствие 2. Если у пирамиды все боковые ребра равны, то около нее можно описать сферу.

Указание. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее основания, является центром описанной около основания окружности. Посмотреть доказательство.

Видео:Быстро находим радиус описанной сферыСкачать

Радиус сферы, описанной около правильной n — угольной пирамиды

Задача 1. Высота правильной n — угольной пирамиды равна h , а длина ребра основания равна a . Найти радиус сферы, описанной около пирамиды.

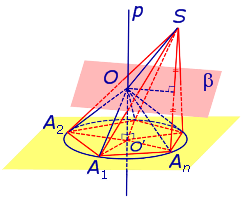
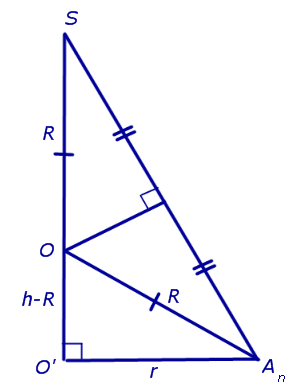
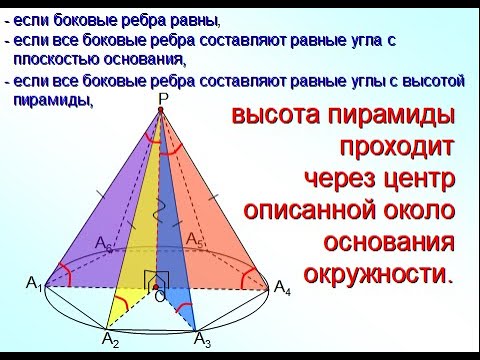
Решение. Рассмотрим правильную n — угольную пирамиду SA₁A₂ . A_n и обозначим буквой O центр описанной около пирамиды сферы, а символом O’ – центр основания пирамиды. Проведем плоскость SO’A_n (рис. 5).

Буквой R на рисунке 5 обозначен радиус описанной около пирамиды сферы, а буквой r – радиус описанной около основания пирамиды окружности. По теореме Пифагора для треугольника O’OA_n получаем

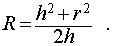(1)

из формулы (1) получаем соотношение

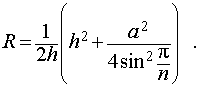(2)

Ответ.

Следствие 3. Радиус сферы, описанной около правильной треугольной пирамиды с высотой h и ребром основания a , равен

Следствие 4. Радиус сферы, описанной около правильного тетраэдра с ребром a , равен

Следствие 5. Радиус сферы, описанной около правильной четырехугольной пирамиды с высотой h и ребром основания a , равен

Следствие 6. Радиус сферы, описанной около правильной шестиугольной пирамиды с высотой h и ребром основания a , равен

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Задача 2. Около правильной n — угольной пирамиды с высотой h и ребром основания a описана сфера. Найти отношение объемов пирамиды и шара, ограниченного сферой, описанной около данной пирамиды.

Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около пирамиды сферой, через высоту и ребро основания пирамиды:

Ответ.

Следствие 7. Отношение объема правильной треугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной пирамиды, равно

Следствие 8. Отношение объема правильного тетраэдр с ребром a к объему шара, ограниченного сферой, описанной около данного тетраэдра, равно

Следствие 9. Отношение объема правильной четырехугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 10. Отношение объема правильной шестиугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Видео:Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать

Радиус окружности описанной около основания правильной

Видео:Геометрия Найдите радиус окружности описанной около равнобедренного треугольника с основанием 16 смСкачать

Нахождение радиуса сферы (шара), описанной около правильной пирамиды

В данной публикации представлены формулы, с помощью которых можно найти радиус сферы (шара), описанной около правильной пирамиды: треугольной, четырехугольной, шестиугольной и тетраэдра.

Видео:Нахождение радиуса сферы, описанной около пирамидыСкачать

Формулы расчета радиуса сферы (шара)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

На этом рисунке и чертежах далее:

• a – ребро основания пирамиды;
• h – высота фигуры.

Если эти величины даны, вычислить радиус (R) описанной вокруг пирамиды сферы/шара можно по формуле ниже:

Правильный тетраэдр является разновидностью правильной треугольной пирамиды. Формула для него:

Правильная четырехугольная пирамида

Радиус (R) описанной сферы/шара вычисляется следующим образом:

Правильная шестиугольная пирамида

Формула для нахождения радиус (R) сферы/шара выглядит так:

Видео:Найти радиус описанной сферы около пирамиды Д213Скачать

Пирамида, вписанная в сферу

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

Радиус сферы, описанной около правильной n — угольной пирамиды

Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Видео:Радиус описанной окружности трапецииСкачать

Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу

Определение 1. Пирамидой, вписанной в сферу, называют такую пирамиду, все вершины которой лежат на сфере (рис. 1).

Определение 2. Если пирамида вписана в сферу, то сферу называют описанной около пирамиды.

Теорема 1. Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.

Доказательство. Докажем сначала, что, если пирамида вписана в сферу, то около ее основания можно описать окружность. Для этого рассмотрим рисунок 2.

На рисунке 2 изображена пирамида SA₁A₂ . A_n , вписанная в сферу. Плоскость основания пирамиды пересекает сферу по окружности, в которую вписан многоугольник A₁A₂ . A_n – основание пирамиды. Доказано.

Теперь предположим, что около основания A₁A₂ . A_n пирамиды SA₁A₂ . A_n можно описать окружность. Докажем, что в этом случае около пирамиды SA₁A₂ . A_n можно описать сферу. С этой целью обозначим центр окружности, описанной около многоугольника A₁A₂ . A_n , символом O’ и проведем прямую p, проходящую через точку O’ и перпендикулярную к плоскости многоугольника A₁A₂ . A_n (рис. 3).

Рассмотрим плоскость β, проходящую через середину отрезка SA_n и перпендикулярную к этому отрезку. Если обозначить буквой O точку пересечения плоскости β с прямой p, то точка O и будет центром сферы, описанной около пирамиды SA₁A₂ . A_n . Для того, чтобы это доказать, рассмотрим следующий рисунок 4.

Итак, мы доказали, что точка O находится на одном и том же расстоянии от всех вершин пирамиды SA₁A₂ . A_n . Отсюда вытекает, что точка O является центром сферы, описанной около пирамиды SA₁A₂ . A_n .

Для завершения доказательства теоремы остается лишь доказать, что плоскость β и прямая p действительно пересекаются. Если предположить, что это не так, то из такого предположения будет следовать, что плоскость β и прямая p параллельны, а, значит, точка S лежит в плоскости A₁A₂ . A_n , что противоречит определению пирамиды.

Следствие 1. Около любой правильной пирамиды можно описать сферу.

Следствие 2. Если у пирамиды все боковые ребра равны, то около нее можно описать сферу.

Указание. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее основания, является центром описанной около основания окружности. Посмотреть доказательство.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Радиус сферы, описанной около правильной n — угольной пирамиды

Задача 1. Высота правильной n — угольной пирамиды равна h , а длина ребра основания равна a . Найти радиус сферы, описанной около пирамиды.

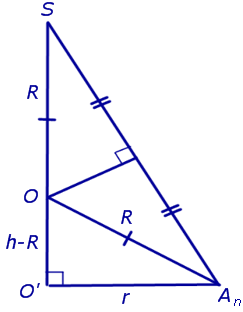
Решение. Рассмотрим правильную n — угольную пирамиду SA₁A₂ . A_n и обозначим буквой O центр описанной около пирамиды сферы, а символом O’ – центр основания пирамиды. Проведем плоскость SO’A_n (рис. 5).

Буквой R на рисунке 5 обозначен радиус описанной около пирамиды сферы, а буквой r – радиус описанной около основания пирамиды окружности. По теореме Пифагора для треугольника O’OA_n получаем

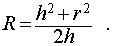(1)

из формулы (1) получаем соотношение

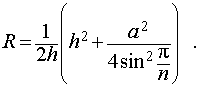(2)

Ответ.

Следствие 3. Радиус сферы, описанной около правильной треугольной пирамиды с высотой h и ребром основания a , равен

Следствие 4. Радиус сферы, описанной около правильного тетраэдра с ребром a , равен

Следствие 5. Радиус сферы, описанной около правильной четырехугольной пирамиды с высотой h и ребром основания a , равен

Следствие 6. Радиус сферы, описанной около правильной шестиугольной пирамиды с высотой h и ребром основания a , равен

Видео:Задача 6 №27921 ЕГЭ по математике. Урок 138Скачать

Отношение объемов правильной n — угольной пирамиды и шара, ограниченного сферой, описанной около данной пирамиды

Задача 2. Около правильной n — угольной пирамиды с высотой h и ребром основания a описана сфера. Найти отношение объемов пирамиды и шара, ограниченного сферой, описанной около данной пирамиды.

Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около пирамиды сферой, через высоту и ребро основания пирамиды:

Ответ.

Следствие 7. Отношение объема правильной треугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной пирамиды, равно

Следствие 8. Отношение объема правильного тетраэдр с ребром a к объему шара, ограниченного сферой, описанной около данного тетраэдра, равно

Следствие 9. Отношение объема правильной четырехугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Следствие 10. Отношение объема правильной шестиугольной пирамиды с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно

Видео:Формулы для радиуса окружности #shortsСкачать

Радиус окружности описанной около основания правильной

Вопрос по геометрии:

радиус окружности, описанной около основания правильной треугольной пирамиды равен 3. Боковое ребро равно 5. Найдите высоту пирамиды.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Полиночка, все на чертеже. Так строится правильная треуголоная пирамида и только так. AO это радиус описанной окружности.SO находим по т.Пифагора SO^2=5^2=3^2=16, SO=4

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

🎥 Видео

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Найти площадь квадрата описанного около окружности радиуса 19Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать

Вычисление радиуса сферы, описанной около правильной треугольной пирамидыСкачать

Найти центр и радиус окружностиСкачать

Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать