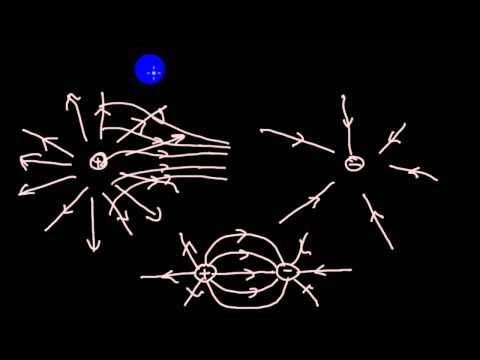
В предыдущей статье было показано, что вследствие поляризации диэлектрика, т. е. смещения его связанных зарядов, изменяется напряженность электрического поля. Результирующее влияние диэлектрика на электрическое поле оценивают векторной величиной, называемой поляризованностью Р (вектором поляризации).
Средняя интенсивность поляризации Pср определяется как сумма дипольных моментов в единице объема диэлектрика, а чтобы найти поляризованность в данном месте поля, надо выбрать достаточно малый объем ΔV:
Единица измерения поляризованности
[P] = [ql/V] = Кл*м/м 3 = Кл/м 2.
Вектор поляризации направлен навстречу вектору напряженности электрического поля связанных зарядов Eп.(рис. 4.12).
Вектор поляризации для большинства диэлектриков (за исключением группы сегнетоэлектриков) пропорционален напряженности электрического поля:
и его направление совпадает с направлением внешнего Eвн и результирующего Е полей (риc. 4.12).
Коэффициент k называется электрической восприимчивостью диэлектрика и характеризует его способность поляризоваться.
При расчетах электрических полей в диэлектриках с различными диэлектрическими проницаемостями пользуются еще вектором электрического смещения.
Электрическое смещение D связано с напряженностью электрического ноля простым соотношением
откуда можно определить единицу намерения электрического смещения:
которая такая же, как у вектора, поляризации и у поверхностной плотности зарядов на электродах.
Электрическое смещение и поверхностная плотность свободных зарядов численно одинаковы на поверхности всех проводящих тел, находящихся в электростатическом поле. Например, у внутренней поверхности пластины плоского конденсатора (рис. 4.8) напряженность однородного электрического поля, как и в любой точке однородного поля (4.10),
а электрическое смещение в любой точке поля, в том числе и у металлической поверхности,
т. е. совпадает с поверхностной плотностью заряда на пластине.
Из (2а) следует, что при заданной плотности поверхностных свободных зарядов на электродах электрическое смещение в однородном диэлектрике с диэлектрической проницаемостью εa не зависит от εa, а напряженность электрического поля зависит. Поэтому можно сказать, что на напряженность электрического поля определяется и свободными (на электродах) и связанными (в диэлектриках) зарядами, т. е. поляризацией диэлектрика, а электрическое смещение в однородном диэлектрике не зависит от связанных зарядов.
Связь между тремя векторными величинами, характеризующими электрическое поле в диэлектрике, выражается равенством
Приняв во внимание (1) и (2), получим
откуда диэлектрическая проницаемость
а электрическая восприимчивость

Рассмотрим еще неоднородное электрическое поле заряженного металлическою шара (рис. 1), радиус которого Rш. Известно, что электрический заряд Q находится на поверхности такого шара. Поверхностная плотность заряда
Поле металлического шара с зарядом Q совпадает вне шара с полем равного ему по значению точечного заряда Q, расположенного в центре шара (4.8); поэтому напряженность поля на расстоянии R от центра шара и в частности, у его наружной поверхности, т.е. при R = Rш,
а электрическое смещение
т. е. равно поверхностной плотности заряда.
Внутри металлического шара поля нет, как и во всяком проводнике в условиях электростатики , Поэтому потенциалы всех точек шара одинаковые, т. е. шар — эквипотенциальное тело, как и всякое металлическое тело в электростатическом поле.
Аналогично потоку вектора напряженности поля (4.7) применяется понятие потока вектора электрического смешения.
Поток вектора смещения ND в однородном поле равен произведению численного значения вектора смещения D и площадки S, во всех точках которой вектор смещения имеет одинаковое значение и направлен перпендикулярно к ней, т. е.
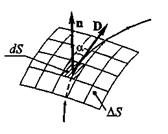
При неоднородном поле произвольную поверхность площадью S разбивают на элементарные, в пределах каждой на которых смещение одинаково; так что поток вектора
смещения через такую элементарную площадку
где Dn— нормальная составляющая вектора смещения (перпендикулярная к элементарной площадке).
Поток вектора смещения через произвольную замкнутую поверхность находится суммированием элементарных потоков: 
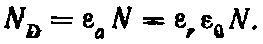
В частности, в случае шаровой поверхности
Таким образом, поток вектора электрического смещения через шаровую поверхность равен заряду, расположенному внутри поверхности.
Полученное выражение ND = Q справедливо для замкнутой поверхности любой формы, охватывающей заряд как в однородной среде с εr = const, так и в среде, диэлектрическая проницаемость которой неодинакова в различных участках среды, например в двухслойном конденсаторе.
На поверхности шара,
откуда определяется электрическое смещение у поверхности шара: что согласуется с (5).
Видео:45. Электрическое смещениеСкачать

Вопрос №1. Электрическое смещение. Поток смещения.
Лекция № 4
Расчет полей заданных электрических зарядов
План лекции:
1. Электрическое смещение. Поток смещения.
2. Теорема Гаусса для электрического поля в диэлектрике.
3. Расчет поля равномерно заряженных бесконечных плоскостей.
4. Напряженность и потенциал поля равномерно заряженной сферической поверхности.
5. Напряженность и потенциал поля объемно заряженного шара.
6. Напряженность и потенциал заряженных цилиндра, бесконечной прямой нити.
Вопрос №1. Электрическое смещение. Поток смещения.
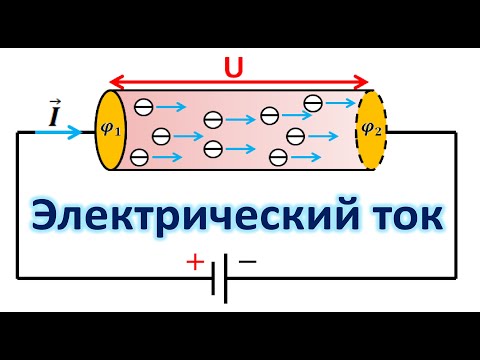
Для описания электростатического поля используют его силовую характеристику — напряженность поля Е. Эта величина зависит от свойств среды, которые определяются диэлектрической проницаемостью е в выражении:
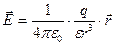
В диэлектрической среде напряженность поля определяется как свободными, так и связанными зарядами.
Связанными зарядами называются заряды, которые входят в состав атомов и молекул, а также заряды ионов в кристаллических диэлектриках с ионной решеткой. Свободные заряды— это заряды частиц, способных перемещаться под действием электрического поля на макроскопические расстояния (электроны проводимости в металлах и полупроводниках, электроны в вакууме, ионы в электролитах и ионизированных газах). К свободным относятся также избыточные заряды, сообщаемые телу и нарушающие его электростатическую нейтральность (например, заряды, нанесенные извне на поверхность диэлектрика).
Чтобы при описании поля в изотропной среде (диэлектрике) скомпенсировать влияние этой среды на напряженность Е (Е = Ео / ε), вводят дополнительную характеристику поля, называемую электрическим смещением 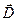
|
В случае точечного заряда проекция вектора 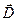
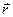
|
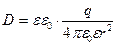
Из выражения (1.2) видно, что электрическое смещение 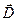
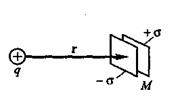
Электрическое смещение в определенной небольшой области пространства можно измерить с помощью «пластинок Ми», которые представляют собой обкладки плоского конденсатора. Если расположить эти пластинки на некотором расстоянии rот точечного заряда qи сориентировать так, чтобы их плоскость была перпендикулярна вектору Из выражения (1.2) видно, что электрическое смещение фактически характеризует интенсивность поля, создаваемого только свободными зарядами. Так же как и напряженность Е, электрическое смещение D удовлетворяет принципу суперпозиции. Аналогично вводят линии электрического смещения, направление и густота которых удовлетворяют тем же правилам, которые справедливы для линий напряженности. Для расчета электростатических полей большое значение имеет поток электрического смещения Ф, который вводится следующим образом.
|

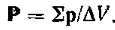

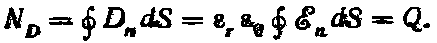
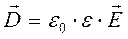
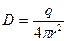
 . Тогда элементарным потоком вектора смещения
. Тогда элементарным потоком вектора смещения 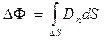
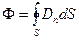 — определение потока вектора D.
— определение потока вектора D.



 то
то




 — и
— и 

 (тангенциальная составляющая
(тангенциальная составляющая