Найти точки пересечения окружности ( x — 1) 2 + (y — 2) 2 = 4 и прямой y = 2x.
Координаты точек пересечения должны удовлетворять обоим указанным уравнениям, так как эти точки находятся как на одной, так и на другой линии. Решим систему уравнений
Подставляя в первое уравнение 2x вместо y и раскрывая скобки, получим
Подставляя эти значения во второе уравнение y = 2x, получим
и
.
- Пересечение окружности и прямой
- Решение
- Реализация
- Виды пересечения окружности прямой
- Пересечение окружности и прямой
- Решение
- Реализация
- Пересечение окружности и прямой.Координаты.
- Отрезки и прямые, связанные с окружностью. Теорема о бабочке
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- 📺 Видео
Видео:Определение точки пересечения окружности с прямойСкачать

Пересечение окружности и прямой
Дана окружность (координатами своего центра и радиусом) и прямая (своим уравнением). Требуется найти точки их пересечения (одна, две, либо ни одной).
Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать

Решение
Вместо формального решения системы двух уравнений подойдём к задаче с геометрической стороны (причём, за счёт этого мы получим более точное решение с точки зрения численной устойчивости).
Предположим, не теряя общности, что центр окружности находится в начале координат (если это не так, то перенесём его туда, исправив соответствующе константу C в уравнении прямой). Т.е. имеем окружность с центром в (0,0) радиуса r и прямую с уравнением Ax + By + C = 0.
Сначала найдём ближайшую к центру точку прямой — точку с некоторыми координатами (x0,y0). Во-первых, эта точка должна находиться на таком расстоянии от начала координат:
Во-вторых, поскольку вектор (A,B) перпендикулярен прямой, то координаты этой точки должны быть пропорциональны координатам этого вектора. Учитывая, что расстояние от начала координат до искомой точки нам известно, нам нужно просто нормировать вектор (A,B) к этой длине, и мы получаем:
(здесь неочевидны только знаки ‘минус’, но эти формулы легко проверить подстановкой в уравнение прямой — должен получиться ноль)
Зная ближайшую к центру окружности точку, мы уже можем определить, сколько точек будет содержать ответ, и даже дать ответ, если этих точек 0 или 1.
Действительно, если расстояние от (x0, y0) до начала координат (а его мы уже выразили формулой — см. выше) больше радиуса, то ответ — ноль точек. Если это расстояние равно радиусу, то ответом будет одна точка — (x0,y0). А вот в оставшемся случае точек будет две, и их координаты нам предстоит найти.
Итак, мы знаем, что точка (x0, y0) лежит внутри круга. Искомые точки (ax,ay) и (bx,by), помимо того что должны принадлежать прямой, должны лежать на одном и том же расстоянии d от точки (x0, y0), причём это расстояние легко найти:
Заметим, что вектор (-B,A) коллинеарен прямой, а потому искомые точки (ax,ay) и (bx,by) можно получить, прибавив к точке (x0,y0) вектор (-B,A), нормированный к длине d (мы получим одну искомую точку), и вычтя этот же вектор (получим вторую искомую точку).
Окончательное решение такое:
Если бы мы решали эту задачу чисто алгебраически, то скорее всего получили бы решение в другом виде, которое даёт бОльшую погрешность. Поэтому «геометрический» метод, описанный здесь, помимо наглядности, ещё и более точен.
Видео:Взаимное расположение и точки пересечения прямой и окружностиСкачать

Реализация
Как и было указано в начале описания, предполагается, что окружность расположена в начале координат.
Поэтому входные параметры — это радиус окружности и коэффициенты A,B,C уравнения прямой.
Видео:Пересечение прямой и окружностиСкачать

Виды пересечения окружности прямой
Видео:Алгоритмы. Пересечение окружностейСкачать

Пересечение окружности и прямой
Дана окружность (координатами своего центра и радиусом) и прямая (своим уравнением). Требуется найти точки их пересечения (одна, две, либо ни одной).
Видео:Нахождение точки, лежащей на окружностиСкачать
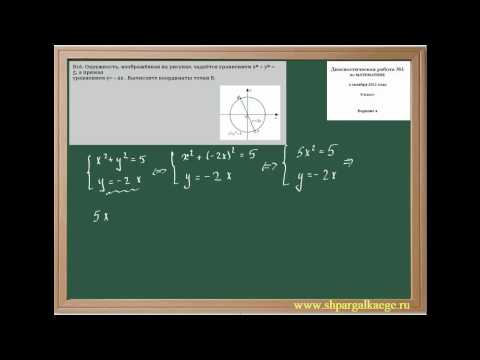
Решение
Вместо формального решения системы двух уравнений подойдём к задаче с геометрической стороны (причём, за счёт этого мы получим более точное решение с точки зрения численной устойчивости).
Предположим, не теряя общности, что центр окружности находится в начале координат (если это не так, то перенесём его туда, исправив соответствующе константу C в уравнении прямой). Т.е. имеем окружность с центром в (0,0) радиуса r и прямую с уравнением Ax + By + C = 0.
Сначала найдём ближайшую к центру точку прямой — точку с некоторыми координатами (x0,y0). Во-первых, эта точка должна находиться на таком расстоянии от начала координат:
Во-вторых, поскольку вектор (A,B) перпендикулярен прямой, то координаты этой точки должны быть пропорциональны координатам этого вектора. Учитывая, что расстояние от начала координат до искомой точки нам известно, нам нужно просто нормировать вектор (A,B) к этой длине, и мы получаем:
(здесь неочевидны только знаки ‘минус’, но эти формулы легко проверить подстановкой в уравнение прямой — должен получиться ноль)
Зная ближайшую к центру окружности точку, мы уже можем определить, сколько точек будет содержать ответ, и даже дать ответ, если этих точек 0 или 1.
Действительно, если расстояние от (x0, y0) до начала координат (а его мы уже выразили формулой — см. выше) больше радиуса, то ответ — ноль точек. Если это расстояние равно радиусу, то ответом будет одна точка — (x0,y0). А вот в оставшемся случае точек будет две, и их координаты нам предстоит найти.
Итак, мы знаем, что точка (x0, y0) лежит внутри круга. Искомые точки (ax,ay) и (bx,by), помимо того что должны принадлежать прямой, должны лежать на одном и том же расстоянии d от точки (x0, y0), причём это расстояние легко найти:
Заметим, что вектор (-B,A) коллинеарен прямой, а потому искомые точки (ax,ay) и (bx,by) можно получить, прибавив к точке (x0,y0) вектор (-B,A), нормированный к длине d (мы получим одну искомую точку), и вычтя этот же вектор (получим вторую искомую точку).
Окончательное решение такое:
Если бы мы решали эту задачу чисто алгебраически, то скорее всего получили бы решение в другом виде, которое даёт бОльшую погрешность. Поэтому «геометрический» метод, описанный здесь, помимо наглядности, ещё и более точен.
Видео:Пересечения прямых, лучей, отрезковСкачать

Реализация
Как и было указано в начале описания, предполагается, что окружность расположена в начале координат.
Поэтому входные параметры — это радиус окружности и коэффициенты A,B,C уравнения прямой.
Видео:Пересечение прямой и плоскостиСкачать

Пересечение окружности и прямой.Координаты.
| Элементы окружности или координаты |
| x^2+y^2+ x+ y+ =0 |
| Элементы прямой линии |
| Уравнение окружности |
| Уравнение прямой к угловым коэффициентом |
| Координаты пересечения окружности и прямой |
Рассмотрим более подробно задачу пересечения окружности и прямой. В принципе само решение есть уже в общем виде Пересечение прямой и кривой второго порядка, но мы рассмотрим и выведем формулы точек пересечения этих двух геометрических объектов.
Уравнение прямой, как мы знаем из материала Расчет параметров прямой линии по заданным параметрам могут быть заданы в нескольких видах:
— с угловым коэффициентом
— в нормальном виде
Что бы решить нашу первоначальную задачу, использовать будем уравнение прямой с угловым коэффициентом которое имеет вид
Уравнение окружности тоже может быть выражена в различных видах
Например в общем виде оно имеет вид
Подставим в уравнение окружности, уравнение прямой
Мы получили стандартное квадратное уравнение, решив котрое мы получим два значения, которые и будут являтся абсциссами точек пересечения прямой и окружности.
Подставим эти координаты в уравнение прямой, мы получим две ординаты точек пересечения.
Таким образом решение найдено.
Для упрощения, для сверки результатов — калькулятор помогает Вам рассчитать эти точки. Интересная особенность состоит в том, что прямая может быть задана в любом виде, хоть виде двух точек.
А уравнение окружности может быть не только введено с помощью коэффицентов, но и в виде пары трех координат через которые, эта окружность будет проходить.
Видео:Точка встречи прямой с плоскостьюСкачать

Отрезки и прямые, связанные с окружностью. Теорема о бабочке
 Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства |
| Окружность |  |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
Видео:Найти точку пересечения прямой и плоскостиСкачать

Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.
Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема |
| Пересекающиеся хорды |  |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.


| Пересекающиеся хорды | ||
 | ||
| Касательные, проведённые к окружности из одной точки | ||
 | ||
| Касательная и секущая, проведённые к окружности из одной точки | ||
 | ||
| Секущие, проведённые из одной точки вне круга | ||
 | ||
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Видео:Пересечение прямой и плоскостиСкачать

Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
📺 Видео
Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Уравнение окружности (1)Скачать

Нахождение точки пересечения прямой и треугольникаСкачать

Пересечение прямой линии с плоскостью Определение видимости прямойСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Теорема о числе точек пересечения окружности и прямойСкачать
































