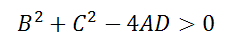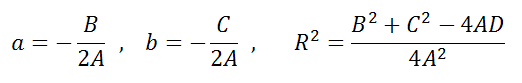Разделы: Математика
- углубить знания по темам «окружность» и «дополнительные построения», расширение математических познаний;
- совершенствовать навыки доказательств теорем;
- изучить метод решения геометрических задач с помощью свойств радикальной оси двух окружностей.
- развивать учебно-познавательную деятельность обучающихся;
- развивать логическое мышление и умения применять знания в нестандартных ситуациях.
3. Воспитательная: воспитывать аккуратность, культуру математической речи.
Оборудование: мел, доска, проектор.
Тип урока: изучение нового и первичное закрепления новых знаний.
- Организационный момент – 2 мин.
- Вступительное слово учителя – 1 мин.
- Актуализация опорных знаний – 1 мин.
- Формирование нового – 30 мин.
- Первичное закрепление – 10 мин.
- Рефлексия – 1 мин.
1. Организационный момент. Приветствие.
2. Вступительное слово.
Если отслеживать историю достижений учащихся на математических соревнованиях, то можно не раз заметить такую картину: до 9 класса ученик очень успешно выступает на различных олимпиадах, однако почему то в 10 классе его результаты сильно понижаются. Трудно полностью объяснить причину подобного, однако, несомненно, что это отчасти связано с существенным различием в уровне задач 9 и 10 классов. Непосвященному это трудно заметить. Например, остановимся геометрических задачах, связанных с окружностью. В большинстве случаев такие задачи можно решить методами 9 классов, однако, такое решение будет слишком громоздким и отнимет много времени на оформление, что в виду ограниченности времени на олимпиадах далеко не всегда осуществимо. Поэтому изучение методов 10 класса для решения задач является жизненной необходимостью для успешного участия на олимпиадах, хотя в истории бывали и исключения, когда некоторые умудрялись решить сложную задачу 10 класса методами 9 класса.
3. Актуализация опорных знаний.
Традиционно на олимпиадах есть хотя бы одна геометрическая задача, а среди таких задач наибольшую трудность вызывают задачи связанные с окружностями. Несмотря на то, что не существует общего метода решения всех геометрических задач, связанных с окружностью, для решения достаточно большого класса таких задач оказываются полезным свойства радикальной оси, поляр, полюсов и некоторых элементов проективной геометрии. Сегодня мы начнем изучение некоторых первичных свойств радикальной оси, однако даже эти свойства могут быть полезны для решения сложных геометрических задач, которые встречаются на международных олимпиадах. Также мы разберем решения нескольких задач российских геометрических олимпиад, заслуженно признанных одними из самых сложных по геометрии.
4. Формирование нового.
Определение 1 (см. [1], стр. 122). Пусть дана окружность ω с центром в точке О и радиусом R. Степенью точки М относительно окружности ω называется число ОМ 2 – R 2 .
Определение 2 (см. [1], стр. 122). Пусть даны две окружности ω1 и ω2. Радикальной осью двух окружностей называется множество всех точек плоскости, каждая из которых имеет равные степени относительно этих окружностей.
Теорема 1. Пусть даны две окружности ω1 и ω2, центры которых различны. Тогда для этих окружностей радикальная ось существует и является прямой линией.
- Если две окружности ω1 и ω2 пересекаются в двух различных точках, то радикальная осью этих окружностей является прямая проходящая через точки их пересечения.
- Если две окружности ω1 и ω2 касаются внешним или внутренним образом, то их радикальная ось совпадает с общей касательной в точке касания окружностей.
- Если две окружности ω1 и ω2 лежат одна вне другой, не касаясь, то радикальная ось содержит середины общих касательных этих окружностей.
Доказательство. Вне зависимости от того как пересекаются окружности согласно теореме о том, что разность квадратов наклонных, проведенных из одной точки, равна разности квадратов из проекций на прямую, геометрическим местом точек, имеющих одинаковые степени относительно двух заданных окружностей, является прямая, перпендикулярная линии центров окружностей. Для того, чтобы однозначно знать положение прямой достаточно знать две ее точки.
 |  |  |
| I | I I | I I I |
В первом случае, когда окружности пересекаются в двух точках, эти точки будут иметь равные степени относительно них, равные нулю, поэтому радикальной осью для таких окружностей будет прямая, проходящая через точки пересечения окружностей.
Во втором случае, когда окружность каются внешним или внутренним образом, также общая точка окружностей будет иметь одинаковые степени относительно них, значит, в этом случае радикальной осью будет прямая, проходящая через точку касания окружностей и перпендикулярная их линии центром.
В третьем случае, радикальная ось будет проходить через середины отрезков общих касательных, поскольку степенью точки этих точки является квадрат отрезка касательной, проведенной из точки к окружности.
Замечание 1. Теорема 1 применима и в случае, если радиус одной из окружностей равен нулю.
Пример 1 (см. [2], стр. 64, задача №3.65). На окружности S с диаметром AB взята точка C, из точки C опущен перпендикуляр CH на прямую AB. Докажите, что общая хорда окружности S и окружности S1 с центром C и радиусом CH делит отрезок CH пополам.
Решение (см. [2], стр. 76). Пусть M – середина отрезка CH. Докажем, что точка M лежит на радикальной оси окружностей S и S1, т.е. её степени относительно этих окружностей равны. Пусть радиусы окружностей S и S1 равны 2R и 2r.
Тогда степень точки M относительно окружности S1 равна CM 2 – 4r 2 = -3r 2 , а её степень относительно S равна OM 2 – 4R 2 , где O – середина отрезка AB. Ясно, что OH 2 = 4R 2 – 4r 2 , поэтому OM 2 = 4R 2 – 4r 2 + r 2 = 4R 2 – 3r 2 . Следовательно, OM 2 – 4R 2 = -3r 2 . Таким образом, точка М лежит на ED, следовательно, ED делит CH пополам.
Теорема 2 (см. [1], стр.125). Если центры трех окружностей неколлинеарные, то три радикальные оси этих окружностей, взятых попарно, имеют общую точку.
Доказательство. Пусть даны три окружности Ω1, Ω2, Ω3, центры которых неколлинеарные.
Поскольку центры трех окружностей неколлинеарные, то прямые перпендикулярные O1O2 и O1O3 пересекаются, значит, не параллельны и радикальные оси к Ω1 и Ω2, а также к Ω1 и Ω3 пересекаются в некоторой точке, которую обозначим буквой Е. Отсюда, степени точки Е относительно Ω1 и Ω2 равны, и относительно Ω1 и Ω3 тоже равны. Следовательно, точки Е имеет одинаковые степени относительно Ω2 и Ω3, а это означает, что она лежит на радикальной оси к окружностям Ω2 и Ω3, т.е. все три радикальные оси пересекаются в одной точке. Что и требовалось доказать.
Пример 2 (Турнир городов, весенний тур, базовый вариант, 10-11 класс, 2012 г.). Четырехугольник ABCD без параллельных сторон вписан в окружность. Для каждой пары касающихся окружностей, одна из которых имеет хорду AB, а другая – хорду CD, отметим их точку касания X. Докажите, что все такие точки X лежат на одной окружности.
Решение (см. [3]). обозначим через Ω1 и Ω2 касающиеся окружности, содержащие соответственно хорды AB и СD, а через Ω – описанную окружность четырехугольника ABCD. Пусть O – точка пересечения прямых AB и СD.
Тогда согласно теореме 1 прямая AB – радикальная ось окружностей Ω1 и Ω, CD – радикальная ось окружностей Ω2 и Ω, а общая касательная окружностей Ω1 и Ω2 – их радикальная ось. Согласно теореме 2 эти три радикальные оси пересекаются в одной точке, которую обозначим буквой O.
При этом квадрат длина касательной OX равна степени точки O относительно Ω1, то есть OA× OB, значит, что точка X лежит на окружности с центром О и радиусом 
Пример 3 (Московская устная олимпиада по геометрии, 8-9 класс, 2005). Дан шестиугольник ABCDEF, в котором AB = BC, CD = DE, EF = FA, а углы A и C – прямые. Докажите, что прямые FD и BE перпендикулярны.
Решение №1 (см. [3]). Поскольку по теореме Пифагора
BD 2 + EF 2 = BC 2 + CD 2 + EF 2 = AB 2 + DE 2 + AF 2 = BF 2 + DE 2 , то согласно критерию перпендикулярности диагоналей выпуклого четырехугольника FD и BE перпендикулярны.
 |  |
Решение №2 (см. [3]). Рассмотрим окружности с центрами D и F и радиусами DC и EF соответственно. Тогда BA = BC – касательные к этим окружностям, а точка E принадлежит обеим окружностям, поэтому BE – их радикальная ось, и следовательно, она перпендикулярна линии центров FD.
5. Первичное закрепление.
(Всероссийская олимпиада по математике, 10 класс, 2011 г.) Периметр треугольника ABC равен 4. На лучах AB и AC отмечены точки X и Y так, что AX = AY = 1. Отрезки BC и XY пересекаются в точке M. Докажите, что периметр одного из треугольников ABM и ACM равен 2.
(Московская устная олимпиада по геометрии, 10-11 класс, 2011 г.) Дана неравнобокая трапеция ABCD (AB ǁ CD). Произвольная окружность, проходящая через точки A и B, пересекает боковые стороны трапеции в точках P и Q, а диагонали – в точках M и N. Докажите, что прямые PQ, MN и CD пересекаются в одной точке.
(Всероссийская олимпиада по математике, 11 класс, 2005 г.) Пусть AA1 и BB1 – высоты остроугольного неравнобедренного треугольника ABC. Известно, что отрезок A1B1 пересекает среднюю линию, параллельную AB, в точке C’. Докажите, что отрезок CC’ перпендикулярен прямой, проходящей через точку пересечения высот и центр описанной окружности треугольника ABC.
— Что особенно сегодня вам запомнилось?
— Полезно ли для решения некоторых геометрических задач знать свойства радикальной оси двух окружностей?
- Декартовы координаты точек плоскости. Уравнение окружности
- Числовая ось
- Прямоугольная декартова система координат на плоскости
- Формула для расстояния между двумя точками координатной плоскости
- Уравнение окружности на координатной плоскости
- Окружность на координатной плоскости
- Окружность радиуса R с центром в начале координат представляется уравнением:
- Как найти радиус и центр окружности
- 📽️ Видео
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Декартовы координаты точек плоскости. Уравнение окружности
 Числовая ось Числовая ось |
 Прямоугольная декартова система координат на плоскости Прямоугольная декартова система координат на плоскости |
 Формула для расстояния между двумя точками координатной плоскости Формула для расстояния между двумя точками координатной плоскости |
 Уравнение окружности на координатной плоскости Уравнение окружности на координатной плоскости |
Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Числовая ось
Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление
указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.
Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .
Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .
Видео:Тригонометрическая окружность. Как выучить?Скачать

Прямоугольная декартова система координат на плоскости
Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).
Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.
Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA1 и AA2 на прямые Ox и Oy соответственно (рис.3).
Определение 4 . Абсциссой точки A называют координату точки A1 на числовой оси Ox , ординатой точки A называют координату точки A2 на числовой оси Oy .
Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).
Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .
Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).
Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.
Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .
Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Формула для расстояния между двумя точками координатной плоскости
Утверждение 1 . Расстояние между двумя точками координатной плоскости
вычисляется по формуле
Доказательство . Рассмотрим рисунок 6.
| | A1A2| 2 = = ( x2 – x1) 2 + ( y2 – y1) 2 . | (1) |
что и требовалось доказать.
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Уравнение окружности на координатной плоскости
Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:
Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A0 (x0 ; y0) .
Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид
Видео:Оси симметрии прямоугольника, равнобедренного треугольника, окружностиСкачать

Окружность на координатной плоскости
Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.
Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Окружность радиуса R с центром в начале координат представляется уравнением:
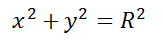
Окружность радиуса R с центром в точке C(a;b) представляется уравнением:
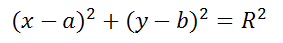
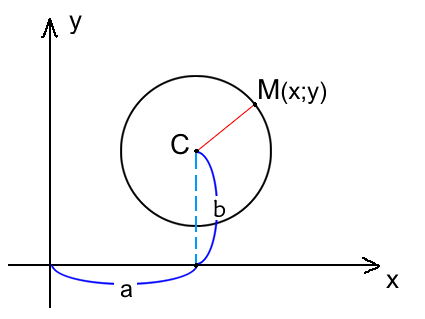
Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия ).
Это уравнение можно записать в виде: 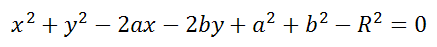
Если уравнение помножить на любое число A, то получим
Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.
Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x 2 и y 2 были равны в уравнение вида: 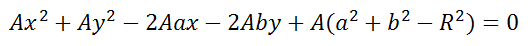
3. Если выполняется неравенство
Видео:Ось симметрииСкачать

Как найти радиус и центр окружности
Уравнение Ax 2 +Bx+Ay 2 +Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:
Пример 1
Уравнение 5x 2 -10x+5y 2 +20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство
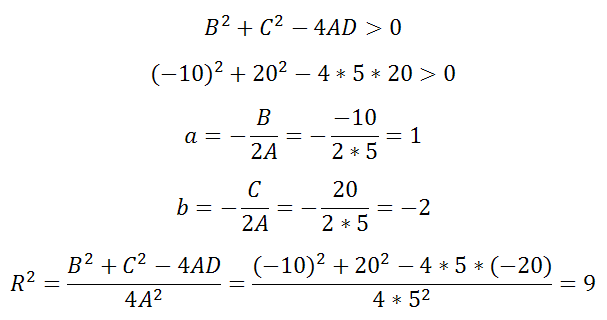
Решая, получаем что центр есть (1;-2), а радиус R=3
Анимационный график окружности
Пример 2
Уравнение второй степени x 2 +4xy+y 2 =1 не является окружностью, так как в нём есть член 4xy.
Пример 3
Уравнение второй степени 4x 2 +9y 2 =36 не представляет окружность, так как в нём коэффициенты при x 2 и y 2 не равны.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.3 / 5. Количество оценок: 4
📽️ Видео
Физика - движение по окружностиСкачать

Уравнение окружности (1)Скачать

Как найти координаты точек на тригонометрической окружностиСкачать

Марафон на тему: «Тригонометрия: задания 6 и 13»Скачать

ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать

Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

8 класс, 9 урок, Осевая и центральная симметрияСкачать

Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

Уравнение окружности с центром на оси абсцисс, ординат или в начале координат. Урок 3. Геометрия 8.Скачать

Деление окружности на 3; 6; 12 равных частейСкачать

Центральная симметрия. 6 класс.Скачать

Как найти центр круга или разделить трубу на две равных части.Скачать