Как найти объем правильного треугольника

В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.

Видео:Как найти площадь треугольника без формулы?Скачать

Формула вычисления объема пирамиды

1. Общая формула

Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.

• ABCD – основание;
• E – вершина;
• h – высота, перпендикулярная основанию.

2. Объем правильной треугольной пирамиды

Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):

Подставляем данное выражение в формулу расчета объема фигуры и получаем:

3. Объем правильной четырехугольной пирамиды

Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a 2 , где а – длина его стороны.

Следовательно, формулу объема можно представить в виде:

4. Объем правильной шестиугольной пирамиды

Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):

С учетом этого, объем фигуры считается так:

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Примеры задач

Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:

Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.

Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см 2 (3 см ⋅ 3 см). Следовательно, объем равен:

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Объем треугольной пирамиды. Формулы и пример решения задачи

Главной характеристикой любой геометрической фигуры в пространстве является ее объем. В данной статье рассмотрим, что собой представляет пирамида с треугольником в основании, а также покажем, как находить объем треугольной пирамиды — правильной полной и усеченной.

Видео:🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Что это — треугольная пирамида?

Каждый слышал о древних египетских пирамидах, тем не менее они являются четырехугольными правильными, а не треугольными. Объясним, как получить треугольную пирамиду.

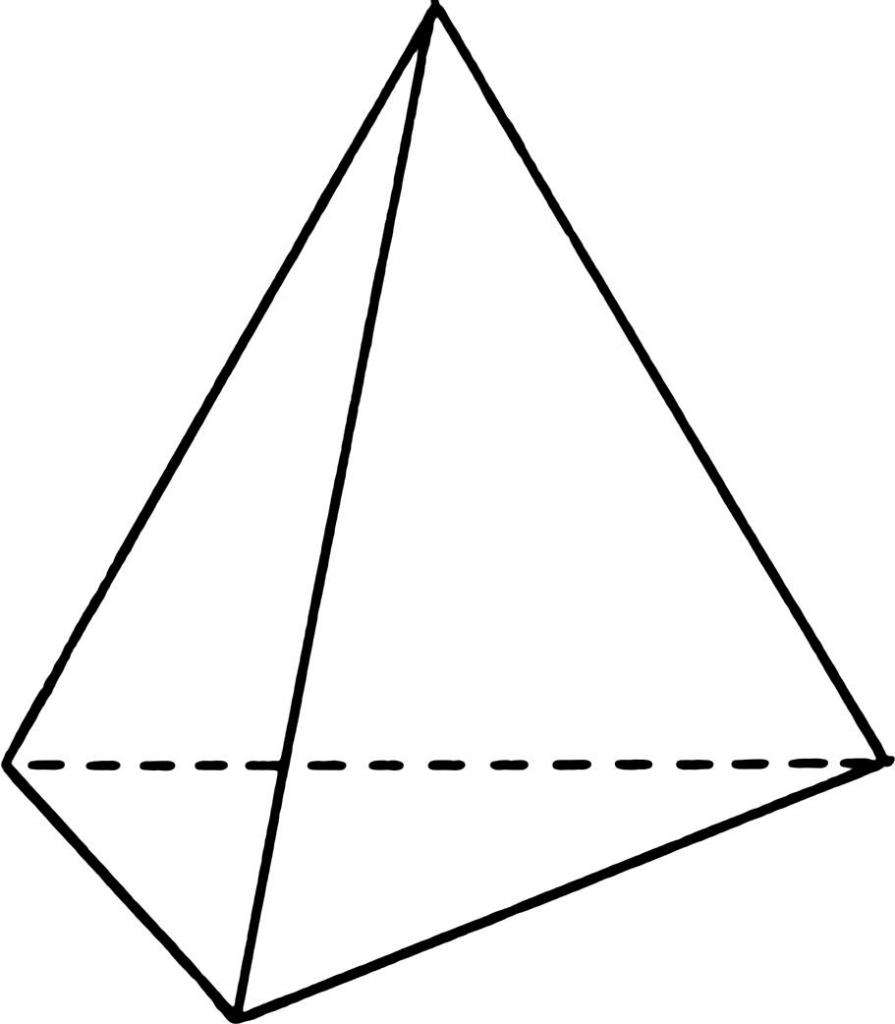
Возьмем произвольный треугольник и соединим все его вершины с некоторой одной точкой, расположенной вне плоскости этого треугольника. Образованная фигура будет называться треугольной пирамидой. Она показана на рисунке ниже.

Вам будет интересно: Кашмирский конфликт: участники, причины, ход событий

Как видно, рассматриваемая фигура образована четырьмя треугольниками, которые в общем случае являются разными. Каждый треугольник — это стороны пирамиды или ее грань. Эту пирамиду часто называют тетраэдром, то есть четырехгранной объемной фигурой.

Помимо сторон, пирамида также обладает ребрами (их у нее 6) и вершинами (их 4).

Видео:Формула объёма прямоугольного параллелепипеда (для 3В)Скачать

Правильная пирамида с треугольным основанием

Фигура, которая получена с использованием произвольного треугольника и точки в пространстве, будет неправильной наклонной пирамидой в общем случае. Теперь представим, что исходный треугольник имеет одинаковые стороны, а точка пространства расположена точно над его геометрическим центром на расстоянии h от плоскости треугольника. Построенная с использованием этих исходных данных пирамида будет правильной.

Очевидно, что число ребер, сторон и вершин у правильной треугольной пирамиды будет таким же, как у пирамиды, построенной из произвольного треугольника.

Однако правильная фигура обладает некоторыми отличительными чертами:

• ее высота, проведенная из вершины, точно пересечет основание в геометрическом центре (точка пересечения медиан);
• боковая поверхность такой пирамиды образована тремя одинаковыми треугольниками, которые являются равнобедренными или равносторонними.

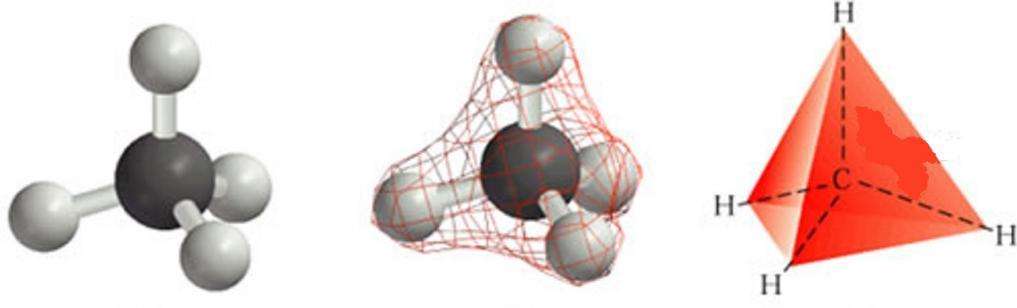
Правильная треугольная пирамида является не только чисто теоретическим геометрическим объектом. Некоторые структуры в природе имеют ее форму, например кристаллическая решетка алмаза, где атом углерода соединен с четырьмя такими же атомами ковалентными связями, или молекула метана, где вершины пирамиды образованы атомами водорода.

Видео:Найдите объем треугольной призмыСкачать

Формулы объема треугольной пирамиды

Определить объем совершенно любой пирамиды с произвольным n-угольником в основании можно с помощью следующего выражения:

Здесь символ So обозначает площадь основания, h — это высота фигуры, проведенная к отмеченному основанию из вершины пирамиды.

Поскольку площадь произвольного треугольника равна половине произведения длины его стороны a на апофему ha, опущенную на эту сторону, то формула объема треугольной пирамиды может быть записана в следующем виде:

V = 1/6 × a × ha × h

Для треугольной пирамиды общего типа определение высоты является непростой задачей. Для ее решения проще всего воспользоваться формулой расстояния между точкой (вершиной) и плоскостью (треугольным основанием), представленной уравнением общего вида.

Для правильной пирамиды формула объема имеет конкретный вид. Площадь основания (равностороннего треугольника) для нее равна:

Подставляем ее в общее выражение для V, получаем:

Частным случаем является ситуация, когда у тетраэдра все стороны оказываются одинаковыми равносторонними треугольниками. В этом случае определить его объем можно, только исходя из знания параметра его ребра a. Соответствующее выражение имеет вид:

Видео:Математика | Объём в жизни и в математикеСкачать

Усеченная пирамида

Если верхнюю часть, содержащую вершину, отсечь у правильной треугольной пирамиды, то получится усеченная фигура. В отличие от исходной она будет состоять из двух равносторонних треугольных оснований и трех равнобедренных трапеций.

Ниже на фото показано, как выглядит правильная усеченная пирамида треугольная, изготовленная из бумаги.

Для определения объема треугольной пирамиды усеченной необходимо знать три ее линейных характеристики: каждую из сторон оснований и высоту фигуры, равную расстоянию между верхним и нижним основаниями. Соответствующая формула для объема записывается так:

V = √3/12 × h × (A2 + a2 + A × a)

Здесь h — высота фигуры, A и a — длины сторон большого (нижнего) и малого (верхнего) равносторонних треугольников соответственно.

Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Решение задачи

Чтобы приведенная информация в статье была понятнее для читателя, покажем на наглядном примере, как пользоваться некоторыми из записанных формул.

Пусть объем треугольной пирамиды равен 15 см3. Известно, что фигура является правильной. Следует найти апофему ab бокового ребра, если известно, что высота пирамиды составляет 4 см.

Поскольку известны объем и высота фигуры, то можно воспользоваться соответствующей формулой для вычисления длины стороны ее основания. Имеем:

a = 12 × V / (√3 × h) = 12 × 15 / (√3 × 4) = 25,98 см

Апофему ab можно рассчитать, если рассмотреть соответствующий прямоугольный треугольник внутри пирамиды. Катетами треугольника являются 1/3 длины высоты основания и высота пирамиды, гипотенузой будет искомая апофема. Тогда:

ab = √(h2 + a2 / 12) = √(16 + 25,982 / 12) = 8,5 см

Рассчитанная длина апофемы фигуры получилась больше ее высоты, что справедливо для пирамиды любого типа.

Видео:Математика 5 Объем Объем прямоугольного параллелепипедаСкачать

Объем треугольной пирамиды

Многогранник, в основании которого лежит правильный треугольник, а остальные грани представлены равнобедренными треугольниками называется треугольной пирамидой. Еще такую пирамиду называют тетраэдром.

Правильная пирамида обладает множеством свойств, которые выводятся из составляющих ее фигур:

• Все стороны основания равны между собой, потому что оно представлено правильным треугольником;
• Все ребра пирамиды также равны между собой;
• Т.к. каждая грань образует равнобедренный треугольник, в котором ребра равны и основания равны, то можно сказать, что площадь каждой грани одинакова;
• Все двугранные углы при основании равны.

Площадь треугольной пирамиды рассчитывается, как сумма площадей основания и боковой развертки. Также ее можно найти, если рассчитать площадь одной из боковых граней и основания. Формула объема треугольной пирамиды также выводится из свойств треугольников, из которых она состоит:

Площадь основания рассчитывается из формулы площади правильного треугольника:

Рассмотрим пример расчета объема треугольной пирамиды.

Используя эту формулу, важно строго следить за подсчетами и сокращениями. Одна маленькая ошибка может привести к неверному результату. В целом, найти объем правильной треугольной пирамиды очень просто.

🎬 Видео

КАК НАЙТИ ОБЪЕМ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА? Примеры | МАТЕМАТИКА 5 классСкачать

Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

5 класс, 21 урок, Объемы. Объем прямоугольного параллелепипедаСкачать

Нахождение стороны прямоугольного треугольникаСкачать

НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

КАК НАЙТИ ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

8 класс, 14 урок, Площадь треугольникаСкачать

👉 ФОРМУЛА ГЕРОНА. Площадь треугольника #shortsСкачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

🔴 Сторона основания правильной треугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

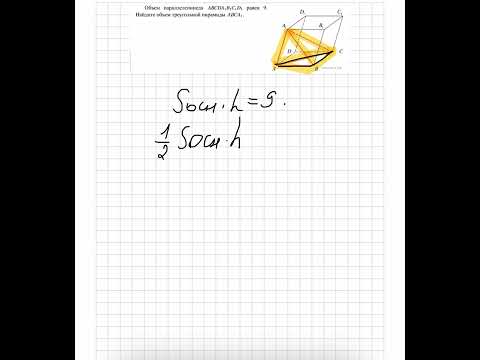
Объем параллелепипеда ABCDA_1B_1C_1D_1 равен 9. Найдите объем треугольной пирамиды ABCA_1.Скачать