Как найти наибольший периметр треугольника

Периметр любого треугольника – это длина линии, ограничивающей фигуру. Чтобы его вычислить, нужно узнать сумму всех сторон этого многоугольника.

Видео:Как вычислить периметр #геометрия #задача #треугольник #периметрСкачать

Вычисление по данным значениям длины сторон

Когда известны их значения, то сделать это несложно. Обозначив эти параметры буквами m, n, k, а периметр буквой P, получим формулу для вычисления: P = m+n+k. Задание: Известно, что треугольник имеет стороны длиной 13,5 дециметров, 12,1 дециметров и 4,2 дециметра. Узнать периметр. Решаем: Если стороны данного многоугольника — a = 13,5 дм, b = 12,1 дм, c = 4,2 дм, то P = 29,8 дм. Ответ: P = 29,8 дм.

Видео:КАК НАЙТИ ПЕРИМЕТР ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Периметр треугольника, который имеет две равные стороны

Такой треугольник называется равнобедренным. Если эти равные стороны имеют длину a сантиметров, а третья сторона – b сантиметров, то периметр легко узнать: P =b+2a. Задание: треугольник имеет две стороны по 10 дециметров, основание 12 дециметров. Найти P. Решение: Пусть боковая сторона a = c = 10 дм, основание b = 12 дм. Сумма сторон P = 10 дм + 12 дм + 10 дм = 32 дм. Ответ: P = 32 дециметра.

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Периметр равностороннего треугольника

Если все три стороны треугольника имеют равное количество единиц измерения, он называется равносторонним. Еще одно название – правильный. Периметр правильного треугольника находят при помощи формулы: P = a+a+a = 3·a. Задача: Имеем равносторонний треугольный земельный участок. Одна сторона равна 6 метрам. Найти длину забора, которым можно обнести этот участок. Решение: Если сторона этого многоугольника a= 6м, то длина забора P = 3·6 = 18 (м). Ответ: P = 18 м.

Видео:Как найти периметр?Скачать

Треугольник, у которого есть угол 90°

Его называют прямоугольным. Наличие прямого угла дает возможность находить неизвестные стороны, пользуясь определением тригонометрических функций и теоремой Пифагора. Самая длинная сторона называется гипотенуза и обозначается c. Имеются еще две стороны, a и b. Следуя теореме, носящей имя Пифагора, имеем c 2 = a 2 + b 2 . Катеты a = √ (c 2 – b 2 ) и b = √ (c 2 – а 2 ). Зная длину двух катетов a и b, вычисляем гипотенузу. Затем находим сумму сторон фигуры, сложив эти значения. Задание: Катеты прямоугольного треугольника имеют длину 8,3 сантиметра и 6,2 сантиметра. Периметр треугольника нужно вычислить. Решаем: Обозначим катеты a = 8,3 см, b = 6,2 см. За теоремой Пифагора гипотенуза c = √ (8,3 2 + 6,2 2 ) = √ (68,89 + 38,44) = √107,33 = 10,4 (см). P = 24,9 (см). Или P = 8,3 + 6,2 + √ (8,3 2 + 6,2 2 ) = 24,9 (см). Ответ: P = 24,9 см. Значения корней брали с точностью до десятых. Если нам известны значения гипотенузы и катета, то значение Р получим, вычислив Р=√ (c 2 – b 2 ) + b + c. Задача 2: Отрезок земельного участка, лежащий против угла в 90 градусов, 12 км, один из катетов – 8 км. За какое время можно обойти весь участок, если двигаться со скоростью 4 километра в час? Решение: если наибольший отрезок — 12 км, меньший b = 8 км, то длина всего пути составит P = 8 + 12 + √ (12 2 – 8 2 ) = 20 + √80 = 20 + 8,9 = 28,9 (км). Время найдем, разделив путь на скорость. 28,9:4 = 7,225 (ч). Ответ: можно обойти за 7,3 ч. Значение квадратных корней и ответа берем с точностью до десятых. Можно найти сумму сторон прямоугольного треугольника, если дана одна из сторон и значение одного из острых углов. Зная длину катета b и значение противолежащего ему угла β, найдем неизвестную сторону a = b/ tg β. Находим гипотенузу c = a: sinα. Периметр такой фигуры находим, сложив полученные значения. P = a + a/ sinα + a/ tg α, или P = a(1 / sin α+ 1+1 / tg α). Задание: В прямоугольном Δ АВС с прямым углом С катет ВС имеет длину 10 м, угол А – 29 градусов. Нужно найти сумму сторон Δ АВС. Решение: Обозначим известный катет ВС = a = 10 м, угол, лежащий напротив него, ∟А = α = 30°, тогда катет АС = b = 10: 0,58 = 17,2 (м), гипотенуза АВ = c = 10: 0,5 = 20 (м). Р = 10 + 17,2 + 20 = 47,2 (м). Или Р = 10 · (1 + 1,72 + 2) = 47,2 м. Имеем: P = 47,2 м. Значение тригонометрических функций берем с точностью до сотых, значение длины сторон и периметра округляем до десятых. Имея значение катета α и прилежащего угла β, узнаем, чему равен второй катет: b = a tg β. Гипотенуза в таком случае будет равна катету, разделенному на косинус угла β. Периметр узнаем по формуле P = a + a tg β + a: cos β = (tg β + 1+1: cos β)·a. Задание: Катет треугольника с углом 90 градусов 18 см, прилежащий угол – 40 градусов. Найти P. Решение: Обозначим известный катет ВС = 18 см, ∟β = 40°. Тогда неизвестный катет АС = b = 18 · 0,83 = 14,9 (см), гипотенуза АВ = c = 18: 0,77 = 23,4 (см). Сумма сторон фигуры равна Р = 56,3 (см). Или Р = (1 + 1,3+0,83)*18 = 56,3 см. Ответ: P = 56,3 см. Если известна длина гипотенузы c и какой-нибудь угол α, то катеты будут равны произведению гипотенузы для первого – на синус и для второго – на косинус этого угла. Периметр этой фигуры P = (sin α + 1+ cos α)*c. Задание: Гипотенуза прямоугольного треугольника АВ = 9,1 сантиметр, а угол 50 градусов. Найти сумму сторон данной фигуры. Решение: Обозначим гипотенузу: AB = c = 9,1 см, ∟A= α = 50°, тогда один из катетов BC имеет длину a = 9,1 · 0,77 = 7 (см), катет АС = b = 9,1 · 0,64 = 5,8 (см). Значит периметр этого многоугольника равен P = 9,1 + 7 + 5,8 = 21,9 (см). Или P = 9,1·(1 + 0,77 + 0,64) = 21,9 (см). Ответ: P = 21,9 сантиметров.

Видео:Найдите периметр треугольникаСкачать

Произвольный треугольник, одна из сторон которого неизвестна

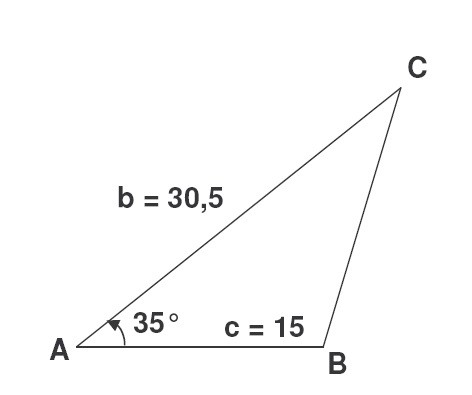
Если мы имеем значения двух сторон a и c, и угла между этими сторонами γ, третью находим теоремой косинусов: b 2 = с 2 + a 2 – 2 ас cos β, где β – угол, лежащий между сторонами а и с. Затем находим периметр. Задание: Δ АВС имеет отрезок АВ длиной 15 дм, отрезок АС, длина которго 30,5 дм. Значение угла между этими сторонами 35 градусов. Вычислить сумму сторон Δ АВС. Решение: Теоремой косинусов вычислим длину третей стороны. BC 2 = 30,5 2 + 15 2 — 2·30,5·15·0,82 = 930,25 + 225 – 750,3 = 404,95. BC = 20,1 см. P = 30,5 + 15 + 20,1 = 65,6 (дм).Имеем: P = 65,6 дм.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Сумма сторон произвольного треугольника, у которого длины двух сторон неизвестны

Когда знаем длину только одного отрезка и значение двух углов, можно узнать длину двух неизвестных сторон, пользуясь теоремой синусов: «в треугольнике стороны всегда пропорциональны значениям синусов противоположных углов». Откуда b = (a* sin β)/ sin a. Аналогично c = (a sin γ): sin a. Периметр в таком случае будет P = а + (а sin β)/ sin a + (a sin γ)/ sin a. Задание: Имеем Δ ABC. В нем длина стороны BC 8,5 мм, значение угла C – 47°, а угла B – 35 градусов. Найти сумму сторон данной фигуры. Решение: Обозначим длины сторон BC = a = 8,5 мм, AC = b, AB = c, ∟ A = α= 47°, ∟B = β = 35°, ∟ C = γ = 180° – (47° + 35°) = 180° – 82° = 98°. Из соотношений, полученных из теоремы синусов, находим катеты AC = b = (8,5·0,57): 0,73= 6,7 (мм), AB = c = (7 · 0,99): 0,73 = 9,5 (мм). Отсюда сумма сторон этого многоугольника равна P = 8,5 мм + 5,5 мм + 9,5 мм = 23,5 мм. Ответ: P = 23,5 мм. В случае, когда есть только длина одного отрезка и значения двух прилежащих углов, сначала вычисляем угол, противоположный известной стороне. Все углы этой фигуры в сумме имеют 180 градусов. Поэтому ∟A = 180° — (∟B + ∟C). Дальше находим неизвестные отрезки, используя теорему синусов. Задание: Имеем Δ ABC. Он имеет отрезок BC, равный 10 см. Значение угла B равно 48 градусов, угол C равен 56 градусов. Найти сумму сторон Δ ABC. Решение: Сначала найдем значение угла A, противолежащего стороне BC. ∟A = 180° – (48° + 56°) = 76°. Теперь с теоремой синусов вычислим длину стороны AC = 10·0,74: 0,97 = 7,6 (см). AB = BC* sin C/ sin A = 8,6. Периметр треугольника Р = 10 + 8,6 + 7,6 = 26,2 (см). Результат: P = 26,2 см.

Видео:Урок. Как найти периметр треугольника. Математика 2 класс. #учусьсамСкачать

Вычисление периметра треугольника с использованием радиуса окружности, вписанной в него

Иногда из условия задачи не известна ни одна сторона. Зато есть значение площади треугольника и радиуса окружности, вписанной в него. Эти величины связаны: S = r p. Зная значение площади треугольника, радиуса r, можем найти полупериметр p. Находим p = S: r. Задача: Участок имеет площадь 24 м 2 , радиус r равен 3 м. Найти количество деревьев, которое нужно высадить равномерно по линии, ограждающей этот участок, если между двумя соседними должно быть расстояние 2 метра. Решение: Сумму сторон данной фигуры находим так: P = 2 · 24: 3 = 16 (м). Затем делим на два. 16:2= 8. Итого: 8 деревьев.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Сумма сторон треугольника в декартовых координатах

Вершины Δ АВС имеют координаты: A (x₁; y₁), B (x₂; y₂), C(x₃ ; y₃). Найдем квадраты каждой из сторон AB 2 = (x₁ — x₂) 2 + (y₁ — y₂) 2 ; ВС 2 = (x₂ — x₃) 2 + (y₂ — y₃) 2 ; АС 2 = (x₁ — x₃) 2 + (y₁ — y₃) 2 . Чтобы найти периметр, достаточно сложить все отрезки. Задание: Координаты вершин Δ ABC: B (3; 0), A (1; -3), C (2; 5). Найти сумму сторон этой фигуры. Решение: поставив значения соответствующих координат в формулу периметра, получим P = √(4 + 9) + √(1 + 25) + √(1 + 64) = √13 + √26 + √65 = 3,6 + 5,1 + 8,0 = 16,6. Имеем: P = 16,6. Если фигура находится не на плоскости, а в пространстве, то каждая из вершин имеет три координаты. Поэтому формула суммы сторон будет иметь еще одно слагаемое.

Видео:Математика 2 класс. «Периметр треугольника, прямоугольника и квадрата»Скачать

Векторный метод

Если фигура задана координатами вершин, периметр можно вычислить, используя векторный метод. Вектор – отрезок, имеющий направление. Его модуль (длина) обозначается символом ǀᾱǀ. Расстояние между точками – это и есть длина соответствующего вектора, или модуль вектора. Рассмотрим треугольник, лежащий на плоскости. Если вершины имеют координаты А (х₁; у₁), М(х₂; у₂), Т (х₃; у₃), то длину каждой из сторон находим по формулам: ǀАМǀ = √ ((х₁ – х₂) 2 + (у₁ – у₂) 2 ), ǀМТǀ = √ ((х₂ – х₃) 2 + (у₂ – у₃) 2 ), ǀАТǀ = √ ((х₁ – х₃) 2 + (у₁ – у₃) 2 ). Периметр треугольника получим, сложив длины векторов. Аналогично находят сумму сторон треугольника в пространстве.

Видео:Как найти периметрСкачать

Как найти периметр треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

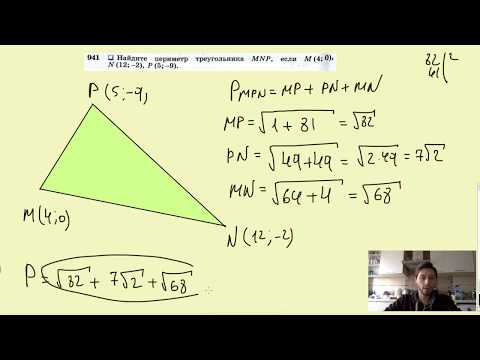
Видео:№941. Найдите периметр треугольника MNP, если М (4; 0), N(12; -2), В (5; -9).Скачать

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Видео:Задачи на периметр труегольника. Геометрия 7 класс. Две задачи.Скачать

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Видео:Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Максимальный периметр треугольника из массива

Дан Массив неотрицательных целых чисел. Найдите три элемента из этого массива, которые образуют треугольник с максимальным периметром.

Примеры :

Наивное решение:
Решение по грубой силе: проверить для всех комбинаций из 3 элементов, образует ли он треугольник или нет, и обновить максимальный периметр, если он образует треугольник. Сложность наивного решения составляет O (n 3 ). Ниже приведен код для этого.

// Решение грубой силы, чтобы найти
// вне максимального периметра треугольника, который
// может быть сформирован с использованием элементов
// данного массива
#include
#include

using namespace std;

// Функция для определения максимального периметра

void maxPerimeter( int arr[], int n)<

// инициализируем максимальный периметр

// подбираем 3 разных элемента

for ( int i = 0; i

for ( int j = i + 1; j

for ( int k = j + 1; k

// a, b, c — 3 стороны треугольника

// проверяем, формируются ли a, b, c

// треугольник или нет.

// если он образует треугольник

// затем обновляем максимальное значение.

maxi = max(maxi, a+b+c);

// Если максимальный периметр ненулевой

// затем распечатать его.

if (maxi) cout «Maximum Perimeter is: «

// иначе треугольник не образуется

else cout «Triangle formation «

«is not possible.»

// Программа для водителя

// тестовый пример 1

// контрольный пример 2

// тестовый пример 3

// Решение грубой силы, чтобы узнать максимум
// треугольник периметра, который может быть сформирован
// используя элементы данного массива

// Функция для определения максимального периметра

static void maxPerimeter( int arr[], int n)

// инициализируем максимальный периметр как 0.

// подбираем 3 разных элемента

for ( int i = 0 ; i 2 ; i++)

for ( int j = i + 1 ; j 1 ; j++)

for ( int k = j + 1 ; k

// a, b, c — 3 стороны

// проверяем, a, b, c

// образует треугольник или нет.

// если он образует треугольник

// затем обновляем максимум

maxi = Math.max(maxi, a+b+c);

// Если максимальный периметр ненулевой

// затем распечатать его.

System.out.println( «Maximum Perimeter is: «

// иначе треугольник не образуется

System.out.println( «Triangle formation «

+ «is not possible.» );

// Программа для водителя

public static void main (String[] args)

// тестовый пример 1

// контрольный пример 2

// тестовый пример 3

12 , 5 , 55 , 4 , 9 >;

// Этот код предоставлен anuj_67.

# Решение грубой силы, чтобы найти
№ из максимального периметра треугольника
# который может быть сформирован с использованием
# элементы данного массива

# Функция, чтобы узнать
# максимальный периметр

# подобрать 3 разных

# элементы из массива.

for i in range (n — 2 ):

for j in range (i + 1 , n — 1 ):

for k in range (j + 1 , n):

# a, b, c — 3 стороны

if (a + c and b + c

maxi = max (maxi, a + b + c)

return «Triangle formation is not possible»

return «Maximum Perimeter is: » + str (maxi)

arr1 = [ 6 , 1 , 6 , 5 , 8 , 4 ]

arr2 = [ 2 , 20 , 7 , 55 ,

arr3 = [ 33 , 6 , 20 , 1 , 8 ,

12 , 5 , 55 , 4 , 9 ]

if __name__ = = ‘__main__’ :

# Этот код добавлен
# Прита Updhayay

// Решение грубой силы, чтобы узнать
// максимальный периметр треугольника, который
// может быть сформирован с использованием элементов
// данного массива

// Функция, чтобы узнать

static void maxPerimeter( int []arr,

// подбираем 3 разных элемента

for ( int i = 0; i

for ( int j = i + 1; j

for ( int k = j + 1; k

// a, b, c — 3 стороны

// проверяем, a, b, c

// образует треугольник или нет.

// если он образует треугольник

// затем обновляем максимум

maxi = Math.Max(maxi, a + b + c);

// Если максимальный периметр

// не ноль, затем распечатать его.

Console.WriteLine( «Maximum Perimeter is: » + maxi);

// иначе треугольника нет

Console.WriteLine( «Triangle formation » +

«is not possible.» );

public static void Main ()

// тестовый пример 1

// контрольный пример 2

// тестовый пример 3

// Этот код предоставлен anuj_67.

// Решение грубой силы, чтобы найти
// вне максимального периметра треугольника, который
// может быть сформирован с использованием элементов
// данного массива

// Функция, чтобы узнать
// максимальный периметр

function maxPerimeter( $arr , $n )

// подбираем 3 разных

// элементы из массива.

for ( $i = 0; $i $n — 2; $i ++)

for ( $j = $i + 1; $j $n — 1; $j ++)

for ( $k = $j + 1; $k $n ; $k ++)

// a, b, c — 3 стороны

// проверяем, a, b, c

// образует треугольник или нет.

// если он образует треугольник

// затем обновляем максимальное значение.

$maxi = max( $maxi , $a + $b + $c );

// Если максимальный периметр

// не ноль, затем распечатать его.

echo «Maximum Perimeter is: » ;

// иначе треугольника нет

echo «Triangle formation » ;

echo «is not possible. n» ;

// тестовый пример 1

$arr1 = array (6, 1, 6, 5, 8, 4);

maxPerimeter( $arr1 , 6);

// контрольный пример 2

$arr2 = array (2, 20, 7, 55,

maxPerimeter( $arr2 , 8);

// тестовый пример 3

$arr3 = array (33, 6, 20, 1, 8,

maxPerimeter( $arr3 , 10);

// Этот код предоставлен anuj_67.
?>

Выход :

Эффективный подход:
Сначала мы можем отсортировать массив по возрастанию. Итак, первый элемент будет максимальным, а последний будет минимальным. Теперь, если первые 3 элемента этого отсортированного массива образуют треугольник, это будет треугольник с максимальным периметром, так как для всех других комбинаций сумма элементов (то есть периметр этого треугольника) будет = b> = c). a, b, c не могут образовывать треугольник, поэтому a> = b + c. As, b и c = c + d (если мы отбросим b и возьмем d) или a> = b + d (если мы отбросим c и возьмем d). Итак, мы должны бросить и забрать д.
Опять же набор анализа для b, c и d. Мы можем продолжать это до последнего и всякий раз, когда мы находим треугольник, образующий тройку, мы можем прекратить проверку, так как эта тройка дает максимальный периметр.
Следовательно, если в отсортированном массиве arr [i] Ниже приведена простая реализация этой концепции:

// Эффективное решение для поиска
// вне максимального периметра треугольника, который
// может быть сформирован с использованием элементов
// данного массива
#include
#include

using namespace std;

// Функция для определения максимального периметра

void maxPerimeter( int arr[], int n)<

// сортируем элементы массива

// в обратном порядке

sort(arr, arr+n, greater int >());

// цикл через отсортированный массив

// и проверяем, образует ли он

// треугольник или нет.

for ( int i = 0; i

// Проверяем, есть ли arr [i], arr [i + 1]

// и arr [i + 2] образует треугольник

// если он образует треугольник

// это треугольник с

maxi = max(maxi, arr[i] + arr[i+1] + arr[i+2]);

// Если максимальный периметр ненулевой

// затем распечатать его.

cout «Maximum Perimeter is: «

// иначе треугольник не образуется

cout «Triangle formation»

«is not possible.»

// Программа для водителя

// тестовый пример 1

// контрольный пример 2

// тестовый пример 3

// Эффективное решение для поиска
// вне максимального периметра треугольника, который
// может быть сформирован с использованием элементов
// данного массива

// Функция для определения максимального периметра

static void maxPerimeter( int arr[], int n) <

// сортируем элементы массива

// в обратном порядке

// сортировать (arr, arr + n, больше ());

// цикл через отсортированный массив

// и проверяем, образует ли он

// треугольник или нет.

for ( int i = 0 ; i 2 ; i++) <

// Проверяем, есть ли arr [i], arr [i + 1]

// и arr [i + 2] образует треугольник

if (arr[i] 1 ] + arr[i + 2 ]) <

// если он образует треугольник

// это треугольник с

maxi = Math.max(maxi, arr[i] + arr[i + 1 ] + arr[i + 2 ]);

// Если максимальный периметр ненулевой

// затем распечатать его.

System.out.println( «Maximum Perimeter is: » + maxi);

> // иначе треугольник не образуется

System.out.println( «Triangle formation is not possible.» );

// Функция возвращает отсортированный массив по убыванию

static int [] arrRevSort( int [] arr) <

Arrays.sort(arr, 0 , arr.length);

int j = arr.length — 1 ;

for ( int i = 0 ; i 2 ; i++, j—) <

// Программа для водителя

public static void main(String[] args) <

// тестовый пример 1

// контрольный пример 2

// тестовый пример 3

>
/ * Этот Java-код предоставлен 29AjayKumar * /

# Эффективное решение, чтобы найти
№ из максимального периметра треугольника, который
# может быть сформирован с использованием элементов
# данного массива

# Функция для поиска
# максимальный периметр

for i in range ( 0 , n — 2 ):

if arr[i] + 1 ] + arr[i + 2 ]):

maxi = max (maxi, arr[i] +

arr[i + 1 ] + arr[i + 2 ])

return «Triangle formation is not possible»

return «Maximum Perimeter is: » + str (maxi)

arr1 = [ 6 , 1 , 6 , 5 , 8 , 4 ]

arr2 = [ 2 , 20 , 7 , 55 ,

arr3 = [ 33 , 6 , 20 , 1 , 8 ,

12 , 5 , 55 , 4 , 9 ]

if __name__ = = ‘__main__’ :

# Этот код добавлен
# Прита Упадхяй

// Эффективное решение для поиска
// вне максимального периметра треугольника, который
// может быть сформирован с использованием элементов
// данного массива

// Функция для определения максимального периметра

static void maxPerimeter( int [] arr, int n) <

// сортируем элементы массива

// в обратном порядке

// сортировать (arr, arr + n, больше ());

// цикл через отсортированный массив

// и проверяем, образует ли он

// треугольник или нет.

for ( int i = 0; i

// Проверяем, есть ли arr [i], arr [i + 1]

// и arr [i + 2] образует треугольник

// если он образует треугольник

// это треугольник с

maxi = Math.Max(maxi, arr[i] + arr[i + 1] + arr[i + 2]);

// Если максимальный периметр ненулевой

// затем распечатать его.

Console.WriteLine( «Maximum Perimeter is: » + maxi);

> // иначе треугольник не образуется

Console.WriteLine( «Triangle formation is not possible.» );

// Функция возвращает отсортированный массив по убыванию

static int [] arrRevSort( int [] arr) <

int j = arr.Length — 1;

for ( int i = 0; i

// Программа для водителя

public static void Main() <

// тестовый пример 1

// контрольный пример 2

// тестовый пример 3

>
/ * Этот код Java предоставлен mits * /

// Эффективное решение, чтобы узнать максимум
// треугольник периметра, который может быть сформирован
// используя элементы данного массива

// Функция для определения максимального периметра

function maxPerimeter(& $arr , $n )

// сортируем элементы массива в

// инициализируем максимальный периметр до 0

// цикл через отсортированный массив

// и проверяем, образует ли он

// треугольник или нет.

for ( $i = 0; $i $n — 2; $i ++)

// Проверяем, есть ли arr [i], arr [i + 1]

// и arr [i + 2] образует треугольник

if ( $arr [ $i ] $arr [ $i + 1] +

// если он образует треугольник

// это треугольник с

$maxi = max( $maxi , $arr [ $i ] +

// Если максимальный периметр ненулевой

// затем распечатать его.

echo ( «Maximum Perimeter is: » );

// иначе треугольник не образуется

echo ( «Triangle formation » );

echo ( «is not possible.» );

// тестовый пример 1

$arr1 = array (6, 1, 6, 5, 8, 4);

maxPerimeter( $arr1 , $s );

// контрольный пример 2

$arr2 = array (2, 20, 7, 55, 1,33, 12, 4);

$st = sizeof( $arr2 );

maxPerimeter( $arr2 , $st );

// тестовый пример 3

$arr3 = array (33, 6, 20, 1, 8,

$st1 = sizeof( $arr3 );

maxPerimeter( $arr3 , $st1 );

// Этот код добавлен
// от Shivi_Aggarwal
?>

Выход :

Временная сложность такого подхода составляет O (n * log (n)). Это много времени требуется для сортировки массива.

💡 Видео

Как найти площадь треугольника без формулы?Скачать

Найдите сторону треугольника на рисункеСкачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Что такое периметр. Как найти периметр многоугольника?Скачать

Высота, биссектриса, медиана. 7 класс.Скачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать