Как найти матрицу грама системы векторов (2 видео)

VMath

Содержание

Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Матрица и определитель Грама
Линейная независимость векторов
Свойства определителя Грама
Расстояние до линейного многообразия
Объемы параллелепипедов
Матрица и определитель Грама: определение, свойства, приложения
Определение матрицы Грама
Изменение матрицы Грама при переходе от одного базиса к другому
Определитель Грама и его свойства
Метрические приложения определителя Грама
33. Матрица Грама в евклидовом пространстве
📸 Видео

Инструменты сайта

Основное

Информация

Действия

Содержание

Вспомогательная страница к разделу ЕВКЛИДОВО ПРОСТРАНСТВО

Видео:A.7.4 Ортогонализация набора векторов. Процесс Грама-Шмидта.Скачать

Матрица и определитель Грама

Пусть в евклидовом пространстве $ mathbb E_ $ известным образом задано скалярное произведение $ langle X_,Y rangle $. Матрицей Грама системы векторов $ <X_,dots,X_m > $ называется квадратная матрица, состоящая из всевозможных скалярных произведений этих векторов: $$ G(X_1,dots,X_m)= left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right) = left[ langle X_j,X_k rangle right]_^m . $$ Матрица Грама является симметричной матрицей. Ее определитель называется определителем Грама (или грамианом) системы векторов $ <X_,dots,X_m > $: $$ (X_1,dots,X_m)=left| begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right| = det left[ langle X_j,X_k rangle right]_^m . $$

Пример. Если в пространстве $ mathbb R^ $ строк, состоящих из $ n_ $ вещественных чисел, скалярное произведение определяется по правилу 1)

$$ langle X,Y rangle=x_1y_1+x_2y_2+dots+x_ny_n quad npu quad X=(x_1,x_2,dots,x_n), Y=(y_1,y_2,dots,y_n) , $$ то матрица Грама строк $$ X_1=left(x_,x_,dots, x_right),dots,X_m=left(x_,x_,dots, x_right) $$ вычисляется перемножением матриц: $$ G(X_1,dots,X_m)=Xcdot X^ quad npu quad X= left(begin x_ & x_ &dots & x_ \ dots & & & dots \ x_& x_ & dots & x_ end right) $$ и при $ ^_ $ означающем транспонирование. Из теоремы Бине-Коши немедленно следует, что при $ m>n_ $ (числе строк превышающем размерность пространства) определитель Грама равен нулю. Этот результат обобщен НИЖЕ для произвольных евклидовых пространств.

Пример. Если в пространстве полиномов с вещественными коэффициентами скалярное произведение задано формулой

$$ langle p(x),q(x) rangle =int_0^1 p(t) q(t) d,t ,$$ то $$ G(1,x,x^2)= left( begin int_0^1 1 d,t & int_0^1 t d,t & int_0^1 t^2 d,t \ & & \ int_0^1 t d,t & int_0^1 t^2 d,t & int_0^1 t^3 d,t \ & & \ int_0^1 t^2 d,t & int_0^1 t^3 d,t & int_0^1 t^4 d,t end right)= left( begin 1 & 1/2 & 1/3 \ 1/2 & 1/3 & 1/4 \ 1/3 & 1/4 & 1/5 end right) . $$ Обобщение получившейся матрицы известно как матрица Гильберта.

Если система векторов $ <X_,dots,X_n > $ образует базис пространства $ mathbb E_ $ (т.е. пространство $ mathbb E_ $ является $ n_ $-мерным), то задание матрицы Грама $ G(X_,dots,X_n) $ позволяет свести вычисление скалярного произведения произвольных векторов из $ mathbb E_ $ к действиям над их координатами: $$ X=x_1X_1+x_2X_2+dots+x_nX_n, Y=y_1X_1+y_2X_2+dots+y_nX_n Rightarrow $$ $$ langle X,Y rangle=left(x_1,x_2,dots,x_n right) left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \ dots & & & dots \ langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle end right) left( begin y_1 \ y_2 \ vdots \ y_n end right) . $$

Видео:№4. "Найти матрицу Грама системы векторов, если скалярное произведение..." Алгебра и геометрия.Скачать

Линейная независимость векторов

Теорема. $ (X_,dots,X_m)=0 $ тогда и только тогда, когда система векторов $ <X_,dots,X_m > $ линейно зависима.

Доказательство ☞ ЗДЕСЬ.

Если какой-то главный минор матрицы Грама обращается в нуль, то и все главные миноры бóльших порядков обращаются в нуль.

Видео:Матрица ГрамаСкачать

Свойства определителя Грама

Теорема. $ (X_,dots,X_m) ge 0 $ для любой системы векторов $ <X_,dots,X_m > $.

Доказательство ☞ ЗДЕСЬ

При $ m=2_ $ получаем неравенство Коши-Буняковского: $$ langle X_1,X_1 rangle cdot langle X_2,X_2 rangle ge langle X_1,X_2 rangle^2 . $$

Матрица Грама линейно независимой системы векторов является положительно определенной.

Доказательство ☞ ЗДЕСЬ

Величина определителя Грама не превосходит его главного члена, т.е. произведения элементов его главной диагонали:

Для произвольной квадратной вещественной матрицы

$$A=left( begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots & & & dots \ a_ & a_ & dots & a_ end right) $$ справедливо неравенство Адамара 2) : $$ left| det A right| le sqrt< sum_^n a_^2> sqrt< sum_^n a_^2> times dots times sqrt< sum_^n a_^2> . $$ Иными словами: модуль определителя матрицы не превосходит произведения длин его строк. Аналогичное утверждение справедливо и относительно столбцов матрицы.

Доказательство. Обозначим $ j_ $-ю строку матрицы $ A_ $ через $ A^ $. Тогда, поскольку $ det A= det A^ $ (см. свойство 1 ☞ ЗДЕСЬ ), имеем: $$left( det A right)^2= det left(Acdot A^ right)= det left[ begin langle A^,A^ rangle & langle A^,A^ rangle & dots & langle A^,A^ rangle \ langle A^,A^ rangle & langle A^,A^ rangle & dots & langle A^,A^ rangle \ dots & & & dots \ langle A^,A^ rangle & langle A^,A^ rangle & dots & langle A^,A^ rangle end right]= $$ $$ =mathfrakleft(A^,A^,dots,A^ right) $$ при задании скалярного произведения в $ mathbb R^n $ стандартным способом. На основании предыдущего следствия, имеем: $$ le left|A^ right|^2 left|A^ right|^2 times dots times left|A^ right|^2 . $$ Равенство возможно тогда и только тогда, когда либо все строки попарно ортогональны, либо хотя бы одна строка — нулевая. ♦

Пример.

$$ left|detleft( begin -47 & 40 & -81 \ 91 & 68 & -10 \ 31 & -51 & 77 end right) right| le $$ $$ le left< begin sqrt &le 1131360 \ & \ sqrt & le 1127957 end right. $$ при точной величине определителя $ 31867 $.

Теорема. Величина определителя Грама не изменится, если к системе векторов применить алгоритм ортогонализации Грама-Шмидта. В обозначениях этого алгоритма имеет место равенство:

Видео:Процесс ортогонализации Грама-Шмидта. ПримерСкачать

Расстояние до линейного многообразия

Теорема. Расстояние $ d_ $ от точки $ X_ in $ до линейного многообразия в $ mathbb E_ $

Доказательство для случая $ Y_0=mathbb O_ $ ☞ ЗДЕСЬ. Случай $ Y_ne mathbb O $ сводится к предыдущему сдвигом пространства на вектор $ (- Y_) $: см. комментарии к теореме $ 3_ $ ☞ ЗДЕСЬ. ♦

Другие применения определителя Грама в задачах вычисления расстояний между поверхностями в $ ^ $ ☞ ЗДЕСЬ.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Объемы параллелепипедов

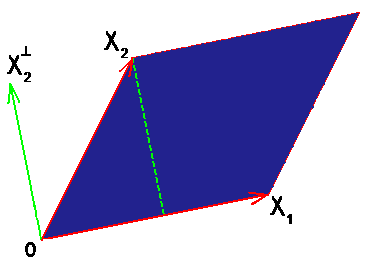
Площадь параллелограмма равна произведению его основания на высоту. Если параллелограмм построен на векторах $ X_ $ и $ X_2 $ из $ mathbb R^2 $, то за основание можно принять длину вектора $ X_ $, а за высоту — длину перпендикуляра, опущенного из конца вектора $ X_2 $ на ось вектора $ X_ $.

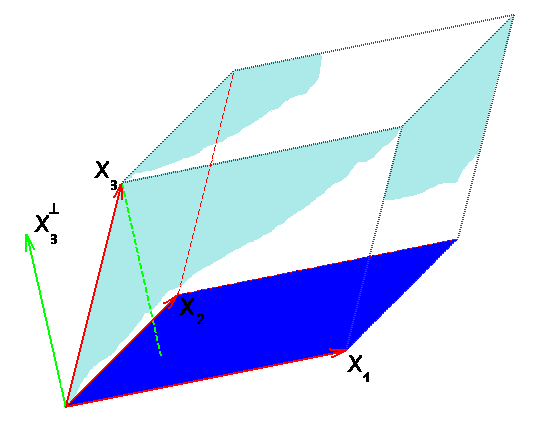
Аналогично, объем параллелепипеда, построенного на векторах $ X_1,X_2,X_3 $ из $ mathbb R^ $, равен произведению площади основания на высоту; площадь основания — это площадь параллелограмма, построенного на векторах $ X_1,X_2 $, а высота — длина перпендикуляра, опущенного из конца вектора $ X_3 $ на плоскость векторов $ X_1,X_2 $.

Объем $ k_ $-мерного параллелепипеда в евклидовом пространстве $ mathbb E_ $ определим по индукции. Если этот параллелепипед построен на векторах $ X_1,X_2,dots,X_,X_k $, то за его объем примем произведение объема $ (k-1) $-мерного параллелепипеда, построенного на векторах $ X_1,X_2,dots,X_ $ на длину перпендикуляра, опущенного из точки $ X_ $ на линейную оболочку векторов $ X_1,X_2,dots,X_ $ (т.е. на длину ортогональной составляющей $ X_k $ относительно $ mathcal L ( X_1,X_2,dots,X_) $): $$mathbf V(X_1,X_2,dots,X_,X_k)=left|X_k^ right| mathbf V(X_1,X_2,dots,X_) . $$

Теорема. Квадрат объема параллелепипеда, построенного на векторах $ X_1,X_2,dots,X_k $, совпадает с величиной определителя Грама от той же системы векторов: $$[V(X_1,X_2,dots,X_k)]^2= mathfrak G (X_1,X_2,dots,X_k) .$$

Доказательство следует из представления длины ортогональной составляющей $ X_k^<^> $ через определители Грама (см. теорему $ 2_ $ и следствие к ней ☞ ЗДЕСЬ ).

Модуль определителя вещественной матрицы

$$ A= left( begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots & & & dots \ a_ & a_ & dots & a_ end right) $$ равен объему параллелепипеда в пространстве $ mathbb R^_ $, построенного на вершинах с координатами $$ (0,0,dots, 0), (a_,a_, dots , a_),(a_,a_, dots , a_), dots, (a_,a_, dots, a_) $$ (т.е. «построенного на строках матрицы») и равен объему параллелепипеда построенного на вершинах с координатами $$ (0,0,dots, 0), (a_,a_, dots , a_),(a_,a_, dots , a_), dots, (a_,a_, dots, a_) $$ (т.е. «построенного на столбцах матрицы»).

Доказательство фактически совпадает с доказательством неравенства Адамара: $$ left(det A right)^2 = left< begin det left(A cdot A^right)=mathfrak G (A^,A^,dots,A^) &= left[mathbf V(A^,A^,dots,A^)right]^2 \ & \ det left(A^ cdot A right) = mathfrak G (A_,A_,dots,A_) & = left[mathbf V(A_,A_,dots,A_)right]^2 end right. $$ ♦

Видео:Матрицы и векторыСкачать

Матрица и определитель Грама: определение, свойства, приложения

Видео:Как разложить вектор по базису - bezbotvyСкачать

Определение матрицы Грама

Квадратная симметрическая матрица [math]G(mathbf_1,mathbf_2,ldots, mathbf_n)[/math] , составленная из скалярных произведений системы векторов [math]mathbf_1,mathbf_2, ldots, mathbf_n[/math] называется матрицей Грама

Видео:Лекция 5.7. Ортогонализация Грама-Шмидта: примерСкачать

Изменение матрицы Грама при переходе от одного базиса к другому

Пусть [math](mathbf)=(mathbf_1,ldots,mathbf_n)[/math] и [math](mathbf)= (mathbf_1,ldots,mathbf_n)[/math] — два базиса евклидова пространства [math]mathbb[/math] , a [math]S[/math] — матрица перехода от базиса [math](mathbf)[/math] к базису [math](mathbf)colon, (mathbf)=(mathbf)S[/math] . Требуется найти связь матриц Грама систем векторов [math](mathbf)[/math] и [math](mathbf)[/math]

По формуле (8.32) вычислим скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] в разных базисах:

где [math]mathoplimits_<(mathbf)>,, mathoplimits_<(mathbf)>[/math] и [math]mathoplimits_<(mathbf)>,, mathoplimits_<(mathbf)>[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] в соответствующих базисах. Подставляя в последнее равенство связи [math]mathoplimits_<(mathbf)>= S mathoplimits_<(mathbf)>,[/math] [math]mathoplimits_<(mathbf)>= S mathoplimits_<(mathbf)>[/math] , получаем тождество

Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому :

Записав это равенство для ортонормированных базисов [math](mathbf)[/math] и [math](mathbf)[/math] , получаем [math]E=S^TES[/math] , так как матрицы Грама ортонормированных базисов единичные: [math]G(mathbf_1,ldots,mathbf_n)= G(mathbf_1,ldots,mathbf_n)=E[/math] . Поэтому матрица [math]S[/math] перехода от одного ортонормированного базиса к другому является ортогональной: [math]S^=S^T[/math] .

Видео:Линал 5.6. Матрица ГрамаСкачать

Определитель Грама и его свойства

Определитель матрицы [math]G(mathbf_1,mathbf_2,ldots, mathbf_n)[/math] называется определителем Грама. Рассмотрим свойства этого определителя.

1. Критерий Грама линейной зависимости векторов: система векторов [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима тогда и только тогда, когда определитель Грама этой системы равен нулю.

Действительно, если система [math]mathbf_1, mathbf_2, ldots,mathbf_k[/math] линейно зависима, то существуют такие числа [math]x_1,x_2,ldots,x_k[/math] , не равные нулю одновременно, что

Умножая это равенство скалярно на [math]mathbf_1[/math] , затем на [math]mathbf_2[/math] и т.д. на [math]mathbf_k[/math] , получаем однородную систему уравнений [math]G(mathbf_1,mathbf_2,ldots,mathbf_k)x=o[/math] , которая имеет нетривиальное решение [math]x=beginx_1&cdots&x_k end^T[/math] . Следовательно, ее определитель равен нулю. Необходимость доказана. Достаточность доказывается, проводя рассуждения в обратном порядке.

Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.

Главный минор матрицы Грама системы [math]mathbf_1, mathbf_2,ldots,mathbf_k[/math] представляет собой определитель Грама подсистемы векторов. Если подсистема линейно зависима, то и вся система линейно зависима.

2. Определитель Грама [math]det<G (mathbf_1,mathbf_2, ldots, mathbf_k)>[/math] не изменяется в процессе ортогонализации системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] . Другими словами, если в процессе ортогонализации векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] получены векторы [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] , то

Действительно, в процессе ортогонализации по векторам [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] последовательно строятся векторы

После первого шага определитель Грама не изменяется

Выполним с определителем [math]det G(mathbf_1, mathbf_2, ldots,mathbf_k)[/math] следующие преобразования. Прибавим ко второй строке первую, умноженную на число [math](-alpha_)[/math] , а затем ко второму столбцу прибавим первый, умноженный на [math](-alpha_)[/math] . Получим определитель

Так как при этих преобразованиях определитель не изменяется, то

Значит, после второго шага в процессе ортогонализации определитель не изменяется. Продолжая аналогично, получаем после [math]k[/math] шагов:

Вычислим правую часть этого равенства. Матрица [math]G(mathbf_1,mathbf_2,ldots, mathbf_k)[/math] Грама ортогональной системы [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] векторов является диагональной, так как [math]langle mathbf_i,mathbf_jrangle=0[/math] при [math]ine j[/math] . Поэтому ее определитель равен произведению элементов, стоящих на главной диагонали:

3. Определитель Грама любой системы [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] векторов удовлетворяет двойному неравенству

Докажем неотрицательность определителя Грама. Если система [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима, то определитель равен нулю (по свойству 1). Если же система [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] линейно независима, то, выполнив процесс ортогонализации, получим ненулевые векторы [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] , для которых по свойству 2:

Оценим теперь скалярный квадрат [math]langle mathbf_j,mathbf_jrangle[/math] . Выполняя процесс ортого-1нализации, имеем [math]mathbf_j= mathbf_j+ alpha_mathbf_1+ ldots+ alpha_mathbf_[/math] . Отсюда

Следовательно, по свойству 2 имеем

1. Матрица Грама любой системы векторов является неотрицательно определенной, так как все ее главные миноры также являются определителями Грама соответствующих подсистем векторов и неотрицательны в силу свойства 3.

2. Матрица Грама любой линейно независимой системы векторов является положительно определенной, так как все ее угловые миноры положительны (в силу свойств 1,3), поскольку являются определителями Грама линейно независимых подсистем векторов.

Видео:Процесс ортогонализации Грама-Шмидта. ТемаСкачать

Метрические приложения определителя Грама

Пусть [math]boldsymbol_1,boldsymbol_2, ldots,boldsymbol_k[/math] — линейно независимая система векторов n-мерного евклидова пространства [math](kleqslant n)[/math] . Определим по индукции понятие многомерного объема. Обозначим через [math]boldsymbol_j[/math] — перпендикуляр, опущенный из конца вектора [math]boldsymbol_j[/math] на подпространство [math]operatorname (boldsymbol_1, ldots,boldsymbol_),[/math] [math]j=2,ldots,k[/math] .

[math]V_<ast boldsymbol_1>=|boldsymbol_1|[/math] — одномерный объем — длина вектора [math]boldsymbol_1[/math] ;

Проводя ортогонализацию системы векторов [math]boldsymbol_1,boldsymbol_2, ldots, boldsymbol_k[/math] , получаем, согласно пункту 4 замечаний 8.14, перпендикуляры [math]boldsymbol_1= boldsymbol_1,boldsymbol_2, ldots,boldsymbol_k[/math] . Тогда по свойству 2 определителя Грама имеем

т.е. определитель Грама векторов [math]boldsymbol_1, boldsymbol_2, ldots, boldsymbol_k[/math] равен квадрату k-мерного объема параллелепипеда, построенного на этих векторах. В этом заключается геометрический смысл определителя Грама.

Расстоянием от конца вектора [math]boldsymbol[/math] до подпространства [math]L[/math] называется наименьшее значение длин векторов [math](boldsymbol-boldsymbol)[/math] , где [math]boldsymbolin L[/math] , т.е.

Аналогично определяется расстояние от конца вектора до многообразия.

Углом между ненулевым вектором [math]boldsymbol[/math] и подпространством [math]L[/math] называется наименьший угол [math]varphi[/math] между вектором [math]boldsymbol[/math] и ненулевыми векторами подпространства, т.е.

Аналогично определяется угол между вектором и многообразием, как угол между вектором и однородной частью многообразия.

Из неравенств пункта 1 замечаний 8.14 следует, что

1) расстояние [math]d[/math] от конца вектора [math]boldsymbol[/math] до подпространства [math]L[/math] равно длине перпендикуляра [math]boldsymbol[/math] , опущенного из конца вектора [math]boldsymbol[/math] на подпространство [math]L[/math] , т.е. [math]d=|boldsymbol|[/math] ;

2) угол между ненулевым вектором [math]boldsymbol[/math] и подпространством [math]L[/math] равен углу между вектором [math]boldsymbol[/math] и его ортогональной проекцией на подпространство [math]L[/math] .

Для нахождения расстояний и углов можно использовать формулу (8.37).

Пусть задан вектор [math]boldsymbol[/math] и подпространство [math]L=operatorname (boldsymbol_1,ldots,boldsymbol_r)[/math] , причем векторы [math]boldsymbol_1, ldots, boldsymbol_r[/math] линейно независимы. Тогда [math]V_<ast boldsymbol_1,ldots, boldsymbol_r, boldsymbol>= V_<ast boldsymbol_1,ldots,boldsymbol_r>cdot |boldsymbol|[/math] , где [math]boldsymbol[/math] — ортогональная составляющая вектора [math]boldsymbol[/math] относительно подпространства [math]L[/math] . Отсюда, [math]boldsymbol= frac<V_<ast boldsymbol_1,ldots, boldsymbol_r, boldsymbol>><V_<ast boldsymbol_1,ldots,boldsymbol_r>>[/math] . Используя (8.37) для вычисления объемов, получаем, что длина [math]|boldsymbol|[/math] ортогональной составляющей (расстояние от конца вектора [math]boldsymbol[/math] до подпространства [math]L=operatorname( boldsymbol_1,ldots,boldsymbol_r)[/math] находится по формуле

а угол [math]varphi[/math] между ненулевым вектором [math]boldsymbol[/math] и подпространством находится по формуле

Пример 8.22. В пространстве [math]mathbb^4[/math] со стандартным скалярным произведением (8.27) заданы: вектор [math]v=begin-3&2&0&0end^T[/math] и подпространство [math]L[/math] — множество [math][/math] решений однородной системы:

Требуется найти расстояние [math]|h|[/math] от конца вектора [math]boldsymbol[/math] до подпространства [math]L[/math] и угол между вектором [math]boldsymbol[/math] и подпространством [math]L[/math] .

Решение. Базис подпространства был найден в примере 8.9:

Составляем определители Грама [math]Bigl(langle boldsymbol, boldsymbol_1rangle= (-3)^2+ 2^2+0^2+0^2=13Bigr)[/math] , остальные скалярные произведения векторов найдены в примере 8.20):

Тогда [math]|h|=sqrt<frac>=sqrt<frac>[/math] , а [math]varphi= arcsinsqrt<frac>[/math] . В найдены ортогональная проекция [math]l=begindfrac&dfrac&dfrac&dfracend^T[/math] и ортогональная составляющая [math]h=begindfrac& dfrac&dfrac& dfrac end^T[/math] . Вычисляя длину вектора [math]h[/math] , получаем [math]|h|=sqrt<frac>[/math] . Результаты совпадают.

Видео:Собственные значения и собственные векторыСкачать

33. Матрица Грама в евклидовом пространстве

Пусть Еn – N-Мерное евклидово пространство и пусть Е = (Е1, Е2, . , Еn ) – базис в нём. Так как в Еn для любой упорядоченной пары векторов определено их скалярное произведение, то определены скалярные произведения всех пар базисных векторов. Составим из них матрицу

Г = (41)

Матрица Г Называется Матрицей Грама Скалярного произведения для базиса Е.

Используя матрицу Грама, можно получить формулу для вычисления скалярного произведения векторов,

Пусть в базисе Е заданы векторы А = Х1Е1 + Х2Е2 + … + ХnЕn , В = У1Е1+ У2Е2 + … + УnЕn . Тогда (А, в) = (Х1Е1 + Х2Е2 + … + ХnЕn)×( у1Е1+ У2Е2 + … + УnЕn) = = Х Т×Г×У, где Х Т– строка координат вектора А, У – Столбец координат вектора В . Итак, (А, в) = Х Т×Г×У (42).

Свойства матрицы Грама.

10. Матрица Грама симметрична относительно главной диагонали.

20. Диагональные элементы матрицы Грама строго положительны.

Это следует из того, что Ек ¹ 0 и, следовательно, (Ек, ек ) > 0.

30. Для матрицы Грама и любого N-Мерного столбца Х Выполняется условие Х Т×Г×Х > 0.

Это следует из 4-ой аксиомы определения скалярного произведения.

Симметрическую матрицу А, Удовлетворяющую условию Х Т×А×Х > 0 для любого

Ненулевого столбца Х, Называют Положительно определённой. Следовательно, матрица

Грама Положительно определённая.

Формула (42) даёт связь матриц Грама в разных базисах.

50. Определители матриц Грама во всех базисах имеют один и тот же знак.

Из формулы (43) следует ú Г1ú =ú ТТú ×úГú ×úТú = úГú ×úТú 2. Так как |Тú 2> 0, то ú Г1ú и ú Гú имеют одинаковые знаки.

60. Все главные миноры матрицы Грама строго положительны.

1. Во множестве М2 Квадратных матриц с действительными элементами скалярное произведение задано формулой . Найти матрицу Грама этого произведения в базисе Е1 = , Е2 = , Е3 = , Е4 = .