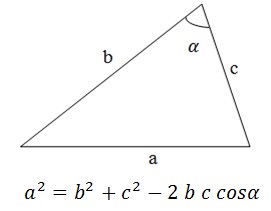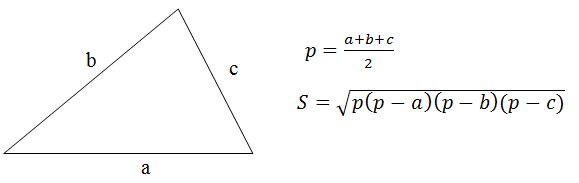1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Содержание Видео:Вычисляем высоту через координаты вершин 1Скачать  Как найти координаты вершин треугольника через векторДаны координаты середин сторон треугольника: E(7, 8); F(-4, 5); K(1, -4). Определить координаты вершин треугольника. пусть точки A, B и C — вершины треугольника, точка E — середина стороны AB, точка F — середина стороны AC, а K — середина стороны BC. Требуется найти координаты точек A, B и C.
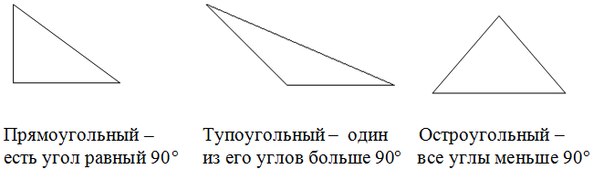
Подставляя в эти формулы координаты точек E, F и K, мы для определения неизвестных получим следующие уравнения: а) Уравнения, отмеченные (1), после подстановки в них координат точки E запишутся так: Видео:Вычисляем угол через координаты вершинСкачать  Вычислительная геометрия, или как я стал заниматься олимпиадным программированием.Часть 1Здравствуйте, уважаемые хабравчане! Это моя вторая статья, и мне хотелось бы поговорить о вычислительной геометрии. Немного историиЯ являюсь студентом уже 4 курса математического факультета, и до того как я начал заниматься программированием, я считал себя математиком на 100 процентов. В конце первого курса мой преподаватель по информатике, который занимается олимпиадным программированием, обратил на меня внимание. Им как раз не хватало одного математика в команду. Так потихоньку меня начали приучать к олимпиадному программированию. Скажу честно, для меня это было очень сложно: для человека, который узнал слово Delphi на первом курсе. Однако мой преподаватель оказался очень грамотным специалистом и нашел хороший подход ко мне. Он начал давать мне математические задачи, который я сначала решал чисто математически, а уже потом писал код (с грехом пополам). Мне очень нравится подход моего преподавателя: «разберись с этой темой, а потом расскажи нам, да так чтоб мы все поняли». Итак, первой на самом деле важной задачей, с которой мне поручили разобраться, было именно вычислительная геометрия, необходимо было разобраться в типичных задач этого раздела информатики. И я решил подойти к этой задаче со всей ответственностью. Я помню, как долго мучился с этими задачами, чтобы они прошли все тесты на сайте informatics.mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии. Вступление«Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач. Такие задачи возникают в компьютерной графике, проектировании интегральных схем, технических устройств и др. Исходными данными в такого рода задачах могут быть множество точек, набор отрезков, многоугольники и т.п. Результатом может быть либо ответ на какой-то вопрос, либо какой-то геометрический объект». Поскольку статья является достаточно большой я решил разбить ее на две части: первая часть посвящена многоугольникам, вторая – взаимному расположению различных геометрических объектов. Немного теории о векторахОтрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления. Длиной ненулевого вектора AB называется длина отрезка AB. Длина нулевого вектора считается равной нулю. Скалярное произведение векторовСкалярное произведение векторов — это число, равное произведению длин этих векторов на косинус угла между ними. Косое произведение векторовПсевдоскалярным или косым произведением векторов на плоскости называется число Косое произведение векторов в задачах вычислительной геометрии занимает такое же почетное место, как рекурсии в комбинаторике. Это своего рода жемчужина вычислительной геометрии. Практически каждая задача вычислительной геометрии имеет более простое решение с помощью косового произведение вместо лобового решения. А теперь займемся практикойНачнем с треугольников Задача №1Задача очень простая, а именно: по введенным трем числам a, b, c определить существует ли треугольник с такими сторонами. Решение Задача №2Задача является очень похожей на предыдущую с той разницей, что треугольник задан не сторонами, а координатами вершин. Решение Во всех следующих задачах будем считать, что треугольник существует, поскольку процедуру проверки существования треугольника мы только что рассмотрели. Задача №3Треугольник задан своими сторонами. Определить тип треугольника: тупоугольный, прямоугольный или остроугольный. Решение Из курса геометрии известно, что напротив большей стороны лежит больший угол (он нам и нужен). Поэтому если мы выясним чему равен больший угол, то поймем тип треугольника:
Воспользуемся теоремой косинусов: Очевидно, что если косинус угла больше нуля то угол меньше 90°, если он равен нулю, то угол равен 90°, если он меньше нуля, то угол больше 90°. Однако немного поразмыслив можно понять, что вычислять косинус угла не обязательно, необходимо учесть лишь его знак:
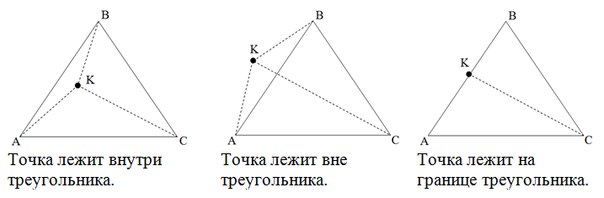
где a – большая сторона. Задача №4Задача аналогична предыдущей задаче, только треугольник задан не своими сторонами, а координатами вершин. Решение Задача №5По данным сторонам треугольника найти его площадь. Решение Задача №6Вычислить площадь треугольника заданного координатами своих вершин. Решение Задача №7Дана точка и треугольник заданный координатами своих вершин. Определить лежит ли точка внутри, на границе или вне этого треугольника. Решение Метод площадей
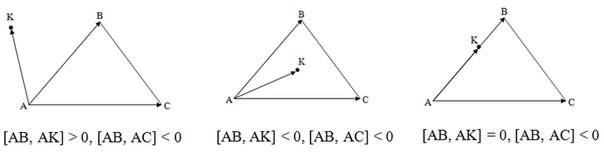
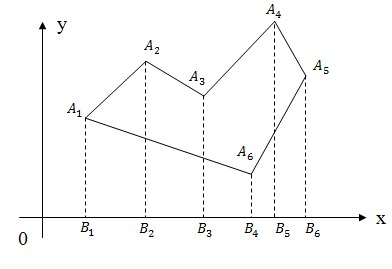
Проверка полуплоскостейЕсли хотя бы одна из сторон треугольника «разводит» противолежащую ей вершину и точку по разным полуплоскостям, то точка лежит вне треугольника. Иначе, если точка принадлежит хотя бы одной из прямых, содержащих стороны треугольника, то она находится на границе треугольника. Иначе точка лежит внутри треугольника. Задача №8Вычисление площади многоугольника заданного координатами своих вершин. Решение Данную задачу можно решить двумя способами: вычисляя ориентированные площади трапеций и треугольников. Метод трапеций
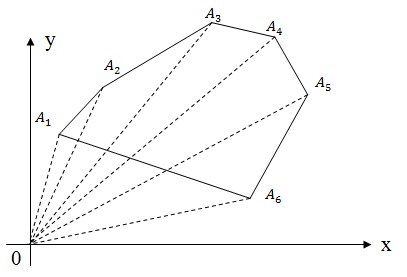
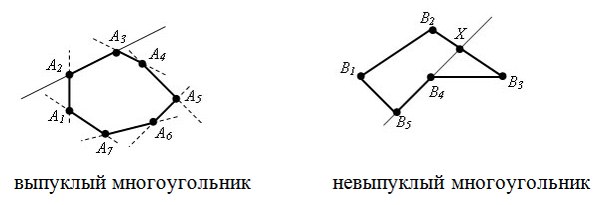
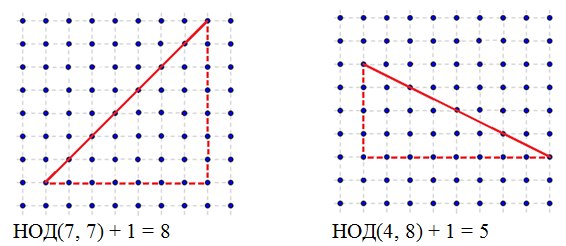
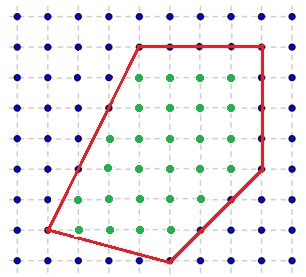
Поскольку полученная площадь является ориентированной, необходимо вычислить ее модуль. Метод треугольниковКак вы видите задача вычисления площади многоугольника достаточна проста. Не знаю, почему, но мне больше нравится решать эту задачу методом разбиения на трапеции (наверно потому, что на всех олимпиадах я ее так решал). Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть. Задача №9Многоугольник задан координатами своих вершин в порядке его обхода. Необходимо проверить является ли многоугольник выпуклым. Решение Задача опять сводится к вычислению косового произведения векторов, а именно у выпуклого многоугольника знаки косых произведений [Ai Ai+1, Ai+1 Ai+2] либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки. Задача №10Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе). Решение Для любого многоугольника с целочисленными координатами вершин справедлива формула Пика: S = n + m/2 — 1, где S – площадь многоугольника, n – количество целых точек лежащих строго внутри многоугольника, m – количество целых точек лежащих на границе многоугольника. Поскольку площадь многоугольника мы знаем как вычислять, то S известно. Так же мы можем вычислить количество целых точек лежащих на границе многоугольника, поэтому в формуле Пика остается лишь одна искомая неизвестная которую мы можем найти. Вот и все! Надеюсь, Вам понравилась статья, и я напишу ее вторую часть. 📸 ВидеоМетод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать  Нахождение координат вектора. Практическая часть. 9 класс.Скачать  Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать  Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать  Уравнения стороны треугольника и медианыСкачать  Координаты вектора. 9 класс.Скачать  №933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать  Математика без Ху!ни. Смешанное произведение векторовСкачать  Координаты точки и координаты вектора 1.Скачать  Вычисление медианы, высоты и угла по координатам вершинСкачать  Угол между векторами | МатематикаСкачать  Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать  Высшая математика. 3 урок. Аналитическая геометрия. Вычисление площади треугольникаСкачать  №973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  №942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать  №1049. Найдите углы треугольника с вершинами А (-1; √3), В(1;-√3 )Скачать  Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать  Векторы. Метод координат. Вебинар | МатематикаСкачать  | ||

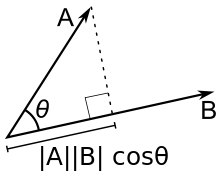
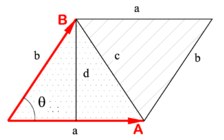
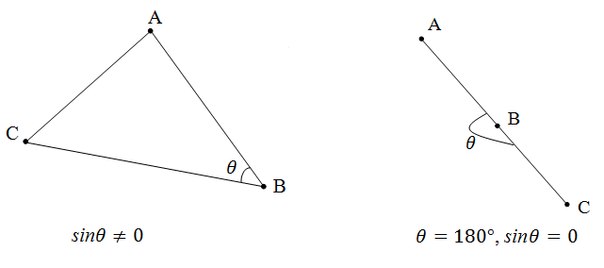
 — угол вращения (против часовой стрелки) от a к b. Если хотя бы один из векторов a и b нулевой, то полагают [a, b] = 0.
— угол вращения (против часовой стрелки) от a к b. Если хотя бы один из векторов a и b нулевой, то полагают [a, b] = 0.