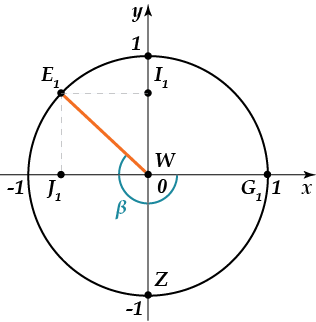Как найти координаты точки единичной окружности полученной поворотом точки (8 видео)

Тригонометрия

Найти координаты точки на единичной окружности, полученной поворотом точки ( Aleft( 1;0 right) ) на ( -225^circ ) .

Окружность единичная с центром в точке ( left( 0;0 right) ) , значит, мы можем воспользоваться упрощёнными формулами:

( beginx=cos beta =cos (-225^circ )\y=sin beta =sin (-225^circ )end ) .

Можно заметить, что ( -225^circ =-360^circ +135^circ ; -225^circ =-180^circ -45^circ ) . Изобразим рассматриваемый пример на рисунке:

Радиус ( <_>W ) образует с осью ( x ) углы, равные ( 45^circ ) и ( 135^circ ) . Зная, что табличные значения косинуса и синуса ( 45^circ ) равны ( displaystyle dfrac<sqrt> ) , и определив, что косинус здесь принимает отрицательное значение, а синус положительное, имеем:

Подробней подобные примеры разбираются при изучении формул приведения тригонометрических функций в теме «Формулы тригонометрии».

Таким образом, искомая точка имеет координаты ( left( -dfrac<sqrt>;dfrac<sqrt> right) ) .

Видео:Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать

10.V-3. Поворот точки вокруг начала координат-2

Алгебра. 10 класс. Тригонометрия. Тест 3.

Вариант 1.

1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 3π/2±π.

A) (0; -1); B) (0; 1); C) (1; 0); D) (-1; 0).

2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π/6±π.

3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π+πk, где kϵZ.

A) (-1; 0); (1; 0); B) (0; -1); (1; 0); C) (1; 0); (0; 1); D) (0; -1); (-1; 0).

4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить

A) 3π/4+2πk, kϵZ; B) -π/4+2πk, kϵZ; C) π/4+2πk, kϵZ; D) 7π/4+2πk, kϵZ.

5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались

A) π/6+πk, kϵZ; B) π/3+2πk, kϵZ; C) -π/3+πk, kϵZ; D) -π/6+2πk, kϵZ.

6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=π/2+πk, kϵZ. Записать те из них, которые принадлежат отрезку [-5π; -7π/2].

A) -9π/2; -4π; B) -9π/2; -7π/2; C) -7π/2; D) -5π; -9π/2.

7. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±5π/6+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [3π; 9π/2].

A) 19π/6; B) 17π/6; C) 4π; D) 13π/6.

8. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±π/3+πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-2π; -π/2].

A) -5π/3; -4π/3; B) -4π/3; -2π/3; C) -5π/3; -4π/3; -2π/3; D) -2π; -4π/3; -2π/3.

Вариант 2.

1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π/2±π.

A) (0; -1); B) (0; 1); C) (1; 0); D) (-1; 0).

2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π/3±π.

3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -π+πk, где kϵZ.

A) (-1; 0); (0; -1); B) (0; -1); (1; 0); C) (1; 0); (0; 1); D) (1; 0); (-1; 0).

4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить

A) 5π/6+2πk, kϵZ; B) π/6+2πk, kϵZ; C) -π/6+2πk, kϵZ; D) 5π/3+2πk, kϵZ.

5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались

A) -π/4+πk, kϵZ; B) π/4+πk, kϵZ; C) -π/8+πk, kϵZ; D) -π/6+2πk, kϵZ.

6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=πk, kϵZ. Записать те из них, которые принадлежат отрезку [4π; 11π/2].

A) 9π/2; 5π; B) 4π; 9π/2; C) 4π; 5π; D) 5π.

7. Точке М единичной окружности соответствует бесконечное множество действительных чисел -π/4+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-9π/2; -3π].

A) -13π/4; B) -19π/4; C) -15π/4; D) -17π/4.

8. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±2π/3+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-5π; -7π/2].

A) -16π/3; B) -14π/3; C) -13π/3; D) -3π; -14π/3.

Вариант 3.

1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -π/2±π.

A) (0; 1); B) (0; -1); C) (1; 0); D) (-1; 0).

2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 3π/4±π.

3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -3π/2+πk, где kϵZ.

A) (-1; 0); (0; -1); B) (0; 1); (0; -1); C) (1; 0); (0; 1); D) (1; 0); (-1; 0).

4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить

A) 5π/3+2πk, kϵZ; B) π/3+2πk, kϵZ; C) π/6+2πk, kϵZ; D) 7π/6+2πk, kϵZ.

5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались

A) -π/6+πk, kϵZ; B) -π/4+πk, kϵZ; C) -π/3+πk, kϵZ; D) π/6+2πk, kϵZ.

6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=5π/6+2πk, kϵZ. Записать те из них, которые принадлежат отрезку [-6π; -4π].

A) -5π; B) -29π/6; C) -25π/6; D) -31π/6.

7. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±π/4+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-5π; -3π].

A) -17π/4; B) -15π/4; C) -15π/4; -17π/4; D) -13π/4; -15π/4.

8. Точке М единичной окружности соответствует бесконечное множество действительных чисел π/4+πk/2, где kϵZ. Записать те из них, которые принадлежат отрезку [5π; 13π/2].

A) 21π/4; 23π/4; 25π/4; B) 21π/4; 23π/4; C) 23π/4; 25π/4; D) 23π/4.

Вариант 4.

1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -3π/2±π.

A) (-1; 0); B) (0; 1); C) (1; 0); D) (0; -1).

2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 5π/6±π.

3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 3π/2+πk, где kϵZ.

A) (-1; 0); (0; -1); B) (0; -1); (0; 1); C) (1; 0); (0; 1); D) (1; 0); (-1; 0).

4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить

A) π/3+2πk, kϵZ; B) -π/3+2πk, kϵZ; C) 2π/3+2πk, kϵZ; D) π/6+2πk, kϵZ.

5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались

A) π/6+πk, kϵZ; B) -π/4+πk, kϵZ; C) π/3+πk, kϵZ; D) π/4+πk, kϵZ.

6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=π/3+2πk, kϵZ. Записать те из них, которые принадлежат отрезку [-5π/2; -π].

A) -5π/3; B) -π/3; -4π/3; C) -2π/3; D) -4π/3.

7. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±π/3+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-2π; -π/2].

A) -π/3; B) -2π/3; C) -4π/3; D) -5π/3.

8. Точке М единичной окружности соответствует бесконечное множество действительных чисел π/4+πk/2, где kϵZ. Записать те из них, которые принадлежат отрезку [-7π/2; -5π/2].

A) -13π/4; B) -13π/4; -11π/4; C) -11π/4; D) -3π.

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Поворот точки вокруг начала координат

Рассмотрим на координатной плоскости окружность радиуса 1 с центром в начале координат. Ее называют единичной окружностью. Введем понятие поворота точки единичной окружности во круг начала координат на угол α радиан, где α – любое действительное число.

1. 1. Пусть α>0. Предположим, что точка, двигаясь поединичной окружности от точки Р против часовой стрелки, прошла путь длиной α (рис. 1). Конечную точку пути обозначим М.

В этом случае будем говорить, что точка М получена из точки Р поворотом вокруг начала координат на угол α радиан.

Частные случаи решения уравнений tg x = a

Уравнение	Решение

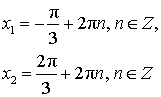tg x = – 1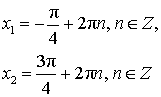

tg x = 0

tg x = 1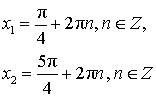

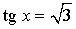20(1). Вопрос: Определение производной, правила дифференцирования, примеры.

Ответ: Производная функции − одно из основных понятий математики, а в математическом анализе производная наряду с интегралом занимает центральное место. Процесс нахождения производной называется дифференцированием. Обратная операция − восстановление функции по известной производной − называется интегрированием.

Производная функции в некоторой точке характеризует скорость изменения функции в этой точке.

1. Вопрос: Аксиомы стереометрии. Следствия из аксиом (доказать одно из них).

Ответ: А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

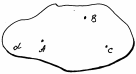Как найти координаты точки единичной окружности полученной поворотом точки

(точки А, В, С лежат в плоскости

) С

А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

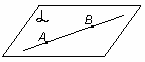АB

Прямая АВ лежит в плоскости

Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.

= М Прямая а и плоскость

пересекаются в точке М.

А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

= a

пересекаются по прямой а.

Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

1) Рассмотрим прямую a и точку A, которая не находится на этой прямой.

2) На прямой a выберем точки B и C.

3) Так как все 3 точки не находятся на одной прямой, из второй аксиомы следует, что через точки A, B, Cи можно провести одну единственную плоскостьα.

4) Точки прямой a, B и C, лежат на плоскостиα, поэтому из третьей аксиомы следует, что плоскость проходит через прямую a и, конечно, через точку A.

Следствие 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

2. Вопрос: Теорема о параллельности трех прямых (формулировка и доказательство).

Ответ: Две прямые, параллельные третьей прямой, параллельны.

Выберем точку M на прямой b.

Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).

Возможны два случая:

1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.

Пусть прямая b пересекает плоскость α.

Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным.

Значит, прямая b находится в плоскости α.

Теперь нужно доказать, что прямые a и b параллельны.

Пусть у прямых a и b есть общая точка L.

Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по теореме (Через любую точку пространства вне данной прямой можно провести прямую, параллельную данной прямой, и при том только одну.) это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.

Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.

3. Вопрос: Параллельные прямые в пространстве(определение). Теорема о параллельных прямых.

Ответ: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Теорема о параллельных прямых: Через любую точку пространства, не лежащую на данной прямой проходит прямая, параллельная данной, и притом только одна.

4. Вопрос: Параллельность прямой и плоскости(определение). Признак параллельности прямой и плоскости.

Ответ: Прямая и плоскость называются параллельными, если они не имеют общих точек.

Признак параллельности прямой и плоскости:Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то прямая параллельна самой плоскости.

5. Вопрос: Расположение прямых в пространстве(виды). Признак скрещивающихся прямых.

Ответ:

Признак скрещивающихся прямых: Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.

6. Вопрос: Углы с сонаправленными сторонами. Определение, теорема.

7. Вопрос: Признак параллельности двух плоскостей.

Ответ: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то плоскости параллельны.

8. Вопрос: Свойства параллельности плоскостей(доказать одно из них)

Ответ: Всего 3 свойства.

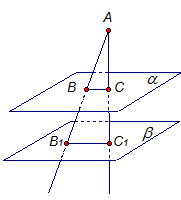
С1:Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

Пусть даны параллельные плоскости и и плоскость , которая пересекает плоскости и по прямым а и b соответственно (Рис. 1.).

Прямые а и b лежат в одной плоскости, а именно в плоскости γ. Докажем, что прямые а и b не пересекаются.

Если бы прямые а и b пересекались, то есть имели бы общую точку, то эта общая точка принадлежала бы двум плоскостям и , и , что невозможно, так как они параллельны по условию.

Итак, прямые а и b параллельны, что и требовалось доказать.

С2: Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

Пусть даны параллельные плоскости и и параллельные прямые АВ и СD, которые пересекают эти плоскости (Рис. 2.). Докажем, что отрезки АВ и СD равны.

Две параллельные прямые АВ и СD образуют единственную плоскость γ, γ = АВDС. Плоскость γ пересекает параллельные плоскости и по параллельным прямым (по первому свойству). Значит, прямые АС и ВD параллельны.

Прямые АВ и СD также параллельны (по условию). Значит, четырехугольник АВDС – параллелограмм, так как его противоположные стороны попарно параллельны.

Из свойств параллелограмма следует, что отрезки АВ и СD равны, что и требовалось доказать.

С3: Параллельные плоскости рассекают стороны угла на пропорциональные части.

Пусть нам даны параллельные плоскости и , которые рассекают стороны угла А (Рис. 3.). Нужно доказать, что .

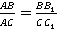
Параллельные плоскости и рассечены плоскостью угла А. Назовем линию пересечения плоскости угла А и плоскости – ВС, а линию пересечения плоскости угла А и плоскости – В₁С₁. По первому свойству, линии пересечения ВС и В₁С₁ параллельны.

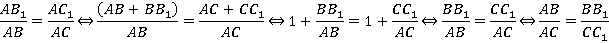
9. Вопрос: Тетраэдр и параллелепипед. Определения. Свойства параллелепипеда.

Ответ: Тетраэдр — поверхность, составленная из четырёх треугольников DАВ, DВС, DАС и АВС.

АВС,

DАС,

DВС,

DАВ — грани. отрезки DА, DВ, АВ и т.д. — рёбра. точки А, В, С и т.д. — вершины. Рёбра АD и ВС — противоположные. Считается

АВС — основание, остальные грани — боковые.

Параллелепипед. АВСDA₁B₁C₁D₁: поверхность, составленная из двух равных параллелограммов АВСD и A₁B₁C₁D₁, лежащих в параллельных плоскостях и четырёх параллелограммов.

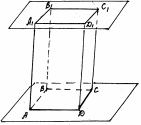	все параллелограммы — грани, их стороны — рёбра, их вершины — вершины параллелепипеда. Считается: АВСD и A₁B₁C₁D₁ — основания, остальные грани — боковые.
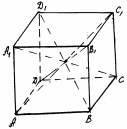рис. 29	Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда: A₁C, D₁B, AC₁, DB₁.

Свойства:
1. Противоположные грани параллелепипеда параллельны и равны.

Для любой пары противолежащих граней параллелепипеда имеем: соответствующие углы равны (например, , и т. д.); соответствующие стороны равны и параллельны ( и , и и т. д. как противолежащие стороны параллелограммов). Отсюда и их плоскости параллельны.
2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

10. Вопрос: Признак перпендикулярности прямой и плоскости.

Ответ:Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.

11. Вопрос: Теорема о трёх перпендикулярах.

Ответ: Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

12. Вопрос: Признак перпендикулярности двух плоскостей.

Ответ: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

13. Вопрос: Призма. Основные элементы, S_бок, S_полн, V_призмы.

Ответ: Призма — это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани — параллелограммами.

14. Вопрос: Пирамида. Основные элементы, S_бок, S_полн, V_{пирамиды}.

Ответ: Пирамида – многогранник, одна из граней которого (называется основанием) – произвольный многоугольник, а остальные грани соединяются в одной точке(вершине).

15. Вопрос: Усечённаяпирамида. Основные элементы, S_бок, S_полн.

Ответ: Усечённой пирамидой называется часть пирамиды, заключенная между её основанием и сечением пирамиды, параллельным основанию.

16. Вопрос: Двугранный угол. Градусная мера двугранного угла.

Ответ: Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой.Двугранный угол измеряется величиной своего линейного угла.Чтобы найти величину двугранного угла или угла между плоскостями, нужно построить линейный угол и найти величину этого линейного угла.

17. Вопрос: Прямоугольный параллелепипед. Свойства прямоугольного параллелепипеда (доказать одно из них).

Ответ: Прямоугольный параллелепипед — многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником. Противолежащие грани параллелепипеда равны.

Свойства прямоугольного параллелепипеда:

С1:В прямоугольном параллелепипеде все шесть граней прямоугольники.

С2: Боковые ребра перпендикулярны основанию. Значит, все боковые грани прямоугольного параллелепипеда — прямоугольники.

С3: Все двугранные углы прямоугольного параллелепипеда прямые.

Рассмотрим, например, двугранный угол прямоугольного параллелепипеда с ребром АВ, т. е. двугранный угол между плоскостями АВВ1 и АВС.

АВ – ребро, точка А1 лежит в одной плоскости – в плоскости АВВ1, а точка D в другой – в плоскости А1В1С1D1. Тогда рассматриваемый двугранный угол можно еще обозначить следующим образом: ∠А1АВD.

Возьмем точку А на ребре АВ. АА1 – перпендикуляр к ребру АВ в плоскости АВВ1, AD перпендикуляр к ребру АВ в плоскости АВС. Значит, ∠А1АD –линейныйуголданногодвугранногоугла. ∠А1АD = 90°, значит, двугранныйуголприребреАВравен 90°.

∠(АВВ1, АВС) = ∠(АВ) = ∠А1АВD= ∠А1АD = 90°.

Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые.

18. Вопрос: Понятие многогранника. Виды. Примеры.

Ответ: Если поверхности геометрических тел составлены из многоугольников, то такие тела называются многогранниками.

19. Вопрос: Правильная пирамида. Определение, S_бок.

Ответ: Пирамида называется правильной, если её основанием является правильный многоугольник, при этом вершина такой пирамиды проецируется в центр ее основания.

20. Вопрос: Симметрия в пространстве. Правильные многогранники.

Ответ: Точки А и A₁ называются симметричными относительно точки О (центра симметрии), если О – середина отрезка AA₁. Точка О симметрична сама себе.

Точки А и A₁ называются симметричными относительно прямой а (ось симметрии) если прямая а проходит через середину отрезка AA₁ и перпендикулярна ему. Каждая точка прямой a симметрична сама себе.

Точки А и A₁ называются симметричными относительно плоскости a (плоскость симметрии) если плоскость a проходит через середину отрезка AA₁ и перпендикулярна ему. Каждая точка плоскости a симметрична сама себе.

21. Вопрос: Уравнение сферы. Взаимное расположение сферы и плоскости.

Взаимное расположение сферы и плоскости:

1. Плоскость не пересекает сферу;

2. Плоскость касается сферы;

3. Плоскость пересекает сферу.

22. Вопрос: Касательная плоскость к сфере. Свойство с доказательством.

Ответ: Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Свойство: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

Доказательство: Из условия свойства следует, что данный радиус является перпендикуляром, проведенным из центра сферы к данной плоскости. Поэтому расстояние от центра сферы до плоскости равно радиусу сферы, и, следовательно, сфера и плоскость имеют только одну общую точку. Это и означает, что данная плоскость является касательной к сфере.
23. Вопрос: Цилиндр. Основные элементы, S_бок, S_полн, V_{цилиндра}.

Ответ: Цилиндр – тело, которое состоит из двух кругов, лежащих в параллельных плоскостях и всех отрезков, соединяющих соответствующие линии этих кругов.

S_бок=2πrh, r– радиус, h– высота;

24. Вопрос: Конус. Основные элементы, S_бок, S_полн, V_конуса.

Ответ: Конусом называется тело, которое состоит из круга, точки и всех отрезков, соединяющих эту точку с точкой круга. Круг называется основанием, а отрезки — образующими. Точка называется вершиной, а высота конуса перпендикуляр, проведённый из вершины конуса к основанию.

25. Вопрос:Шар и сфера, основные элементы, S_сферы, V_шара.

Ответ: Сфера – геометрическое место точек в пространстве, равноудалённых от некоторой заданной точки (центра сферы). Расстояние между любой точкой сферы и её центром называется радиусом. Геометрическое тело, ограниченное сферой, называется шаром.