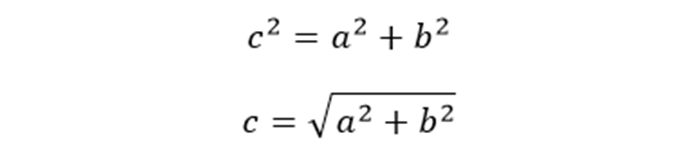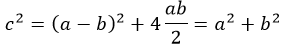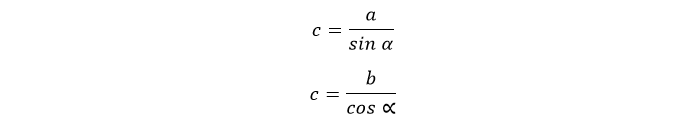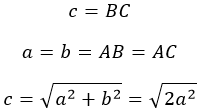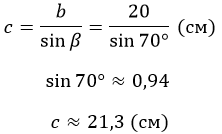Как найти гипотенузу равностороннего треугольника

Видео:Найдите гипотенузу равнобедренного прямоугольного треугольника, площадь которого равна 1Скачать

Калькулятор нахождения стороны прямоугольного треугольника

Треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.

Катет — это прилежащая прямому углу сторона треугольника.

Гипотенуза — это сторона треугольника противолежащая прямому углу. Гипотенуза является самой длинной стороной треугольника.

Видео:Теорема Пифагора для чайников)))Скачать

Теорема Пифагора

Квадрат гипотенузы равен сумме квадратов катетов

Видео:Катеты и гипотенузаСкачать

Гипотенуза — формула, правила и примеры вычислений

Слово «гипотенуза» со школьных времен у многих вызывает негативные ассоциации. Добавим загадочного и непонятного. Происходит от греческого «ὑποτείνουσα».

А ведь означает всего-навсего «вытянутый». И речь идет о простейшей форме треугольника – прямоугольной (рис. 1).

Гипотенузой называют сторону напротив прямого угла. Самую протяженную. В данном случае – с. Остальные составляющие – катеты.

Простыми фигурами интересовались древние строители Вавилона и Египта. А особенно – землемеры. Еще бы: ведь основа любой цивилизации – распределение угодий и налоги.

Считается, что теоретическая база была доказательно предложена Пифагором в V-м веке до н. э. Хотя, скорее всего, это было сделано ранее.

Видео:Теорема о биссектрисе угла треугольника | Осторожно, спойлер! | Борис Трушин |Скачать

Теорема Пифагора

Сумма квадратов катетов составляет квадрат гипотенузы:

Верно и обратное утверждение. Треугольник, удовлетворяющий приведенному равенству – прямоугольный.

Формула верна только в Евклидовой геометрии, где параллельные прямые не пересекаются.

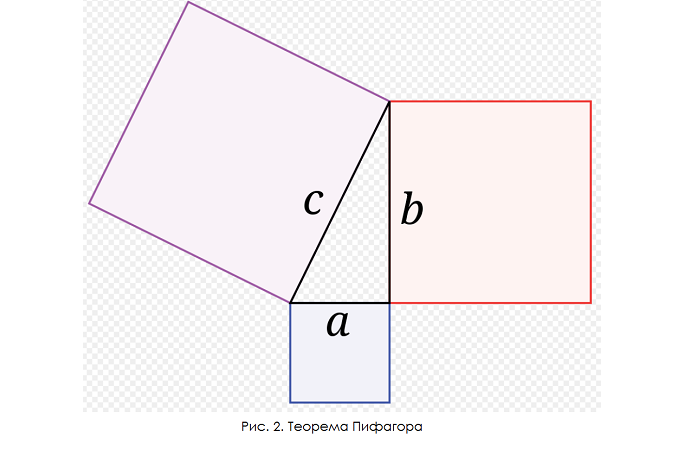
Утверждение приведено в современной интерпретации. В оригинале выглядит несколько по-другому: площадь квадрата, построенного на гипотенузе, идентична сумме площадей квадратов, построенных на катетах (рис. 2).

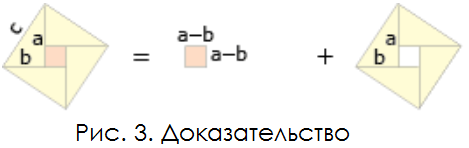
Существует масса способов доказательства. В том числе весьма сложных. А попадаются удивительно изящные, как например, на рисунке 3:

Видео:Определение длины гипотенузыСкачать

В тригонометрии

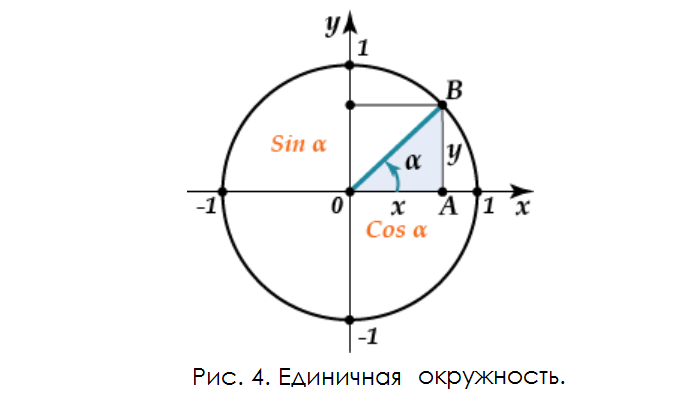
Построим на плоскости прямоугольную систему координат с единичной (с радиусом, равным 1) окружностью с центром в точке (0; 0). B – пересечение угла α и кривой (рис. 4).

На оси абсцисс X отмечается cos α; на оси ординат Y – sin α.

В получившемся прямоугольном треугольнике отрезок 0B является гипотенузой. Учитывая доказанную теорему, выводим основное равенство математической дисциплины:

sin 2 α + cos 2 α = 1

Видео:КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Гипотенуза прямоугольного треугольника

Связана со сторонами следующими соотношениями (см. рис. 1):

a – противолежащий α катет;

Величины sin α и cos α меньше либо равны 1, что очевидно из рис. 4. Но в треугольнике не может быть два прямых угла. Как не может быть нулевого.

Это означает, что гипотенуза – всегда наибольшая сторона треугольника, т. е.

Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

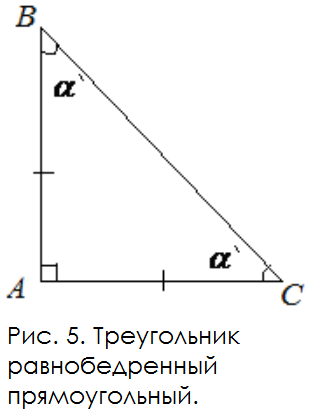
Гипотенуза равнобедренного треугольника

В такой фигуре катеты равны и являются сторонами прямого угла (рис. 5). Расчет гипотенузы c производится по формуле теоремы Пифагора.

Нетрудно заметить, что углы α = 45°. Поскольку сумма всех равна 180°.

Видео:№254. Найдите углы равнобедренного прямоугольного треугольника.Скачать

Пример решения задачи

Дан прямоугольный треугольник ABC (рис. 1). Рассчитайте длину AB, если b = 20 см, а β = 70°.

AC является катетом, противолежащим углу β. Значит нахождение гипотенузы сводится к отношениям:

Ответ: АВ = 21,3 см.

В интернете есть онлайн калькуляторы для оперативного расчета величины. Но целесообразно ими пользоваться разве что при значительном объеме вычислений. Ведь формулы довольно просты.

Связанные с упомянутыми фигурами задачи распространены в реальной жизни. Приведенные уравнения призваны помочь в решении.

Видео:Самая простая нерешённая задача — гипотеза Коллатца [Veritasium]Скачать

Расчет гипотенузы треугольника

Гипотенуза треугольника — это самая длинная сторона прямоугольного треугольника, лежащая против его прямого угла.

Формула расчета гипотенузы:

c = √(a 2 + b 2 ), где

a — катет;
b — катет;
c — гипотенуза.

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета гипотенузы прямоугольного треугольника, если известны его катеты. С помощью этой программы вы в один клик сможете рассчитать гипотенузу треугольника.

🎬 Видео

Лайфхак нахождения катета в прямоугольном треугольникеСкачать

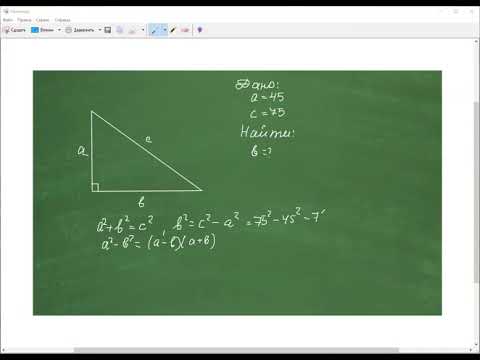
Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать

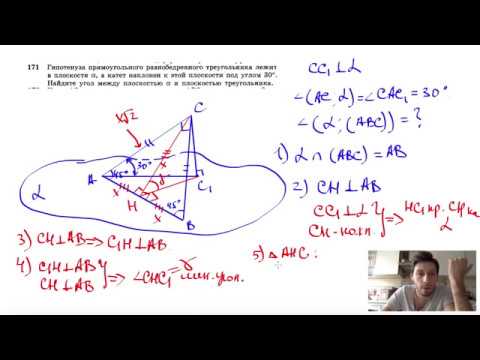
№171. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскостиСкачать

Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Нахождение стороны прямоугольного треугольникаСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Чему равна гипотенуза прямоугольного треугольника, если его периметр и площадьСкачать