- Свойства
- Усеченный конус — построение фигуры, формулы и задачи
- Исходный полный конус
- Существующие виды
- Круглая прямая фигура
- Усеченный геометрический объект
- Способы построения
- Площадь поверхности
- Формула объема
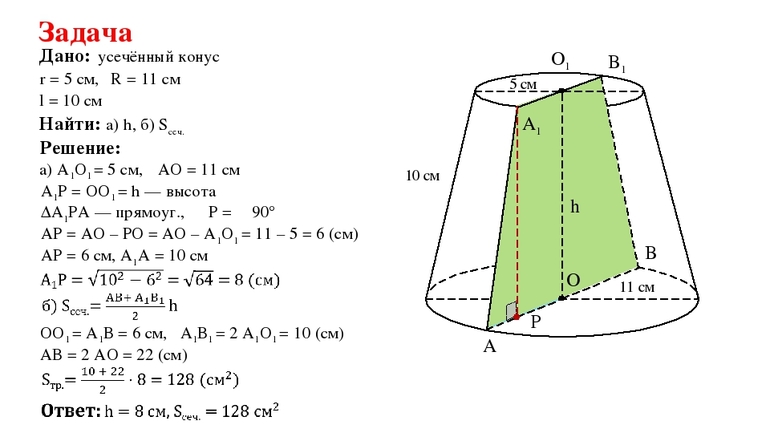
- Пример решения задачи
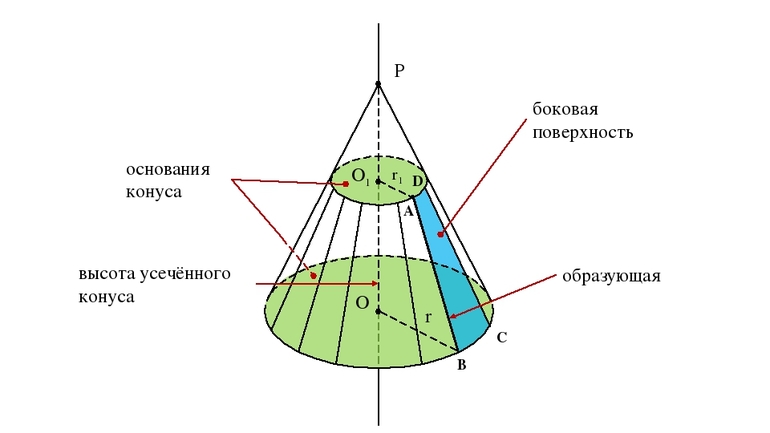
- Что такое усеченный конус: определение, основные элементы
- Определение усеченного конуса
- Основные элементы усеченного конуса
- 📸 Видео
Видео:Усеченный конус. 11 класс.Скачать

Свойства
Радиусы оснований усеченного конуса позволяют вычислить диаметры оснований, их периметр и площадь по стандартным формулам для окружности с учетом двух различных радиусов усеченного конуса. d=2r D=2R p=2πr P=2πR S_r=πr^2 S_R=πR^2
Поскольку нам известна высота усеченного конуса, но для дальнейших вычислений нужна также и образующая, то нужно построить трапецию во внутреннем пространстве усеченного конуса таким образом, чтобы она соединяла указанные величины через радиусы. В такой трапеции, поскольку она прямоугольная, можно построить дополнительный прямоугольный треугольник и найти в нем апофему по теореме Пифагора, а также углы при основаниях и апофеме, через тригонометрические отношения l=√(h^2+(R-r)^2 ) tanβ=h/(R-r) α=180°-β
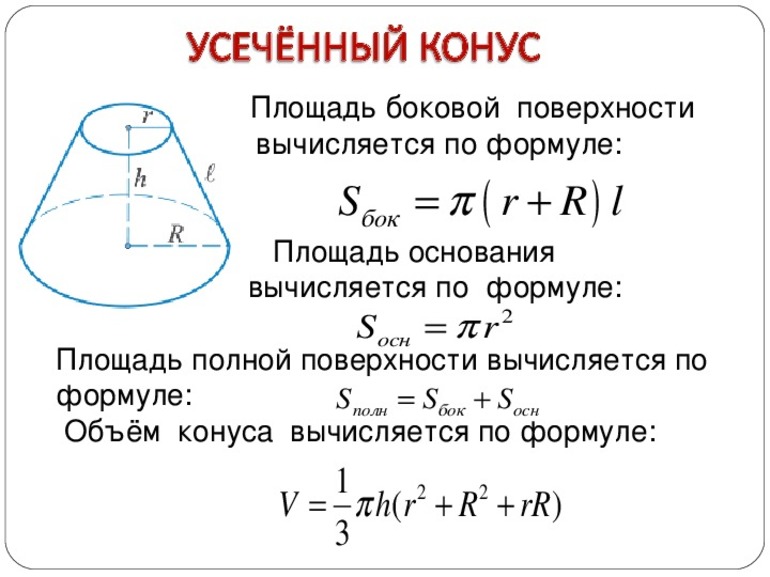
Площадь боковой поверхности усеченного конуса зависит от радиусов оснований конуса и от апофемы, которую можно найти, зная высоту, по формуле приведенной выше. Площадь полной поверхности состоит из площади боковой поверхности и площади двух оснований усеченного конуса. S_(б.п.)=πl(R+r) S_(п.п.)=S_(б.п.)+S_r+S_R=πl(R+r)+πr^2+πR^2
Найти объем усеченного конуса, зная высоту и радиусы оснований, достаточно просто, поскольку стандартная формула не предполагает других элементов расчета. V=πh/3(R^2+rR+r^2)
Видео:+Как найти длину окружностиСкачать

Усеченный конус — построение фигуры, формулы и задачи
Видео:№567. Найдите образующую усеченного конуса, если радиусы оснований равны 3 см и 6 см, а высота равнаСкачать

Исходный полный конус
Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.
Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.
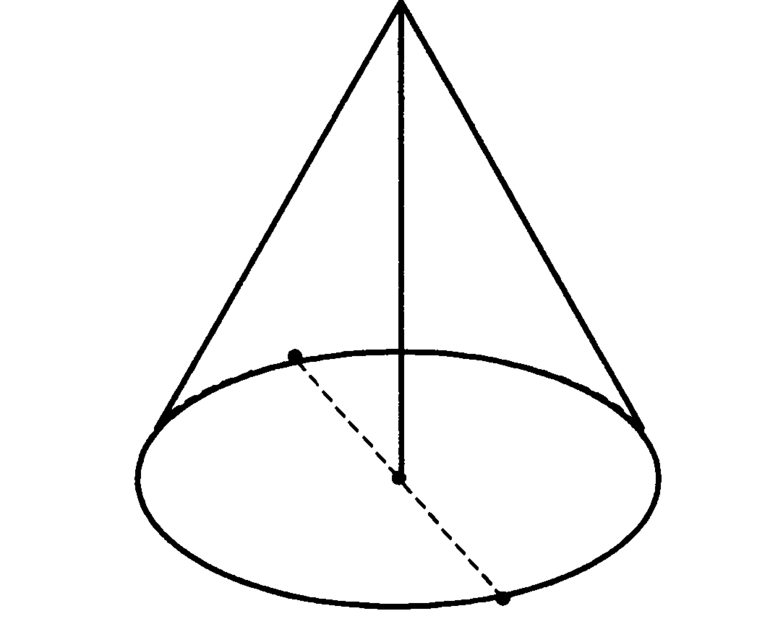
Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:
- Вершина — зафиксированная точка в пространстве, которая не лежит в плоскости замкнутой кривой.
- Коническая поверхность, образованная в результате перемещения отрезка — образующей, или генератрисы.
- Основание — часть плоскости, ограниченная исходной замкнутой кривой. Последняя является направляющей, или директрисой, для образующей.
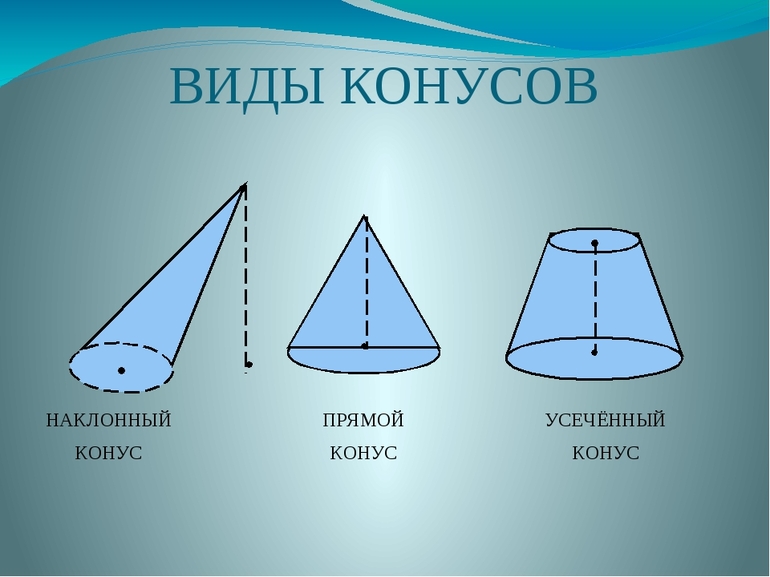
Существующие виды
В геометрии известны несколько видов конуса. Каждый из них определяется характером директрисы и расположением относительно нее генератрисы. Выделяют следующие виды фигуры:
- Круглый прямой. В его основании лежит круг, а высота (длина перпендикуляра, опущенного из вершины) соединяет центр окружности и вершину.
- Эллиптический прямой. В его основании находится эллипс, а проекция вершины попадает точно в центр основания.
- Наклонный произвольного вида. Высота в этом конусе всегда меньше, чем длина отрезка, соединяющего вершину и геометрический центр основания.
Круглая прямая фигура
Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина — высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.
С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.
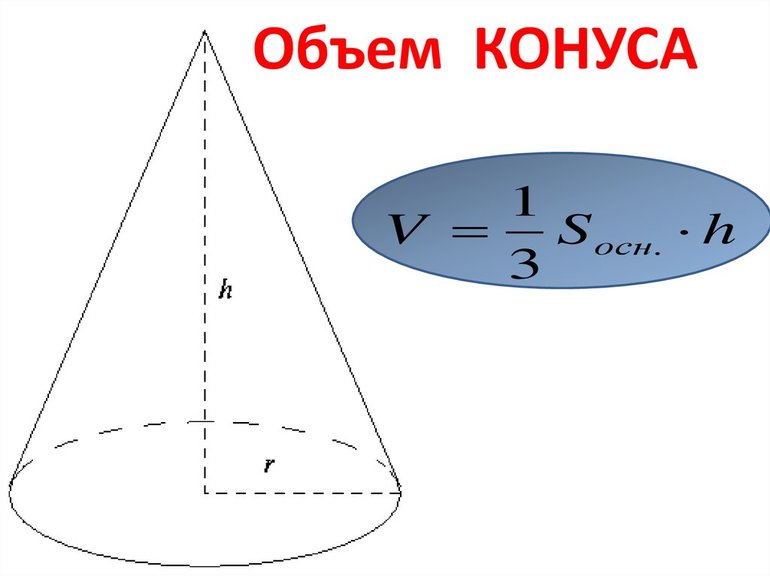
Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r 2 + pi*g*r, где число pi=3,14, r — радиус окружности в основании, g — длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.
Объем рассматриваемого конуса выражается следующей формулой: V = 1/3*pi*r 2 *h. Здесь h — высота фигуры. Можно заметить, что величина V ровно в три раза меньше аналогичной для цилиндра, имеющего то же основание, что и конус. Записанную формулу может вывести любой школьник, который знаком с интегральными вычислениями.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Усеченный геометрический объект
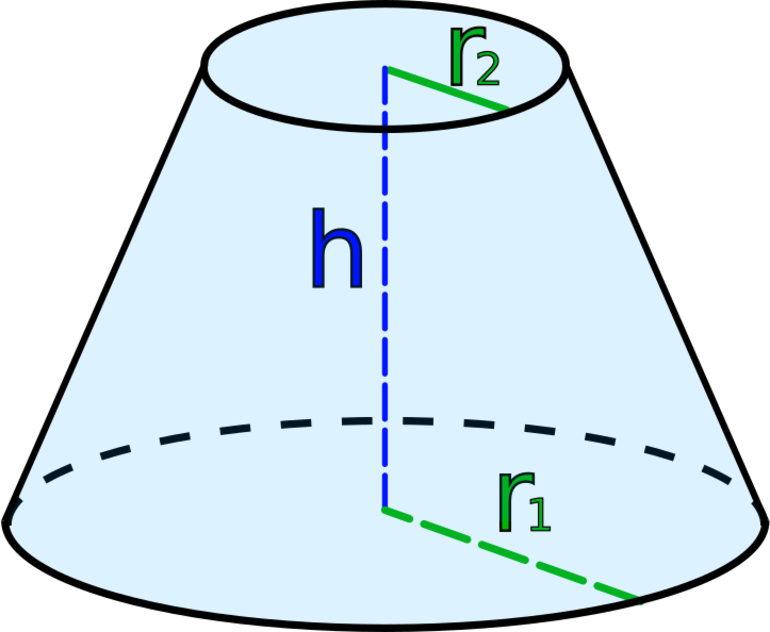
Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.
Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.
Способы построения
Можно выделить два основных способа построения усеченного круглого геометрического объекта:
- из круглого прямого конуса;
- с помощью трапеции.
В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной. Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.
Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.
Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.
Площадь поверхности
Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r 2 . Для боковой поверхности следует выполнить следующие действия:
- Разрезать ее вдоль образующей и развернуть на плоскости.
- Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
- Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
- Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую. В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).
Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:
S = S1 + S2 + Sb = pi*r1 2 + pi*r2 2 + pi*g*(r1 + r2).
Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.
Формула объема
Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:
V = 1/3*pi*r1 2 *H — 1/3*pi*r2 2 *(H-h).
Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:
V = 1/3*pi*h*(r1 2 + r2 2 + r1*r2).
Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:
V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).
Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.
Видео:11 класс, 18 урок, Усеченный конусСкачать

Пример решения задачи
Известно, что сумма площадей двух оснований усеченного прямого круглого конуса составляет 100 см 2 . При этом радиус большего основания в 2 раза превышает радиус меньшего. Необходимо найти площадь боковой поверхности фигуры, высота которой составляет 15 см.
Из данных задачи можно определить значение каждого радиуса. Для этого необходимо ввести следующее равенство: r1 = 2*r2. Тогда для суммы площадей оснований можно записать выражение:
S = S1 + S2 = pi*r1 2 + pi*r2 2 = 4*pi*r2 2 + pi*r2 2 = 5*pi*r2 2 .
Откуда получается:
r2 = (S/(5*pi))^0,5 = (100/(5*3,14))^0,5 = 2,52 см.
Тогда радиус большего основания будет равен r1 = 2*r2 = 5,04 см.
Чтобы найти генератрису g усеченного конуса, следует рассмотреть прямоугольный треугольник, который образован двумя катетами: высотой h и отрезком r1-r2. Его гипотенуза является генератрисой, она равна:
g = ((r1-r2)^2 + h 2 )^0,5 = (2,52 2 + 15 2 )^0,5 = 15,21 см.
Поскольку известны все необходимые линейные параметры усеченной фигуры, можно воспользоваться известной формулой для площади ее боковой поверхности:
Sb = pi*g*(r1 + r2) = 3,14*15,21*(2,52 + 5,04) = 361,1 см 2 .
Таким образом, усеченный конус является фигурой вращения, поверхность которой состоит из оснований и боковой части. Чтобы воспользоваться формулами для определения его площади и объема, необходимо знать любые три его линейных параметра.
Видео:Усеченный конус. Практическая часть. 11 класс.Скачать

Что такое усеченный конус: определение, основные элементы
В данной публикации мы рассмотрим определение и основные элементы усеченного конуса. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Видео:№568. Радиусы оснований усеченного конуса равны 5 см и 11 см, а образующая равна 10 см. Найдите:Скачать

Определение усеченного конуса
Усеченный конус (конический слой) – это геометрическая фигура в пространстве; часть конуса, оставшаяся между его основанием и секущей плоскостью, параллельной этому основанию.
Примечание: В рамках данной публикации мы будем рассматривать самый распространенный вид усеченного конуса – прямой круговой.
Усеченный конус образуется путем вращения на 360° прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию, или равнобедренной трапеции вокруг своей оси симметрии на 180°.
На рисунке ниже конус образован путем вращения равнобедренной трапеции ABCD вокруг оси O1O2.
Видео:Длина окружности. Математика 6 класс.Скачать

Основные элементы усеченного конуса
- R – радиус бОльшего основания конуса, являющегося кругом, с центром в точке O1 и диаметром AD.
- r – радиус меньшего основания конуса с центром в точке O2, диаметр – отрезок BC.
- h (O1O2) – высота конуса; одновременно является высотой трапеции ABCD и осью симметрии обеих фигур.
Развёртка боковой поверхности усеченного конуса выглядит следующим образом:
Длина бОльшей (меньшей) дуги равна длине окружности соответствующего основания конуса ( 2πR или 2πr ).
📸 Видео
Задание 42. УСЕЧЕННЫЙ КОНУС. Часть 1Скачать

КАК НАЙТИ ДЛИНУ ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР ИЛИ РАДИУС? Примеры | МАТЕМАТИКА 6 классСкачать

Геометрия 11 класс (Урок№7 - Конус.)Скачать

Длина окружности. Площадь круга - математика 6 классСкачать

Конус. 11 класс.Скачать

№569. Радиусы оснований усеченного конуса равны R и r, где а образующая составляет с плоскостьюСкачать

Длина дуги окружности. 9 класс.Скачать

Простой расчёт развёртки конусаСкачать

ГЕОМЕТРИЯ 11 класс: Конус Площадь конуса. Усеченный конусСкачать

Усеченный конус ч.1 Развертка усечённого конуса.Скачать

Задание 42. УСЕЧЕННЫЙ КОНУС. Часть 2Скачать

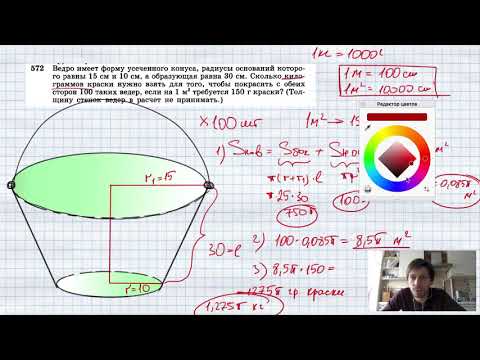
№572. Ведро имеет форму усеченного конуса, радиусы оснований которого равны 15 см и 10 см, а образуюСкачать