Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac) (;2π)) — четвертая четверть
- Почему так важно определять какой четверти принадлежит угол?
- Про непостоянство четвертей:
- Длина окружности
- Как найти длину окружности через диаметр
- Как найти длину окружности через радиус
- Как вычислить длину окружности через площадь круга
- Как найти длину окружности через диагональ вписанного прямоугольника
- Как вычислить длину окружности через сторону описанного квадрата
- Как найти длину окружности через стороны и площадь вписанного треугольника
- Как найти длину окружности через площадь и полупериметр описанного треугольника
- Как вычислить длину окружности через сторону вписанного правильного многоугольника
- Задачи для решения
- Площадь круга и его частей. Длина окружности и ее дуг
- Основные определения и свойства
- Формулы для площади круга и его частей
- Формулы для длины окружности и её дуг
- Площадь круга
- Длина окружности
- Длина дуги
- Площадь сектора
- Площадь сегмента
Видео:Как искать точки на тригонометрической окружности.Скачать

Почему так важно определять какой четверти принадлежит угол?
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .
Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.
Пример (ЕГЭ):
 ((0;-) (frac) ()) — четвертая четверть Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную. Видео:Тригонометрическая окружность. Как выучить?Скачать  Длина окружностиО чем эта статья: 6 класс, 9 класс, ЕГЭ/ОГЭ Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l Статья находится на проверке у методистов Skysmart. Видео:В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать  Как найти длину окружности через диаметрХорда — это отрезок, который соединяет две точки окружности. Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр: π— число пи — математическая константа, примерно равная 3,14 d — диаметр окружности Видео:Найти знак тригонометрической функции (bezbotvy)Скачать 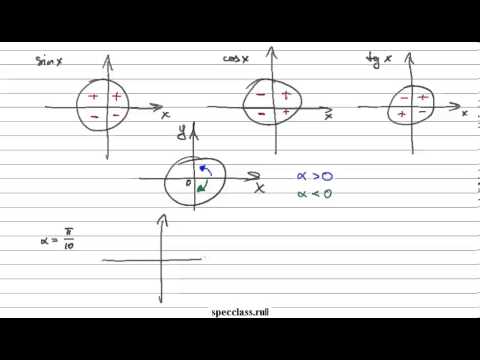 Как найти длину окружности через радиусРадиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус: π — число пи, примерно равное 3,14 r — радиус окружности Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур. Видео:Длина окружности. Математика 6 класс.Скачать  Как вычислить длину окружности через площадь кругаЕсли вам известна площадь круга, вы также можете узнать длину окружности: π — число пи, примерно равное 3,14 S — площадь круга Видео:Длина окружности. Площадь круга. 6 класс.Скачать  Как найти длину окружности через диагональ вписанного прямоугольникаКак измерить окружность, если в нее вписан прямоугольник: π — число пи, примерно равное 3,14 d — диагональ прямоугольника Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать  Как вычислить длину окружности через сторону описанного квадратаДавайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата: π — математическая константа, примерно равная 3,14 a — сторона квадрата Видео:Знаки тригонометрических функций. 9 класс.Скачать  Как найти длину окружности через стороны и площадь вписанного треугольникаМожно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь: π — математическая константа, она примерно равна 3,14 a — первая сторона треугольника b — вторая сторона треугольника c — третья сторона треугольника S — площадь треугольника Видео:Параллельные прямые | Математика | TutorOnlineСкачать  Как найти длину окружности через площадь и полупериметр описанного треугольникаМожно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр. Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два. π — математическая константа, примерно равная 3,14 S — площадь треугольника p — полупериметр треугольника Видео:Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать  Как вычислить длину окружности через сторону вписанного правильного многоугольникаРазбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата. Формула вычисления длины окружности: π — математическая константа, примерно равная 3,14 a — сторона многоугольника N — количество сторон многоугольника Видео:Деление окружности на 3; 6; 12 равных частейСкачать  Задачи для решенияДавайте тренироваться! Двигаемся от простого к сложному: Задача 1. Найти длину окружности, диаметр которой равен 5 см. Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу: Подставляем туда известные переменные и получается, что длина окружности равна Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм Решение. Радиус окружности равен Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи. Обучение на курсах по математике поможет закрепить полученные знания на практике. Видео:Разбор 31 варианта ОГЭ по математике 2024 / ПДФ решение + формулы / МатТаймСкачать  Площадь круга и его частей. Длина окружности и ее дуг
Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать  Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности Дуга |  Часть окружности, расположенная между двумя точками окружности Круг |  Конечная часть плоскости, ограниченная окружностью Сектор |  Часть круга, ограниченная двумя радиусами Сегмент |  Часть круга, ограниченная хордой Правильный многоугольник |  Выпуклый многоугольник, у которого все стороны равны и все углы равны Около любого правильного многоугольника можно описать окружность Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон. Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон. Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится. Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1. Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью: Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами. Видео:Вычисление значений тригонометрических функцийСкачать  Формулы для площади круга и его частей
где R – радиус круга, D – диаметр круга Площадь сектора | 
если величина угла α выражена в радианах
если величина угла α выражена в градусах Площадь сегмента | 
если величина угла α выражена в радианах
если величина угла α выражена в градусах Видео:Как запомнить тригонометрический круг специально ничего не выучивая?Скачать  Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга Длина дуги |  если величина угла α выражена в радианах
если величина угла α выражена в градусах Видео:Разбираем стереометрию за 6 часов | ЕГЭ по математике | Эрик ЛегионСкачать  Площадь кругаРассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1). Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 . Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 . Таким образом, площадь круга радиуса R , обозначаемая S , равна Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать  Длина окружностито, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство: откуда вытекает формула для длины окружности радиуса R : Следствие . Длина окружности радиуса 1 равна 2π. Видео:Формулы приведения - как их легко выучить!Скачать  Длина дугиРассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла. В случае, когда величина α выражена в градусах, справедлива пропорция из которой вытекает равенство: В случае, когда величина α выражена в радианах, справедлива пропорция из которой вытекает равенство: Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать  Площадь сектораРассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла. В случае, когда величина α выражена в градусах, справедлива пропорция из которой вытекает равенство: В случае, когда величина α выражена в радианах, справедлива пропорция из которой вытекает равенство: Площадь сегментаРассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла. Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем В случае, когда величина α выражена в в радианах, получаем |







 Подставим туда наши переменные и получим
Подставим туда наши переменные и получим 
 Основные определения и свойства. Число π
Основные определения и свойства. Число π




 ,
, ,
, ,
, ,
, ,
,
 ,
,



















