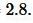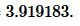С помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
- Высота треугольника. Определение
- Теорема о пересечении высот треугольника
- Высота треугольника по основанию и площади
- Высота треугольника по трем сторонам
- Высота треугольника по двум сторонам и радиусу описанной окружности
- Высота треугольника по стороне и прилежащему к ней углу
- Формулы для нахождения высоты треугольника
- Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
- Высота в прямоугольном треугольнике
- Высота в равностороннем треугольнике
- Примеры задач
- Высота треугольника
- Определение
- Как найти высоту треугольника?
- Через теорему Пифагора
- Через площадь треугольника
- Через тригонометрическую функцию
- Что мы узнали?
- 🔍 Видео
Видео:Вычисляем высоту через координаты вершин 1Скачать

Высота треугольника. Определение
Определение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
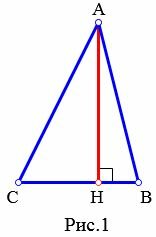 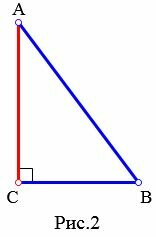 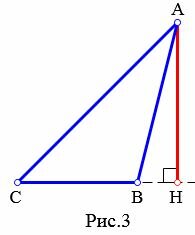 |
Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)).
Видео:В треугольнике ABC угол С=90, CH -- высота, AB=13, tgA=5. Найти BHСкачать

Теорема о пересечении высот треугольника
Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.
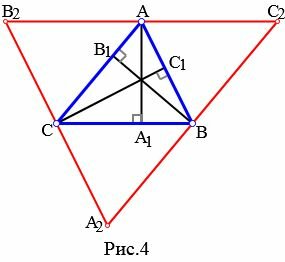 |
Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты ( small AA_1 ,) ( small BB_1 ,) ( small CC_1 ) пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник ( small A_2B_2C_2. ) Покажем, что точки ( small A, B, C ) являются серединами сторон треугольника ( small A_2B_2C_2. ) ( small AB=A_2C ) так как они являются противоположными сторонами параллелограмма ( small ABA_2C. ) ( small AB=CB_2 ) так как они являются противоположными сторонами параллелограмма ( small ABCB_2. ) Тогда ( small CB_2=CA_2, ) то есть точка ( small C ) является серединой стороны ( small A_2B_2 ) треугольника ( small A_2B_2C_2. ) Аналогично доказывается, что точки ( small A ) и ( small B ) являются серединами сторон ( small B_2C_2 ) и ( small A_2C_2, ) соответственно.
Далее из ( small AA_1⊥BC ) следует, что ( small AA_1⊥B_2C_2 ) поскольку ( small BC ǁ B_2C_2 ). Аналогично, ( small BB_1⊥A_2C_2, ) ( small CC_1⊥A_2B_2. ) Получили, что ( small AA_1,) ( small BB_1, ) ( small CC_1) являются серединными перпендикулярами сторон ( small B_2C_2, ) ( small A_2C_2, ) ( small A_2B_2, ) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.
Точка пересечения высот треугольника называется ортоцентром.
Видео:В треугольнике ABC BM – медиана и BH – высота ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Высота треугольника по основанию и площади
Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).
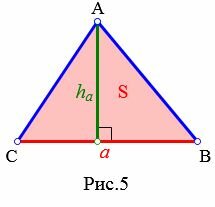 |
Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:
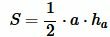 . . |
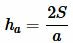 . . | (1) |
Пример 1. Сторона треугольника равна ( small a=5 ) а площадь ( small S=7. ) Найти высоту треугольника.
Применим формулу (1). Подставляя значения ( small a ) и ( small S ) в (1), получим:
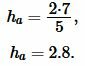 |
Ответ:
Видео:ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

Высота треугольника по трем сторонам
Формула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):
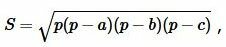 | (2) |
где ( small a, b, c ) стороны треугольника а полупериод ( small p ) вычисляется из формулы:
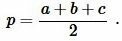 | (3) |
Высота треугольника, отпущенная на сторону ( small a) вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:
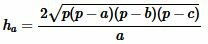 . . | (4) |
Пример 2. Известны стороны треугольника: ( small a=5, ) ( small b= 4, ) ( small c=7. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Найдем, сначала полупериод ( small p ) треугольника из формулы (3):
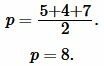 |
Подставляя значения ( small a , b, c ) и ( small p ) в (4), получим:
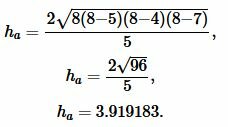 |
Ответ:
Видео:В треугольнике ABC проведены медиана BM и высота BH. Известно, что AC = 2 и BC = BM. Найдите AHСкачать

Высота треугольника по двум сторонам и радиусу описанной окружности
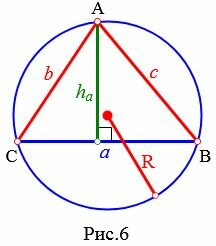 |
Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:
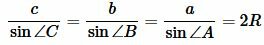 | (5) |
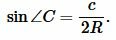 | (6) |
Далее, из теоремы синусов имеем:
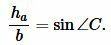 | (7) |
Подставляя (6) в (7), получим:
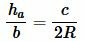 |
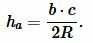 | (8) |
Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:
| (small max (b,c) ≤2R Пример 3. Известны стороны треугольника: ( small b=7, ) ( small c= 3 ) и радиус описанной окружности ( small R=4. ) Найти высоту треугольника, отпущенная на сторону ( small a. ) |
Решение: Проверим сначала условие (9):
| (small max (7,3) ≤2 cdot 4 Ответ: ( small 2frac. ) |
Видео:Задача 6 №27357 ЕГЭ по математике. Урок 46Скачать

Высота треугольника по стороне и прилежащему к ней углу
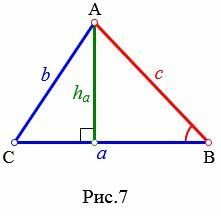 |
Найдем высоту ( small h_a ) треугольника на рисунке 7. Из теоремы синусов имеем:
| ( small frac=frac, ) |
| ( small h_a=c cdot sin angle B. ) | (11) |
Пример 4. Известны сторона ( small c=12 ) треугольника и прилежащий угол ( small angle B=30°. ) Найти высоту треугольника, отпущенная на сторону ( small a. )
Решение: Для нахождения высоты треугольника подставим значения ( small c=12 ) и ( small angle B=30° ) в (11). Имеем:
Видео:Досрочный ОГЭ Математика. Задание 16.Скачать

Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Видео:В треугольнике ABC BM – медиана и BH – высота ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Высота треугольника

Средняя оценка: 4.6
Всего получено оценок: 80.
Средняя оценка: 4.6
Всего получено оценок: 80.
Почти никогда не получится определить все параметры треугольника без дополнительных построений. Эти построения являются своеобразными графическими характеристиками треугольника, которые помогают определить величину сторон и углов.
Видео:16)В остроугольном треугольнике ABC проведена высота BH, угол BAC=48°. Найдите угол ABH. Ответ дайтеСкачать

Определение
Одной из таких характеристик является высота треугольника. Высота – это перпендикуляр, проведенный из вершины треугольника к его противоположной стороне. Вершиной называют одну из трех точек, которые вместе с тремя отрезками составляют треугольник.
Определение высоты треугольника может звучать и так: высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Это определение звучит сложнее, но оно точнее отражает ситуацию. Дело в том, что в тупоугольном треугольнике не получится провести высоту внутри треугольника. Как видно на рисунке 1, высота в этом случае получается внешней. Кроме того, нестандартной ситуацией является построение высоты в прямоугольном треугольнике. В этом случае, две из трех высот треугольника будут проходить через катеты, а третья от вершины к гипотенузе.
Как правило, высоту треугольника обозначают буквой h. Также обозначается высота и в других фигурах.
Видео:В треугольнике ABC AC=BC=27, AH — высота, sin BAC= 2/3 . Найдите BH.Скачать

Как найти высоту треугольника?
Существует три стандартных способа нахождения высоты треугольника:
Через теорему Пифагора
Этот способ применяется для равносторонних и равнобедренных треугольников. Разберем решение для равнобедренного треугольника, а потом скажем, почему это же решение справедливо для равностороннего.
Дано: равнобедренный треугольник АВС с основанием АС. АВ=5, АС=8. Найти высоту треугольника.
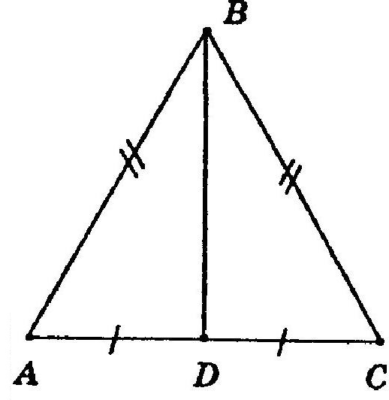
Для равнобедренного треугольника важно знать, какая именно сторона является основанием. Это определяет боковые стороны, которое должны быть равны, а так же высоту, на которую действую некоторые свойства.
Свойства высоты равнобедренного треугольника, проведенной к основанию:
- Высота совпадает с медианой и биссектрисой
- Делит основание на две равные части.
Высоту обозначим, как ВD. DС найдем как половину от основания, так как высота точкой D делит основание пополам. DС=4
Высота – это перпендикуляр, значит ВDС – прямоугольный треугольник, а высота ВD является катетом этого треугольника.
Найдем высоту по теореме Пифагора: $$BD=sqrt=sqrt=3$$
Любой равносторонний треугольник является равнобедренным, только основание у него равно боковым сторонам. То есть, можно использовать тот же порядок действий.
Через площадь треугольника
Этим способом можно пользоваться для любого треугольника. Чтобы им воспользоваться, нужно знать значение площади треугольника и стороны, к которой проведена высота.
Высоты в треугольнике не равны, поэтому для соответствующей стороны получится вычислить соответствующую высоту.
Формула площади треугольника: $$S=*bh$$, где b – это сторона треугольника ,а h – высота, проведенная к этой стороне. Выразим из формулы высоту:
Если площадь равна 15, сторона 5, то высота $$h=2*=6$$
Через тригонометрическую функцию
Третий способ подойдет, если известна сторона и угол при основании. Для этого придется воспользоваться тригонометрической функцией.
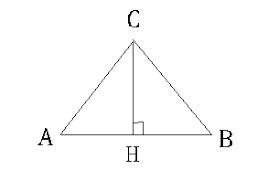
Угол ВСН=30 градусам , а сторона BC=8. У нас все тот же прямоугольный треугольник BCH. Воспользуемся определением косинуса угла прямоугольного треугольника. Косинус острого угла – это отношение прилежащего катета к гипотенузе, значит: BH/BC=cos BCH, а угол BCH равен 60 градусам, так как сумма острых углов прямоугольного треугольника равна 90 градусам.
Угол известен, как и сторона. Выразим высоту треугольника:
Значение косинуса в общем случае берется из таблиц Брадиса, но значения тригонометрических функций для 30,45 и 60 градусов – табличные числа.
Видео:В треугольнике ABC AC = BC, AH – высота, AB = 5, sinBAC = 7/25 . Найдите BH.Скачать

Что мы узнали?
Мы узнали, что такое высота треугольника, какие бывают высоты и как они обозначаются. Разобрались в типовых задачах и записали три формулы для высоты треугольника.
🔍 Видео
№492. Найдите высоты треугольника со сторонами 10 см, 10 см и 12 см.Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Высота в прямоугольном треугольнике. 8 класс.Скачать

Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

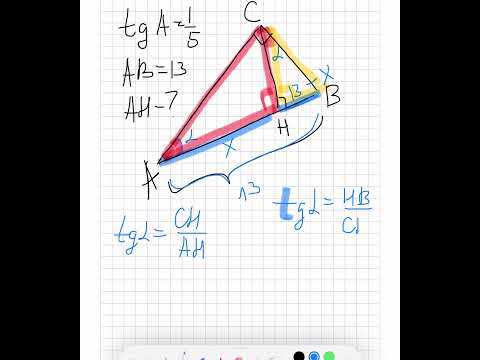
В треугольнике ABC угол C равен 90°, CH – высота, AB = 13, тангенс A =1/5. Найдите AH.Скачать
15 задание ОГЭ по математике 2023 Треугольник Shorts #shorts #огэпоматематике2023 #треугольникСкачать