Как найти 30 градусов на окружности циркулем

Математика — это очень просто, даже проще, чем мы можем себе представить. Сложной математику делают сами математики.

Страницы

воскресенье, 20 октября 2013 г.

Простое построение углов

Тут мне в комментариях задали интересный вопрос. Простое построение углов — как это сделать? Вот сам вопрос.

Вопрос о построении углов

И так, вопрос сводится к следующему — в декартовой системе координат, если брать одинаковый икс и игрек, получим прямую под углом в 45 градусов к осям координат. А как построить углы другой величины? Можно, конечно, заняться гаданием на кофейной гуще и попробовать высчитать, сколько нужно откладывать по иксам, сколько по игрекам, чтобы получился другой удобочитаемый угол. Не 156пи/911, а что-то типа 1, 5, 10, 15 градусов.

Угол в тридцать градусов получается, когда по оси игрек мы возьмем половинку, а расстояние от центра системы координат до точки будет равно единице. При помощи циркуля и линейки такое построить можно, но.

Построение угла в 30 градусов

Для подобного построения необходимо: построить декартову систему координат, нарисовать круг, по оси игрек разделить радиус пополам, через полученную точку провести линию, параллельную заданной. Фокус в том, что о декартовой системе координат древние люди не имели ни малейшего понятия. И ведь тысячелетиями как-то жили, и углы строили.

И так, четвертое-пятое тысячелетие до нашей эры, древняя Месопотамия. Тогда зародилось то, чем мы пользуемся и сегодня. Астрономия, письменность, математика, углы. Какими инструментами тогда пользовались для построения углов? Линейка, циркуль. Возможно, были тогда и угольники, хотя это не принципиально — для построения прямого угла достаточно циркуля и линейки.

Теперь попробуем строить углы при помощи циркуля и линейки без всяких координатных систем. Проводим прямую линию, строим окружность с центром на построенной линии. Ставим циркуль в точки пересечения линии и окружности и строим две окружности того же радиуса. Соединяем линиями центр первой окружности точки пересечения окружностей. У нас получились углы в 60 градусов.

Построение угла в 60 градусов

Почему возле углов я поставил циферки 1, 2, 3, 4, 5, 6? Я считаю, что именно такую единицу измерения углов использовали наши предки. Назовем эту единицу измерения углов «вавилонский угол». Дальше один угол делится на 60 градусов. Почему именно на 60? В те времена, в тех местах, использовалась шестидесятеричная система счисления. Вы такой системой счисления никогда не пользовались и понятия о ней не имеете? Ошибаетесь. Когда вы выражаете время в минутах и секундах, вы используете именно шестидесятеричное счисление. «Подожди пять минут» в переводе на десятичные дроби, если за единицу брать один час, будет звучать как «Подожди 0,083333333. часа». Дико звучит, не правда ли?

Давайте посмотрим на структуру вавилонских шестидесятеричных чисел. Единицу целого числа вавилоняне делили на шестьдесят частей. Потом каждую эту часть делили ещё на шестьдесят частей и так дальше. У шестидесятых долей были свои названия: минута, секунда, терция.

Минута, секунда, терция, кварта, квинта

Вот теперь я включаю логику и начинаю рассуждать. Если минута — это малая часть, значит могла быть и большая часть или просто часть. Градус как нельзя лучше подходит на роль части вавилонского угла. Тогда первый шестидесятеричный знак после запятой будет называться градус и только второй — минута. Хотя, я могу и ошибаться. Вполне возможно, что градус играет роль целого числа, а придуманный мною «вавилонский угол» — ни что иное, как аналог наших десятков. Но суть не в этом.

Я просто хотел обратить ваше внимание на то, что 360 градусов окружности приблизительно равны 365 дням в году (если отбросить градусы и дни, а тупо сравнивать только числа, как это любят делать наши математики). Почему я сравниваю окружность с днями в году? За сутки Солнце смещается по эклиптике приблизительно на один градус. С другой стороны, вавилонский угол в 60 градусов приблизительно равен одному радиану. Ведь 1 радиан ≈ 57,295779513° ≈ 57° 17′ 44,806″ При этом, у вавилонского угла есть точное числовое значение, а вот радиан точного числового значения не имеет — он построен на бесконечности числа «пи». Один — ноль в пользу древних математиков. Что бы там не утверждали наши математики, но принимать в качестве единицы измерения бесконечное число — это не совсем разумно. Думаю, физики меня поймут — создать точный измерительный прибор для измерения неточной величины даже теоретически невозможно.

Но продолжим наши построения углов. Через центр первой окружности проводим перпендикуляр, затем строим ещё две окружности с центрами в точках пересечения перпендикуляра и первой окружности.

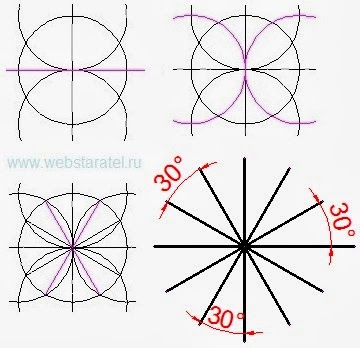Построение угла в 30 градусов

Получился угол в 30 градусов. Как видите, построение очень простое, даже циркуль с переменным радиусом не нужен. Достаточно отрезать кусок разветвления ветки вместо циркуля и всё прекрасно получится. В этой первозданной простоте родились наши современные часы.

Вавилонские углы и циферблат часов

Как видно из рисунка, один час времени равняется тридцати градусам угла. Одна минута времени равна шести градусам угла. В минуте шесть градусов, в окружности шесть углов — что-то в этом есть. Вот только часов на окружности циферблата 12, что не очень вписывается в логику шестидесятеричной системы счисления. У наших математиков везде тупо было бы шестьдесят. В году двенадцать знаков зодиака, в сутках 24 часа. Где-то должна быть очень веская логика именно такого построения временной шкалы. Я не занимался изучением этого вопроса, древние вавилоняне меня и без него шокировали. Но об этом в следующей статье.

Особо стоит отметить, что в древности использовались солнечные часы. Было два варианта солнечных часов — напольные и настенные. Так вот, стрелки этих двух типов часов (тень на циферблате) двигались в противоположных направлениях — по часовой стрелке у напольных и против часовой стрелки у настенных. Можно предположить, что такого понятия, как «вращение по часовой стрелке» у древних математиков не существовало. А в том, что древние люди были очень умными, мы можем убедиться, рассмотрев загадку вавилонской таблички.

Деление окружности на градусы

Во всем мире принято странное деление окружности на 360 градусов. Со всех точек зрения было бы логичнее деление окружности на 2, потом на 4, потом на 8, 16, 32, 64 и т. д. части. А то поди ж ты: сначала делим окружность на 4 части, потом каждую четверть на 90 градусов. Почему на 90? Почему не на 100 или 120? Оказывается, деление окружности на 360 градусов ведет свое начало от вавилонских жрецов. Они, наблюдая за движением Солнца, обнаружили, что в день равноденствия Солнце от восхода до заката описывает на небесном своде полуокружность, в которой видимый поперечник Солнца укладывается ровно 180 раз. Поэтому-то они и стали каждую полуокружность делить на 180 частей, а каждую окружность – на 360 градусов! Школьный транспортир напоминает, что каждое его деление есть не что иное, как отпечаток – след Солнца, проходящего по небосклону в день равноденствия.

Существует, правда, египетская гипотеза происхождения деления окружности. Длительность года у египтян составляла 360 дней. Год был разбит на 12 месяцев, а каждый месяц на 30 дней. И Солнце по небу проходило каждый год через 12 зодиакальных созвездий. Так что Солнце находилось в каждом из этих созвездий по 30 дней. Итак, за 1 день солнце проходит по небу расстояние в 1 единицу пути. Таких единиц всего 360. И только потом эту единицу пути назвали градусом.

Герой романа Жюля Верна «Таинственный остров» инженер Сайрес Смит, чтобы определить величину острого угла, образованного ножками самодельного циркуля, «измерил этот угол по окружности, разделённой на триста шестьдесят равных частей; угол равнялся десяти градусам». Зачем для измерения острого угла потребовалось делить на части всю окружность, когда достаточно рассмотреть её четверть, непонятно, и как удалось добиться их равенства? Поэтому, деление окружности непростой вопрос, которому во многих задачах стоит уделить время.

Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.

Содержание

Градус [ править | править код ]

Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.

Причина выбора градуса как единицы измерения углов неизвестна. Одна из теорий предполагает, что это связано с тем, что 360 — приблизительное количество дней в году [1] . Некоторые древние календари, такие как древнеперсидский, использовали год в 360 дней.

Другая теория гласит, что аккадцы (вавилоняне) поделили окружность, используя угол равностороннего треугольника как базу и поделив результат на 60, следуя своей шестидесятеричной системе счисления [2] [3] .

Если построить окружность радиусом 57 см, то 1 градус будет примерно соответствовать 1 см длины дуги данной окружности.

Градус в альтернативных единицах измерения:

1 ∘ = 2 π 360 = >>> радиан = π 180 = 1 p ≈ 1 57,295 779513 ∘ >>= >approx 295779513^ >>>> [4] ≈ 0,017 4532925 0174532925> (радиан в 1°) 1 ∘ = 1 360 = >> оборота=0,002(7) оборота=0,002777777777… 1 ∘ = 400 360 = >> градов=1,(1) градов=1,11111111111… градов

Минуты и секунды [ править | править код ]

По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается штрихом x′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается двумя штрихами y″. Ранее употреблялась величина в 1/60 секунды — терция (третье деление), с обозначением тремя штрихами — z″′. Деление градуса на минуты и секунды ввёл Клавдий Птолемей [5] ; корни же такого деления восходят к учёным Древнего Вавилона (где использовалась шестидесятеричная система счисления).

Минуты и секунды в других системах измерения:

1 ′ = 2 π 360 ∘ ⋅ 60 ′ = 1 ′ p ′ ≈ 1 ′ 3437,747 ′ >cdot 60′>>= 747′>>> [4] ≈ 2,908 88208 ⋅ 10 − 4 rad 90888208cdot 10^

>> (1 минута в радианах) 1 ″ = 2 π 360 ∘ ⋅ 60 ′ ⋅ 60 ″ = 1 ″ p ″ ≈ 1 ″ 206264 , 8 ″ >cdot 60’cdot 60”>>= >approx 8”>>> [4] ≈ 4,848 136811 ⋅ 10 − 6 rad 848136811cdot 10^

>> (1 секунда в радианах).

Минуты и секунды в радианной мере из-за своих чрезмерно малых величин представляют ограниченный интерес и практически очень мало используются.
Гораздо больший интерес представляет перевод десятичных (сотых, десятитысячных) долей градуса в минуты и секунды и обратно — см. Радиан#Связь радиана с другими единицами и Географические координаты.

Угловая секунда [ править | править код ]

Углова́я секу́нда (англ. arcsecond , arc second , as , second of arc ; синонимы: дуговая секунда, секунда дуги [6] ) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла [7] .

Использование [ править | править код ]

Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается s ). Соотношение между этими величинами определяется формулой 1 s =15″. [8]

Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой [6] [9] , что является простой транслитерацией с англ. arcsecond .

Дольные единицы [ править | править код ]

По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. milliarcseconds , mas ), микросекунды (англ. microarcseconds , µas ) и пикосекунды (англ. picoarcseconds , pas ). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению [7] . Однако согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками [10] , в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т. п.), либо к угловым секундам, либо обозначаться исходными единицами ( mas , µas и pas соответственно).

Связь различных угловых единиц измерения

Единица	Величина	Обозначение	Аббревиатура	Радиан (прибл.)
градус	1/360 окружности	°	deg	17,4532925 mrad
минута	1/60 градуса	′	arcmin, amin, ′ ^ >> , MOA	290,8882087 µrad
секунда	1/60 минуты	″	arcsec	4,8481368 µrad
миллисекунда	1/1000 секунды	mas	4,8481368 nrad
микросекунда	1 × 10 −6 секунды	μas	4,8481368 prad

Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.

Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника. [ источник не указан 2692 дня ]

В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP) [11] [12] .

Главная ≫ Инфотека ≫ Математика ≫ По следам вавилонян, или почему в окружности 360 градусов? // Наталья Карпушина

Знаете ли вы, почему в окружности 360 градусов, а не 180 или, скажем, не 300? Откуда пошла традиция делить окружность на равные части и почему было выбрано именно такое их число? Оказывается, этому делению мы обязаны вавилонянам. Согласно их календарю, продолжительность года составляла 360 дней — именно столько раз, по наблюдениям древних астрономов, солнечный диск укладывался на годичном пути светила. Иными словами, за каждые сутки солнце делало один «шаг». Поэтому вавилоняне и разделили окружность на 360 равных частей, каждую из которых называют градусом (от лат. gradus — шаг, ступень). Считается, что они же изобрели простейший инструмент для измерения углов − транспортир. Но вот вопрос: как же древние сумели разделить окружность на равные части, не владея техникой геометрических построений и располагая лишь примитивными инструментами? Загадка…

С подобной проблемой однажды столкнулся инженер Сайрес Смит, герой романа Жюля Верна «Таинственный остров». Чтобы определить величину острого угла, образованного ножками самодельного циркуля, он «измерил этот угол по окружности, разделённой на триста шестьдесят равных частей; угол равнялся десяти градусам». Вот, собственно, и всё, что сообщает о решении данной задачи Жюль Верн. Непонятно, зачем для измерения острого угла потребовалось делить на части всю окружность, когда достаточно рассмотреть её четверть, и уж совсем неясно, как удалось добиться их равенства. Можно лишь предположить, что инженер выполнял построения на земле с помощью подручных средств, как он не раз поступал при решении других практических задач, если те требовали знания геометрии.

Сначала прикинем решение на бумаге. Для того чтобы разделить окружность на равные части, пригодится диск, край которого представляет собой окружность фиксированной длины l . Если катить диск по нарисованной на земле окружности длиной L = nl , где n = 2, 3, 4 …, то через n оборотов он обежит линию и вернётся в исходную точку. Пришло время проявить смекалку: сделаем на краю диска «острый выступ», оставляющий на земле отметку после каждого оборота. С его помощью мы разметим окружность, то есть разобьём на равные части. Допустим, нужно разделить окружность на дуги по 10°. В таком случае n = 360° : 10° = 36. Так как L превосходит l в 36 раз, то из соображений подобия и радиус R нарисованной на земле окружности должен быть во столько же раз больше радиуса r диска.

Теперь можно переходить к конкретным действиям. Измерим радиус диска. Пусть для определённости r = 5 см, тогда R = 180 см. Сделаем в диске отверстие по линии радиуса и вставим в него, например, кусочек спицы так, чтобы острый конец чуть торчал наружу. Отмерим кусок верёвки длиной 180 см и привяжем к его концам по колышку. Один колышек вобьём в землю, затем натянем верёвку и, удерживая её в таком состоянии, очертим другим колышком окружность. Наконец, прокатим по нарисованной линии диск; 36 меток (следов спицы) разделят окружность на дуги по 10° в каждой. Задача решена. Ясно, что в общем случае, подбирая подходящую длину радиуса R и количество «зарубок» на диске, легко разделить окружность на нужное число равных частей.

Задачу можно решить и по-другому, как делали древние египтяне, строя прямой угол при помощи верёвки, разделённой узелками на равные части. За единицу измерения примем длину диска. Обмотаем верёвку вокруг диска и завяжем на конце отмеренного отрезка узелок. Проделаем ту же операцию необходимое число раз. Затем положим размеченную таким образом верёвку поверх нарисованной на земле окружности (узелки соответствуют меткам, которые оставил бы на земле катящийся диск в первом способе построения). В данном случае при вычерчивании окружности можно обойтись без рулетки: радиус R окружности получим, отложив на верёвке диаметр диска n /2 раз (при нечётном n придётся добавить длину радиуса).

Проигрывая в точности построений, мы вместе с тем выигрываем в их простоте и доступности, что на практике зачастую ценится больше. Добавим, что верёвка с узелками — это примитивный циркуль, который используется до сих пор, когда надо провести на земле дугу большого радиуса, например при разметке спортивной арены, или очертить круг при разбивке клумбы.

Как построить угол в 30 градусов с помощью циркуля и линейки?

Рисуешь прямой угол. На одном катете метишь один радиус, на другом -два. Соединяешь и готово. Давно из школы, если ошибся-поправте.

Таня, вот план действий: 1)чертишь с помощью циркуля и линейки перпендикуляр (ты умеешь)
2)ты должна задать нижний катет и гипотенузу (гипотенуза в 2раза больше катета
3)соединяешь
А от сюда идет и угол в 105, 150 и т. д.
таким образом у тебя выходит треугольник в котором верхний угол равен 30 градусов! УДАЧИ=*

Начерти прямой угол .Сделай циркулем дугу в любом месте прямого угла. Раздели эту дугу на три равных части .Приложи линейку и проведи прямую, через одну из точек .

🌟 Видео

Комментарии: 0