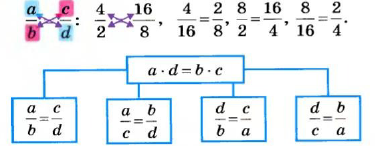
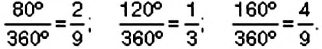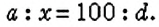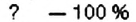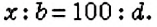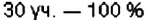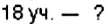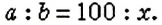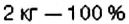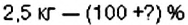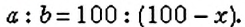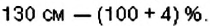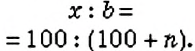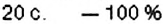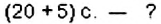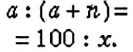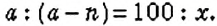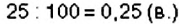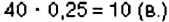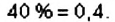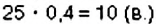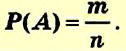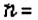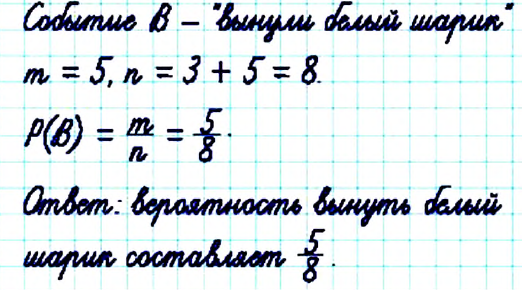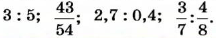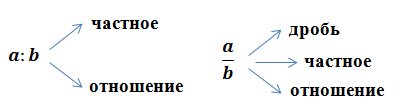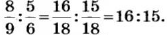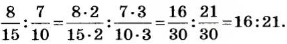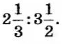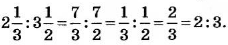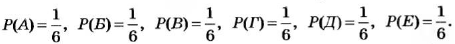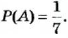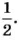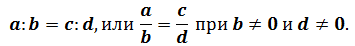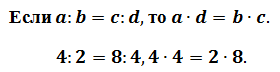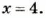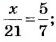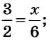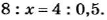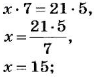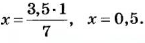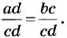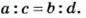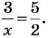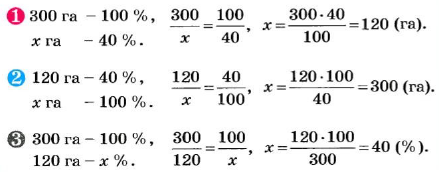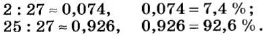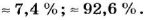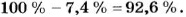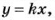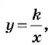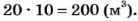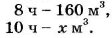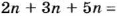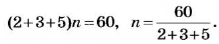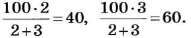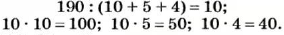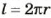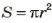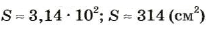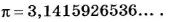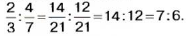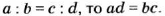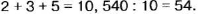Содержание:
- Отношения и пропорции
- Отношение. Основное свойство отношения
- Случайные события
- Вероятность случайного события
- Пропорция
- Прямая пропорциональная зависимость
- Процентное отношение
- Процентные расчеты
- Окружность. Длина окружности
- Круг. Площадь круга
- Столбчатые и круговые диаграммы
- Отношения и пропорции
- Отношение и его свойства
- Основное свойство отношения
- Пропорция и её свойства
- Основное свойство пропорции
- Правила нахождения неизвестного члена пропорции
- Прямая и обратная пропорциональные зависимости
- Деление числа в данном отношении
- Пропорциональное деление
- Масштаб
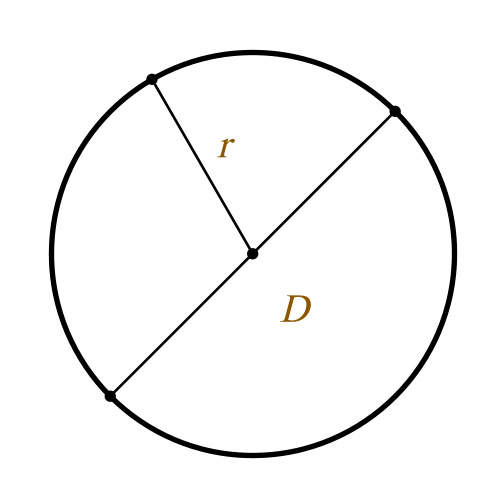
- Окружность и круг. Круговой сектор
- Формула диаметра окружности
- Формула длины окружности
- Формула площади круга
- Диаграммы
- Цилиндр. Конус. Шар
- Процентные расчёты
- Нахождение процента от числа
- Нахождение числа по его проценту
- Нахождение процентного отношения двух чисел
- Нахождение изменения процента по изменению числа
- Нахождение числа по его процентному изменению
- Нахождение процентного отношения двух чисел по изменению числа
- Вероятность случайного события
- Отношения и пропорции
- Отношения
- Пример №43
- Пример №44
- Пример №45
- Вероятность случайного события
- Пропорции
- Пример №46
- Пример №47
- Процентное отношение
- Пример №48
- Пример №49
- Пример №50
- Пропорциональные величины
- Пример №51
- Пример №52
- Задачи на пропорциональное деление
- Пример №53
- Пример №54
- Окружность и круг
- Пример №55
- Диаграммы
- Пример №56
- Пример №57
- Длина окружности
- Формула расчёта длинны окружности
- Пример нахождения длинны окружности
- Длина окружности и площадь круга. Урок в 6-м классе
- 1. Практическая работа по теме «Длина окружности и площадь круга». 6 класс
- 2. Практические задачи
- 1. Организационный момент (1-2 минуты)
- 2. Постановка цели и мотивация (3-5 минут)
- Практическая работа №1 (15 минут)
- 📽️ Видео
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Отношения и пропорции
Отношение. Основное свойство отношения
Пример:
Для класса закупили 90 тетрадей, из них 60 — в клетку, а остальные — в линейку Во сколько раз всех тетрадей больше, чем тетрадей в клетку? Какую часть всех тетрадей составляют тетради в клетку?
Решение:
Чтобы найти, во сколько раз всех тетрадей больше, чем тетрадей в клетку, нужно 90 разделить на 60, го есть найти частное чисел 90 и 60:
Итак, всех тетрадей в 1,5 раза больше, чем тетрадей в клетку. Частное чисел 90 и 60 показывает, но сколько раз число 90 больше числа 60.
Ответим на второй вопрос задачи. Так как всего есть 90 тетрадей, то 1 тетрадь — это 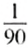
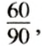
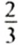
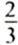
Чтобы ответить на оба вопроса задачи, нам пришлось искать частное двух чисел Такие частные называют отношениями двух чисел: частное 90:60= 1,5 называют отношением числа 90 к числу 60; частное 60:90= 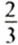
Отношением двух чисел называют частое этих чисел. Отношение показывает, во сколько раз одно число больше другою или какую часть составляет одно число от другого.
Если имеются две величины, измеренные одной и той же единицей измерения, то отношением этих величин называют отношение их числовых значений.
Например, отношение 6 км к 10 км равно 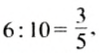
Так как отношение является частным, а частное не изменяется, если делимое и делитель умножить или разделить на одно и то же число, отличное от нуля, то отношение не изменится, если каждое из чисел отношения умножить или разделить на одно и то же, отличное от нуля, число. Это свойство называют основным свойством отношения. Например:
На основании этого свойства можно заменить отношение дробных чисел отношением натуральных чисел. Например:
Пример:
Спортсмен пробежал 100 м за 10 с, а ракета пролетела 24 км за 3 с. Во сколько раз скорость ракеты больше скорости спортсмена?
Решение:
1) 100 : 10= 10 (м/с) — скорость спортсмена.
2) 24 : 3 = 8 (км/с) — скорость ракеты.
Найдем скорость ракеты в м/с: 8 км/с = 8000 м/с.
3) 8000 : 10 = 800 (раз).
Ответ. В 800 раз.
Случайные события
Мы часто слышим, а иногда говорим: «это возможно», «это невозможно», «этого никогда не будет», «это обязательно случится», «это маловероятно» и т. д. Наверное, сегодня будет дождь; возможно, завтра я пойду в лес; вероятно, этот мультфильм будет интересным и т. д. Так мы говорим тогда, когда речь идет о наступлении события, которое в одних и тех же условиях может произойти или не произойти. Такое событие называют случайным.
Пример 1. В корзине есть красные и зеленые яблоки. Не заглядывая в корзину, наугад вынимаем одно яблоко. Можно ли заранее сказать, какого цвета будет яблоко?
Конечно, нет. Можетпроизойти одно из двух случайных событий: «взятое яблоко окажется красным», «взятое яблоко окажется зеленым».
Пример 2. В корзине 7 красных и 2 зеленых яблока. Не заглядывая в корзину, наугад берут из нее одно яблоко. Можно ли заранее сказать, какого цвета будет яблоко?
Мы уже знаем, что заранее сказать, какого цвета будет яблоко, невозможно, но, скорее всего, яблоко будет красным, потому что их в корзине больше. Взять красное яблоко из корзины в этом случае более вероятно, чем зеленое.
Пример 3. В корзине есть 3 красных и 3 зеленых яблока. Не заглядывая в корзину, наугад берут из нее одно яблоко. Какое из событий может произойти: А — «взяли красное яблоко»; В — «взяли желтое яблоко»; С — «взяли зеленое яблоко»; D — «взяли яблоко»?
Из корзины можно взять только то, что в ней есть, поэтому вынуть из корзины желтое яблоко невозможно. Поэтому событие В «взяли желтое яблоко» при данных условиях невозможно.
Так как в корзине есть только яблоки, то любой предмет, вынутый из корзины, является яблоком. Итак, при данных условиях событие D «взяли яблоко» произойдет обязательно. Говорят, что это событие является достоверным.
События А и С при данных условиях являются случайными, поскольку взятое яблоко может быть как красным, так и зеленым. Так как красных и зеленых яблок в корзине поровну, то эти случайные события являются равновероятными.
Пример:
Игральным кубиком называют кубик, на грани которого нанесены числа 1, 2, 3,4, 5 и 6, обозначенные соответствующим количеством точек (рис. 4). Какое из событий после подбрасывания игрального кубика является более вероятным:
а) А: «выпадет число 3» или В: «не выпадет число 3»;
б) С: «выпадет четное число» или D: «выпадет нечетное число»?
Решение:
а) Событие А произойдет только в одном случае — если выпадет число 3. Событие В произойдет в пяти случаях если выпадет число 1, 2, 4, 5 или 6. Поэтому событие В является более вероятным.
б) Событие С произойдет в трех случаях — если выпадет число 2, 4 или 6. Событие D произойдет также в трех случаях — если выпадет число 1, 3 или 5. Поэтому события С и D являются равновероятными.
Интересные рассказы
О случайных событиях
На первый взгляд может показаться, что никаких законов для случайных событий быть не может — на то они и случайные. Однако, если подумать как следует, можно придти к выводу, что и случайные события имеют некоторые закономерности.
Рассмотрим пример. Представим себе, что мы подбрасываем монету и фиксируем, что выпадет — «орел» или «решка» Подбросив монету один раз, нельзя предугадать, какой стороной она упадет. Но если подбросить ее тысячу раз подряд, то уже можно сделать некоторые выводы о том, сколько раз выпадет «орел», а сколько — «решка».
В XVIII веке эксперименты с монетой проводил французский естествоиспытатель Жорж Луи де Бюффон (1707 — 1788), у которого во время 4040 подбрасываний «орел» выпал 2048 раз. В начале XX века английский математик Карл Пирсон провел 24 000 подбрасываний, и «орел» выпал 12 012 раз.
Оба эксперимента дают похожие результаты: подбрасывая многократно монету, появление «орла» наблюдали приблизительно в половине всех подбрасываний, то есть частота появления «орла» приблизительно равна 0,5. Итак, хотя каждый результат подбрасывания монеты является случайным событием, многократно повторяя эксперимент, можно наблюдать указанную закономерность.
Рассмотрим еще один пример. Когда в семье должен родиться ребенок, никто не может заранее предугадать, будет это мальчик или девочка. Но во всех странах и у всех народов на 1000 новорожденных в среднем приходится 511 мальчиков и 489 девочек. Эту закономерность отмечали многие ученые, среди них был и создатель теории вероятности — французский математик Пьер Симон Лаплас (1749 — 1827).
Вероятность случайного события
Вы уже знаете, что случайные события могут быть более вероятными, менее вероятными, равновероятными, то есть случайное событие можно охарактеризовать понятием вероятность. Какими числами можно оценивать вероятность? Понять это помогут следующие примеры.
Пример 1. На столе лежит 8 внешне одинаковых тетрадей, из них одна в клетку, а остальные — в линейку. Ученик хочет взять тетрадь в клетку. Имеется 8 равновероятных случаев взять тетрадь, и только в одном из них она будет в клетку. Поэтому считают, что вероятность того, что взятая наугад тетрадь будет тетрадью в клетку, равна
Отношение 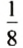
Пример 2. В лотерею разыгрывается 1000 билетов, из них 10 — выигрышные. Какова вероятность того, что купленный лотерейный билет будет выигрышным?
Имеем 1000 равновероятных случаев купить билет лотереи, и только в 10 случаях он будет выигрышным. Отношение 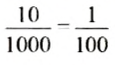
Пример 3. В урне 7 белых и 3 красных шара. Не заглядывая в урну, наугад вынимают 1 шар. Вероятность того, что вынули белый шар, равна 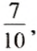
Отношение 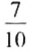
цвета, а отношение 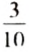
Вероятность невозможного событии равна 0, а достоверного — 1.
Пример:
Найти вероятность того, что после подбрасывания игрального кубика выпадет число 3; число 10.
Решение:
После подбрасывания игрального кубика может выпасть любое из шести чисел — 1, 2, 3, 4, 5 или 6, то есть возможны 6 разных случаев, и только в одном из них выпадет число 3. Поэтому вероятность того, что после подбрасывания игрального кубика выпадет число 3, равна 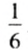
Пример:
На полке стоит 10 учебников, 15 томов художественных произведений и 3 справочника. Наташа наугад берет одну книгу. Какова вероятность того, что эта книга: а) является учебником; б) не является учебником?
Решение:
а) Учебников на полке 10, а всего книг— 10 + 15 + 3 = 28. Поэтому вероятность того, что взятая книга является учебником, равна 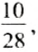
б) Не учебников (других книг) 15 + 3=18, всего книг — 28. Поэтому вероятность того, что взятая книга не является учебником, равна 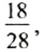
Пропорция
Найдите отношение чисел: 36 к 9; 24 к 6. Сравните эти отношения.
Эти отношения равны, а поэтому можно записать:
Равенство двух отношений называют пропорцией.
С помощью букв пропорцию можно записать так:
Эти записи читают:
«отношение а к b равно отношению с к d»,
«а, деленное на b, равно с, деленному на d»,
«а относится к b, как с относится к d».
В пропорции 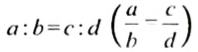
Далее будем считать, что все члены пропорции отличны oт нуля.
Пропорция 36 : 9 = 24 : 6 верная, так как значением ее левой и правой частей является одно и то же число 4.
Найдите произведения крайних и средних членов этой пропорции. Сравните их.
В верной пропорции произведение крайних членов равно произведению средних членов.
Это свойство называют основным свойством пропорции.
Итак, если пропорция 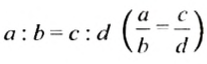
Верно и наоборот: если произведение крайних членов пропорции равно произведению средних членов, то эта пропорция верная.
Для верной пропорции 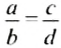
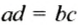
где а и d — крайние члены пропорции, bс — произведение средних членов пропорции.
Чтобы найти крайний член пропорции, нужно произведение ее средних членов разделить на другой крайний член.
Чтобы найти средний член пропорции, нужно произведение ее крайних членов разделить на другой средний член.
Для тех, кто хочет знать больше
Из основного свойства пропорции следует, что если в верной пропорции поменять, местами средние члены или крайние члены, то получим новые верные пропорции.
Так, если пропорция 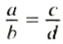
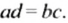
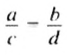
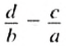
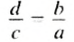
так как в каждой из них произведение 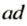
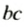
Если 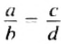
Пример:
Найти неизвестный член пропорции
Решение:
По правилу нахождения среднего члена пропорции имеем:
Пример:
Решить уравнение:
Решение:
Интересные рассказы
Пропорция и музыка
Слово «пропорция» (от латинского proportio) означает «соразмерность», «некоторое отношение частей между собой».
С помощью пропорций решали задачи еще в древние времена. Полная теория пропорций была создана в Древней Греции в IV в. до н. ч., в основном в работах ученых Эвдокса Книдского и Теэтета.
Теория пропорций в совершенстве изложена в «Началах» Эвклида, в частности там дано доказательство основного свойства пропорции
Древние греки называли учение об отношениях и пропорциях музыкой, которую считали областью математики. Они знали, что слабо натянутая струна 122 звучит ниже («толще»), а сильно натянутая струна лает более высокий звук. Но в каждом струнном музыкальном инструменте не одна, а несколько струн. Чтобы все струны во время игры звучали «согласованно», приятно для слуха человека, их длины (а при условии одинаковой длины — толщины) должны находиться в определенном отношении. Поэтому учение об отношениях и пропорциях древние греки называли музыкой.
Пропорциональность использовалась и используется сегодня в искусстве, архитектуре. Использование пропорционапьности в архитектуре, живописи, скульптуре означает соблюдение определенных соотношений между отдельными частями сооружения, картины, скульптуры и т. п.
Современную запись пропорции 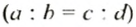
Прямая пропорциональная зависимость
Пример:
Три метра ткани стоят 60 руб. Сколько стоят 6 м этой же ткани?
Решение:
Пойдите два способа решения задачи.
I способ
1) 60 : 3 = 20 (руб.) — стоит 1 м ткани.
2) 20 • 6 — 120 (руб. ) — стоят 6 м ткани
II способ
1) 6 : 3 = 2 — во сколько раз увеличилось количество ткани.
2) 60 • 2 = 120 (фн.) — стоят 6 м ткани (стоимость увеличилась в два раза).
Решая задачу вторым способом, мы рассуждали так:
а) стоимость ткани при постоянной цене зависит от количества метров ткани (то есть между стоимостью ткани и ее количеством существует зависимость);
б) эта зависимость имеет такое свойство: во сколько раз увеличивается количество метров ткани, во столько же раз увеличивается ее стоимость; если количество метров ткани уменьшается, то во столько же раз уменьшается ее стоимость.
Зависимость между величинами, имеющую такое свойство, называют прямой пропорцинальной зависимостью.
Зависимость двух величин называют прямой пропорциональной, если при увеличении (уменьшении) одной величины в несколько раз ко столько же раз увеличивается (уменьшается) другая величина.
В решении задачи речь идет о двух величинах, зависимость между которыми является прямой пропорциональной, или о двух прямо пропорциональных величинах: количестве метров ткани и их стоимости
3 м ткани стоят 60 три., или трем метрам ткани соответствует стоимость 60 руб. А 6 м ткани соответствует стоимость 120 руб. Из определения прямой пропорциональной зависимости следует, что отношение количества метров ткани 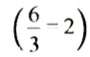
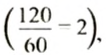
Итак, если две величины являются прямо пропорциональными, то отношение значений одной величины равно отношению соответствующих значений другой величины.
Решить задачи с помощью пропорций.
Пример:
Из 10 кг яблок получают 8 кг яблочного пюре. Сколько яблочного пюре получат из 44 кг яблок?
Решение:
Пусть из 44 кг яблок получат 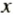
(Эту схему будем понимать так: 10 кг яблок соответствует 8 кг пюре, 44 кг яблок соответствует 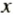
Масса яблок и соответствующая масса яблочного пюре являются прямо пропорциональными, так как во сколько раз больше мы возьмем яблок, во столько же раз больше получим яблочного пюре
По свойству прямо пропорциональных величин запишем пропорцию:
Откуда 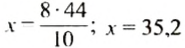
Пример:
Расстояние между Киевом и Тернополем равно 360 км. Каково расстояние между этими городами на карте с масштабом 1 : 5 000 000?
Решение:
Так как масштаб карты 1 :5 000 000, то 1 см на карте соответствует 5 000 000 см = 50 км на местности. Пусть расстояние между Киевом и Тернополем на карте равно 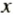
Расстояние на местности прямо пропорционально расстоянию на карте.
Поэтому 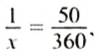
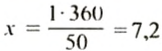
Пример:
Сплав состоит из меди, цинка и никеля, массы которых относятся как 13:3:4. Найти массу сплава, если для его изготовления использовали 1,8 кг цинка. (Отношение 13:3:4 означает, что в сплаве на медь приходится 13 частей, на цинк — 3 таких же по массе части на никель — 4 части.)
Решение:
Сплав состоит из 13 + 3 + 4 = 20 частей, из которых на цинк приходится 3 части. Пусть масса сплава равна 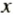
При постоянной массе части количество частей и их масса прямо пропорциональны.
Поэтому 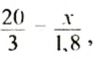
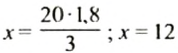
Процентное отношение
Отношение чисел или величин можно выражать в процентах, для этого отношение нужно умножить на 100%. Например, 3 : 5 = 0,6 = 0,6 • 100% = 60% Говорят, что число 3 составляет 60% от числа 5, или что процентное отношение чисел 3 и 5 равно 60%.
Решение:
Найдем процентное отношение чисел 15 и 10:
15 : 10= 1,5 = 1,5 • 100%= 150%.
Итак, число 15 составляет 150% от числа 10.
Оператор компьютерного набора в течение рабочего дня планировал набрать на компьютере 30 страниц текста, а набрал только 27. На сколько процентов оператор выполнил задание?
Задание, то есть 30 страниц, является тем числом, с которым нужно сравнить число 27, поэтому нужно найти процентное отношение чисел 27 и 30. Имеем:
27 : 30 = 0,9 • 100% = 90%.
Итак, оператор выполнил задание на 90%.
Пример:
Вместо плановых 80 деталей рабочий изготовил 90 деталей Сколько процентов плана выполнил рабочий?
Решение:
Чтобы ответить на вопрос задачи, нужно найти, сколько процентов составляет 90 от 80. Для этого нужно найти отношение чисел 90 и 80 и выразить его в процентах:
Итак, рабочий выполнил 112,5% плана.
Пример:
В 10%-й раствор соли массой 450 г досыпали 30 г соли. Найти процентное содержание соли в новом растворе.
Решение:
1. 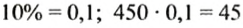
2. 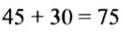
3. 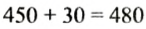
4. 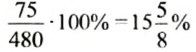
Ответ.
Процентные расчеты
Мы решали задачи на проценты путем сведения их к основным задачам на дроби. Эти задачи можно решать и с помощью пропорций. Рассмотрим такой способ решения задач на проценты.
Пусть в школе 50 шестиклассников. Тогда:
Какая существует зависимость между числом процентов и количеством учеников соответствующим этим процентам?
Во сколько раз увеличивается число процентов, во столько же раз увеличивается количество учеников, соответствующее этим процентам.
Итак, число процентов некоторой величины прямо пропорционально значению величины, которое соответствует этим процентам.
Помним, что 100% некоторой величины — это сама величина.
Пример:
Из свежих слив получают 21% сушеных. Сколько сушеных слив можно получить из 80 кг свежих?
Решение:
Пусть из 80 кг свежих слив можно получить 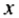
Какова зависимость между массой сушеных слив и числом процентов, которые составляет эта масса от массы свежих слив?
Масса сушеных слив прямо пропорциональна количеству процентов, которое составляет эта масса от массы свежих слив, поэтому:
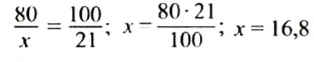
Пример:
Банк дал предпринимателю кредит 10 000 руб. со ставкой 7% годовых. Какую сумму должен вернуть предприниматель банку через пол года?
Решение:
Если процентная ставка за год составляет 7%, то за полгода будет насчитано 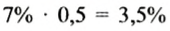
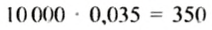
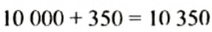
Ответ. 10 350 руб.
Пример:
Фермер в прошлом году собрал в среднем по 30 ц зерновых с 1 га, а в нынешнем году — по 32 ц. На сколько процентов увеличилась урожайность зерновых в нынешнем году по сравнению с прошлым годом?
Решение:
Сначала найдем, на сколько центнеров больше зерновых собрал фермер в нынешнем году: 32-30 = 2 (ц). Теперь вычислим, сколько процентов составляет найденная разность от урожая прошлого года. Поскольку сравниваем с урожайностью прошлого года, то 30 ц составляет 100%, а 2 ц —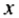
Итак, урожайность возросла на
Ответ.
Чтобы узнать, на сколько процентов увеличилась или уменьшилась данная величина, нужно найти:
- на сколько единиц увеличилась или уменьшилась данная величина;
- сколько процентов составляет полученная разность от начального значения величины.
Пример:
В процессе перегонки нефти из нее получают 30% керосина. Сколько нужно нефти, чтобы получить 9 т керосина?
Решение:
Масса нефти составляет 100%, а масса керосина — 30%. Пусть для того, чтобы получить 9 т керосина, нужно переработать 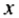
Составляем пропорцию: 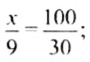
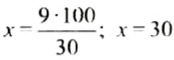
Пример:
Сколько процентов составляет число 24 от числа 30?
Решение:
Так как число 24 сравниваем с числом 30, то число 30 составляет 100%. Пусть число 24 составляет 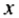
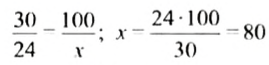
Пример:
Цену товара, который стоил 200 руб., снизили на 10%. На сколько процентов нужно повысить новую цену, чтобы получить начальную?
Решение:
Начальная цена (200 руб.) составляет 100%, а сниженная цена составляет 100% — 10% = 90% от начальной. Пусть цена после снижения равна 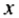
200 руб. — 100%; 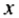
Чтобы найти, на сколько процентов нужно повысить новую цену, чтобы получить начальную, сравним с новой ценой (180 руб.) старую цену. Новая цена составляет 100%. Пусть начальная цена (200 руб.) составляет 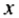
Итак, новую цену нужно повысить на
Ответ.
Окружность. Длина окружности
Представление об окружности дают руль автомобиля, обруч, кольцо и т. п. Нарисуем окружность. Для этого обозначим на плоскости некоторую точку О. Возьмем циркуль, поставим его ножку с иглой в точку О и раствором в 3 см другой ножкой циркуля опишем фигуру. Получим окружность с центром в точке О. Все точки окружности расположены на расстоянии 3 см от центра.
Соединим центр окружности с произвольной точкой А этой окружности отрезком (рис. 5). Отрезок OA, а также его длину называют радиусом окружности. Радиус построенной окружности равен 3 см. Отрезок, соединяющий две точки окружности и проходящий через ее центр, а также длину этого отрезка называют диаметром. Диаметр окружности в два раза длиннее радиуса этой окружности.
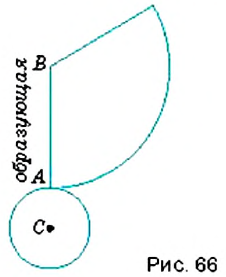
Две точки А и В, лежащие на окружности (рис. 6), разбивают ее на две части. Каждую из этих частей называют дугой окружности. Точки А и В — концы этих дуг. Если точки А и В являются концами диаметра, то они разбивают окружность на две равных части, каждую из которых называют полуокружностью.
Практическая работа
Тема работы. Длина окружности.
Оборудование. Циркуль, линейка, нитка
Ход работы.
1. Строим окружность, радиус которой равен 2 см
2. Накладываем на окружность нитку (см. рис. 7).
3. Ставим ручкой отметку на нитке в той точке, в которой нитка совпадает со своим началом.
4. Расправляем нитку и измеряем ее длину до отметки. Эта длина равна длине окружности.
5. Диаметр окружности d равен 4 см: d = 4 см; длина окружности С равна:
6. Находим отношение
Оказывается, что для всех окружностей отношение длины окружности к длине ее диаметра является одним и тем же числом. Это число обозначают греческой буквой 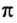
Итак, 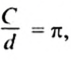
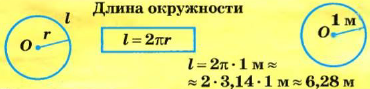
Длина окружности равна произведению числа 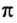
Так как диаметр окружности равен двум радиусам, то длина окружности радиуса 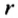
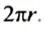
Далее для расчетов мы, как правило, будем округлять число 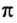
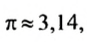
Пример:
Начертить окружность, радиус которой 2 см. Где лежит точка, находящаяся от центра на расстоянии 1 см; 2 см; 3 см? Чему равен диаметр окружности?
Решение:
Точка А, расстояние от которой до центра 2 см (рис. 9). принадлежит окружности.
Точка В, расстояние от которой до центра 1 см (рис. 9), лежит внутри окружности.
Точка С, расстояние от которой до центра 3 см (рис. 9), лежит вне окружности.
Диаметр окружности: 2 • 2 = 4 (см).
Пример:
Найти длину окружности, радиус которой 1,5 см.
Решение:
Круг. Площадь круга
Каждая окружность разбивает плоскость, на которой она начерчена, на две части — внутреннюю и внешнюю. Точки окружности и все внутренние точки образуют круг (рис. 12). Центр, радиус и диаметр окружности называют соответственно центром, радиусом и диаметром этого круга. 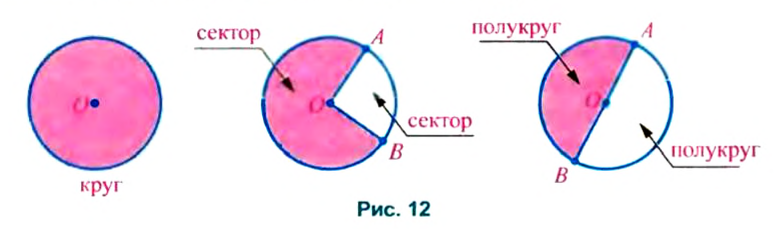
Практическая робота
Тема работы. Площадь круга.
Оборудование. Циркуль, линейка, листок бумаги в клетку.
Ход работы
1. На листке бумаги в клетку строим окружность, радиус которой 4 см (8 клеток).
2. Обводим внешний контур тех клеток, которые почти полностью принадлежат кругу (см. рис. 13).
3. Считаем количество клеток внутри контура.
4. Считаем количество клеток вне контура, которые частично принадлежат кругу, и полученное число делим на 2 (в среднем части двух неполных клеток дают одну целую).
5. Прибавляем к числу клеток, полностью принадлежащих кругу, число, полученное в п. 4.
6. Так как площадь 4 клеток равна 1 см 2 , то, чтобы выразить площадь круга в квадратных сантиметрах, делим число, полученное в п. 5, на 4. Получаем приближенное значение площади:
7. Находим квадрат радиуса круга:
8. Находим отношение
В старших классах будет доказано, что 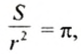
Получена формула для площади 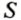
Пример:
Найти площадь круга, радиус которого равен 1,5 см.
Решение:
Столбчатые и круговые диаграммы
Для наглядной иллюстрации числовых значений величин используют диаграммы. Диаграмма — это символический рисунок, который наглядно отражает соотношения между значениями величин. Чаще всего используют столбчатые и круговые диаграммы.
Рассмотрим пример. Ученик шестого класса в октябре записал в дневнике погоды: 17.10 — облачно, 18.10 — облачно, 19.10 — солнечно, 20.10—дождь, 21.10 — дождь, 22.10 — облачно, 23.10 — солнечно, 24.10 — солнечно, 25.10 — облачно, 26.10 — дождь, 27.10 — дождь, 28.10 — дождь, 29.10 — облачно, 30.10 — солнечно, 31.10 — облачно.
Чтобы охарактеризовать погоду во второй половине октября, он подсчитал, сколько было солнечных дней, облачных дней, сколько дней шел дождь и получил такие данные: солнечных дней — 4; облачных дней — 6; дней, когда шел дождь, — 5.
Наглядно охарактеризовать погоду во второй половине октября можно так. Построим прямой угол АОВ, на луче OA будем записывать погоду, а на луче ОВ, выбрав единицу измерения (1 см), будем обозначать количество дней. Построим три столбика (прямоугольника) (рис. 18).
Высота первого столбика, указывающего, сколько было солнечных дней. — 4 см; высота второго, указывающего количество облачных дней. — 6 см, высота третьего, указывающего, сколько дней шел дождь, — 5 см.
Полученный рисунок называют столбчатой диаграммой.
Строя столбчатые диаграммы, можно выбирать произвольную ширину столбца и произвольные расстояния между ними. Но все столбики одной диаграммы должны быть одинаковой ширины и располагаться на одинаковом расстоянии друг от друга.
Следующую диаграмму (рис. 19) называют круговой. На ней показано соотношение между площадями поверхностей суши и Мирового океана на Земле.
Пример:
После сбора урожая зерновых культур выяснилось, что 50% всего урожая составляет пшеница, 15% — рожь, 10% — овес и 25% — ячмень. Построить столбчатую и круговую диаграммы распределения урожая зерновых по вилам культур.
Решение:
Столбчатая диаграмма распределения урожая изображена на рисунке 20, а круговая — на рисунке 21.
Опишем построение круговой диаграммы. Так как на 100% урожая приходится весь круг, то на урожай пшеницы (50%) приходится полукруг, а на урожай ячменя (25%) — четверть круга. Чтобы построить сектор, которому соответствует урожай ржи (15% всего урожая), будем рассуждать так. В секторе АОС, который составляет четверть круга, угол АОС равен 90°. Итак, на четверть, или на 25%, круга приходится сектор с углом 90°. Поэтому па 1% круга приходится сектор с углом 90° : 25 = 3,6°, а на 15% круга — сектор с углом 3,6° -15 = 54°. Построив с помощью транспортира угол АОВ, равный 54°, получили сектор АОВ, соответствующий урожаю ржи. Тогда остальная часть круга сектор ВОС соответствует урожаю овса.
Памятка:
— отношение;
число 90 в три раза больше от числа 30.
— отношение;
число 30 составляет
от числа 90.
— пропорция.
— основное свойство пропорции.
- Из сахарного тростника получают 9% сахара. Сколько сахара получат из 40 т сахарного тростника?
— длина окружности,
— ее радиус,
— площадь круга,
— его радиус.
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Отношения и пропорции
Отношение и его свойства
Вам, наверное, приходилось слышать фразы: «Шанс победить в игре — 50 на 50», «Для приготовления гречневой каши крупу и воду нужно взять в отношении 1 к 2», «Прибыль разделили, как 3 к 2». Каждая из этих фраз подводит к сравнению двух чисел: 50 и 50, 1 и 2, 3 и 2. Для этого нужно составить выражение, являющееся частным данных чисел, и вычислить его значение». Итак, из первой фразы получим выражение 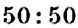
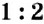
Определение:
Выражение, являющееся частным чисел 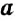
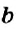
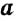
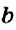

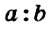
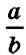
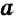
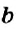
Числа 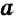
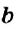
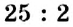
Отношение показывает, какие числа сравнивают. Значение отношения показывает, во сколько раз первое число больше второго, или какую часть второго числа составляет первое число. Например, значение отношения 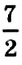
А значение отношения 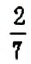
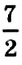
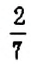
Обратите внимание:
- — если
, то значение отношения
к
показывает, во сколько раз число
больше числа
;
- — если
, то значение отношения
к
показывает, какую часть числа
составляет число
.
Для вычисления значения отношения используют все свойства деления.
Основное свойство отношения
Значение отношения не изменится, если его члены умножить или разделить на одно и то же число, отличное от нуля:
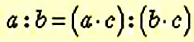
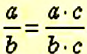
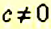
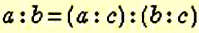
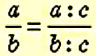
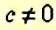
Для решения задач составляют отношения и находят их значения как для одноимённых величин, так и для величин с разными наименованиями.
Пример:
Длина самой крупной рыбы — луны-рыбы — составляет около 3 м, а длина самой мелкой рыбы — гоби — около 16 мм. Сравните длины этих рыб.
Решение:
1. Можно найти, во сколько раз длина луны-рыбы больше длины рыбы гоби. Для этого составим отношение длины большей рыбы к длине меньшей, выразим эти величины в одних наименованиях и найдём значение отношения:
2. Можно найти, какую часть длины луны-рыбы составляет длина рыбы гоби. Для этого составим обратное отношение длин и найдём его значение:
Обратите внимание:
значение отношения одноимённых величин является числом без наименования.
Пример:
Найдите скорость гепарда, если за 2 с он преодолевает около 55 м.
Решение:
Для нахождения скорости движения нужно составить отношение расстояния ко времени движения и вычислить его значение:
Обратите внимание:
значение отношения разноимённых величин является новой величиной, наименование которой отличается от наименований данных величин.
Пентаграмма (рис. 11) всегда привлекала внимание совершенством формы. Особенность данной фигуры состоит в том, что отношения отрезков, из которых она состоит, имеют равные значения:
Древнегреческий математик Пифагор (570—490 гг. до н.э.) и его ученики избрали пентаграмму символом своего союза. В наши дни пятиконечная звезда пентаграммы украшает флаги и гербы многих стран.
Пропорция и её свойства
Вы знаете, что два выражения с равными значениями можно приравнять. Например, можно приравнять отношения 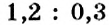
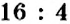
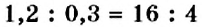
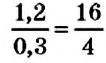
Определение:
Пропорцией называется равенство двух отношений.
Обратите внимание:
пропорция утверждает, что отношения в левой и правой её частях имеют равные значения.

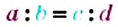
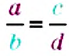
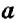
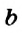
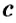
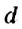
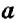
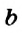
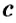
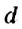
Числа 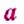
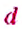
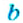

Обратите внимание:
пропорции составляют только для чисел, отличных от нуля.
Вычислим произведения крайних и средних членов пропорции 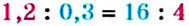
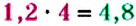

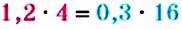
Основное свойство пропорции
Произведение крайних членов пропорции равно произведению её средних членов:
если
И наоборот: если 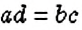
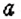
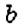
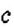
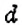
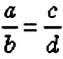
Пример:
Является ли равенство 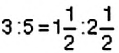
Решение:
Способ 1. Применим определение пропорции: 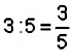
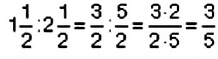
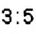
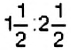
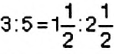
Способ 2. Проверим, выполняется ли основное свойство пропорции 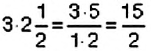
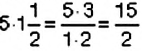
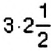
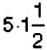
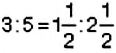
В пропорции 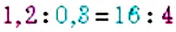
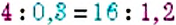
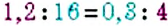
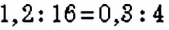
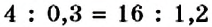
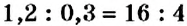
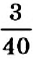
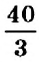
В пропорциях 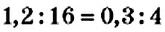
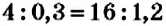
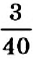
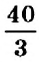
Пример:
Изменится ли пропорциональное соотношение чисел, если средние члены пропорции поменять местами с соответствующими крайними членами? Нет. В самом деле, если в каждом отношении пропорции 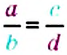
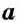
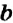
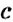
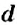
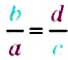
Опираясь на основное свойство пропорции, можно находить неизвестный член пропорции.
Пример:
Найдите неизвестный член пропорции: 1) 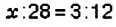
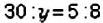
Решение:
1. Неизвестным является крайний член пропорции 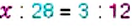
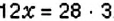
Отсюда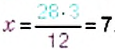
2. Неизвестным является средний член пропорции 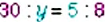
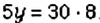
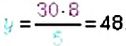
Правила нахождения неизвестного члена пропорции
Правила нахождения неизвестного члена пропорции
- Чтобы найти неизвестный крайний член пропорции, нужно произведение её средних членов разделить на известный крайний член пропорции.
- Чтобы найти неизвестный средний член пропорции, нужно произведение её крайних членов разделить на известный средний член пропорции.
Термин «пропорция» происходит от латинского proportio — «соотношение».
Золотым сечением называют деление отрезка с на две неравные части 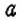
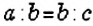
Считают, что понятие золотого сечения было известно в Древнем Египте. И в самом деле, пропорции пирамиды Хеопса, храмов. барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют о том. что при их создании египетские мастера пользовались отношением золотого сечения.
Прямая и обратная пропорциональные зависимости
С помощью пропорций можно решать задачи.
Вы знаете, например, что стоимость товара зависит от его количества: чем большее количество товара покупают, тем большей будет его стоимость. Такие величины называют прямо пропорциональными.
Определение:
Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной величины в несколько раз другая величина увеличивается (уменьшается) в такое же количество раз.
Пример:
За 2 кг конфет заплатили 72 грн. Сколько будут стоить 4.5 кг этих конфет?
Решение:
Обратите внимание:
если две величины прямо пропорциональны, то пропорцию образуют отношения соответствующих значений этих величин.
На практике, кроме прямой пропорциональной зависимости величин, встречается и обратная пропорциональная зависимость. Например, по пути в школу, когда времени маловато, вы увеличиваете скорость своего движения, чтобы не опоздать на урок. Итак, скорость вашего движения зависит от времени движения: чем меньше время движения, тем большей будет ваша скорость. Такие величины называют обратно пропорциональными.
Определение:
Две величины называются обратно пропорциональными, если при увеличении (уменьшении) одной величины в несколько раз другая величина уменьшается (увеличивается) в то же количество раз.
Пример:
Автомобиль, двигаясь со скоростью 90 км/ч. проехал расстояние от Черкасс до Киева за 2 ч. С какой скоростью он двигался в обратном направлении, если расстояние от Киева до Черкасс он преодолел за 2.5 ч?
Решение:
Обратите внимание:
если две величины обратно пропорциональны, то пропорцию образуют взаимно обратные отношения соответствующих значений этих величин.
Пример:
Всегда ли две величины являются прямо пропорциональными или обратно пропорциональными? Порассуждаем. Например, во время болезни температура ребёнка может то возрастать, то понижаться на протяжении нескольких дней. И здесь нет зависимости, следовательно, не может быть и пропорциональности. А вот рост ребёнка постоянно увеличивается с увеличением его возраста. Значит, существует зависимость между величинами и есть основания анализировать, пропорциональны ли данные величины. Понятно, что пропорциональной зависимости здесь нет, поэтому выяснять, как именно пропорциональны эти величины — прямо или обратно, — не надо. Если же две величины пропорциональны, то возможны лишь два варианта, взаимно исключающие друг друга, — или прямая пропорциональность, или обратная пропорциональность.
С историей золотого сечения косвенным образом связано имя итальянского математика и монаха Леонардо из Пизы (1180-1240 гг.), более известного как Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г. вышла в свет его математическая работа «Книга об абаках» (счётные доски), в которой были собраны все известные к тому времени задачи. Одна из задач была такой: «Сколько пар кроликов за один год от одной пары родится?». Размышляя на эту тему, Фибоначчи выстроил такой ряд чисел:
Сегодня эта последовательность чисел известна как ряд Фибоначчи. Особенность данной последовательности чисел заключается в том, что каждый её член, начиная с третьего, равен сумме двух предыдущих:
и т.д, а отношение соседних чисел ряда приближается к отношению золотого сечения. Например, 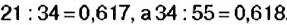
Деление числа в данном отношении
Пропорциональное деление
На практике часто встречаются задачи с требованием разделить некоторую величину в заданном отношении: распределение прибылей, приготовление разных смесей или блюд и т.п. Чтобы решить такие задачи, нужно выполнить пропорциональное деление данной величины.
На рисунке 16 вы видите отрезок 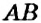
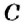
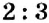
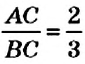
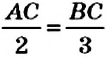
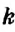
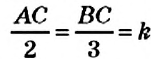
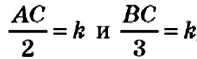
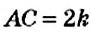
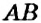
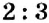
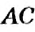
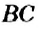
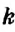
Определение:
Число, равное значению отношений пропорции, называется коэффициентом пропорциональности.

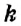
Иногда приходится пропорционально делить величину более чем на две части. И тут снова на помощь приходит коэффициент пропорциональности.
Пример:
Разделите число 60 в отношении 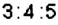
Решение:
Пусть 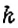
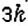
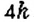
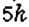
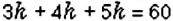
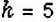
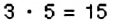
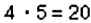
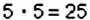
Масштаб
Для изображения на бумаге предметов окружающего мира нужно менять их реальные размеры: большие предметы приходится уменьшать, а маленькие — наоборот, увеличивать. Но для того, чтобы чертёж или план давали представление о предметах, необходимо изменять их размеры пропорционально. Для этого используют масштаб изображения.
Чаще всего масштаб применяют для создания географических карт.
Определение:
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называется масштабом карты.

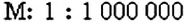
Пример:
Расстояние между Черкассами и Харьковом на карте равно 4.1 см. Найдите расстояние между этим и городам и на местности, если масштаб карты 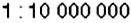
Решение:
На карте: 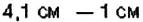
На местности: 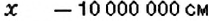
Тогда отношение длины отрезка на карте к длине отрезка на местности: 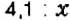
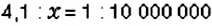
Отсюда 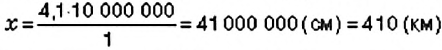
Ответ: расстояние от Черкасс до Харькова — 410 км.
Пример:
Как записать масштаб изображения, если на нём нужно увеличить размеры реального предмета например в 1000 раз. В этом случае масштаб записывают наоборот: 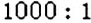
1. Слово «коэффициент» происходит от латинского Coefficiens, состоящего из двух слов: Со — «вместе» и efficiens — «вырабатывающий». Обозначает множитель, который обычно выражается числом. Термин ввёл Ф. Виет.
2. Слово «масштаб» происходит от немецкого 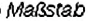
Окружность и круг. Круговой сектор
Из всех замкнутых кривых линий на плоскости самой совершенной считается окружность. Если закрепить один конец отрезка в какой-либо точке, а затем поворачивать отрезок, то другой его конец будет двигаться именно по окружности. Поэтому окружности изображают с помощью циркуля (рис. 25).
Определение:
Окружность — это фигура, все точки которой находятся на плоскости на одинаковом расстоянии от одной точки, называемой центром окружности.
На рисунке 26 вы видите окружность с центром в точке 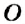
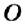
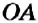
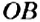
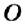
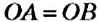

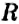
Обратите внимание:
все радиусы окружности равны между собой.
Проведём радиусы 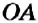
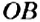
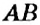
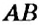
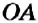
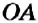
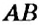
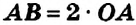

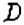
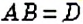
Формула диаметра окружности
Диаметр окружности равен удвоенному радиусу:
Пример:
Найдите радиус окружности с диаметром 8 см.
Решение:
Диаметр окружности вдвое длиннее радиуса. Следовательно,
Пример:
Можно ли найти длину окружности? Да, поскольку окружность — это линия. Но линейкой окружность не измерить. Проведём опыт. Возьмём стакан, поставим его на лист бумаги и обведём карандашом (рис. 28). Получили окружность. Если обвязать стакан ниткой, а затем распрямить её, то длина нитки будет равна длине изображённой окружности.


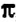
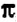
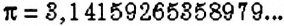
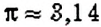
Формула длины окружности
Длина окружности равна удвоенному произведению числах 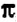
Пример:
Найдите длину окружности с диаметром 10 см.
Решение:
Способ 1. Диаметр окружности вдвое длиннее радиуса. Следовательно, 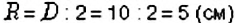
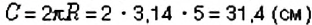
Способ 2. Поскольку 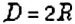
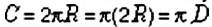
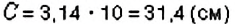
Обратите внимание:
поскольку 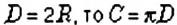
Окружность делит плоскость на две части — внутреннюю и внешнюю (рис. 29). О внутренней части говорят, что окружность ограничивает эту часть плоскости. Окружность вместе с частью плоскости, которую она ограничивает, образует известную вам фигуру — круг (рис. 30). Центр окружности считают и центром круга, радиус и диаметр окружности — радиусом и диаметром круга. В отличие от окружности, центр круга является точкой круга.
Формула площади круга
Площадь круга равна произведению числа к и квадрата радиуса:
Пример:
Найдите площадь круга с диаметром 8 см.
Решение:
Диаметр круга вдвое длиннее радиуса. Поэтому: 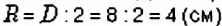
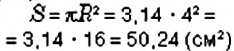
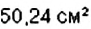
Если в круге провести два радиуса 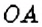
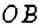
На рисунке 32 показан сектор 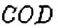
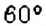
Диаметр 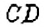
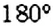
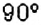
Обратите внимание:
- — у равных секторов — равные углы.
- — сумма углов всех секторов, на которые разделён круг, равна
.
Пример:
Круг разделён на 3 равных сектора. Найдите угол сектора.
Решение:
Сумма углов всех данных секторов равна 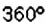
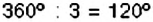
Пример:
Круг разделён на 3 сектора з углами 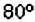
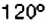
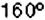
Решение:
Каждый из данных секторов составляет такую часть круга, какую его угол составляет от 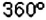
1. Самые первые известные записи приближений числа 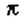
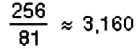
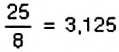
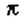
2. Общепринятое обозначение к впервые применил в своих работах Вильям Джонс в 1706 г.. взяв первую букву греческих слов 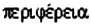
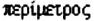
Диаграммы
Для наглядного изображения частей целого или соотношения величин используют диаграммы.
Они могут быть круговыми (рис. 39) или столбчатыми (рис. 40).
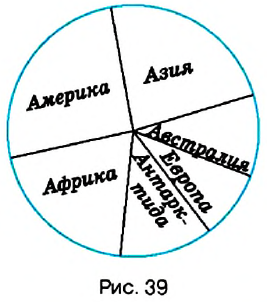
Для построения круговой диаграммы целое изображают кругом, а отдельные части целого — секторами круга. Например, на рисунке 39 круговая диаграмма показывает соотношение площадей частей света.
По этой диаграмме можно ответить, например, на такие вопросы.
- Сколько частей света на нашей планете?
- Какая часть света самая большая?
- Какая часть света самая маленькая?
- Какая из двух частей света больше: Антарктида или Австралия?
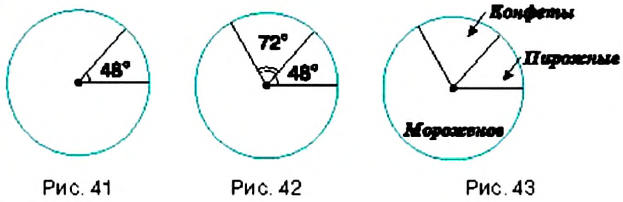
Пример:
Среди учеников класса провели опрос, в результате которого оказалось, что 20 шестиклассников больше всего любят мороженое, 6 учеников класса — конфеты, а остальные 4 ученика — предпочитают пирожные. Постройте круговую диаграмму любимых лакомств учеников 6-А класса.
Решение:
Для построения круговой диаграммы нужно круг разделить на три сектора пропорционально количеству лакомок, то есть выполнить пропорциональное деление 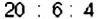
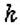
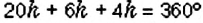
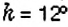
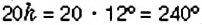
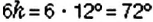
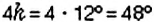
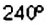
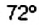
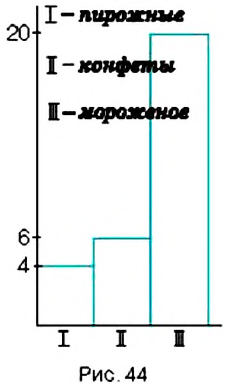
Для построения столбчатой диаграммы сравниваемые величины изображают в виде столбиков, высота которых либо равна данным величинам, либо пропорциональна им. Например, на рисунке 44 столбчатая диаграмма показывает соотношение любимых лакомств учеников 6-А класса. Для её построения изобразили три столбика, высота которых пропорциональна количеству учеников, предпочитающих мороженое, конфеты и пирожные: 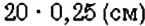
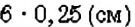
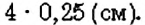
Слово «диаграмма» происходит от греческого diagramma, что означает изображение, чертёж.
Благодаря наглядности диаграммы часто используют в презентациях. Например, на уроках природоведения, пользуясь данными календаря погоды, вы можете строить диаграммы выпадения осадков и анализировать их.
Цилиндр. Конус. Шар
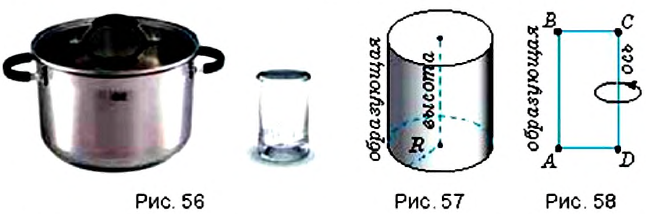
В 5 классе вы уже ознакомились с пространственными фигурами: прямоугольным параллелепипедом и кубом. Посмотрите на рисунок 56. Вы видите разнообразные предметы, используемые в быту. Все они имеют одну и ту же форму — цилиндра (рис. 57).
Цилиндр получим при вращении прямоугольника 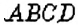
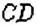
Эту сторону прямоугольника считают осью цилиндра, а противоположную ей сторону 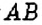
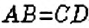
При вращении образующая цилиндра описывает поверхность, которую называют боковой поверхностью цилиндра. Полную поверхность цилиндра составляют его боковая поверхность и два круга оснований.
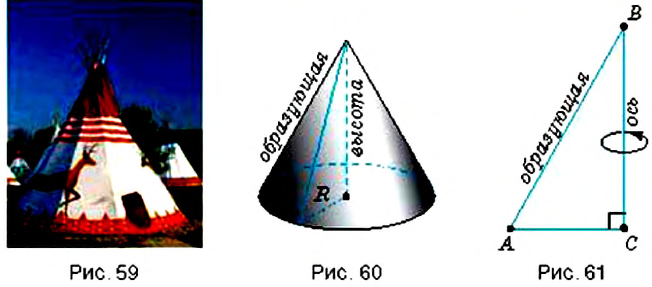
На рисунке 59 вы видите индейское жилище 
Конус можно получить, вращая прямоугольный треугольник 
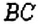
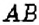
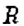
При вращении, образующая конуса описывает поверхность — боковую поверхность конуса. Полную поверхность конуса составляют его боковая поверхность и круг основания.
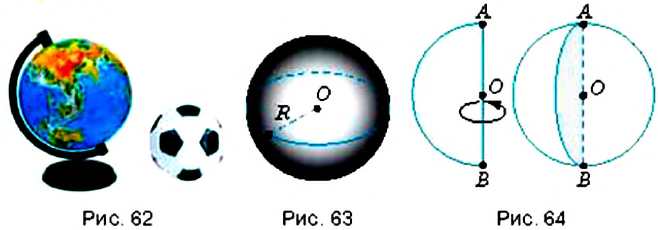
На рисунке 62 вы видите предметы, имеющие форму шара (рис. 63).
Шар можно получить, вращая круг вокруг его диаметра 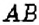
Поверхность шара имеет особое название — сфера. Цилиндр, конус и шар называют телами вращения т. к. их можна получить при вращении прямоугольника, прямоугольного треугольника и круга. Больше об этих фигурах вы узнаете в курсе геометрии.
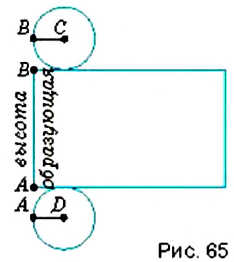
Бумажную модель пространственной фигуры делают из её развёртки. Чтобы получить развёртку цилиндра (рис. 65), отделяют основание, а боковую поверхность разрезают вдоль образующей и разворачивают на плоскости. Боковая поверхность цилиндра разворачивается в прямоугольник, одна сторона которого равна образующей, а вторая — имеет длину окружности основания. Развёртка цилиндра состоит из этого прямоугольника и двух кругов оснований. Аналогично получают развёртку конуса (рис. 66). Его боковая поверхность разворачивается в сектор. Развёртка конуса состоит из этого сектора и круга основания конуса.
Для шара изготовить традиционную развёртку невозможно.
Процентные расчёты
В 5 классе вы узнали, что такое процент и как решать задачи на нахождение процента от числа и числа по его проценту. Рассмотрим, как решать такие задачи с помощью пропорций и познакомимся с другими видами задач на процентные расчёты.
Нахождение процента от числа
Пример:
Мама Малыша испекла 25 ватрушек. Карлсон съел 40 % ватрушек. Сколько ватрушек съел Карлсон?
Решение:
Обратите внимание:
чтобы найти число 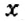
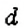
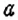
если 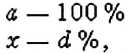
Нахождение числа по его проценту
Пример:
В 6-А классе высокий уровень учебных достижений имеют 6 учеников, что составляет 20% учеников класса Сколько учеников учится в 6-А классе?
Решение:
По условию задачи, 6 отличников — это 20 % учащихся класса. В задаче нужно узнать, сколько учащихся составляют 100 %. Составим краткую запись данных задачи.
Учащихся в классе:
Отличников:
Пусть 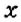
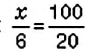
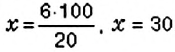
Обратите внимание:
чтобы найти число 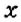
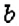
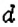
если 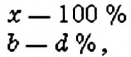
Нахождение процентного отношения двух чисел
Пример:
Из 30 учеников 6-Б класса в спортивных соревнованиях приняли участие 18 учеников. Сколько процентов учащихся класса приняли участие в спортивных соревнованиях?
Решение:
По условию задачи, в классе 30 учеников, что составляет 100 %. В задаче нужно узнать, сколько процентов составляют 18 учеников. Составим краткую запись данных задачи.
В классе:
Приняли участие:
Пусть 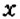
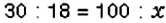
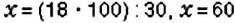
Обратите внимание:
чтобы найти процентное отношение двух чисел а и &. составляют пропорцию:
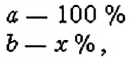
Пример:
Верно ли, что процентное отношение чисел 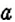
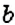
Рассмотрим более сложные задачи.
Нахождение изменения процента по изменению числа
Пример:
Пчёлы за день принесли в улей 2 кг мёда. На следующий день они работали лучше и собрали 2.5 кг меда. На сколько процентов больше мёда собрали пчёлы во второй день?
Решение:
По условию задачи, за день пчёлы принесли в улей 2 кг меда, что составляет 100 %. В задаче нужно выяснить, на сколько процентов 2,5 кг мёда больше, чем 2 кг. Составим краткую запись данных задачи.
I день:
II день:
Пусть 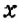
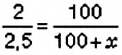
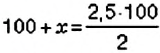
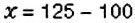
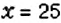
Обратите внимание:
чтобы найти, на сколько изменится процент 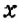
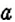
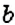
если 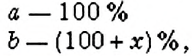
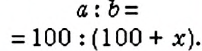
Пример:
Можно ли аналогично решать задачи на уменьшение числа? Да. В таком случае нужно составить пропорцию
Нахождение числа по его процентному изменению
Пример:
В 10 лет Ванин рост составлял 130 см. Каким был рост Вани в 9 лет, если за год он подрос на 4 %?
Решение:
По условию задачи, рост Вани в 10 лет составлял 130 см, что на 4 % больше, чем в 9 лет Значит, росту Вани в 9 лет соответствует 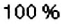
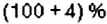
Рост в 9 лет: 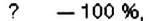
Рост в 10 лет:
Пусть 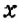
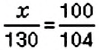
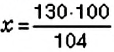
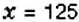
Пример:
Можно ли рост Вани в 10 лет принять за 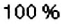
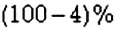
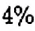
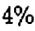
Обратите внимание:
чтобы найти число 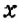
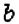
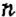
если 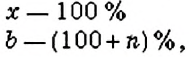
Нахождение процентного отношения двух чисел по изменению числа
Пример:
В первый день Маша прочитала 20 страниц книжки, а во второй — на 5 страниц больше. Сколько в процентах прочитала Маша во второй день по сравнению с первым днём?
Решение:
По условию задачи, в первый день Маша прочитала 20 страниц, что составляет 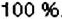
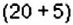
I день:
II день:
Пусть 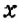
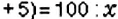
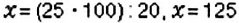
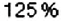
Обратите внимание:
чтобы найти процентное отношение двух чисел 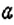
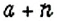
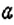
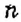
если 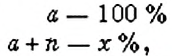
Пример:
Можно ли аналогично решать задачи на уменьшение числа? Да. В таком случае нужно составить пропорцию
В параграфе вы рассмотрели решение задач с помощью алгебраического способа. Но каждую из них можно решить и арифметически, к тому же не одним способом. Обратимся к задаче 1 данного параграфа.
Пример:
Мама Малыша испекла 25 ватрушек. Карлсон съел 40 % всех ватрушек. Сколько ватрушек съел Карлсон?
Решение:
Арифметический способ 1.
1) Сколько ватрушек составляет 1 %?
2) Сколько ватрушек составляют 40%?
Значит, Карлсон съел 10 ватрушек.
Арифметический способ 2.
1) Как выразить 40 % дробью?
2) Сколько ватрушек составляют 40 %?
Значит, Карлсон съел 10 ватрушек.
Вероятность случайного события
В повседневной жизни часто планируются разные события, о которых можно сказать, произойдут они или нет. Примером таких событий могут быть: празднование дня рождения, поход в школу, получение хорошей оценки, поездка с родителями за город и др.
Определение:
Событие, о котором можно сказать, что оно произойдёт или не произойдёт при определённых условиях, называется случайным событием, или (кратко) событием.

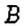
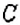
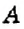
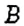
Математики считают, что любое случайное событие происходит (или не происходит) вследствие проведения некоторого эксперимента. Такой эксперимент называют случайным, или стохастическим. Он является испытанием. Условия проведения испытания являются неизменными. Возможные результаты испытания известны, но нельзя заранее знать, какой именно из них будет иметь место. Например, если мы будем подбрасывать монету один раз, то возможны два следствия: выпадет или «герб», или «цифра» (рис, 76), однако нельзя точно сказать, что именно выпадет. Поэтому подбрасывание монеты является испытанием, а появление «герба» или «цифры» — это события 
Пример:
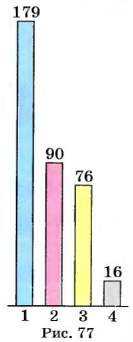
Сколько событий могут произойти вследствие подбрасывания игрального кубика (рис. 77)? У кубика шесть граней, поэтому событий может быть шесть — выпадает 1 очко, 2 очка, S очка, 4 очка, 5 очков или 6 очков.
Обратите внимание:
все возможные результаты испытания образуют совокупность событий, однако испытание завершается наступлением лишь одного из этих событий.
Например, в результате одного подбрасывания игрального кубика из шести возможных событий произойдёт лишь одно событие — или выпадет 1 очко, или 2 очка, или S очка, или 4 очка, или 5 очков, или 6 очков. Иначе говорят: «Появлению 1 очка благоприятствует только одно событие».
Событие, которое в результате испытания непременно должно произойти, называют достоверным. Например, событие 
Событие, которое вследствие данного испытания не может произойти, называют невозможным. Например, событие 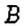
События называют несовместимыми, если наступление одного из них исключает наступление другого. Такие события не могут наступить одновременно. Например, событие 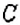
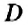
События называют равновозможными, если в результате испытания появление каждого из них одинаково возможно по сравнению с другими. Например, при подбрасывании игрального кубика все шесть событий (« появление 1 очка» и т.д.) являются равновозможными.
Вероятность события — это количественная характеристика возможности наступления этого события в ходе испытания.

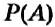
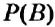
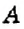
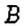
Для испытания, в котором все возможные события являются несовместными и равновозможными, вероятность события можно вычислить по формуле.
Определение:
Вероятностью события 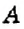
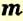
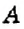
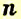
Пример:
Верно ли, что количество испытаний 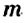
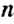
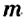
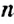
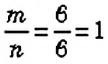
Обратите внимание:
вероятность события может принимать значения только от 0 до 1. Вероятность достоверного события равна 1. а вероятность невозможного события — 0.
Пример:
Из коробки, где находятся 3 чёрных и 5 белых шариков, достали наугад один шарик. Какова вероятность того, что шарик:
1) чёрный; 2) белый?
Решение:
1. Событие 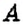
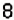
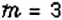
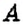
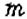
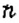
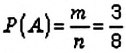
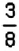
В рассмотренной задаче возможными были два события: событие 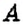
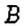
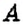
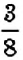
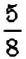
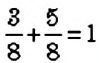
Определение:
Сумма вероятностей всех возможных событий испытания равна 1.
Пример:
Можно ли определить вероятность одного из двух возможных событий испытания, зная вероятность другого события? Да. Вероятность извлечения белого шарика в рассмотренной задаче можно было найти и по другому: 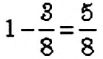
Пример:
Бросают два игральных кубика. Какова вероятность того, что в сумме выпадет 6 очков?
Решение:
Событие 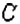
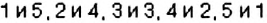
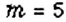
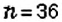
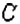
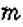
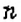
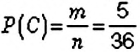
Стохастичность (от греческого 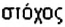
Теория вероятностей — это раздел математики, изучающий закономерности случайных событий. Как самостоятельная наука, теория вероятностей возникла в середине XVII века. Тогда были распространены азартные игры, то есть игры, в которых результат зависел от случая (игры с кубиками, игра в «орлянку», некоторые карточные игры). Они и способствовали анализу случайных событий. Считают, что история теории вероятностей начинается с работы Я. Бернулли (1654—1705) «Ars Conjectandi» («Искусство предположений»), опубликованной в 1713 году.
3. Обозначение 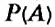
Видео:Длина окружности. Математика 6 класс.Скачать

Отношения и пропорции
В этом разделе речь идет о вещах, уже известных вам. Отношение — это частное, пропорция — равенство двух отношений. Например, 

- Основное свойство отношения.
- Вероятность случайного события.
- Пропорции.
- Процентное отношение.
- Пропорциональные величины.
- Окружность, круг, диаграммы.
Эти темы важны не только для математики и других наук, они часто используются в практической деятельности миллионов людей.
Отношения
Частное от деления одного числа на другое называют также отношением этих чисел. Записывают отношение с помощью двоеточия или черты дроби.
Примеры отношений:
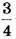
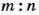
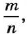
Основное свойство отношения Отношение двух чисел не изменится, если каждое из них умножить или разделить на одно и то же число, отличное от нуля.
Используя это свойство, отношения можно упрощать.
Оба члена отношения можно разделить на их общий делитель. Например, отношение 3000 : 5000 можно заменить равным ему отношением 3:5.
Отношение дробных чисел можно заменить отношением натуральных чисел.
Для этого надо данные дроби привести к общему знаменателю и отбросить его. Например,
Одним из примеров использования отношений является масштаб. Если, например, на географической карте указан масштаб 1 : 5 500 000, то это означает, что все расстояния на карте в 5 500 000 раз меньше соответствующих расстояний на земной поверхности. То есть одному сантиметру на карте соответствует 5 500 000 см (или 55 км) на местности.
Можно говорить не только об отношении чисел, а и об отношении значений величин. Если два значения какой-то величины выражены в одинаковых единицах измерения, то отношением этих значений называют отношение соответствующих чисел. Например, 3 м : 5 м = 3 : 5; 18 кг :9 кг =18: 9.
Но 2 м : 37 см = 200 см : 37 см = 200 : 37.
Иногда рассматривают и отношение значений разноименных величин. Например, если высота, площадь основания и объем прямоугольного параллелепипеда равны соответственно 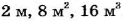
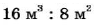
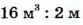
А если самолет пролетает расстояние 1400 км за 2 ч, то его скорость равна отношению расстояния ко времени: 1400 км : 2 ч = 700 км/ч.
Вообще, если какое-то тело движется равномерно, то его скорость — это отношение пройденного пути ко времени.
Со временем в физике вы будете рассматривать плотность вещества — отношение массы тела к объему, давление — отношение силы к площади и т. п.
Выполнение заданий:
Пример №43
Упростите отношение 400 : 600.
Решение:
ПОД (400, 600) = 200. Разделим каждый член данного отношения на 200. Имеем 400 : 600 = 2:3.
Пример №44
Замените отношение 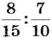
Решение:
Приведем заданные дроби к общему знаменателю 30.
Пример №45
Упростите отношение
Решение:
Вероятность случайного события
Отношение часто используют для определения вероятностей случайных событий.
Событие — это то, что совершается, происходит, случается. В математике чаще всего рассматривают события, какие еще не совершались, а только возможно произойдут. При этом стараются установить степень уверенности в том, что событие произойдет.
Примеры событий:
- подброшенная монета упадет гербом вверх (рис. 43);
- приобретенный лотерейный билет выиграет;
- после ночи наступит утро;
- игральная кость упадет кверху семеркой.
Последнее событие невозможно, поскольку на гранях кости семерки нет. Событие 3) достоверное, ведь после ночи всегда наступает утро. События 1) и 2) — случайные. Событие называется случайным, если оно может произойти или не произойти.
Степень уверенности в том, что случайное событие произойдет, можно характеризовать числом. Рассмотрим пример. При падении подброшенной игральной кости (рис. 44) может произойти 6 различных событий:
- событие А: выпадет 1 очко; событие Б: выпадет 2 очка;
- событие В: выпадет 3 очка; событие Г: выпадет 4 очка;
- событие Д: выпадет 5 очков; событие Е: выпадет 6 очков.
Все эти шесть событий имеют одинаковые шансы произойти (если кость правильной формы и изготовлена из одного материала). Такие события называют равновероятными. Дальше речь пойдет только о равновероятных событиях.
Вероятностью события называют отношение количества благоприятных для этого события результатов к количеству всех возможных результатов.
Вероятность события 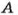
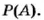
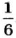
Вероятность достоверного события принимается за 1, а невозможного за 0. Вероятность можно выражать обыкновенной и десятичной дробью или процентами.
Задача 1. Какова вероятность того, что при падении игральной кости выпадет число очков, кратное 3?
Ре ш е н и е. Количество всех возможных событии равно 6. Среди чисел 1, 2, 3, 4, 5 и 6 только два (3 и 6) делятся на 3.
Поэтому вероятность равна 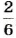
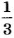
Задача 2. Найдите вероятность того, что ваш товарищ родился в воскресенье.
Решение. Всего в неделе 7 дней. Нас интересует событие: «Мой товарищ родился в воскресенье» (событие 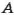
Поскольку воскресенье только 1 раз в неделю, то
Наведенная выше трактовка понятия вероятности верна только для равновероятных событий. Такое понимание вероятности называют классическим. Его чаще всего применяют при решении задач на азартные игры.
Намного важнее понятие статистической вероятности.
Для примера рассмотрим два похожих события: подброшенная монета упадет кверху гербом 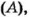
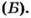
Пуговица с одной стороны не такая, как с другой (рис. 45). Поэтому два события (пуговица упадет петель-кой кверху или книзу) не равновероятные. Вероятность каждого из них можно определить только экспериментально. Такие вероятности (статистические) вы будете изучать в старших классах.
Пропорции
Отношения 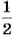
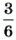
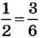
Пропорция — это равенство двух отношений.
В пропорции 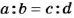
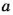
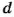
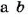
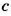
Произведение крайних членов каждой пропорции равно произведению ее средних членов.
Это — основное свойство пропорции. Его можно проиллюстрировать на примерах. Если 1 : 2 = 3 : 6, то 1 • 6 = 2 • 3; если 0,3 : 1 = 2,1 : 7, то 0,3 • 7 = 1 • 2,1. А можно и доказать.
Пусть дано произвольную пропорцию 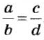
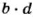
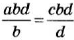
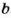
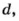
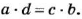
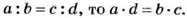
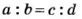
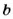
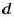
Любой член пропорции можно определить, если известны три других ее члена. Например, если 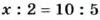
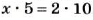
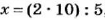
Чтобы найти неизвестный крайний член пропорции, достаточно произведение ее средних членов разделить на известный крайний. Чтобы найти неизвестный средний член пропорции, достаточно произведение ее крайних членов разделить на известный средний. Основное свойство пропорции используют при решении уравнений, имеющих вид пропорции.
Приведем примеры решения таких уравнений:
а)
б)
в)
Решение:
а)
б)
в)
Подобным способом можно решать, например, и уравнение 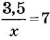
Отсюда
Если пропорция 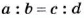
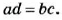
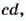
Отсюда 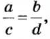
Следовательно, средние члены пропорции можно менять местами. Так же можно показать, что местами можно менять и крайние члены пропорции.
Например, поскольку 0,2 : 0,3 = 2 : 3, то верны также пропорции 0,2 : 2 = 0,3 : 3 и 3 : 0,3 = 2 : 0,2.
Выполнение заданий:
Пример №46
Составьте пропорцию из чисел 3, 4, 8 и 6.
Решение:
Поскольку 3 • 8 = 4 • 6, то числа 3 и 8 могут быть средними членами, а другие — крайними. Или наоборот. Поэтому верны пропорции:
4:3 = 8:6, 4:8 = 3:6, 8:4 = 6:3, 3:4 = 6:8.
Пример №47
Решите уравнение
Решение:
Поскольку произведение средних членов пропорции равно произведению крайних, то 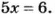
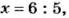
Процентное отношение
Один процент — это одна сотая часть.
1 % =0,01; 50% =0,5;
100 %=1; 200% =2.
Если отношение двух чисел выражают в процентах, то его называют процентным отношением.
Например, отношение 2 к 5 равно 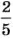
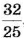
Существуют задачи, в которых требуется найти, сколько процентов составляет одно число относительно другого, или одно значение величины относительно другого. Их называют задачами на нахождение процентного отношения.
Задача. Возле школы растет 20 деревьев, из них 8 — липы. Сколько процентов этих деревьев составляют липы?
Решение. Отношение лип ко всем деревьям возле школы равно 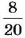
Учитывая сказанное выше и два известных вам вида задач на проценты с 5-го класса, можно подвести итоги.
Существует три основных вида задач на проценты:
- (1) нахождение процентов от числа;
- (2) нахождение числа по процентам;
- (3) нахождение процентного отношения двух чисел.
Рассмотрим примеры таких задач:
- (1) Надо вспахать поле, площадь которого равна 300 га. В первый день трактористы выполнили 40 % задания. Сколько гектаров они вспахали в первый день?
- (2) В первый день трактористы вспахали 120 га, что составляет 40 % всего поля. Найдите площадь всего поля.
- (3) Надо вспахать поле, площадь которого равна 300 га. В первый день трактористы вспахали 120 га. Сколько процентов всего поля они вспахали в первый день?
Попытайтесь решить каждую из этих задач несколькими способами, заменив 40 % дробью 0,4 или 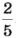
Такие задачи удобно решать способом пропорции. Оформлять решение приведенных выше задач можно так.
Кроме трех основных видов задач, существуют более сложные задачи на проценты. Прежде всего, это задачи, в которых говорится об увеличении или уменьшении чего-либо на несколько процентов, и обратные им. Решая такие задачи, уточняйте, от чего надо брать проценты. Об этом в задаче прямо не сказано, но существуют договоренности о понимании тех или иных высказываний.
Для примера рассмотрим задачу:
Пример №48
Сначала цену на товар подняли на 10%, а потом снизили на 10%. Как изменилась цена на этот товар в результате двух переоценок?
Обратите внимание, что первый раз речь идет о 10% от начальной цены, а во второй раз — о 10% от повышенной цены. А они не равны.
Решение:
Пусть сначала товар стоил 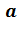
После повышения цены на 10% он стал стоить 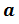
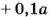
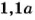
10 % от повышенной цены составляют (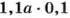
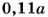
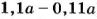
Таким образом, сначала товар стоил 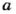
Ответ. После двух переоценок начальная цена товара снизилась на 1 %.
Примечание. Вместо слов «сколько процентов» иногда говорят «какой процент» (см. задачи 700, 701).
Выполнение заданий:
Пример №49
В классе всего 27 учеников, два из них отсутствуют. Сколько процентов составляют отсутствующие? Сколько процентов составляют присутствующие?
Решение:
Ответ.
Примечание. Вторую часть задачи можно решить проще:
Пример №50
Рабочий за смену изготовлял 250 деталей, а теперь изготовляет 270 таких деталей. На сколько процентов повысилась его производительность труда?
Решение:
270 : 250 = 1,08 = 108 %; 108 % — 100 % = 8 %.
270 — 250 = 20 (деталей); 20 : 250 = 0,08 = 8 %.
Пропорциональные величины
Пусть 1 кг яблок стоит 3 грн. Сколько стоят 2 кг, 3 кг, 4 кг, 5 кг, 6 кг таких яблок? Ответ можно записать в виде таблицы.
Масса яблок (кг) 1 2 3 4 5 6 Стоимость (грн.) 3 6 9 12 15 18
Здесь две величины: масса и стоимость. Возьмем какие-либо два значения массы, например 3 кг и 5 кг. Соответствующие им значения стоимости: 9 грн. и 15 грн. Из этих четырех чисел можно составить пропорцию 3:5 = 9: 15 или 3:9 = 5: 15. Такие величины называют пропорциональными. Стоимость яблок пропорциональна их массе. Чем больше покупают яблок, тем больше за них платят. Во столько же раз!
Две величины называют пропорциональными, если с увеличением значений одной из них в несколько раз значения второй увеличиваются во столько же раз.
Другие примеры пропорциональных величин: объем бензина и его масса, время полета самолета и пройденное им расстояние, длина стороны квадрата и его периметр. А вот площадь квадрата не пропорциональна длине его стороны. Почему? Если каждую сторону квадрата увеличить, например, в 3 раза, то его площадь увеличится не в 3 раза, а в 9 раз.
Если величины 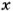
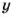
где 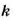
Много задач на пропорциональные величины можно решать с помощью пропорций.
Пример №51
Масса 5 л растительного масла равна 4 кг. Какова масса 12 л этого масла?
Решение:
Первый способ (приведение к единице). Если масса 5 л масла равна 4 кг, то масса 1 л — в 5 раз меньше, то есть 0,8 кг. Масса 12 л масла в 12 раз больше: 0,8 кг — 12 = 9,6 кг.
Второй способ (способ пропорции).
12 л — 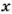
Имеем пропорцию 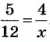
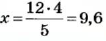
Кроме пропорциональных величин, часто рассматривают обратно пропорциональные величины. Две величины называют обратно пропорциональными, если с увеличением в несколько раз значений одной величины значения другой уменьшаются во столько же раз. Такими, например, являются скорость и время (при постоянном расстоянии). Поскольку, если скорость движения увеличить в несколько раз, то это же расстояние можно пройти во столько же раз быстрее. Если величины 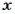
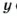
где 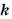
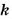
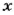
Обратно пропорциональные величины изучают в курсе алгебры. Чтобы различать пропорциональные величины и обратно пропорциональные, первые также называют прямо пропорциональными величинами. Таким образом, пропорциональные величины и прямо пропорциональные величины — одно и то же понятие.
Выполнение заданий:
Пример №52
Насос за 8 ч откачивает 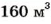
Решение:
Первый способ. За 1 ч насос откачивает 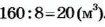
Имеем пропорцию 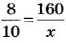
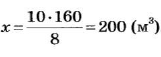
Задачи на пропорциональное деление
Существует много задач, в которых требуется разделить какое-то число или значение величины на части, пропорциональные нескольким данным числам. Рассмотрим одну из таких задач.
Пример №53
Проволоку длиной 60 м разрезали на три части, длины которых пропорциональны числам 2, 3 и 5. Найдите длины этих частей проволоки.
Решение:
Если искомые длины пропорциональны числам 2, 3 и 5, то они равны 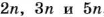
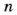
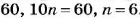
Чтобы понять общее правило решения задач на пропорциональное деление, уравнение 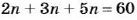
Тогда искомые значения 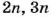
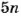
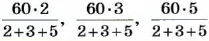
Чтобы разделить число на части, пропорциональные данным числам, надо разделить его на сумму данных чисел и найденное частное умножить на каждое из них.
Отдельным видом задач на пропорциональное деление являются задачи на нахождение двух чисел по их сумме и отношению. Сравните две такие задачи.
Задача 1. Поле площадью 100 га разделили на две части, площади которых пропорциональны числам 2 и 3. Найдите площади этих частей поля.
Задача 2. Поле площадью 100 га разделили на две части, площади которых относятся как 2 : 3. Найдите площади этих частей поля.
Решать такие задачи можно двумя способами.
Решение:
Первый способ. Если площади частей ноля пропорциональны числам 2 и 3 (или относятся как 2 : 3), то они равны 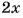
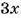
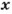
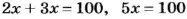
Отсюда 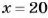
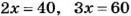
Ответ. 40 га и 60 га.
Второй способ. По правилу деления числа на части, пропорциональные данным числам, сразу определяем площади частей поля:
Ответ. 40 га и 60 га.
Иногда говорят о делении числа на части, обратно пропорциональные данным числам. Поделить число на части, обратно пропорциональные данным числам, — это значит разделить данное число на части пропорционально числам, обратным данным. Например, разделим число 190 на три части, обратно пропорциональные числам 2, 4 и 5. Обратные им числа — 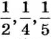
Ответ: 100, 50 и 40.
Выполнение заданий:
Пример №54
Разность двух чисел равна 13, а относятся они как 7 : 5 (рис. 54). Найдите эти числа.
Решение:
По условию задачи искомые числа равны 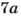
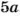
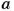
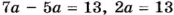
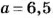
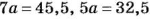
Окружность и круг
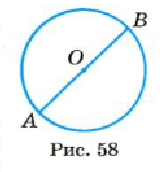
Окружность можно начертить циркулем (рис. 57). Если острие циркуля, каким начерчена окружность, находится в точке О, то эта точка — центр данной окружности. Отрезок, соединяющий любую точку окружности с ее центром, называется радиусом окружности. А отрезок, который соединяет две точки окружности и проходит через ее центр, — диаметром. На рисунке 58 точка О -центр окружности, 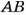
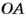
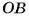
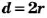
Форму окружности имеет обруч, обод стакана, экватор и параллели на глобусе и т. п. Чтобы измерить длину окружности, можно вдоль нее положить нить, а йотом измерить ее длину. А можно длину окружности не измерять, а вычислять. Ученые еще в древние времена установили, что отношение длины каждой окружности к длине ее диаметра равно одному и тому же числу, приближенное значение которого равно 3,14. Это число во всем мире обозначают буквой 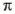
Следовательно, если длина окружности 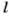
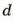
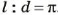
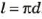
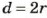
Это — формула длины окружности.
Например, если радиус окружности равен 5 см, то ее длина
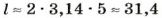
Ответ приближенный, поскольку 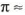
Окружность на плоскости разбивает ее на две области: внутреннюю и внешнюю. Объединение окружности и ее внутренней области называют кругом (рис. 59). Центр, радиус, диаметр круга — это соответственно центр, радиус, диаметр окружности, которая ограничивает данный круг. Площадь круга, как и длина окружности, зависит от длины его радиуса. Доказано, что площадь каждого круга радиуса 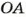
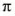
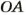
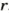
Это — формула площади круга.
Например, если радиус круга равен 10 см, то площадь этого круга
Часть круга, ограниченная его двумя радиусами, называется круговым сектором. На рисунке 61 изображен круг, разделенный на 3 равные сектора. Подумайте, как можно найти площадь каждого из них, если радиус круга равен
Если крут вращать вокруг его диаметра, то образуется шар.
Все точки поверхности шара одинаково удалены от центра шара. Отрезок, соединяющий центр шара с любой точкой его поверхности, называется радиусом шара. Отрезок, который соединяет две точки поверхности шара и проходит через его центр, — диаметром шара. Диаметр шара равен двум его радиусам. Па рисунке 62 изображен шар с центром О и радиусом OA.
Если через центр шара провести плоскость, то она пересечет шар по кругу, а поверхность шара — по окружности. На географическом глобусе такими окружностями являются экватор и линии меридианов. Поскольку длина окружности радиуса 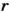
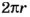
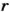
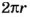
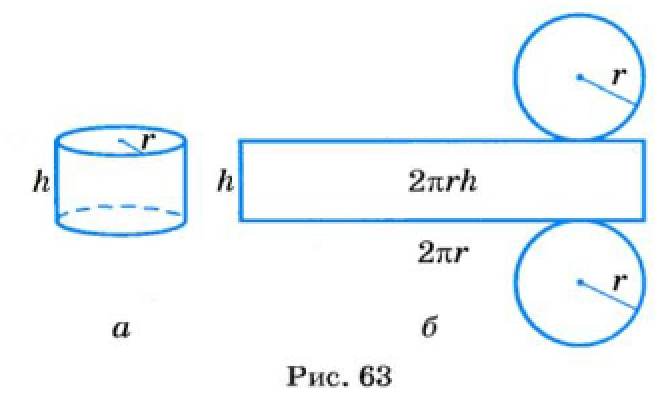
Кругами являются также основания цилиндра (рис. 63, а).
Разрезав поверхность цилиндра вдоль некоторых линий (каких?), ее можно развернуть. В результате образуется развертка поверхности цилиндра (рис. 63, б). Боковая поверхность цилиндра развертывается в прямоугольник. Основание этого прямоугольника равно длине окружности основания цилиндра. Если радиус основания цилиндра равен 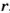
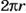
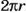
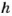
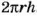
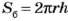
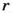
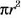
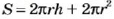
Выполнение заданий:
Пример №55
Какой путь проходит за 1 ч конец часовой стрелки, длина которой равна 30 см (рис. 64)?
Решение:
Длина окружности, описанной концом стрелки, равна
За час стрелка опишет 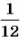
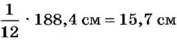
Ответ. 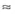
Диаграммы
Рисунки воспринимаются и запоминаются лучше, чем слова и цифры. Для наглядного изображения числовых значений различных величин используют диаграммы. Это слово греческого происхождения, оно обозначает «рисунок». Диаграмма — это символический рисунок, который наглядно иллюстрирует соотношение между значениями величин. Чаще всего используют линейные, столбчатые и круговые диаграммы.
Линейная диаграмма, как правило, состоит из нескольких отрезков. Например, изображенная на рисунке 70 диаграмма позволяет наглядно сравнить длины наибольших рек Европы. Большему значению длины реки соответствует
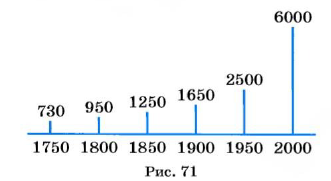
более длинный отрезок. На этой диаграмме отрезки расположены горизонтально. На других диаграммах их изображают вертикально. Линейная диаграмма на рисунке 71 иллюстрирует, как с годами увеличивалось население Земли (в миллионах). В 1750 г. людей было примерно 730 миллионов, в 1800 г. — 950 миллионов и т. д. В 2000 г. было примерно 6 миллиардов человек.
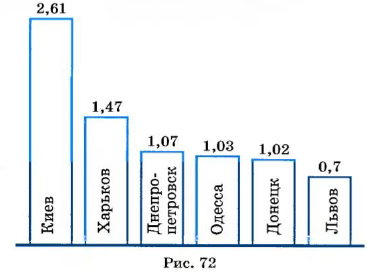
Столбчатая диаграмма отличается от линейной тем, что в ней отрезки заменены прямоугольниками. Такой является диаграмма, изображенная на рисунке 72. На ней
сравнивается численность населения наибольших городов (в миллионах; по данным переписи 2001 г.).
Круговая диаграмма имеет вид круга, разделенного радиусами на части (секторы). Поэтому такие диаграммы называют также секторными. На рисунке 73 изображена диаграмма, которая показывает, сколько процентов живет, русских и людей других национальностей (данные за 2001 г.). Весь круг соответствует 100 процентам.
Иногда диаграмма помогает решить задачу. Пусть, например, надо найти два числа, сумма которых равна 27, а разность — 7. Этой задаче соответствует диаграмма, изображенная на рисунке 74. Первое число больше второго на 7. Если из первого вычесть 7, получим 20 — удвоенное второе число. Таким образом, второе число равно 10, а первое — 17. Так, пользуясь диаграммой, задачу можно решить устно.
Иногда на диаграммах вместо столбиков изображают прямоугольные параллелепипеды или цилиндры (рис. 75). При этом придерживаются таких требований: основания таких фигур должны быть равны, а высоты — пропорциональны соответствующим значениям величин.
Когда хотят изобразить наглядно соотношения между сродными объектами, пользуются кругами, овалами и т. п. Например, соотношения между четырехугольниками, прямоугольниками и квадратами можно изобразить так, как показано на рисунке 76. Такие схематические изображения называют диаграммами Эйлера — в честь известного швейцарского математика Леонарда Эйлера (1707-1783)
Выполнение заданий:
Пример №56
Постройте столбчатую диаграмму, отображающую площади океанов по данным таблицы.
Решение:
Построим на одной прямой равные основания четырех прямоугольников. Пусть площади 10 млн кв. км соответствует прямоугольник, высота которого равна одной клеточке тетради (0,5 см). Высоту столбика, который соответствует площади Тихого океана, найдем из пропорции 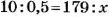
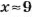
Пример №57
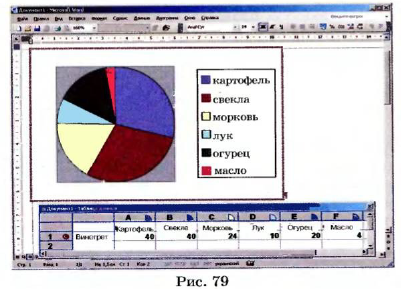
Постройте при помощи компьютера секторную диаграмму, которая отображает состав винегрета (картофель — 40 г, свекла — 40 г, морковь — 24 г, лук — 10 г, огурец квашеный — 20 г, растительное масло — 4 г).
Решение:
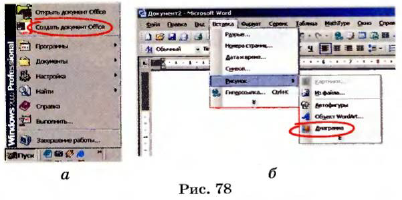
1. Включите компьютер, при помощи кнопки «Пуск» создайте новый документ (рис. 78, а).
2. В открытом окне последовательно нажмите кнопки «Вставка» 

3. В новом окне нажмите последовательно кнопки «Диаграмма» 
4. Введите в таблицу заданные значения (рис. 79).
5. Сохраните и распечатайте полученное изображение. Оно может быть таким, как на рисунке 79.
Отношения чисел интересовали ученых Египта и Вавилона еще 4000 лет назад. Математики Древней Греции исследовали в основном отношения отрезков. А поскольку длины отрезков выражаются числами, то все их знания об отношении отрезков верны и для отношения чисел.
Пропорции также были хорошо известны египтянам, вавилонянам и грекам. В знаменитом труде «Начала» Евклида (IV в. до н. э.) им посвящена вся пятая книга. В частности, в ней обосновано и много «производных пропорций», которые вытекают из какой-то данной.
Самой прекрасной пропорцией древние греки считали «золотую пропорцию», когда отрезок длиной 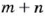
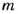
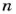
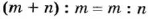
Окружность и круг людям были известны еще в древние времена. Раньше люди не различали окружность и круг.
В наших краях еще несколько тысячелетий назад женщины носили украшения, которые имели детали в виде окружностей (рис. 84). И колеса колесниц мастеровые люди умели изготовлять еще несколько тысячелетий до новой эры.
Изобретение колеса — большое открытие. Сначала люди пользовались катками, потом, чтобы катки не переносить, додумались вставлять их в прорезы, словно в подшипники. Со временем колеса начали изготовлять отдельно от оси, но из сплошного дерева. Только позже научились изготовлять колеса со спицами, которые были больше, легче и крепче. Схематически историю изобретения колеса показано на рисунке 85.
Интересная история числа 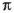
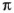
Древнегреческий ученый Архимед нашел, что 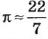
Главное в разделе:
Частное от деления двух чисел называют также их отношением. Отношение чисел 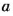
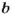
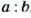
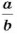
Основное свойство отношения. Значение отношения не изменится, если оба члена умножить или разделить на одно и то же число, отличное от нуля. Например, 300 : 500 = 3:5.
Отношение дробных чисел всегда можно заменить отношением натуральных чисел. Например,
Процентным отношением называют отношение, выраженное в процентах. Например, 3:15 = 0,2 = 20 %.
Вероятностью события называют отношение количества благоприятных для него результатов к количеству всех возможных результатов. Например, вероятность того, что подброшенная монета упадет кверху гербом, равна 0,5.
Отношение длины каждой окружности к ее диаметру равно числу 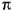
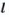
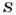
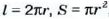
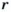
Равенство двух oiношений называют пропорцией.
Примеры:
пропорций:
Основное свойство пропорции. Если пропорция верна, то произведение ее крайних членов равно произведению средних. То есть, если
Две величины называют пропорциональными (прямо пропорциональными), если с увеличением значений одной из них в несколько раз значения другой увеличиваются во столько же раз. Например, стоимость товара пропорциональна его количеству, пройденный автомобилем путь (при равномерном движении) пропорциональный времени движения. Если величины 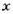
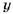
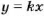
Чтобы разделить число на части, пропорциональные данным числам, надо разделить его на сумму данных чисел и умножить на каждое из них. Разделим, например, число 540 на три части, пропорциональные числам 2, 3 и 5.
Умножив 54 на 2, на 3 и на 5, имеем: 108, 162 и 270.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Рациональные числа и действия над ними
- Делимость натуральных чисел
- Выражения и уравнения
- Линейное уравнение с одной переменной
- Криволинейные интегралы
- Двойные и тройные интегралы
- Делимость чисел в математике
- Обыкновенные дроби
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Длина окружности. Площадь круга, 6 классСкачать

Длина окружности
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.
Определение длины окружности
Видео:+Как найти длину окружностиСкачать

Формула расчёта длинны окружности
Произвести расчёт окружности можно по следующей формуле:
r – радиус окружности
D – диаметр окружности
L – длина окружности
Видео:Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

Пример нахождения длинны окружности
Вычислить длину окружности, имеющей радиус 10 сантиметров.
Формула для вычисления дины окружности имеет вид:
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Длина окружности и площадь круга. Урок в 6-м классе
Разделы: Математика
Класс: 6
Ключевые слова: площадь круга
Цель урока: формирование и развитие у учащихся личностных; регулятивных; познавательных и коммуникативных способов действия; вывести формулы длины окружности и площадь круга и показать ее применение при решении задач.
Задачи урока:
Образовательные:
- изучить формулы длины окружности и площади круга;
- показать применение этих формул при решении задач;
- познакомить учащихся с постоянной величиной π;
- отработать навыки проведения эксперимента и с помощью экспериментальных данных делать выводы.
Развивающие:
- развивать познавательный интерес учащихся в процессе ознакомления с историческим материалом;
- развивать навыки устного счёта;
- развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к «видению» проблемы;
- формировать умения чётко и ясно излагать свои мысли;
- развивать пространственное воображение учащихся.
Воспитательные:
- прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности;
- воспитывать умение работать с имеющейся информацией в необычной ситуации;
- воспитывать уважение к математике, умение видеть математические задачи в окружающем нас мире.
Тип урока: урок изучения нового материала.
Форма работы: индивидуальная, работа в парах, коллективная.
Оборудование: раздаточный материал; для практической работы: нитки, ножницы, циркуль, линейка, карандаш.
1. Практическая работа по теме «Длина окружности и площадь круга». 6 класс
Цель: Проверить знания формул вычисления длины окружности и площади круга.
Пособие: круг с ниткой.
Задания:
- Найти длину окружности, практическим путем (с помощью нитки)
- Измерить линейкой диаметр окружности. Найти длину окружности по формуле.
- Найти радиус окружности. Найти площадь круга.
Оформление работы:
1) Длина нитки = длина окружности =
Оформление работы:
1) Длина нитки = длина окружности =
Историческое сообщение о числе π
Символ π означает отношение длины окружности к ее диаметру. Впервые в этом смысле символ π был использован У.Джонсом в 1707, а Л.Эйлер, приняв это обозначение, ввел его в научный обиход. Еще в древности математикам было известно, что вычисление значения π и площади круга — задачи, тесно связанные между собой. Древние китайцы и древние евреи считали число π равным 3. Значение числа π, равное 3,1605, содержится в древнеегипетском папирусе писца Ахмеса (около 1650 до нашей эры). Около 225 до нашей эры Архимед, используя вписанный и описанный правильные 96-угольники, приближенно вычислил площадь круга с помощью метода, который привел к значению ПИ, заключенному между 31/7 и 310/71. Другое приближенное значение π, эквивалентное обычному десятичному представлению этого числа 3,1416, известно что ван Цейлен (1540-1610) вычислил значение ПИ с 32 десятичными знаками
π =3,141592653589793238462643…(24 знака)
Вычисление как можно большего числа точных цифр числа с помощью компьютера занимает математиков и в настоящее время. Так, в 1988 году, японский ученый Ясума Канеда вычислил 400 млн точных цифр после запятой. Это не только спортивный интерес, необходимо и для изучения случайных процессов. В школьном же курсе математики π =3,14.
День числа π (пи) отмечается любителями математики 14 марта в 1:59:26.
Этот неофициальный праздник придумал в 1987 году физик из Сан-Франциско Ларри Шоу, который подметил, что в американской системе записи дат (месяц / число) дата 14 марта — 3/14 — и время 1:59:26 совпадает с первыми разрядами числа π = 3,1415926….
В это время читают хвалебные речи в честь числа π, его роли в жизни человечества, рисуют антиутопические картины мира без π, пекут и едят «пирог» с изображением греческой буквы «пи» или с первыми цифрами самого числа, пьют напитки и играют в игры, начинающиеся на «пи», решают математические головоломки и загадки, водят хороводы вокруг предметов, связанных с этим числом.
2. Практические задачи
1.Найти радиус колеса, у которого длина окружности 125,6 см.
Решение: R= 125,6:( 2*3,14)=20 см.
2. Найти длину окружности круглой комнаты, если диаметр её D = 5,5 м.
Решение: С=5,5*3,14=17,27 см
Ход урока
1. Организационный момент (1-2 минуты)
Я рада вас всех видеть. Чтобы начать работу, проверим, всё ли готово к уроку.
2. Постановка цели и мотивация (3-5 минут)
Тема нашего урока — Длина окружности и площадь круга. Запишем ее в тетрадь.
Ребята, давайте перед практической работой сделаем разминку. Сядьте ровно.
Покажите мне руками маленькую окружность. А теперь представьте, что наша окружность раздувается, становится все больше и больше. Показываем, вот какая получилась окружность. А теперь поднимаем эту окружность над собой и держим над головой. Представим, что подул ветер и наша окружность наклоняется сначала влево, потом вправо. А теперь представим, что окружность превратилась в воздушный шарик и отпускаем ее.
Молодцы! Приступаем к работе!
Практическая работа №1 (15 минут)
Учащиеся выполняют практические задания по команде учителя и записывают свои наблюдения (учитель может все проделывать на доске, если класс не достаточно подготовлен к самостоятельной работе, или предложить ученикам работать в парах).
- На картонном листе начертить окружность с произвольным радиусом, отметить её центр, записать значение радиуса в миллиметрах(r) и значение диаметра в миллиметрах (d).
- Провести клеем-карандашом по окружности и, пока клей не высох, проложить нитку точно по контуру окружности и аккуратно отрезать её на стыке.
- Снять нитку с картона и очень точно измерить её длину в миллиметрах. Этот размер назовем длиной окружности (C). Записать значение C.
- Найти отношение C/d с помощью калькулятора, округлить получившуюся дробь до тысячных, до сотых, до десятых, до целых. Сделать соответственные записи.
Если бы мы, ребята, еще более точно измерили длину окружности, ее диаметр и более точно выполнили вычисления длины окружности к ее диаметру, то получили бы число 3,14…. Это число математики обозначают буквой π (пи).
Индивидуальная работа. Каждый работает самостоятельно, используя указания учителя, делают соответственные записи в тетради.
C/d = 195 : 60 = 3,25
C/d = 292 : 90 = 3, 2444)
Далее ученики называют свои результаты и замечают, что, хотя окружности были построены у всех разные, отношения длины к диаметру получились примерно одинаковые отношения больше 3, но меньше 4. Значит, можно записать:
Так как прямоугольник был составлен из частей круга, то их площади равны. Значит, площадь круга равна: S = πR 2 .
Другой способ вывода формулы площади круга вы найдете в учебнике.
Необходимо распределить слова на две группы «Окружность» и «Круг».
На доске, стенах класса с помощью магнитов и скотча прикреплены слова, ученики одновременно по команде учителя распределяют слова по группам. Время выполнения ограниченно.
(Плоская тарелка, блин, пяльцы для вышивания, резинка для волос, компакт-диск, покрышка для колес, обруч (халахуп), кольцо, бублик, колечко колбасы).
📽️ Видео
Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Окружность и круг, 6 классСкачать

КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Длина окружности. 9 класс.Скачать

КАК НАЙТИ ДЛИНУ ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР ИЛИ РАДИУС? Примеры | МАТЕМАТИКА 6 классСкачать

Геометрия 9 класс (Урок№23 - Длина окружности.)Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Площадь круга. Математика 6 класс.Скачать

8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

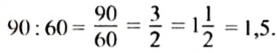
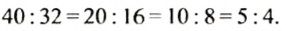
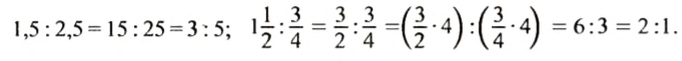
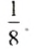
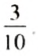
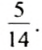
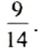

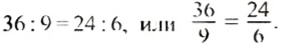
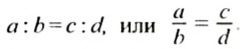
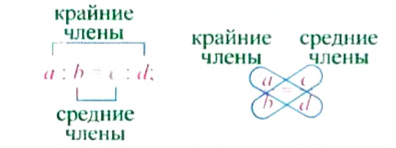
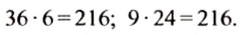
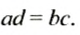
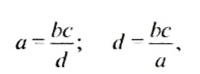
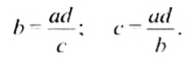
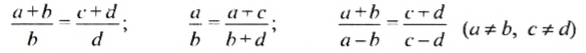
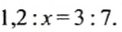
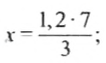
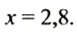
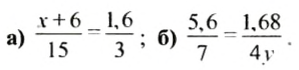
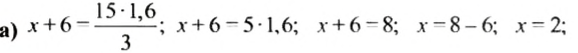
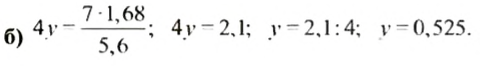
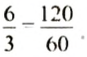
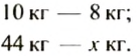
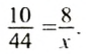
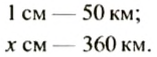
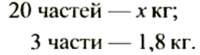
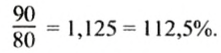
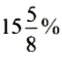
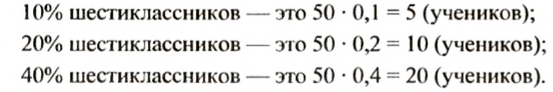
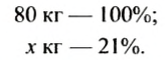
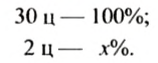
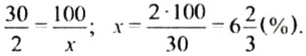
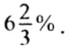
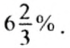
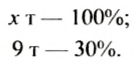
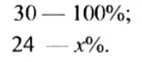
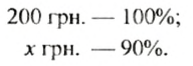
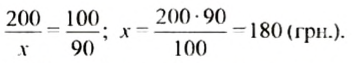
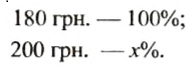
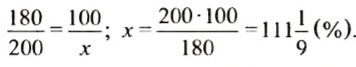
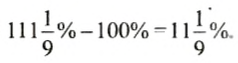
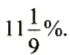
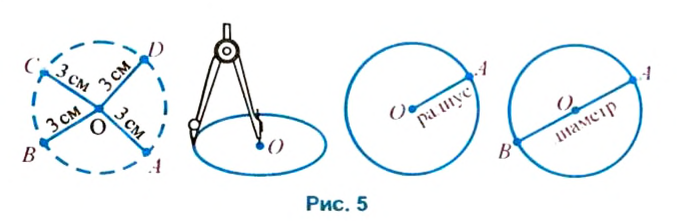
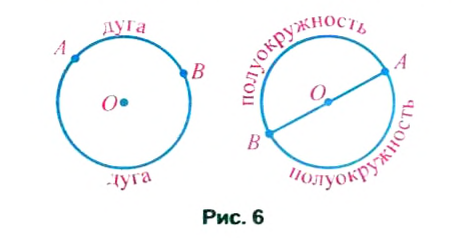
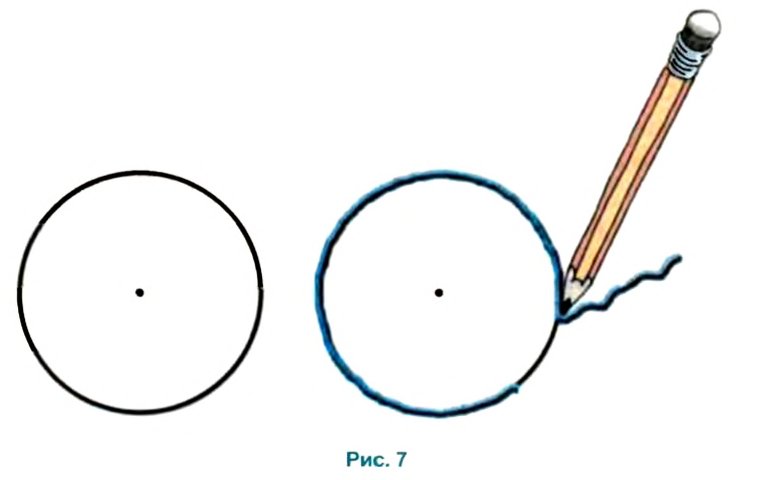

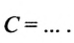
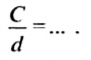
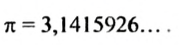
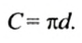
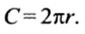
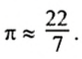
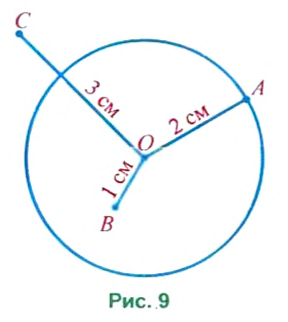
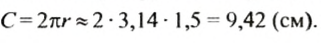
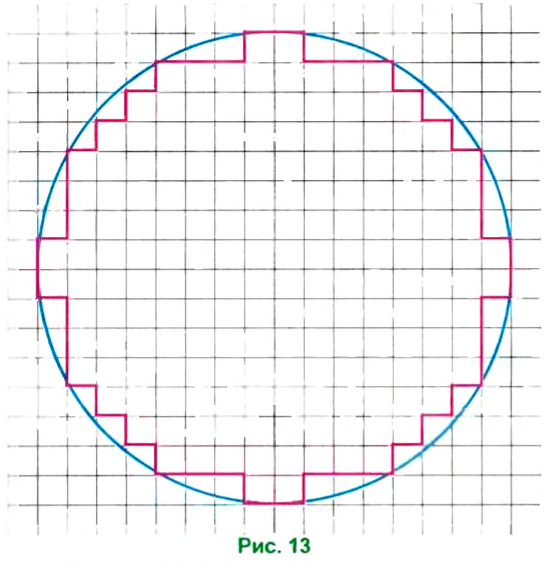
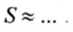
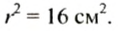
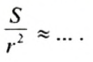
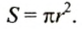
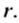
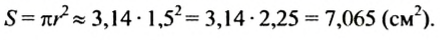
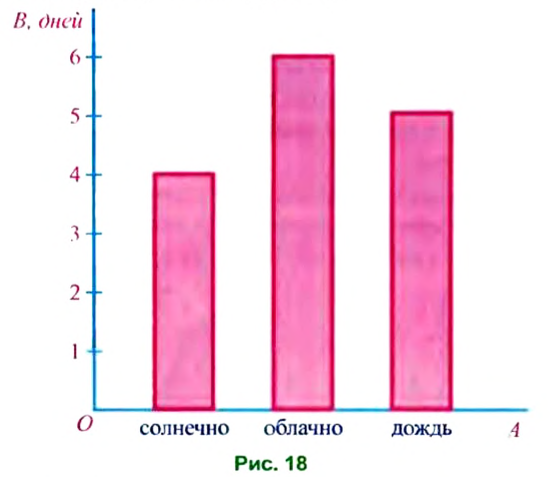
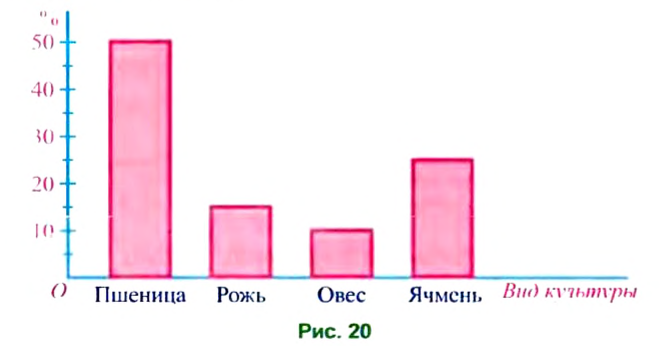
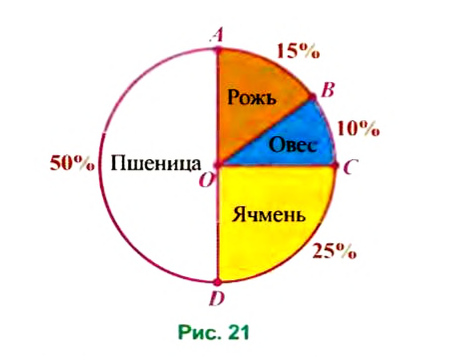
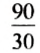 — отношение;
— отношение; 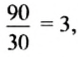 число 90 в три раза больше от числа 30.
число 90 в три раза больше от числа 30. 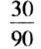 — отношение;
— отношение; 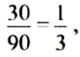 число 30 составляет
число 30 составляет 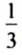 от числа 90.
от числа 90.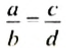 — пропорция.
— пропорция.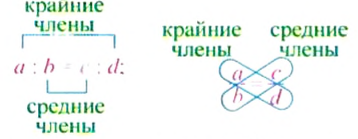
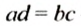 — основное свойство пропорции.
— основное свойство пропорции.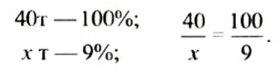
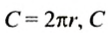 — длина окружности,
— длина окружности, 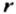 — ее радиус,
— ее радиус, 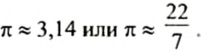
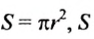 — площадь круга,
— площадь круга, 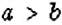 , то значение отношения
, то значение отношения 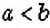 , то значение отношения
, то значение отношения 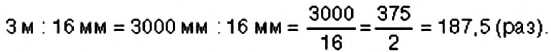
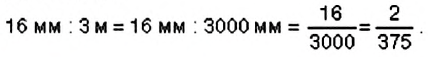
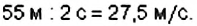
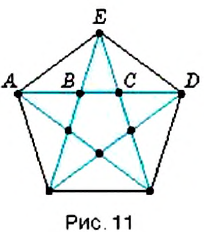
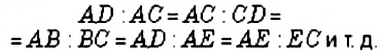
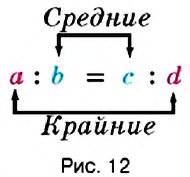


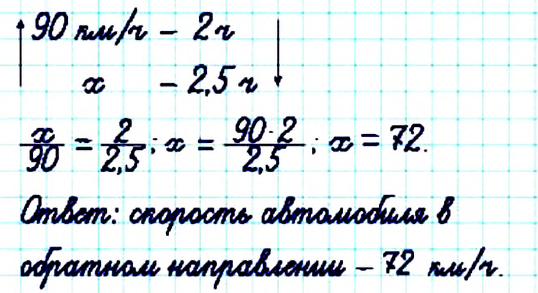

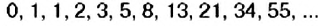
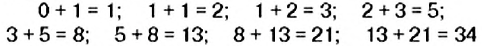
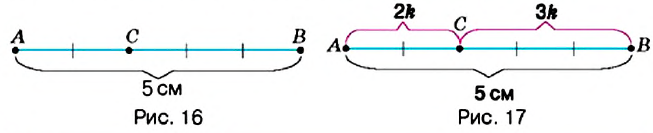
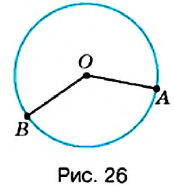
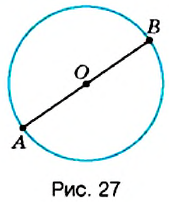
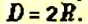
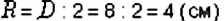

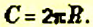

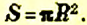
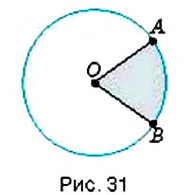
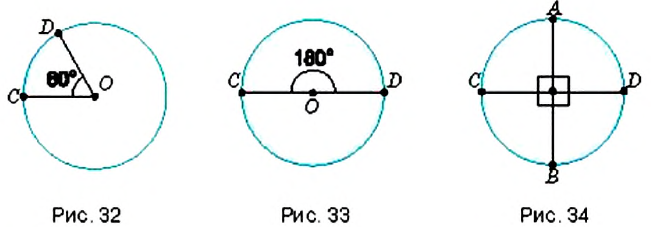
 .
.