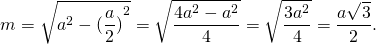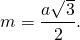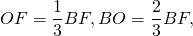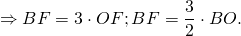Как находить медиану равностороннего треугольника

В данной статье мы рассмотрим определение и свойства медианы равностороннего треугольника, а также разберем примеры решения задач для закрепления изложенного материала.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Определение медианы

Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны.

Треугольник называется равносторонним, если все его стороны равны (AB = BC = AC).

Видео:НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

Свойства медианы равностороннего треугольника

Свойство 1

Любая медиана в равностороннем треугольнике одновременно является и высотой, и серединным перпендикуляром, и биссектрисой угла, из которого проведена.

BD – медиана, высота и серединный перпендикуляр к стороне AC, а также биссектриса угла ABC;

Свойство 2

Все три медианы в равностороннем треугольнике равны между собой. Т.е. AF = BD = CE.

Свойство 3

Медианы в равностороннем треугольнике пресекаются в одной точке, которая делит их в отношении 2:1.

Свойство 4

Любая медиана равностороннего треугольника делит его на два равных по площади (равновеликих) прямоугольных треугольника. Т.е. S₁ = S₂.

Свойство 5

Равносторонний треугольник делится тремя медианами на шесть равновеликих прямоугольных треугольников. Т.е. S₁ = S₂ = S₃ = S₄ = S₅ = S₆.

Свойство 6

Точка пересечения медиан в равностороннем треугольнике является центром описанной вокруг и вписанной окружностей.

• r – радиус вписанной окружности;
• R – радиус описанной окружности;
• R = 2r (следует из Свойства 3).

Свойство 7

Длину медианы равностороннего треугольника можно вычислить по формуле:

a – сторона треугольника.

Видео:Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

Примеры задач

Задача 1
Вычислите длину медианы равностороннего треугольника, если известно, что его сторона равна 6 см.

Решение
Для нахождения требуемого значения применим формулу выше:

Задача 2
Самая большая сторона одного из треугольников, образованных в результате пересечения трех медиан в равностороннем треугольнике, равняется 8 см. Найдите длину стороны данного треугольника.

Решение
Нарисуем чертеж согласно условиям задачи.

Из Свойства 5 мы знаем, что в результате пересечения всех медиан образуются 6 прямоугольных треугольников.

• BG = 8 см (самая большая сторона, является гипотенузой △BFG);
• FG = 4 см (катет △BFG, в 2 раза меньше гипотенузы BG – следует из Свойства 3).

Применяем теорему Пифагора, чтобы найти длину второго катета BF:
BF 2 = BG 2 – FG 2 = 8 2 – 4 2 = 48 см 2 .
Следовательно, BF ≈ 6,93 см.

BF равняется половине стороны BC (т.к. медиана делит сторону треугольника пополам), следовательно, BC ≈ 13,86 см.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Медиана равностороннего треугольника

Какими свойствами обладает медиана равностороннего треугольника? Как выразить длину медианы через сторону треугольника? Через радиус вписанной и описанной окружностей?

(свойство медианы равностороннего треугольника)

В равностороннем треугольнике медиана, проведённая к любой стороне, является также его биссектрисой и высотой.

Пусть в треугольнике ABC AB=BC=AC.

Проведём медиану BF.

Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.

По свойству медианы равнобедренного треугольника, BF является также его биссектрисой и высотой.

Аналогично, так как AB=AC, треугольник ABC — равнобедренный с основанием BC, AK — его медиана, биссектриса и высота;

так как AC=BC, треугольник ABC — равнобедренный с основанием AB, CD — его медиана, биссектриса и высота.

Что и требовалось доказать .

(свойство медиан равностороннего треугольника)

Все три медианы равностороннего треугольника равны между собой.

Пусть в треугольнике ABC AB=BC=AC,

AK, BF, CD — его медианы.

Следовательно, треугольники ABK, BCF и CAK равны (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон:

Что и требовалось доказать .

Из 1 и 2 теоремы следует, что все медианы, биссектрисы и высоты равностороннего треугольника равны между собой.

1) Выразим длину медианы равностороннего треугольника через его сторону.

Так как медиана равностороннего треугольника является также его высотой, треугольник ABF- прямоугольный.

Обозначим AB=a, BF=m, тогда AF=a/2.

Таким образом, формула медианы равностороннего треугольника по его стороне:

2) Выразим медиану равностороннего треугольника через радиусы вписанной и описанной окружностей.

Центр правильного треугольника является центром его вписанной и описанной окружностей.

Так как центр вписанной окружности лежит в точке пересечения биссектрис треугольника, а медианы равностороннего треугольника являются также его биссектрисами, в равностороннем треугольнике ABC OF — радиус вписанной, BO — радиус описанной окружностей:

Так как медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то BO:OF=2:1. Таким образом,

Отсюда медиана равностороннего треугольника через радиус вписанной окружности равна

Видео:Задача найти сторону равностороннего треугольника по медианеСкачать

Медиана равностороннего треугольника

Средняя оценка: 4.6

Всего получено оценок: 93.

Средняя оценка: 4.6

Всего получено оценок: 93.

Равносторонний треугольник стоит особняком среди всех фигур: в нем легко можно найти значение всех сторон и углов, так как все углы известны заранее, а найдя одну сторону, можно найти сразу все три. Но именно из-за этих свойств, составители задач любят писать каверзные условия, в которых не всегда можно разобраться с первого раза, например, не всегда можно понять, что такое медиана, потому что человеку проще воспринимать понятие высоты, нежели медианы. Рассмотрим же понятие медианы в равностороннем треугольнике подробно.

Видео:Теорема о свойстве медианы равнобедренного треугольникаСкачать

Определения

Равносторонний треугольник – это треугольник, все стороны которого равны, а углы по 60 градусов.

Равносторонний треугольник это частный случай равнобедренного, но в равностороннем любую сторону можно считать основанием.

Из этого следует, что любая высота равностороннего треугольника является медианой и биссектрисой, так как любая высота проводится к стороне, которую можно считать основанием.

Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположно стороны. Медиана также имеет ряд свойств, которые можно использовать в решении задач.

Медианы в треугольнике пересекаются в одной точке и делят эту точку в отношении 2:3, считая от вершины. При этом медианы разбивают треугольник на 6 разновеликих треугольников. Если посмотреть на рисунок, то можно увидеть, что в равностороннем треугольнике каждый из 6 этих треугольников будет прямоугольным.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Формула медианы равностороннего треугольника

Выведем формулу медианы равностороннего треугольника. В равностороннем треугольнике АВС проведем высоту АН. Она же будет являться медианой и высотой. Медиана разобьет треугольник на два прямоугольных: АНС и АНВ. Рассмотрим треугольник АНС.

Рис. 2. Рисунок к задаче.

В нем применим теорему Пифагора:

Каждую из сторон обозначим буквой а. Тогда АВ=а; $$ВН=$$

Это и есть формула медианы равностороннего треугольника. С другой стороны, можно воспользоваться тригонометрическими тождествами и вывести еще одну формулу:

При этом угол АСН равен 60 градусам. Значит, можно определить синус угла: $$sin(ACH)=<sqrtover 2>$$

Выразим значение медианы АН

Вот еще одна формула, характерная для равностороннего треугольника.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Задача

Для закрепления темы решим простую задачу на обратное использование формулы медианы.

В равностороннем треугольнике медиана равна $$20over<sqrt>$$. Найти площадь треугольника.

Для нахождения площади воспользуемся классической формулой.

Классическую формулу можно использовать для нахождения площади любого треугольника.

Для нее нам нужно значение стороны и высоты. Высота в равностороннем треугольнике совпадает с медианой, поэтому нужно найти только сторону. Выразим ее через формулу медианы равностороннего треугольника.

Рис. 3. Рисунок к задаче.

Подставим в формулу значение медианы:

Видео:ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

Что мы узнали?

Мы вывели две формулы медианы равностороннего треугольника, дали определения, необходимые для решения задач и решили небольшую задачу для закрепления знаний.

💡 Видео

Задание 9 ОГЭ от ФИПИСкачать

Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

ОГЭ ЗАДАНИЕ 16 РАЗДЕЛ ГЕОМЕТРИЯ ДАН РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК И ВЫСОТА / НАЙТИ МЕДИАНУСкачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать

ОГЭ 16🔴Скачать

Сможешь найти основание? Задача про медиану равнобедренного треугольникаСкачать

Построение медианы в треугольникеСкачать

Геометрия Найдите высоту равностороннего треугольника со стороной aСкачать

Площадь равностороннего треугольникаСкачать