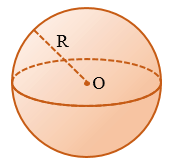
Как начертить шар по радиусу окружности (2 видео)

Содержание

Геометрические фигуры. Шар, сфера.
Развертка (выкройка) сферы
Развертка сферы
Окружность, круг, шар
Основные характеристики окружности
Построение окружности
Шар и сфера
Определение
🎬 Видео

Видео:Радиус и диаметрСкачать

Геометрические фигуры. Шар, сфера.

Шаровой ( сферической ) – другими словами границей шара – поверхностью является геометрическое место точек (т.е. множество всех точек) в пространстве, которые равноудалены от одной точки O , называющейся центром сферической поверхности .

Понятие шара в метрическом пространстве естественным образом обобщает понятие шара в евклидовой геометрии.

Т.о., точками сферы оказывается каждая точка шара, которая удалена от центра на расстояние, которое равно радиусу. Каждый отрезок, который соединяет центр шара и точку на шаровой поверхности, тоже называют радиусом .

Отрезок, который соединяет 2 точки шаровой поверхности и который проходит сквозь центр шара, называется диаметр . Любой диаметр соответствует 2-м радиусам. Концы всякого диаметра называются диаметрально противоположными точками шара.

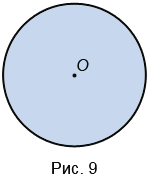
Эта точка О называется центром сферы , а расстояние AO , в свою очередь, называется радиусом сферы .

Радиус AO и диаметр AB находят тем же способом, что и для окружности.

Сфера является поверхностью (границей) шара с центром и радиусом, как у сферы.

Шар — это тело правильно геометрической формы, ограниченное поверхностью шара. Шар возможно получить, методом вращения полукруга/круга около диаметра.

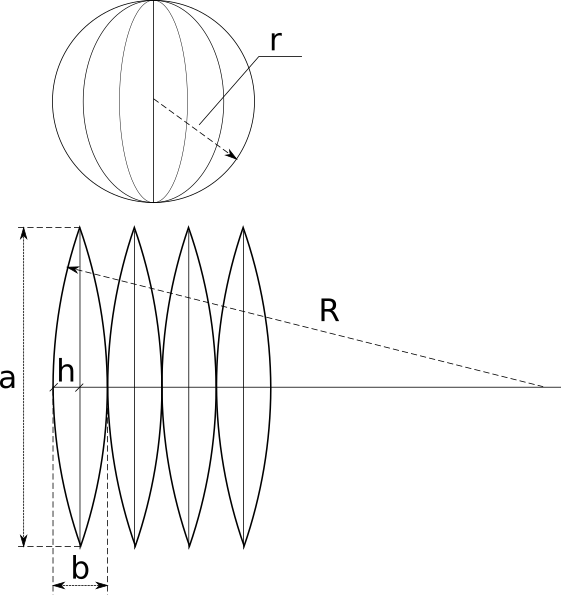
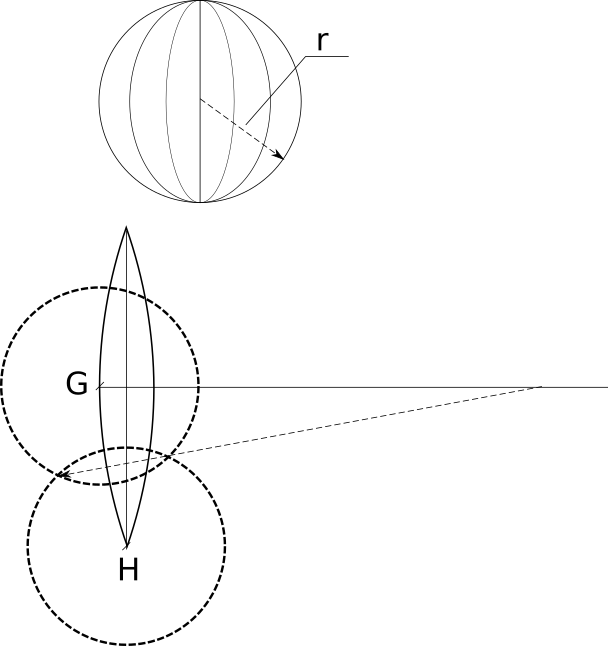
Любое плоское сечение шара является кругом. Чем ближе секущая плоскость к центру шара, тем радиус круга становится больше. Самый большой круг оказывается при прохождении плоскости через центр O. Этот круг разделяет шар на две равные части и он называется большим кругом. Радиус большого круга равен радиусу шара.

Меридианы шара (сферы).

Сквозь 2 точки шара, которые лежат на концах общего диаметра, возможно провести бесконечное число больших кругов — меридианов. Через 2 точки, которые не на концах общего диаметра шара возможно провести всего лишь 1 большой круг.

Основные геометрические формулы шара (сферы).

Площадь поверхности S и объём V шара радиуса r, диаметра d можно определить по формулам:

Определения, связанные с понятием шара.

Предположим, дано метрическое пространство (X, ρ). Значит:

Шаром (или открытым шаром) с центром в точке и радиусом r>0 будет называться

Замкнутый шар с центром в x₀ и радиусом r можно выразить так:

Свойства шара.

Шар – это открытое множеством в топологии, порождённой метрикой ρ.

Замкнутый шар — замкнутое множество в топологии, порождённой метрикой ρ.

По определению этой топологии открытые шары с центрами в любой точке X представляют собой её базу.
Т.е., . Но замыкание открытого шара не всегда совпадает с замкнутым шаром:
Например: допустим (X, ρ) — дискретное метрическое пространство, и X состоит из более, чем 2-х точек. Значит, для всякого будет:

Объём шара в 1,5 раз меньше, чем объём описанного вокруг этого шара цилиндра, а поверхность шара в 1,5 раз меньше полной поверхности этого цилиндра:

S_цил и V_цил – полная поверхность и объём описанного цилиндра вокруг шара.

Части шара.

Часть шара (сферы), которая отсекается от него любой плоскостью (ABC), является шаровым (сферическим) сегментом . Круг ABC является основанием шарового сегмента. О трезок MN перпендикуляра, который проведен из центра N круга ABC до пересечения со сферической поверхностью, является высотой шарового сегмента. Точка M является вершиной шарового сегмента.

Часть сферы, которая заключена между 2-мя плоскостями, которые параллельны ABC и DEF, которые пересекают сферическую поверхность, является шаровым слоем . Кривая поверхность шарового слоя является шаровым поясом . Круги ABC и DEF – основания шарового пояса . Расстояние NK между основаниями шарового пояса – его высота . Часть шара, которая ограничена кривой поверхностью сферического сегмента (AMCB) и конической поверхностью OABC , основанием у нее является основание сегмента (ABC) , а вершиной – центр шара O , называется шаровым сектором.

Формулу объёма шара можно объяснить следующими рассуждениями. В шаре возможно разместить огромное количество пирамид с очень маленькими основаниями, разместив пирамиды таким образом, чтобы их вершины располагались в центре шара, а основания лежали бы на поверхности шара и эти пирамиды соприкасались бы боковыми гранями.

Высота любой построенной пирамиды приблизительно равна радиусу (R) шара. Если не обращать внимание различиями этих длин, то объём (v) всех пирамид отдельно можно представить такой формулой:

Значит, сумма объёмов (V’) пирамид выразим формулой:

Сумма (S’) очень близка к площади поверхности шара (S).

Сумма объёмов всех пирамид (V’) приблизительно равна объёму (V) шара. Если не обращать внимание на незначительные различия в этих величинах, тогда получится такая формула:

которая показывает, что объём шара соответствует 1/3 произведения площади поверхности шара на длину радиуса. Зачастую озвучивают так: объём шара равен 1/3 произведения поверхности шара на его радиус.

Используя выражение S = 4πR 2 , вывели формулу:

где D — диаметр шара.

Примечание. В формуле V = 1/3 SR поставлен знак точного, а не приближённого равенства, хотя на основании проведённых рассуждений можно было принять его приближённым, хотя в старших классах средней школы доказываем, что равенство V = 1/3 SR точное, а не приближённое.

Видео:Длина окружности. Математика 6 класс.Скачать

Развертка (выкройка) сферы

Развертка сферы на плоскость. Калькулятор вычисляет основные параметры развертки, а также выводит координаты точек для построения развертки одной доли.

Калькулятор рассчитывает параметры развертки сферы на плоскости. Картинка ниже иллюстрирует задачу.

Итак, нам известен радиус сферы r и число долей на которое мы хотим ее разбить n. Для описания развертки нам надо найти высоту «дольки» a, ширину «дольки» b, и радиус R большой дуги, на которой построена «долька». Формулы расчета и объяснения, как обычно, приведены под калькулятором.

Развертка сферы

С высотой все понятно — это половина длины окружности, которую можно получить при сечении сферы плоскостью, проходящей через центр. Таким образом,
.
С шириной тоже все понятно — это часть той же окружности, полученная при разбиении всей окружности на n частей:

Радиус дуги можно вычислить по длине хорды (это а) и высоте сегмента (это h=b/2) по следующей формуле (см. Сегмент круга).

В принципе, найдя a и b, считать радиус R даже не обязательно — его можно найти по построению, что иллюстрирует следующая картинка.

Для нахождения радиуса из точек G и H надо провести две окружности, так, чтобы они пересекались — прямая, проведенная через точки пересечения, пересечет среднюю линию в точке центра окружности, на дуге которой лежат G и H.

Несмотря на всю простоту, у метода есть один недостаток — а именно, ему нужно очень много места сбоку для радиуса, и чем больше число долек, на которое мы хотим разбить сферу, тем больше радиус большой дуги. Не везде будет возможность найти столько места и такой большой «циркуль», чтобы нарисовать дугу. Поэтому калькулятор, кроме расчета параметров «дольки», также рассчитывает координаты точек, лежащих на дуге — можно строить дуги дольки по точкам, не используя радиус. Для того, чтобы рассчитать координаты точек, надо пометить флажок «Сгенерировать точки развертки», и указать число точек — дуга будет разбита на заданное число точек с равным угловым шагом, как показано на рисунке:

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Окружность, круг, шар

Окружность — это замкнутая кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки. Заданная точка является центром окружности. На Рис.1 точка О — центр окружности.

Видео:РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

Основные характеристики окружности

1. Радиус — это отрезок, соединяющий центр с какой-либо точкой окружности. У любой окружности можно провести бесконечно много радиусов, которые будут иметь одну и ту же длину. Обозначают радиус r или R. На Рис.2 представлена окружность с центром в точке О радиусом ОА.

2. Хорда — это отрезок, соединяющий две точки окружности. У любой окружности можно провести бесконечно много хорд. На Рис.3 ВС и KD — хорды окружности с центром в точке О.

3. Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр (т.е. диаметр — это частный случай хорды). У любой окружности можно провести бесконечно много диаметров, которые будут иметь одну и ту же длину. На Рис.4 МN — диаметр окружности с центром в точке О. Обозначают диаметр d или D. Диаметр в два раза больше радиуса, т.е. d = 2r (D = 2R), откуда r = d : 2 (R = D : 2), следовательно, центр окружности (точка О) является серединой диаметра.

4. Дуга — это часть окружности, ограниченная двумя точками. На Рис.5 KDC и KBC — дуги, ограниченные точками К и С.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Построение окружности

Для того, чтобы построить окружность используют специальный прибор, который называется циркулем (Рис.6). Циркуль состоит из двух частей, соединённых шарниром. Обычно на конце одной из них располагается игла, на конце другой — пишущий предмет, например грифель карандаша.

Выполнение построения:

отмечаем точку, которая будет центром окружности;
делаем нужный раствор циркуля (расстояние между иглой и грифелем карандаша), т.е. определяем радиус окружности, которую нам нужно построить (Рис.7);

ставим иглу циркуля в точку, которая определяет центр окружности;
проводим окружность данного радиуса (Рис.8).

Часть плоскости, которая лежит внутри окружности (вместе с самой окружностью), называют кругом (Рис.9).

Шар и сфера

Сфера — поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Центр сферы — данная точка (точка О на рисунке выше).

Радиус сферы — данное расстояние (R на рисунке выше), также это любой отрезок, соединяющий центр сферы с какой-либо ее точкой.

Диаметр сферы — отрезок, соединяющий две точки сферы и проходящий через ее центр. Диаметр сферы в два раза больше ее радиуса, т.е. если радиус сферы — R, то ее диаметр — 2R.